矿产资源开发过程中利益相关者利益分配博弈——基于矿山企业、矿区居民、地方政府三方主体的分析

朱 晓，葛书婷

（新疆财经大学，新疆 乌鲁木齐 830012）

一、引言

矿产资源归国家所有，矿产资源开发收益分配的利益相关者包括矿山企业、矿区居民、地方政府。其中，地方政府受中央政府的委托，参与矿产资源开发利益分配的博弈与管理，成为了利益分配的相关者。周丹和熊华丹［1］研究指出，地方政府在矿产资源开发管理中往往会为了追求短期的经济发展而忽略土地恢复和补偿成本。矿山企业在矿产资源开发过程中不断投入生产要素，通过生产经营管理获得相应的收益，自然属于矿产资源开发利益分配的相关者。张炎治等［2］研究发现矿产资源开发企业在获得超额利润的同时，也承担着过重的税负。矿区居民历代生活在矿产资源开发地，土地是其赖以生存的基础，在矿产资源开发过程中，矿区的生态环境会受到一定影响，因而矿区居民应享受资源开发的红利，得到相应的经济补偿，其也是矿产资源开发利益分配的相关者。

Chang等［3］指出生态补偿机制是遏制环境破坏的重要经济手段。《中华人民共和国企业所得税法》是目前我国政府与企业在矿产资源开发中进行利益分配的主要依据，然而对矿区居民的利益分配仍缺乏相应的法律规范，主要是以各种补偿的方式进行。Tisdell和Harrison［4］认为社会最优补偿政策的制定是复杂的，补偿结果的不确定性可能会对新的投资造成不利影响。目前我国主要是针对矿山土地复垦问题对矿区居民进行土地占用补偿，相关补偿以《土地复垦条例》为准，其中涉及因矿产资源开发对居民进行损失补偿的相关内容，但是对于如何补偿、补偿的标准是什么缺乏明确规定①《土地复垦条例》第十九条规定：土地复垦义务人对在生产建设活动中损毁的由其他单位或者个人使用的国有土地或者农民集体所有的土地，除负责复垦外，还应当向遭受损失的单位或者个人支付损失补偿费。损失补偿费由土地复垦义务人与遭受损失的单位或者个人按照造成的实际损失协商确定；协商不成的，可以向土地所在地人民政府国土资源主管部门申请调解或者依法向人民法院提起民事诉讼。。刘春学［5］、杨从明［6］等人采用博弈分析方法进行研究，发现因资源稀缺导致多方利益主体利益分配不均现象在矿产资源开发中尤为严重，民生问题亟待解决。现实中矿区居民承受着因矿产资源开发破坏生态环境而带来的生活质量下降问题，同时又无法得到与之相匹配的补偿份额，这就不可避免地造成矿山企业在矿产资源开发过程中与矿区居民之间的利益分配矛盾。乌兰［7］、达林太［8］、王承武［9］等人认为，有效开发矿产资源、推动矿区所在地经济发展、改善矿区生态环境的核心问题是矿产资源开发的利益分配问题。朱晓［10］、魏帅［11］等人提出了政府有偿出让矿产资源、矿山企业主体经营开发、矿区居民直接有效参与开发的模式，由三方共同参与矿产资源开发的利益分配。

综上所述，既有研究大多集中于单方面的理论研究，在博弈研究方面视角比较单一，缺乏对利益相关者博弈的系统性分析。现实情况是，矿山企业和矿区居民在矿产资源开发利益分配的博弈中，双方所获取的信息严重不对等，矿区居民很难掌握矿山企业真实的经营状况（盈利或亏损），只能根据矿山企业提供的利益分配方案进行判断，以此决定是否接受矿山企业给予的补偿；同时在博弈过程中，是按照矿山企业先实施策略、矿区居民后实施策略的顺序进行的，所以该博弈属于典型的不完全信息动态博弈。随着双方博弈的不断深入，地方政府作为利益相关者参与进来［12］，其存在两种策略选择：其一，设法满足矿区居民的基本利益诉求，地方政府选择“协助”居民维权；其二，为了提升地方政绩（经济发展、官员升迁等），地方政府选择“漠视”矿区开采利益的不合理分配问题。针对以上问题，本文通过建立博弈模型，研究矿山企业、矿区居民、地方政府之间的博弈关系，试图找出矿产资源开发过程中利益分配的主要矛盾并提出对策建议。

二、矿山企业与矿区居民的不完全信息动态博弈

（一）博弈模型的变量设定和基本假设

矿山企业对矿区居民进行经济利益分配的实施过程往往分为两个阶段。第一阶段为矿山企业与矿区居民进行周旋，商议分配方案、确定分配金额，倘若此时矿区居民对矿山企业给出的分配方案不满意，矿山企业会根据企业的盈利状况以及分配金额的多少，选择追加补偿或者拒绝追加补偿；若矿区居民接受矿山企业的追加补偿方案，则博弈结束；若矿区居民仍然无法接受矿山企业的追加补偿方案，此时博弈便会进入第二阶段。第二阶段中，矿区居民向当地政府寻求帮助，地方政府依据自身利益的考量，选择“协助”或“漠视”矿区居民的诉求，因其中可能存在矿山企业与地方政府官员之间的寻租问题，因而博弈由第一阶段的两方博弈进化为第二阶段的三方博弈。

第一阶段的博弈主体是矿山企业与矿区居民，可在二者利益分配的基础上建立矿山企业与矿区居民的不完全信息动态博弈模型，主要变量说明如表1所示。本文对博弈模型作出如下假设：

表1 主要变量说明

第一，矿山企业与矿区居民作为博弈双方均为完全理性的决策人，双方在进行决策时会遵循自身利益最大化原则，采取对自己有利的措施。

第二，矿区居民会根据矿山企业的经营规模和性质判断企业是否盈利，矿山企业会在考量自身盈利水平并预估矿区居民对企业的判断后提出补偿金额。在实际中，经营规模大的国有企业未必盈利水平很高，经营规模小的民营企业也未必盈利水平有限。矿山企业清楚了解自身的盈利状况，但是矿区居民受限于匮乏的信息往往只能依据矿山企业的经营规模来判断其盈利状况，判断其为盈利企业（P类）的概率为p1，为亏损企业（L类）的概率为p2。

第三，P类和L类矿山企业的总收益分别为μ1和μ2，矿山企业无论是P类或L类都有｛b1，b2｝即｛合理分配，不合理分配｝两种分配方案可供选择。选择b1策略的矿山企业，社会责任意识较强，根据自己的真实盈利水平，将利润的k1部分让渡给矿区居民，矿区居民分得比例为k1；反之，选择b2策略的矿山企业，社会责任意识薄弱，选择瞒报实际利润而不进行合理分配，只愿意将利润的k2部分让渡给矿区居民，矿区居民分得比例为k2，0＜k2＜k1＜1。

第四，将P类矿山企业与L类矿山企业合理分配后企业留存的收益分别设为v1和v2，将P类矿山企业与L类矿山企业合理分配后矿区居民分得的收益设为u1和u2，将P类矿山企业不合理分配比合理分配的收益多出的部分设为w1=(k1-k2)μ1，则P类矿山企业不合理分配后企业留存的收益为v1+w1，P类矿山企业不合理分配后矿区居民获得的收益为u1-w1。同理，将L类矿山企业不合理分配比合理分配的收益多出的部分设为w2=(k1-k2)μ2，则L类矿山企业不合理分配后企业留存的收益为v2+w2，L类矿山企业不合理分配后矿区居民获得的收益为u2-w2。

第五，矿山企业向矿区居民公示补偿金额，此时矿区居民无法判断矿山企业采取的是何种分配方案，其会根据概率p1、p2，同时结合矿山企业给出的补偿金额以及对矿山企业盈利状况的判断，采取{A,D}策略，即同意或者不同意矿山企业公示的补偿金额，A表示同意，D表示不同意，采取D策略的矿区居民会通过各种渠道和方式要求矿山企业追加补偿金额。

第六，矿山企业根据矿区居民所采取的策略，进行下一步决策。若矿区居民采取A策略，则双方博弈结束；若矿区居民采取D策略，则矿山企业会根据自己真实的盈利状况与矿区居民采取的追加补偿方式（如向地方政府投诉维权或是在采矿区静坐示威等）来选择是否追加对矿区居民的补偿金额。若矿山企业采取C策略，表示其为了避免产生冲突矛盾，选择对矿区居民追加补偿金额，λ1μ1和λ2μ2分别为P类、L类矿山企业采取C策略时对矿区居民的追加补偿金额（0＜λ1＜k1，0＜λ2＜k2）。此时，矿山企业追加补偿的金额已经是其愿意让渡的最大数额，即除非强制性征收，再无追加的可能。若矿区居民接受追加金额，则双方博弈结束；若矿区居民可接受的最低利益诉求未得到满足，则矿区居民选择继续采取S策略，即双方协调不成功，冲突激化，从而使双方产生冲突成本，如矿区居民到矿山企业示威、破坏矿山企业的基础设施等；并且此时矿山企业宁愿与矿区居民发生冲突，也会拒绝再次追加补偿金额。此时，矿区居民的冲突成本为s′，矿山企业的冲突成本为s*。

（二）矿山企业与矿区居民利益分配的博弈分析

矿区居民在接受矿山企业的补偿金额时存在{合理分配，不合理分配}两种情况，而矿区居民面对矿山企业公布的补偿金额所采取的行动策略存在{A,D}和{C,S}两种情况。因此，基于矿山企业是否合理分配可分解为：当矿山企业选择“合理分配”时，其会依照实际盈利状况，合理让渡部分收益给矿区居民；当矿山企业选择“不合理分配”时，其为了减少补偿而隐瞒部分收入，不分配给矿区居民。矿区居民在矿山企业第一次公示补偿金额时如选择A策略，表示矿区居民接受了矿山企业的补偿金额，双方博弈结束；反之如选择D策略，则表示矿区居民不接受第一次公示的补偿金额。此时，矿山企业会选择与矿区居民协商，并在新的分配方案中增加λαμβ的赔偿金额，其中α，β＝（1，2），以满足矿区居民的最低利益诉求；若矿区居民选择C策略，表示矿区居民接受了追加补偿的金额，双方博弈结束；若矿区居民选择S策略，表示矿区居民不满于矿山企业给出的追加补偿金额，并且会与矿山企业产生冲突，矿区居民还需承担一部分冲突成本。

若矿山企业为盈利企业（P类），其经营状况较好，可能会获得合理利润甚至是超额利润，则P类矿山企业与矿区居民利益分配的博弈支付矩阵见表2。通过对矩阵的分析可以得出P类矿山企业和矿区居民在博弈中有以下几种选择：当矿山企业选择“合理分配”时，矿区居民选择第一次不接受，经和解后选择接受；当矿山企业选择“不合理分配”时，矿区居民依旧选择第一次不接受，经和解后选择接受；当矿区居民第一次就接受矿山企业的分配方案时，矿山企业选择“不合理分配”；当矿区居民选择第一次不接受，经和解后选择接受时，矿山企业的选择仍为“不合理分配”；当矿区居民两次谈判都不接受，最后发生冲突时，矿山企业依旧选择“不合理分配”。因此，无论矿区居民作出何种选择，P类矿山企业在保证其利益最大化的原则上，都会选择b2，即“不合理分配”是P类矿山企业的严格占优策略。

表2 P类矿山企业与矿区居民利益分配的博弈支付矩阵

若矿山企业为亏损企业（L类），其经营状况不好，可能会获得低利润甚至是负利润，则L类矿山企业与矿区居民利益分配的博弈支付矩阵见表3。通过对矩阵的分析可以得出L类矿山企业和矿区居民在博弈中有以下几种选择：当矿山企业选择“合理分配”时，矿区居民选择第一次不接受，经和解后选择接受；当矿山企业选择“不合理分配”时，矿区居民依旧选择第一次不接受，经和解后选择接受；当矿区居民第一次就接受矿山企业的分配方案时，矿山企业选择“不合理分配”；当矿区居民选择第一次不接受，经和解后选择接受时，矿山企业的选择仍为“不合理分配”；当矿区居民两次谈判都不接受，最后发生冲突时，矿山企业依旧选择“不合理分配”。因此，无论矿区居民作出何种选择，L类矿山企业在保证其利益最大化的原则下都会选择b2，即“不合理分配”是L类矿山企业的严格占优策略。

表3 L类矿山企业与矿区居民利益分配的博弈支付矩阵

（三）博弈的海萨尼转换

根据上述分析可知，“不合理分配”是矿山企业的严格占优策略，虽然矿区居民不能准确判断矿山企业的分配方案是否合理，但矿区居民知道无论矿山企业是盈利还是亏损，矿山企业都会偏好选择b2策略。因此，在无论哪种类型的矿山企业都会优先选择b2策略的背景下，本文引入虚拟自然人进行海萨尼转换，可以得到矿山企业与矿区居民利益分配的不完全信息动态博弈模型，如图1所示。

图1 矿山企业与矿区居民利益分配的不完全信息动态博弈模型

（四）博弈模型求解

由于λαμβ和s*的大小关系未定，因而对矿山企业来说，矿区居民采取D策略后的最优策略是与矿山企业达成和解，接受追加的补偿金额，此时矿山企业是在完全信息下的动态博弈，可以通过逆向归纳法得到矿山企业应对矿区居民D策略的最优策略。

信号博弈的精炼贝叶斯均衡是策略组合（B*Pi，a*B）和p（pi|B）的组合，根据信号博弈求解要求满足如下条件：

第一，设矿区居民对矿山企业的信号bt(t=2)=B，在矿区居民对P类、L类矿山企业可能发送信号B的信念为p（pi|B）的条件下，矿区居民会选择策略a*(b2)，并使自身效用最大化，即a*(b2)满足下式：

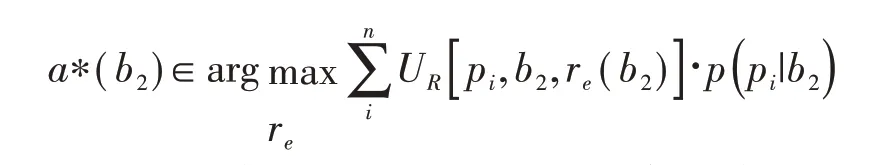
第二，矿山企业无论是P类还是L类，都会选择策略b2*(pi)，使自身效用最大化，即b2*(pi)满足：

第三，对于矿山企业采取的所有策略，矿区居民对应于bt(t=2)=B的信息集所持有的信念必须取决于贝叶斯法则和企业策略，即应满足：

第四，根据前文分析，矿山企业与矿区居民之间可得到如下精炼贝叶斯纳什均衡：

（1）当λ1μ1＜s*时，由λ2μ2＜λ1μ1，可知λ2μ2＜s*。矿山企业最优策略组合为（b2，b2），矿区居民的信念p=0.72①2019年《中国统计年鉴》显示，我国从事石油和天然气开采业的企业单位数为115个，其中亏损企业单位数41个；从事煤矿开采业企业单位数为4239个，其中亏损企业单位数1160个。以上两类企业中亏损企业数量合计1201个，占总数的27.58%，从而可以得出矿山企业为P类的概率p1=0.72，为L类的概率p2=0.28。因矿区居民无法判断矿山企业采取的是何种分配方案，其会根据概率p1=0.72、p2=0.28对是否接受矿山企业的分配方案作出判断，所以有矿区居民的信念p=0.72。。此时无论P类还是L类矿山企业，为实现利益最大化，都会在矿区居民拒绝第一次分配方案时，选择与矿区居民协商，而不是与矿区居民发生冲突。同时，无论矿区居民认为矿山企业是P类还是L类，当其在不接受第一次分配方案时，都会选择接受第二次分配方案，而不是选择冲突，这样才能够使自身效用最大化。因此，此时矿山企业与矿区居民的博弈均衡解为{（b2，b2）,（D，D）}。

由上述分析可知，对于矿山企业来说，其存在严格占优策略即“不合理分配”，矿区居民选择“接受”或“不接受”取决于对矿山企业的先验判断。若先验判断矿山企业为P类的概率大，则矿区居民会选择先不接受第一次分配方案，然后在协商时接受第二次方案；若先验判断矿山企业为L类的概率大，则矿区居民会选择在矿山企业给出第一次分配方案时就接受。

（2）当λ2μ2＜s*＜λ1μ1时，矿山企业的最优策略组合为{b2，b2}，矿区居民的信念p=0.72。此时P类矿山企业为实现利益最大化，会在矿区居民拒绝第一次分配方案时，不再与矿区居民协商，而是选择冲突；而L类矿山企业会在矿区居民拒绝第一次分配方案时，选择与矿区居民进行协商。对于矿山企业来说，其存在严格占优策略“不合理分配”，矿区居民选择“第一次就接受”还是“第一次不接受”取决于对矿山企业的先验判断。若先验判断矿山企业为P类的概率大，则矿区居民会选择“第一次就接受”；反之，若先验判断矿山企业为P类的概率小，则矿区居民会选择先不接受第一次分配方案，然后在协商时接受第二次分配方案。因此，在矿区居民认为矿山企业是P类时面临两种选择，即“第一次就接受”和“第一次不接受”，此时矿山企业不会再与矿区居民进行第二次协商，而是选择与矿区居民发生冲突；在矿区居民认为矿山企业是L类时也面临两种选择，即“第一次就接受”和“第一次不接受而第二次接受”。矿区居民接受与否的期望收益函数分别为：

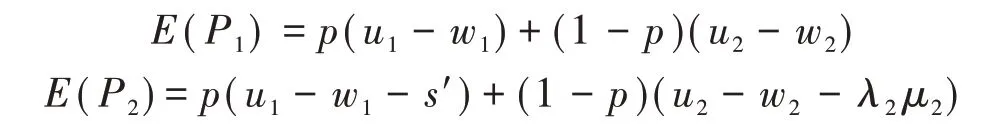
假设矿区居民无论是否接受其预期损失相同，即E(P1)=E(P2)，可得矿区居民接受与否的最优概率为：p*=λ2μ2∕(λ2μ2+s′)。

当p=0.72＞p*时，矿区居民先验判断矿山企业为P类的概率大，选择“第一次就接受”的期望收益大于“第一次不接受”；矿区居民先验判断矿山企业为P类的概率小，选择“第一次就接受”的期望收益小于“第一次不接受”。因此，此时矿山企业与矿区居民的博弈均衡解为{（b2，b2）,（A，D）}。

（3）当λ2μ2＞s*时，由λ2μ2＜λ1μ1，可知λ1μ1＞s*。矿山企业的最优策略组合为（b2，b2），矿区居民的信念p∈［0，1］。此时无论是P类矿山企业还是L类矿山企业，为实现利益最大化都会在矿区居民拒绝第一次分配方案时，不再与矿区居民协商，而是选择冲突。因此，无论矿区居民认为矿山企业是P类还是L类，其要么接受第一次分配方案，要么与矿山企业发生冲突。矿区居民接受与否的期望收益函数分别为：

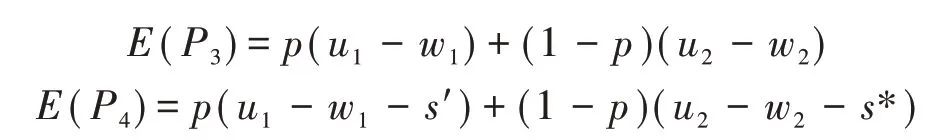
假设矿区居民无论是否接受其预期损失相同，即E(P3)=E(P4)，此时矿区居民接受与否的最优概率不存在。这意味着，当λ2μ2＞s*时，矿区居民要想达成效益最大化的目的，只有选择在第一次就接受矿山企业的分配方案。

由上述分析可知，在设定了一定假设条件下的矿山企业与矿区居民利益分配的不完全信息动态博弈中，矿区居民会依据其所获得的信息理性地预期矿山企业对其让渡的补偿金额，而矿山企业也会根据矿区居民的行为来确定进一步采取的策略，从而达到一种混同均衡的状态。该状态传递的信息为：无论盈利或亏损，矿山企业在最初确定对矿区居民的补偿金额时都会采取“不合理分配”策略。

三、矿山企业、矿区居民、地方政府的三方博弈

由于矿区居民在第一阶段的博弈中掌握的信息是不完全的，在第一阶段采取S策略的矿区居民会选择上访以维护自身权益，进而使博弈进入第二阶段。此时博弈主体为矿山企业、矿区居民、地方政府，其中地方政府为协助矿区居民方，矿区居民为投诉检举方，矿山企业为被投诉方，该博弈是对第一阶段博弈的补充。

当矿区居民与矿山企业之间的矛盾冲突难以化解时，矿区居民选择向地方政府寻求帮助，由地方政府介入与矿山企业协商化解冲突。作为矿区居民，其有“维权”和“不维权”两种策略选择，只有矿区居民主动向地方政府提出维权诉求，地方政府才会有“处理”和“不处理”两种对策。通常情况下，矿山企业出于利益考虑，不会主动支付后续的补偿金额，因此只有地方政府选择帮助矿区居民维权，矿区居民才有可能获得令他们满意的补偿金额。

因此，假设第一阶段的博弈以矿区居民与矿山企业发生冲突而告终，此时对于矿区居民而言，有{维权，不维权}两种策略选择，只有矿区居民主动向地方政府提出维权诉求，地方政府才会有相应的对策。矿山企业出于自身利益最大化的考虑，一旦与矿区居民发生冲突，不会再选择补齐后续的补偿金额。地方政府有两种策略选择：一是为了维护当地社会稳定，选择协助矿区居民维权，为其争取最低利益诉求，如果证实矿山企业没有遵守相关政策对矿区居民进行补偿，则对矿山企业进行一定的处罚（此种情形以下简称为“协助”）；二是地方政府为保证当地的经济发展，私下对矿山企业作出偏袒企业的承诺，选择漠视矿区居民诉求，对其上访维权的诉求采取不作为的态度（此种情形以下简称为“漠视”）。

在矿区居民与P类矿山企业发生冲突的情况下，P类矿山企业已经获得的利益W1=v1+w1-s*，矿区居民已经获得的补偿金额U1=u1-w1-s′。矿区居民为使自己的最低利益诉求V1=u1-w1+λ1μ1得到满足，会选择上访维权，向地方政府寻求帮助，诉求其余下的利益v3=λ1μ1+s′。同理，在矿区居民与L类矿山企业发生冲突的情况下，L类矿山企业已经获得的利益W2=v2+w2-s*，矿区居民已经获得的补偿金额U2=u2-w2-s′。矿区居民为使自己的最低利益诉求V2=u2-w2+λ2μ2得到满足，也只有选择向地方政府上访维权以寻求帮助，诉求其余下的利益v4=λ2μ2+s′。

假设矿区居民向地方政府申请维权的成本为C1；地方政府帮助矿区居民维权时，需要对矿区居民所举报的矿山企业进行调查采证，耗费成本为C2；发现矿山企业确实存在侵害矿区居民合法权益的行为时需对其进行处罚，所获罚款收益为F1；勒令矿山企业补齐对矿区居民的赔偿款，此时地方政府获得的政绩和荣誉收益为T。若地方政府未对矿区居民提出的维权诉求进行处理，则矿区居民与矿山企业的冲突进一步恶化，由此而引发矿区居民继续上访等给地方政府带来的负面形象损失以及上级政府处罚损失为F2。假设只有矿区居民和地方政府共同努力才能使矿区居民获得剩余补偿，由此可构建矿山企业、矿区居民、地方政府的博弈支付矩阵，详见表4。

表4 地方政府、矿山企业、矿区居民的博弈支付矩阵

由表4可知，当λ1μ1≥C1-s′或λ2μ2≥C1-s′时，如果地方政府将矿区居民的利益放在首位，则矿区居民的最优策略是“维权”；对地方政府来说，如果矿区居民向地方政府寻求帮助，其最优策略是“协助维权”。但是，无论双方的策略选择如何，矿区居民都将成为矿区生态破坏的最大受害者。此时的纳什均衡为{维权，协助维权}，该均衡为好的纳什均衡。只有提高对服务型政府的嘉奖，降低矿区居民维权成本C1，才能在这一策略上达到均衡状态。若矿区居民对矿山企业给出的补偿金额不满，出于自身利益考虑一定会采取维权措施，向政府部门举报并提出利益诉求，此时地方政府应从全局出发，充分发挥其协调管理职能，努力化解矿山企业与矿区居民的矛盾冲突，保障矿区居民的合法权益。

四、结论与建议

（一）结论

本文通过构建矿山企业与矿区居民利益分配的不完全信息动态博弈模型以及加入地方政府的第二阶段事后博弈模型发现，矿山企业以何种分配比例对矿区居民进行利益分配对于矿区居民是否接受分配方案具有重要影响，而矿区居民本身是否接受矿山企业公示的补偿金额在很大程度上决定了地方政府是否介入矿山企业的利益分配。

矿山企业作为完全理性的决策人，势必会选择有利于自己的分配方案，“不合理分配”是矿山企业的严格占优策略，而矿区居民的维权成本越低，越倾向于向地方政府寻求帮助。此时地方政府应帮助矿区居民获得其应得的补偿金，一旦地方政府介入就意味着矿山企业必须进行合理的利益分配，因此矿山企业会尽可能避免冲突而选择向矿区居民让渡一部分利润作为补偿。然而在实际中，矿山企业往往难以量化合理的利益分配比例，一旦地方政府放松监管，或是矿区居民的维权成本高，矿山企业就很有可能消极应对，侵犯矿区居民的合法利益，以实现自身利润最大化。

（二）建议

1.设立矿区纠纷处理机构，降低矿区居民维权成本。目前矿区居民因争取更合理的经济补偿而与矿山企业发生冲突的现象时有发生，这与矿区居民的维权意识及维权渠道有关。当矿区居民认为矿山企业侵犯其利益时，在维权意识淡薄的情况下，其更易与矿山企业发生直接冲突，而不是采取其他途径进行维权。因此，要保障矿区居民的基本权益，首先应引导矿区居民采取正确的维权行为，避免矿区居民与矿山企业发生冲突；其次应降低矿区居民的维权成本，地方政府应设立专门的矿区纠纷处理机构，由专人专线高效解决问题，杜绝各部门之间的“踢皮球”行为，同时开通维权热线，积极处理居民投诉。需要注意的是，只有矿区居民正确维权，才有可能增加地方政府的政绩和荣誉收益。

2.地方政府按矿山企业实际情况确定分配比例，积极督促矿山企业进行合理补偿。目前我国矿山企业补偿矿区居民的标准还不清晰，而只有矿区居民主动向地方政府提出维权诉求，地方政府才会有“处理”和“不处理”两种对策，即地方政府的行动完全是在矿区居民与矿山企业博弈后进行的。为维护矿区居民的合法利益，地方政府应积极转变角色，针对辖区内不同的矿山企业，可通过实地调研和财务分析等途径，对其营收状况及生产经营活动对矿区居民生活造成的影响等进行综合考量，通过加权等科学方法计算出适用于不同企业的分配比例，并向社会公示。矿山企业应按照此比例进行利益分配，增强是否按比例进行分配的信息披露透明度，接受当地政府和矿区居民的监督，从根本上化解与矿区居民之间的矛盾，促进矿区的持续和谐发展。