不等式在中考中的考点

文／吴 凡

不等式是历年中考题目中的常考题型，主要考查：解不等式或解不等式组、函数与不等式的综合应用，现就这两种题型加以解析、总结。

常见考点1 解不等式或不等式组

此类题型大多是运用解不等式组的方法，求解该不等式组的解集，并在数轴上表示出解集或判断其整数解等。

例1（2021·江苏淮安）解不等式组：

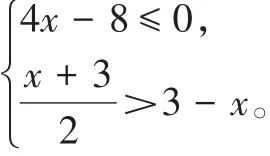
【分析】分别求出每一个不等式的解集，再借助于数轴确定不等式组的解集。

解：解不等式4x-8≤0，得x≤2，

所以，不等式组的解集为1＜x≤2。

【点睛】本题考查的是解一元一次不等式组，正确求每一个不等式解集是基础，熟知“同大取大，同小取小，大小小大中间找，大大小小找不到”是解答此题的关键。

例2（2017·江苏南京）解不等式组请结合题意，完成本题的解答。

（1）解不等式①，得____。

依据是：____。

（2）解不等式③，得____。

（3）把不等式①、②和③的解集在数轴上表示出来。

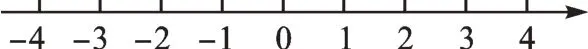
（4）从图中可以找出三个不等式解集的公共部分，得不等式组的解集为____。

【分析】本题主要考查不等式组的解法，同时理解每个不等式的求解依据，会在数轴上表示其解集，最终确定该不等式组的解集。

解：（1）x≥-3。

不等式两边乘（或除以）同一个负数，不等号的方向改变。

（2）x＜2。

（3）

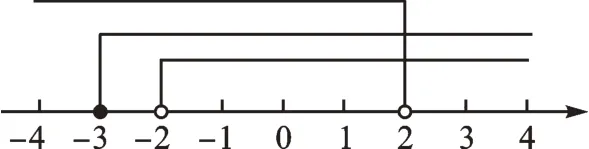
（4）-2＜x＜2。

【总结】此类型题重点考查不等式组的解法：先分别求出每个不等式的解集，再在数轴上表示各不等式的解集，并会结合数轴来确定解集，或者根据口诀“同大取大，同小取小，大小小大中间找，大大小小找不到”确定该不等式组的解集。

常见考点2 函数与不等式的综合应用

例3（2020·江苏南京）已知反比例函数的图像经过点（-2，-1）。

（1）求k的值。

（2）完成下面的解答。

解：解不等式①，得 。

把不等式①和②的解集在数轴上表示出来。

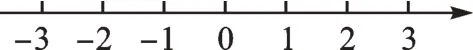
从图中可以找出两个不等式解集的公共部分，得不等式组的解集为____。

【分析】第（1）问利用待定系数法求解即可；第（2）问按照步骤移项、合并同类项、系数化为1求出不等式①的解集，根据反比例函数的图像求出不等式②的解集，进而求出公共部分即可。

解：（1）因为点（-2，-1）在反比例函数y=的图像上，所以点（-2，-1）的坐标满足y=

（2）解不等式①，得x＜1。

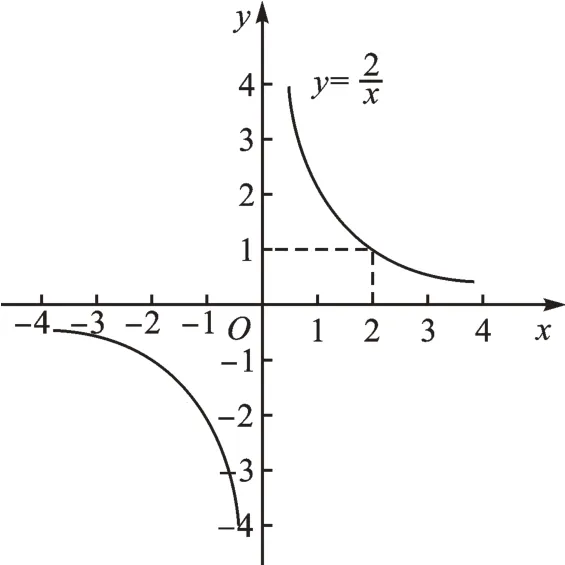
∵当y=1时，x=2，

∴根据函数的图像（如图1），得不等式②的解集为0＜x＜2。

把不等式①和②的解集在数轴上表示出来：

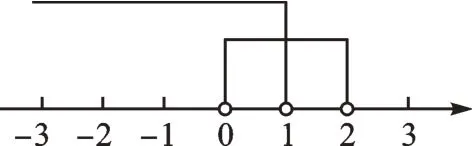
从中可以找出两个不等式解集的公共部分，得不等式组的解集为0＜x＜1。

【总结】本题考查了用待定系数法求反比例函数表达式，利用反比例函数图像解不等式，以及不等式组的解法。对于函数与不等式的综合题型的考查，同学们可以根据题意进行分析判断，并合理借助不等式的思想控制单一变量，从而求得某些未知数的取值范围，同时也可借助数形结合，列出相应的不等式或不等式组，解出该不等式或不等式组即可解决问题。