注重典型 掌握本质

文／何君青

在近些年的中考中，各地普遍从不同侧面、不同角度对方程与不等式知识进行比较全面、系统的考查。大部分试题通过直接考查方程与不等式的意义与解法，突出对基础知识与基本技能的考查；通过设置现实问题情境，考查同学们列方程与不等式解决实际问题的能力，突出对数学建模和数学应用的考查；通过设置综合性问题，考查同学们对方程与不等式的灵活运用，突出对方程思想的考查。本文就以一些典型的考题为例进行剖析，以期对同学们的学习有所帮助。

一、方程与不等式解法的考查

方程与不等式的解法是初中数学的主要工具之一，是数学的基础知识和基本技能，各地大部分采用直接考查的方式对其进行考查。考题主要涉及一元一次方程、二元一次方程（组）、分式方程、一元二次方程、一元一次不等式（组）等五种类型。

例1解方程：

解：方程两边同时乘12，

得4（2x+1）-3（x-2）=12。

去括号，得8x+4-3x+6=12。

合并同类项，得5x=2。

【点评】本题是对一元一次方程的解法进行考查。一般情况下，解一元一次方程的五个步骤是：去分母、去括号、移项、合并同类项、系数化为1。要注意的是：在“去分母”环节，不要漏乘；在“移项”环节，要变号。

例2

解法1：由①，得x=-3y-1。③

将③代入②，得3（-3y-1）-2y=8。

解这个方程，得y=-1。

将y=-1代入③，得x=2。所以，原方程组的解是

解法2：①×3，得3x+9y=-3。③③-②，得11y=-11。

解这个方程，得y=-1。

将y=-1代入①，得x=2。

【点评】本题是对二元一次方程组的解法进行考查。“消元”是解多元方程组的思想，一般情况下，解二元一次方程组有两种常用的方法：代入消元法、加减消元法。

例3解方程

解：方程两边乘（x-1）（x+1），

得x（x+1）-（x-1）（x+1）=3。

解得x=2。

检验：当x=2时，（x-1）（x+1）≠0。

所以，原分式方程的解为x=2。

【点评】本题是对分式方程的解法进行考查。一般情况下，解分式方程的步骤是：换（将分式方程转换成整式方程）、解（解整式方程）、验（检验得到的解是否为增根）。要注意的是：分式方程转换成整式方程的过程不一定是等价变形，故而最后一定要验根。

例4解方程：x2-2x-3=0。

解法1：移项，得x2-2x=3。

配方，得x2-2x+12=3+12，（x-1）2=4。

由此可得x-1=±2，

x1=3，x2=-1。

解法2：将x2-2x-3因式分解为（x-3）（x+1），得（x-3）（x+1）=0。

由此可得，x1=3，x2=-1。

【点评】本题是对一元二次方程的解法进行考查。“降次”是解高次方程的思想，一般情况下，解一元二次方程有这些常用方法：直接开平方法、配方法、公式法、因式分解法。

例5解不等式组

解：解不等式①，得x≤1。

解不等式②，得x＞-2。

所以，不等式组的解集是-2＜x≤1。

该不等式组的整数解是-1，0，1。

【点评】本题是对一元一次不等式组的解法进行考查。不等式组中每一个不等式解集的公共部分即为该不等式组的解集，故而在解不等式组时，先要求出每一个不等式的解集。

二、方程与不等式应用的考查

各地普遍创设情境，以实际应用的方式，考查列方程或不等式解决实际问题的能力。我们要特别关注的是，部分试题会要求利用方程或不等式的结果，对实际问题作出判断与预测，或对实际问题设计解决方案。

例6彭老师到超市购买大米。第一次按原价购买，用了105元。几天后，遇上这种大米8折出售，他用140元又买了一些，两次一共购买了40kg。这种大米的原价是多少？

解：设这种大米的原价为每千克x元。

解这个方程，得x=7。

经检验，x=7是所列方程的解。

答：这种大米的原价为每千克7元。

【点评】本题从生活中“购买大米”的实际问题出发，贴近生活，考查列分式方程解决问题的能力，具有较好的推广性。同学们要注意的是：用分式方程解决实际问题，最后依然需要检验。

例7用一条长20cm的绳子能否围成一个面积为30cm2的矩形？如果能，说明围法；如果不能，说明理由。

解：设矩形的长为xcm，则宽为（10-x）cm。

根据题意，得x（10-x）=30，

即x2-10x+30=0。

因为Δ=b2-4ac=102-4×30=-20＜0，

所以此一元二次方程无实数根。

答：用一条长20cm的绳子不能围成一个面积为30cm2的矩形。

【点评】题目在考查列一元二次方程的同时，更关注对实际问题的理解能力的考查。同学们需注意的是：在判断“几何图形是否能够构成”时，若能构成，则能算出具体的值；若不能构成，则不能找到一个符合条件的值，或是无实数根，或是算出的根不在题目的实际范围内。

例8某地计划对矩形广场进行扩建改造。如图1，原广场长50m，宽40m，要求扩充后的矩形广场长与宽的比为3∶2。扩充区域的扩建费用为每平方米30元，扩建后在原广场和扩充区域都铺设地砖，铺设地砖费用为每平方米100元。如果计划总费用为642000元，扩充后广场的长和宽应分别是多少米？

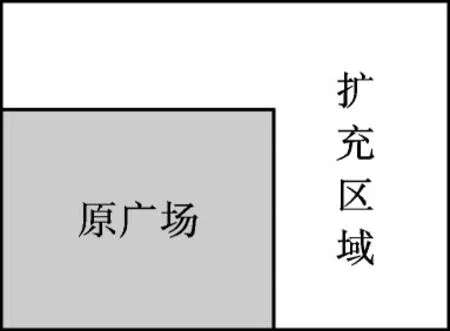
图1

解：设扩充后广场的长为3xm，宽为2xm。

根 据 题 意，得3x·2x·100+30（3x·2x-50×40）=642000。

解得x1=30，x2=-30（不合题意，舍去）。

所以3x=90，2x=60。

答：扩充后广场的长和宽应分别为90m和60m。

【点评】本题以“广场改造”为背景，考查列一元二次方程解决实际问题的能力。同学们首先应根据题意表示出铺设地砖区域和改造广场的费用，再根据题目中存在的等量关系，列出方程，算出相应的结果。同学们在遇到此类问题时需特别注意，应检查算出的结果是否符合实际情况，若不符合，需要舍去。