一种精妙的数据重建方法:网函数插值法
陈启宏, 张兆田, 邱 钧
(1.上海财经大学, 上海 200433; 2.国家自然科学基金委员会, 北京 100085; 3.北京信息科技大学, 北京 100101)
0 引言
数据重建通常是由函数在子流形的相关信息,重建其在高维流形的函数值。CT(Computed Tomography)就是由函数在系列直线上的积分构成的低维投影数据集,重建高维函数。网函数插值是由函数在高维流形边界上的探测数据,重建高维流形上的函数(近似)值。
网函数插值问题是由勘查重力场数据寻找矿藏实际需求驱动的。重力场通常是由大范围的背景区域重力场和由局部地质体(含矿体)引起的局部异常重力场构成。重力勘查不可缺少的步骤之一就是,依据野外获取的大量网格点上重力探测数据,分离区域重力场,进而获得由局部地质体(含对寻找油气和煤田有重要意义的地质构造和规模巨大的矿体)引起的局部异常重力场分布[1]。
1 网函数插值法
简而言之,网函数插值法是由数学上直纹面构造曲面的一种方法。它由不同的三个直纹面构成,其中两个是作为近似曲面的直纹面,第三个是作为全局调整的直纹面。不失一般性,以二元网函数插值为例,阐述具体构造算法。
1.1 二元网函数插值及其余项
在xOy平面上一闭矩形区域D={(x,y)|x0≤x≤x1,y0≤y≤y1}上,其四条边界曲线记为:
u0={(x0,y),f(x0,y)|y0≤y≤y1}
(1)
u1={(x1,y),f(x1,y)|y0≤y≤y1}
(2)
λ0={(x,y0),f(x,y0)|x0≤x≤x1}
(3)
λ1={(x,y1),f(x,y1)|x0≤x≤x1}
(4)
假设函数f(x,y)在矩形区域D上是连续的。可用如下方法,由函数f(x,y)在矩形区域D边界上的值,计算函数f在D内任一点的近似值。

图1 曲面的四条边界线z=F(x,y):μ0,μ1,λ0,λ1
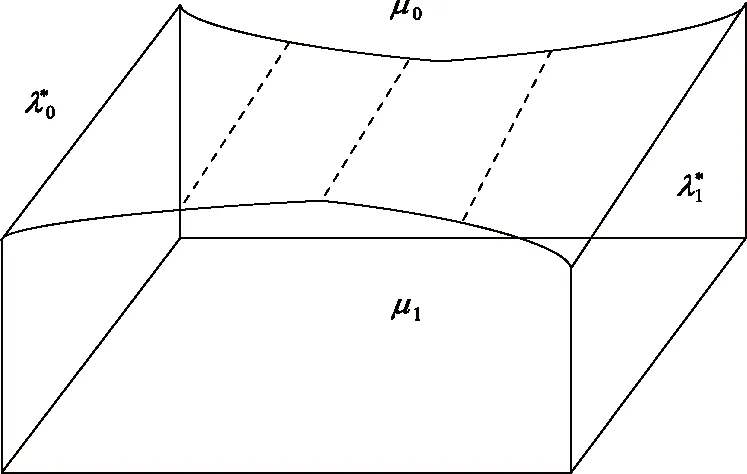
图2 直纹面:z=F1(x,y)
这里从几何角度,通过三张直纹面在矩形区域D上构造一曲面F(x,y),作为函数f(x,y)的近似(以下函数和曲面视为相同含义)。
第一步:设平面y=yq与曲线u0、u1相交于两点,将这两点用直线段联结起来。对于[y0,y1]中任意一数yq,均如上方公式作直线段,这样得到第一张直纹面,记作z=F1(x,y)。
第二步:对于[x0,x1]中任意一点xq,设平面x=xq与曲线λ0、λ1相交于两点,将这两点用直线段联结起来,这样构成第二张直纹面,记作z=F2(x,y)。

图3 直纹面z=F2(x,y)

图4 直纹面z=F3(x,y)
最后,由三张直纹面构造的网函数插值曲面为:z=F(x,y)。其中
F(x,y)=F1(x,y)+F2(x,y)-F3(x,y)
(5)
不难看出,近似曲面F(x,y)在区域D的边界上与f(x,y)取值相等,而直纹面F1(x,y)、F2(x,y)保留了在区域D的边界上与f(x,y)比较接近的部分,用直纹面F3(x,y)在区域D上整体调整F1(x,y)+F2(x,y)与f(x,y)偏差较大的部分。

由此可见,区域D面积A越小,函数f与网函数插值法函数F的逼近程度越高。偏导数最大值M与函数f在区域D上的起伏大小有关。对于在区域D上变化较平缓的函数,网函数插值函数与f的逼近程度也就较高。
1.2 矩形网函数插值的算子表示
上述近似曲面构造过程中,F3由F1和F2计算得来的,进而网插值函数F可用算子简洁表示:
F=F1⊗F2=F1+F2-F1F2
(6)
式中,⊗为布尔和。
1.3 相应的偏微分方程边值问题的解空间
假设F(x,y)在区域D的边界上二次连续可微,则由三张直纹面构造的函数F满足偏微分方程:
(7)
这里函数F的解空间可表示为:
F(x,y)=φ(x)+yφ1(x)+ψ(y)+xψ1(y)
(8)
φ(x)、φ1(x)在区间[x0,x1],ψ(y)、ψ1(y)在区间[y0,y1]上均为二次可微函数[1]。从上式可见,偏微分方程边值问题解F的解空间具有广泛的选择性,可解释为具有良好的函数逼近能力。
若函数f属于网函数插值法所限定的函数类型,则网插值函数F计算的值是精确的。例如,f为三次多项式函数,则F=f。正是由于重力区域异常通常可由不高于三次的二元多项式拟合,符合网函数插值法的应用条件,因而在重力勘查数据处理中取得了理想效果。
1.4 矩形网函数插值的面积加权简洁计算格式
利用上述三张直纹面构造的矩形网函数插值,可得到其与面积有关的简洁计算格式。设D是xOy的平面上的一矩形,D的四个角点记作Pi(i=1,2,3,4)。假设f是定义在D上的连续函数,过Q点作平行于D的四条边的两条平行线,交四条边于四个点记作Qj(j=1,2,3,4)。
过Q的两条平行线将面积为A的矩形分成四块小矩形,小矩形面积记作Ai(i=1,2,3,4),如图5。
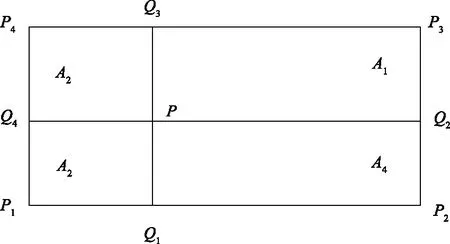
图5 矩形剖分
则上述三张直纹面可分别表示为:
F1(Q)=[(A2+A3)f(Q2)+(A4+A1)f(Q4)]/A
(9)
F2(Q)=[(A1+A2)f(Q1)+(A3+A4)f(Q3)]/A
(10)
F3(Q)=[A1f(P1)+A2f(P2)+A3f(P3)+A4f(P4)]/A
(11)
因此,网函数插值法表示为:
F(Q)=F1(Q)+F2(Q)-F3(Q)
(12)
从计算格式上看出,区域D上任一点Q的计算值,均由在区域边界上的相应8个已知值线性表示。其中,线性系数是相应小矩形面积与大矩形面积的比值,取决于点Q的几何位置,其与坐标系的选择无关[1]。因此,该算法简单,易于计算。
2 网函数插值法应用案例
2.1 网函数插值法在重力勘查中的应用
20世纪 70 年代中期至 80 年代初,针对内蒙古地质局刘士毅先生提及关于勘查重力场数据处理的实际需求,内蒙古大学邱佩璋先生带领团队与内蒙古物探队刘士毅、郭积忠等紧密合作,首先将网函数插值法用于重力勘查区域场校正。当时对鄂尔多斯含油气盆地北部 750 km2的 1∶200 000 重力普查资料,用网函数插值法等作区域校正。与通常采用的圆周法和趋势分析法相比,网函数插值法计算结果表明,共 35 个大小不同的局部异常全都得到了突出,异常特征更清晰、形态更完整。相关理论计算结果后期被实地勘探所证实。网函数插值法的成功创新应用,为重力勘查做出了重要贡献,相关工作被授予地质矿产部科技进步奖。
网函数插值法能够成功地应用于地质勘探领域[2-3],主要得益于两点:其一是该算法结构十分简洁,便于计算机实现;其二是该算法适用于由良好的解空间包含的函数类,适合于分离大小不一、形态各异的局部异常。改进后的方法为分离更高阶次的区域场创造了可能性,便于分离大局部异常中更次级的小局部异常。该方法保证精度的关键是,使四条边界线上待分离局部异常和旁侧局部异常的影响最小。
2.2 网函数插值法在植物群落种群分布格局中的应用
20世纪80年代中期,内蒙古大学数学和生物学研究人员杨在中、郝敦元和杨持等将网函数插值法应用于生态研究中,给出一种研究植物群落种群分布格局的新方法[4]。实践表明,网函数插值法可有效地应用于生物群落种群分布格局的研究[4-5]。新方法避开了英国著名生态学家 Greig-Smith 提出“邻接格子样方法”面临的数据统计量大、难于计算等问题[6],在实践中得到推广应用[3]。
3 相关研究进展
(1)鉴于地貌环境复杂、勘探测线多样性,邱佩璋先生研究团队把矩形网函数插值法扩展到三角网函数插值法,更灵活适应勘查重力场计算[7]。
(2)基于函数类特点和目标函数先验知识,发展了基于数据驱动和模型驱动的网函数插值方法,即改进的网函数插值法[8]。若预先测知函数f的形态,但其数学表达式不符合网函数法所限定的函数类型。如果可通过数学变换T,使得T(f)成为(近似)符合网函数插值法所限定的函数类型,则网函数F计算的值T(f)是(近似)精确的,再对F进一步做数学逆变换T-1就可得到待插函数f。
(3)网函数插值法可推广到n维空间(m)网[9]。例如,一维网函数插值与二点线性插值、三点抛物插值等密切相关。这给出一种构造曲线或曲面的新视角。
(4)利用网函数插值生成 Coons 型分形曲面,曲面形态自然并可保持分形特征[10]。
(5)网函数插值方法可有效地重建探测过程中的不完全数据或在数据传输过程中的局部信息缺损[11-12]。
(6)CT是由系列探测网格点上的探测数据,利用切片定理重建目标图像。如果探测数据不完全,在一定条件下,也可通过网函数插值方法进行数据重建,重构出近似的目标图像。
注:邱佩璋先生1951年毕业于上海交通大学数学系,进入中科院数学所,师从吴新谋先生,研究偏微分方程基本解、Hadamard理论等。1957年响应党和国家号召支援边疆,参与组建内蒙古大学数学系。网函数插值思想萌发在70年代,在发现不完全Huyghens现象,揭示了基本解升维结构,及其展开系数对称性引起的奇特性质,进而形成了结点网产生器的原始思路和方法。当年由重力勘查数据处理的实际探寻矿藏这个重大需求而牵引,邱佩璋先生领导的理论计算团队与刘士毅先生带领的内蒙物探实践团队经过多年的合作研究与迭代演进,网函数插值法在80年代逐步完善,并在区域场校正等等实践中发挥了重要作用。鉴于网函数插值法在重力勘查中的成功运用,1980年,邱佩璋先生等获得了内蒙古自治区的科技进步三等奖,并荣获内蒙古自治区先进科技工作者称号。在邱佩璋先生逝世周年之际,谨以此文缅怀先生教诲。
致谢
感谢中国地质调查局发展研究中心刘士毅研究员在本文撰写过程中的指导、修订和支持,感谢北京信息科技大学刘畅老师等对该文稿的修订整理。

