X射线相位衬度成像的起源、发展和展望
朱佩平, 廖可梁, 何其利, 罗 亮, 葛永帅
(1.中国科学院 高能物理研究所, 北京 100049; 2. 济南汉江 光电科技有限公司, 济南 250024; 3. 清华大学 航天航空学院, 北京 100084; 4. 中国科学院 深圳先进技术研究院, 深圳 518055)
0 引言
在过去100多年里,传统的基于吸收衬度的X射线成像技术不仅在临床医学、安全检查和工业无损检测等领域得到了广泛的应用,而且研发出微米和纳米分辨的X射线显微镜,为科学研究提供了高分辨的研究手段。然而,这种基于吸收机制的X射线成像技术仅适合观察重元素样品,而不适合观察轻元素样品。例如,目前的X射线医学成像对人体骨骼观察得比较清楚,而对人体软组织成像模糊。这其中的原因在于,人体软组织是由轻元素构成的,轻元素对X射线的吸收弱,不同的轻元素之间产生的吸收差异小,犹如观察水中的玻璃碎片,几乎没有可以察觉的痕迹。因而,需要发展一种方法,来清晰分辨正常组织和癌组织,这就好像要想办法看清楚水中的玻璃碎片。因为,轻元素物质引起X射线的相移值是其吸收衰减值的1000多倍[1,2],所以利用相移产生衬度的X射线相位衬度成像特别适合观察轻元素构成物体。例如,对于波长为0.1 nm的X射线而言,需要经过3 mm碳,才能将X射线的光强衰减一半,而只须透过3 μm碳膜就能使X射线产生0.2π的相移。因此,X射线相位衬度成像在轻元素构成样品成像领域具有巨大的发展潜力。
经过二三十年的发展,尽管已经发展出多种X射线相位衬度成像方法,但是X射线相位衬度成像的应用之路遇到了许多难以解决的困难,远不如人们最初期望的那样顺利。例如,泽尼克相位衬度显微镜方法从可见光波段推广到X射线波段已有多年,可是相位定量化一直是悬而未决的难题,阻碍了X射线相位衬度显微镜和纳米CT的结合。再如,人们普遍对X射线相位衬度成像在医学临床的应用前景抱有巨大希望,期望可以研发出辐射剂量低、相位衬度高的医学临床成像设备。可是,截止目前提出的所有方法,包括以临床为目标的研究进展,都难以在样品的辐射剂量上和传统吸收衬度成像一决高低。
本文对X射线相位衬度成像进行一次追根溯源的回顾,目的是从基础理论到成像方法,搞清楚X射线相位衬度成像的来龙去脉,在此基础上梳理已经发展的各种方法和近年来的新进展,分析不同方法之间的比较优势,力图从中洞察出可能的发展潜力,展望X射线相位衬度成像未来的发展前景。本文第1节追溯相位的起源,第2节梳理利用相位进行成像的理论基础,第3节对X射线相位衬度成像的各种方法进行分类,第4节和第5节分别介绍国际和国内X射线相位衬度成像方法研究新进展,第6节介绍两例临床前期研究进展,第7节展望X射线相位衬度成像在纳米分辨成像和医学临床成像的未来前景。
1 相位的起源
相位来源于麦克斯韦方程组推导出来的电磁波动方程。根据麦克斯韦方程组,在线性、各向同性、非磁和忽略极化的介质中,可推导出的单色标量电磁波动方程[1]
(1)

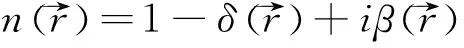
(2)
式中,δ和β分别为相移项和吸收项,并且β≪δ≪1。消除式(1)中随时间简单快速变化的相位振荡因子,可以推导出介质中亥姆霍兹方程[1]
(3)
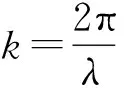
(4)
式中,I为与空间位置有关的光强;Φ为与空间位置有关的相位。利用样品产生光强衰减信号的成像是传统吸收衬度成像,而利用样品产生相位改变信号的成像是相位衬度成像。
历史上,利用相位进行成像有三个里程碑。1935年,荷兰科学家Frits Frederik Zernike发明相位衬度显微镜,1953年荣获诺贝尔物理学奖[2]。1948年,匈牙利科学家Dennis Gabor发明全息成像方法[3],1971年荣获诺贝尔物理学奖。1952—1980年,美国科学家David Sayre经过多年研究提出相干衍射成像原理,该原理在1999年被他的学生缪健伟验证[4]。
2 利用相位进行成像的理论基础
虽然介质中亥姆霍兹方程有精确的解析解,但是其中有代数和的开方,难以进行进一步的解析推导。目前,广泛使用的是两个互相补充的近似解析解,分别对应两个波束传播模型:一个是波幅被不均匀介质调制的傍轴平面波传播模型,另一个是波束传播方向被不均匀介质调制的光流线传播模型。
2.1 傍轴平面波传播模型
成像光学是傍轴光学,光束基本上沿着光轴传播,光束偏离光轴的距离远小于其沿光轴传播的距离。为了在傍轴条件下求解介质中亥姆霍兹方程,提出傍轴平面波传播模型。傍轴平面波传播模型的物理图像参见图1,其数学表达式为

图1 傍轴平面波传播模型的物理图像
(5)
式中,A′为被调制的波幅;eikz为轴向平面波传播因子。把式(5)代入式(3),从A的三维变化中剥离简单快速的轴向变化eikz,留下复杂缓变的三维变化A′,介质中亥姆霍兹方程变形为
(6)

(7)
介质中傍轴波动方程有两个典型应用:一个是薄样品内,另一个是样品外的自由传播。
2.1.1 投影光线近似方程
当样品厚度T满足下列条件[5]
(8)
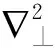
(9)
求解此方程可得出射波幅和入射波幅之间的关系为
(10)

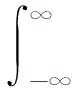
(11)
Φ为样品的相移(即相位改变),其表达式为(参见表1中序号2)

(12)
式(11)和式(12)分别是在薄样品内计算吸收和相移的理论根据。
2.1.2 真空中傍轴波动方程和四个次级结果
(13)
利用二维傅里叶变换,可以证明式(13)的解为[1]
(14)
式中,F和F-1为二维傅里叶变换和逆变换;kx=ksinθx,ky=ksinθy;θx为平面波偏转方向与光轴在x轴方向的夹角;θy为平面波偏转方向与光轴在y轴方向的夹角。把式(14)代入式(5),得
(15)
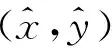
当菲涅耳数足够小时,即
(16)
时,式(15)转化为远场的夫琅禾费衍射
A(x,y,z)
(17)
根据式(11)和式(12),在弱吸收和弱相位条件下,利用菲涅耳衍射,即式(15),可以推导出衬度传递函数[1](contrast transfer function, CTF)
(18)

若在傍轴平面波传播模型式(5)的基础上,进一步把被调制的波幅变形为绝对值和单位复数的乘积,即
(19)
式中,I为可测量的光强;Φ为扣除轴向平面波相位贡献的相位分布,把式(19)代入式(13),则可从真空中傍轴波动方程推导出强度传输方程[1](transport intensity equation, TIE)
(20)
需要指出的是,菲涅耳衍射是透镜成像的理论基础,夫琅禾费衍射是相干衍射成像的理论基础,衬度传递函数和强度传输方程是自由传播成像的理论基础。
2.2 光流线传播模型
当样品不能看为薄样品时,X射线传播方向必然受到样品折射影响,不能再坚持以轴向平面波为核心的数学描述了,于是发展出另一条简化介质中亥姆霍兹方程的思路,把电磁波场看作电磁能量流动场,用光流线来描述光的传播、求解X射线成像问题。光流线传播模型的物理图像参见图2,其数学表达仍然采用式(4),其中I为可测量的光强,Φ为光流线的相位,在傍轴传播条件下,式(4)中相位可表达为

图2 光流线传播模型的物理图像
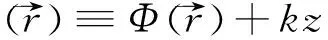
(21)
其中
(22)
在此请注意,式(22)中的相位和式(12)中的相位之间的差别。
把光流线传播模型代入介质中亥姆霍兹方程,即把式(4)代入式(3),可以推导出光线方程[1]
(23)
和光线微分方程[1]
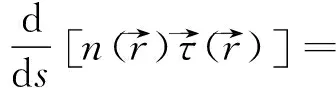
(24)
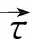

(25)
和光线微分方程

(26)
光流线传播模型为研究厚样品中折射、波面弯曲和散射提供了数学工具,本文在第4.5节将介绍这方面的研究结果。
2.3 单色X射线携带的五种成像信号
比较傍轴平面波传播模型和光流线传播模型,可以发现,前者假设光束不改变传播方向,只能推导出吸收和相移两种信号; 而后者允许光束改变传播方向,不仅能推导出吸收和相移两种信号,而且能推导出相位梯度、相位拉普拉斯和散射角方差三种信号,参见本文4.5节中的说明。表1列出五种信号的数学表达、被积函数和其物理意义。

表1 单色X射线携带的五种成像信号
3 X射线相位衬度成像分类
截止目前,已经发展出干涉法、载波调制法、自由传播法和微束追踪法共四种X射线相位衬度成像方法。下面分别介绍。
3.1 干涉法
利用物光和参考光的干涉,可以把相位变化转换为光强的周期变化,根据光强的周期变化可以提取出样品中的相位信息。已经发展出两种利用干涉的X射线相位衬度成像方法:一个是X射线相位衬度显微镜,另一个是晶体干涉仪成像。
3.1.1 X射线相位衬度显微镜
1935年,为了观察几乎透明的细胞,荷兰科学家Frits Frederik Zernike发明了相位衬度显微镜[2],利用零频光不受样品干扰的性质,把零频光作为参考光,在零频光位置插入相移片,参见图3,改变零频光和物光在成像面上干涉时的相位差,把物光的相位变化转变为光强变化。相位衬度显微镜的原理在20世纪末21世纪初推广到X射线,参见图4。不论是可见光相位衬度显微镜,还是X射线相位衬度显微镜,存在一个长期悬而未决的问题:相移片和相移环侵占了低频空间,引起低频信息失真。80多年了,该问题一直阻碍着相位衬度定量化。

图3 相位衬度显微镜原理示意图

图4 X射线相位衬度显微镜示意图
3.1.2 晶体干涉仪成像
1971年,日本科学家M. Ando等[6]提出,把样品置于晶体干涉仪中的一束光中,参见图5,把样品的透射光束作为物光,把无样品的另一束光作为参考光,利用物光和参考光的干涉,把物光中的相位变化转变光强变化。1995年,日本科学家A. Momose等[7]进一步利用晶体干涉仪,采集相移项δ的投影积分数据,参见表1中序号2,利用逆Radon变换重建了生物样品折射率相移项的三维分布,完成了世界上第一例相位CT实验。

图5 晶体干涉仪成像示意图
3.2 载波调制法
利用样品的折射和散射调制可以测量的光强分布,这个光强分布就是空间载波。根据调制前后的光强分布可以提取样品的折射和散射信息。已经发展出三种利用载波调制的X射线相位衬度成像方法,分别是:衍射增强成像、基于光栅的相位衬度成像和基于散斑的相位衬度成像。
3.2.1 衍射增强成像
1995年,澳大利亚科学家Davis等[8]发表了实验室光源的衍射增强成像的初步结果。1997年,美国科学家D. Chapman等[9]提出定量提取y轴折射角的方法;2003年,美国M. N. Wernick等[10]提出提取y轴散射角方差的方法,参见图6(a)。中国朱佩平等分别在2005年[11]和2015年[12]提出定量提取x轴折射角和散射方差的方法,参见图6(b)。
衍射增强成像原理为,一平行X射线束经过两块夹角可调的单晶(图6),放置样品前,探测器可以测得随分析晶体角度变化的摇摆曲线(图7)。当在两块单晶之间放置样品后,样品的吸收、折射和散射便会调制摇摆曲线,通过测量每个像素摇摆曲线下面积减小可知样品的吸收,通过测量每个像素摇摆曲线的角位移可知样品的折射角,通过测量每个像素摇摆曲线的增宽可知样品的散射方差。因为至少采集三次数据才能确定摇摆曲线,所以衍射增强成像至少对样品曝光三次,才能获得吸收、折射和散射三种信息。

图6 衍射增强成像示意图

图7 摇摆曲线
3.2.2 基于光栅的相位衬度成像
2002年,瑞士保罗谢尔研究所C. David[13]等从实验上验证了,利用光栅干涉仪获取物体相位信息的可能性。2003年,日本东京大学A. Momose等[14]提出样品折射调制光栅自成像条纹的成像方法。2006年,瑞士光源F. Pfeiffer等[15]把该方法推广到实验室光源,并于2008年提出样品散射调制光栅自成像条纹的暗场成像方法[16](暗场成像就是散射方差成像)。2009年,中国清华大学黄志峰等[17]提出,样品折射和散射调制光栅投影条纹的成像方法。2010年,中国高能物理所朱佩平等[18]根据样品翻转180°折射角的反对称关系,提出正反像成像方法。
基于光栅的相位衬度成像原理简述如下。参见图8,放置样品前,源光栅每条线源发出的X射线,经过分束光栅都会在分析光栅处产生周期和分析光栅周期相同的条纹(此条纹可能是分束光栅衍射的自成像条纹,也可能是分束光栅的投影条纹),源光栅相邻两条线源产生的两套条纹之间错位一个周期。由此可见,源光栅的作用是比单条线源产生平均光强和对比度更高的条纹。分析光栅沿x轴方向位移时,探测器可以测得随分析光栅位移变化的位移曲线(又称为光栅步进曲线),参见图9。在分束光栅前放置样品后,样品的吸收、折射和散射便会调制位移曲线,通过测量每个像素位移曲线平均光强的下降可知样品的吸收,通过测量每个像素位移曲线的角位移可知样品的折射角,通过测量每个像素位移曲线对比度的下降可知样品的散射方差。因为至少采集三次数据才能确定位移曲线,所以基于光栅的相位衬度成像至少对样品曝光三次,才能获得吸收、折射和散射三种信息。

图9 位移曲线
如果用能分辨条纹的高分辨探测器,那么就可以既不用分析光栅,也无须三次曝光,一次曝光就能完成每个像素中的条纹测量,通过条纹光强下降获得样品吸收,通过条纹位移获得样品的折射角,通过条纹对比度下降获得样品的散射方差。
3.2.3 基于散斑的相位衬度成像
2012年,英国钻石光源S. Berujon等[19]利用砂纸产生散斑,首次在同步辐射光源上实现基于散斑的相位衬度成像。2014年,德国慕尼黑理工大学I. Zanette等[20]把基于散斑相位衬度成像推广到实验室X射线源。
基于散斑的相位衬度成像原理和基于光栅的相位衬度成像类似,不同之处在于,条纹可以看作有周期的散斑,而散斑可以看作无周期的条纹。参见图10,放置样品前,X射线经过砂纸在探测器处产生散斑。在砂纸后面放置样品后,样品的吸收、折射和散射便会调制散斑,通过测量每个像素中散斑光强下降可知样品吸收,通过测量每个像素中散斑位移可知样品的折射角,通过测量每个像素中散斑的对比度下降可知样品的散射方差。由此可知,基于散斑的相位衬度成像要求使用高分辨探测器。在数学上,上述求解吸收、折射和散射的过程,可以通过放置样品前后两种散斑之间的相关运算来完成,相关运算的平均值提取吸收,相关运算的极大值提取折射角,相关运算的调制幅度提取散射角方差。
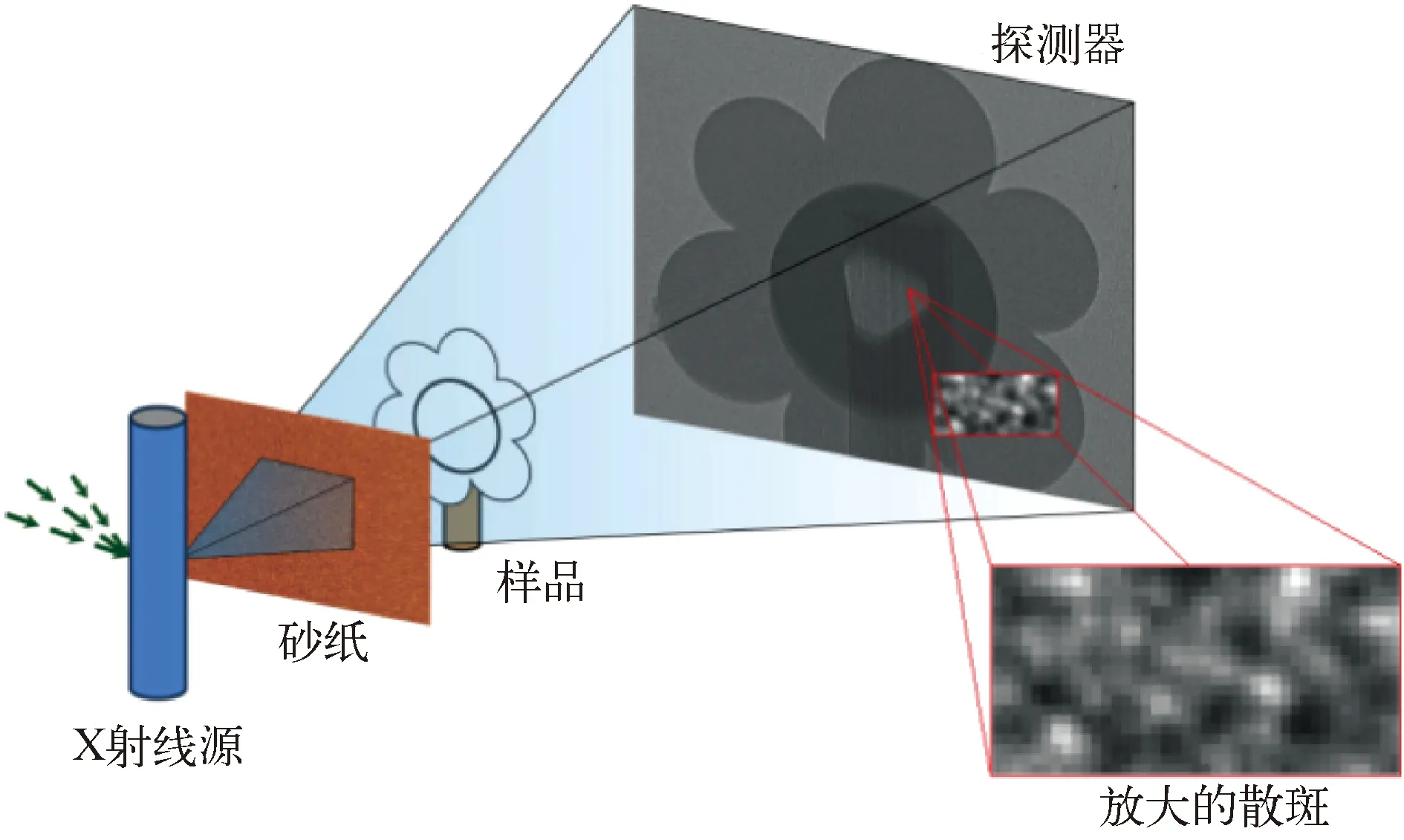
图10 基于散斑的相位衬度成像示意图
3.3 自由传播法
1996年,澳大利亚科学家S.W. Wilkins等[21]和ESRF的科学家P. Cloetens等[22]分别在实验室光源和同步辐射,为自由传播的相位衬度成像发展了衬度传递函数方法(CTF)。同年,澳大利亚科学家K. A. Nugent等[23]提出强度传输方程方法(TIE)。 2002年,荷兰科学家A. V. Bronnikov[24]推导出利用相位二阶导数的CT成像公式。
自由传播相位衬度成像分为两种:一种为微米分辨的同轴相位衬度成像,参见图11;另一种为纳米分辨的同轴全息成像,参见图12。同轴相位衬度成像和同轴全息成像,两者的共同之处在于都有一段自由传播距离;两者不同之处在于,前者只利用菲涅耳衍射的一级条纹,分辨率为微米量级,而后者不仅利用菲涅耳衍射一级条纹,而且利用纳米周期的高级条纹,分辨率为纳米量级。于是产生一个问题,同轴相位衬度成像也利用菲涅耳衍射高级条纹,是否能转换为同轴全息成像?答案是否定的,这里有两种情况需要探讨。首先,同轴相位衬度成像属于投影成像,其分辨率由点扩散函数决定,微米量级的点扩散函数不允许菲涅耳衍射的高级条纹存在。其次,即使点扩散函数达到纳米量级,允许菲涅耳衍射的高级条纹存在,那么不利用菲涅耳衍射的纳米周期高级条纹,也不可能获得纳米分辨的像。同轴相位衬度成像的最初名称是类同轴全息成像,既然是“类”,就意味着不是。同轴全息成像属于衍射成像,其成像过程是先记录由菲涅耳衍射条纹(包括低级和高级条纹)构成的同轴全息图,然后通过同轴全息图中记录的条纹衍射成像,分辨率由同轴全息图中最窄条纹宽度决定。
在同轴相位衬度成像中,参见图11,起主要作用的物理机制是相位二阶导数。其原理为,样品的相位二阶导数可以看作具有聚焦和发散功能的微透镜,当一平面波X射线束经过样品时,平面波变为局部凸凹的波面,出射后经过一段距离传播到探测器,相位二阶导数为负、凸的波面形成局部发散X射线,光强减弱; 相位二阶导数为正、凹的波面形成局部聚焦的X射线,光强增强,由此把相位二阶导数正负分布转变为光强的强弱分布。用探测器把与相位二阶导数有关的光强图像记录下来,就可以重建样品的相位二阶导数。
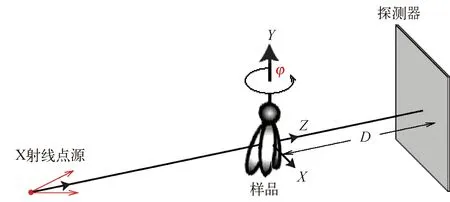
图11 同轴相位衬度成像示意图
同轴全息成像不是一步成像,而是二步成像,第一步记录,第二步重建。探测器记录的不是样品的投影像,而是由样品衍射条纹构成的全息图。以样品中一点为例,参见图12,该点的菲涅耳衍射和平面波在探测器处发生干涉,形成此点的全息图,菲涅耳衍射角θ越大,重建时全息图所拥有的数值孔径就越大,重建像的分辨率也越高。在图12中,图右边是一个样品点的全息图,全息图的最外环条纹宽度决定重建样品点的分辨率。

图12 一个样品点同轴全息图的形成示意图
3.4 微束追踪法
2015年,英国伦敦大学F. Vittoria等[25]提出,基于吸收掩膜的一维微束追踪成像方法,参见图13。2020年,丹麦哥本哈根大学波尔研究所Erik S. Dreier等[26]利用可以感知光子位置的光子计数探测器把一维微束追踪拓展为二维微束追踪,参见图14,完善了微束追踪成像方法。微束追踪相位衬度成像的原理为,利用微束阵列照射样品,样品会对每一微束产生衰减、折射和散射,利用探测器同时、独立、直接测量每一微束的衰减、折射和散射,一次曝光就能获得样品的吸收像、折射像和散射像。

图13 一维微束追踪相位衬度成像示意图
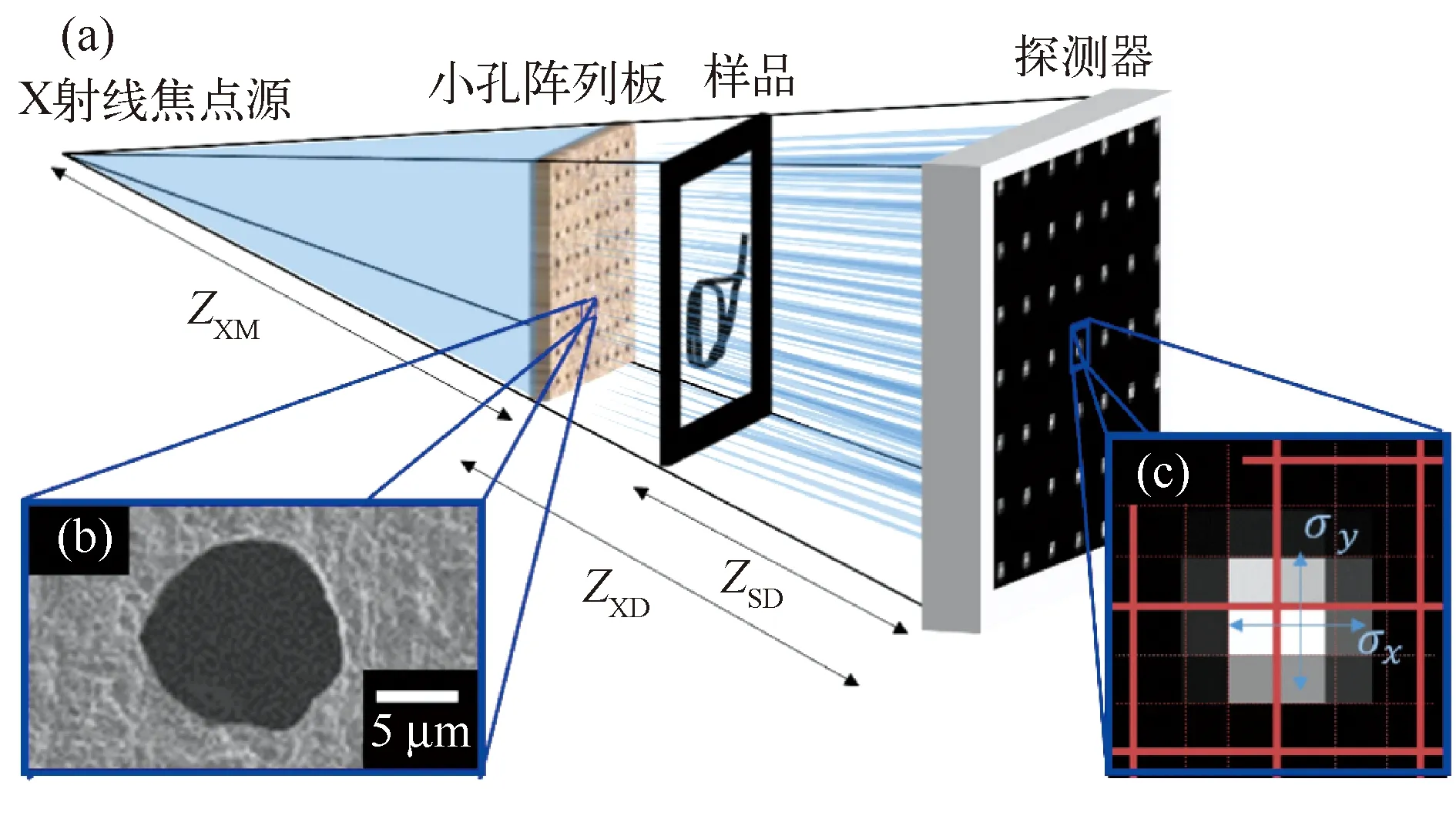
图14 二维微束追踪相位衬度成像示意图
微束追踪相位衬度成像的思想源头可以追溯到,2007年,英国伦敦大学A. Olivo等[27]提出,编码孔径成像方法;2014年[28],提出边缘照明成像方法。从中可以看出,微束追踪相位衬度成像的演化形成过程:第一步,利用第一吸收掩膜形成微束阵列;第二步,撤销显著增加辐射剂量的第二吸收掩膜;第三步,用探测器直接测量每一微束的吸收、折射和散射。编码孔径成像方法和边缘照明成像方法除了是微束追踪相位衬度成像的源头外,还特别容易和基于光栅投影条纹的成像方法[16]相混淆。区分它们的判据在于,是否独立测量每一微束的吸收、折射和散射信息。
3.5 X射线相位衬度成像分类表
综上所述,可以为X射线相位衬度成像建立一个分类表,参见表2。

表2 X射线相位衬度成像分类表
4 国外新方法研究进展
虽然X射线相位衬度成像的分类已经基本包括了目前的所有方法,但是在每个分类中各种新方法仍然层出不穷。下面介绍8个例子,关注的重点在于纳米分辨成像新方法与简便、快速和低剂量的新方法。
4.1 X射线显微镜中加入光栅
为了能在传统的X射线波带片显微镜中看到弱吸收样品,2009年,日本东京大学W. Yashiro等[29]在X射线波带片显微镜中加了一块光栅,经过光栅衍射获得了弱吸收样品(直径5.8 μm的聚苯乙烯小球)的正一级正相位像和负一级负相位像,这是一对孪生像,如图15所示。这种方法的问题是,仅能对少数分布有规律样品排除孪生像干扰,参见图16,对一般样品难以排除孪生像干扰。

图15 X射线波带片显微镜中加了一块光栅的光路图和孪生像结果
4.2 X射线相移点阵显微镜
2010年,瑞士光源Marco Stampanoni等[30]提出X射线相移点阵显微镜,参见图17,从两个方向缩小了相移点侵占的低频空间,减小了低频失真。

图17 X射线相移点阵显微镜示意图
4.3 X射线散射张量CT
2014年,德国慕尼黑理工大学A. Malecki等[31]提出散射张量CT的原理和方法,为样品中每个体素定义了具有K个独立散射矢量的散射张量。换言之,散射张量由K个独立散射矢量构成。实际操作时,常选K=7,或者K=13。为便于想象和理解,图18左图和右图分别描绘出具有7个和13个独立散射方向的分布图。因为散射张量CT要重建的未知量数目是传统CT的K倍,所以必须利用多轴转动或者定点转动,才能采集到足够的投影数据。图19为散射张量CT光路图,样品定点转动,样品散射调制相位光栅产生的条纹载波,分析光栅进行滤波或者解调,探测器采集散射张量的投影数据。散射张量CT没有类似Radon逆变换的直接重建算法,截止目前,都是在离散模型下,利用迭代求解高维线性方程组。在离散模型下,样品被离散为K个体素,共需要采集N×K个投影数据,建立N×K维线性方程组,迭代求解N×K个未知量。图20为散射张量CT重建的碳纤维和牙齿的微观结构取向图[32]。

图18 独立散射方向示意图左图:7个独立散射方向;右图:13个独立散射方向
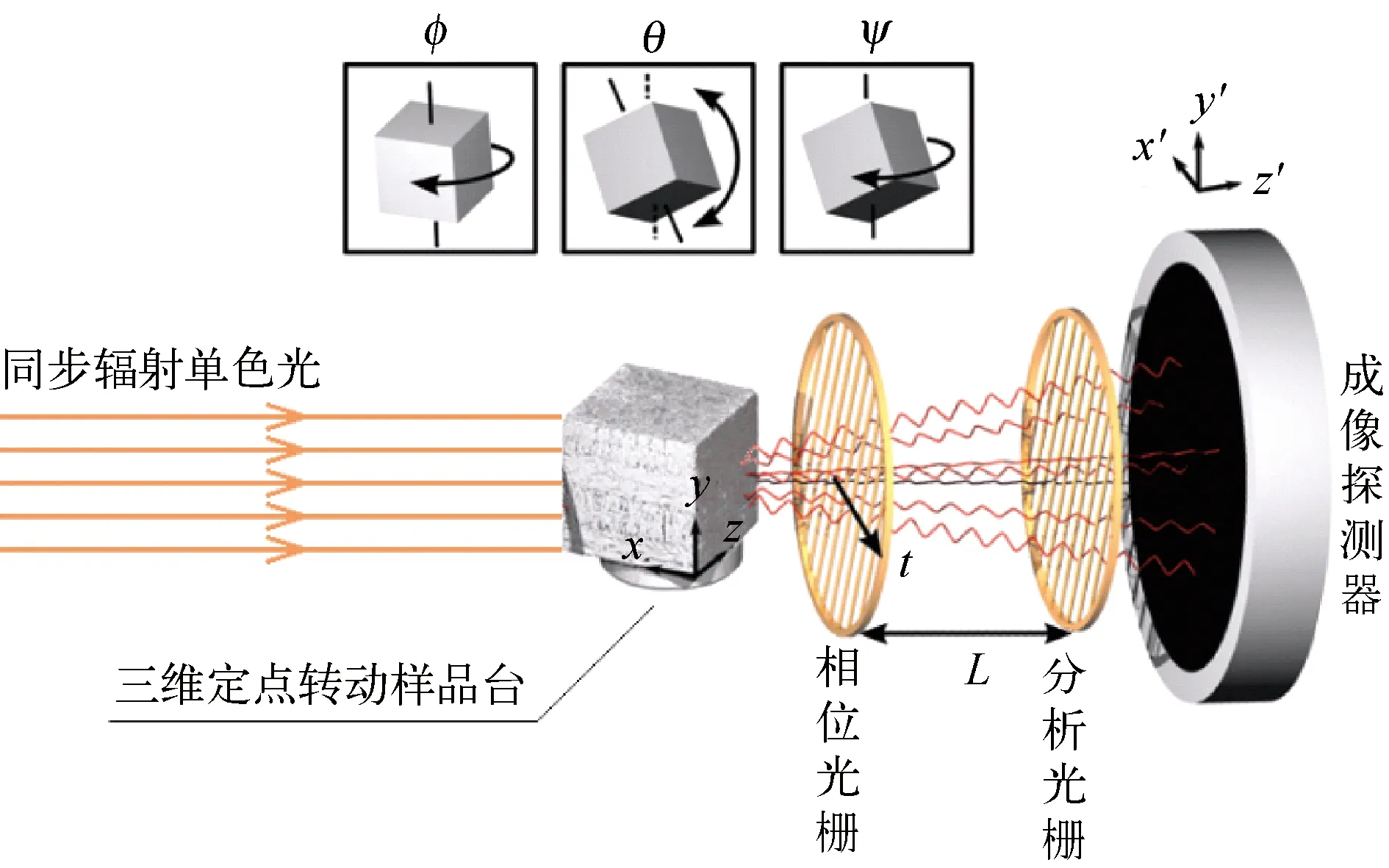
图19 X射线散射张量CT光路示意图

图20 X射线散射张量CT重建的样品中微观结构取向图中图为颜色编码三维取向图,左图和右图分别为重建的碳纤维和牙齿的微观结构取向图。
4.4 基于相位光栅的X射线相位衬度成像
2015年,美国国家卫生研究院Houxun Miao等[33]提出基于相位光栅的相位衬度成像方法,参见图21,消除了吸收光栅衰减光通量增加样品辐射剂量的缺点。
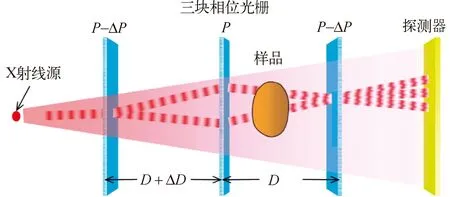
图21 基于相位光栅的X射线相位衬度成像光路示意图
4.5 利用圆光栅单次曝光采集全方向信息
瑞士光源Kagias M等分别在2016年和2019年,利用同步辐射源[34]和实验室源[35],拍摄了载有样品信息的圆光栅条纹和无样品信息的圆光栅条纹,参见图22,通过两幅条纹之间的相关运算,实现单次曝光提取二维折射信息和全向散射信息。

图22 利用圆光栅单次曝光采集全方向信息方法示意图
4.6 利用散斑单次曝光采集全方向信息
2018年,英国钻石光源Tunhe Zhou等[36]分别利用同步辐射源和实验室源拍摄了载有样品调制的散斑和无样品调制的散斑,参见图23,通过插值把每个像素的直角坐标系散斑图转换为极坐标系散斑图,再通过两幅散斑之间的相关运算,实现单次曝光提取二维折射和全向散射信息。

图23 利用散斑单次曝光采集全方向信息方法示意图
4.7 利用微束追踪单次曝光采集全方向信息
在3.4节中已经介绍过微束追踪成像,本节再次提起微束追踪成像,是为了将其和上述两种单次曝光成像方法进行比较。从比较中可以发现,微束追踪成像用探测器同时、独立、直接测量每个微束经过样品后的衰减、位移和扩散信息,用简便快速的方法,获取了最多的成像信息,辐射剂量有望达到最低。
4.8 源和源光栅合二为一的方法
2021年,美国Sigray公司云文兵和昝贵斌等[37]提出把X射线源和源光栅集成为一个X射线栅源,参见图24,消除了源光栅降低光通量利用效率和限制视野的缺点。
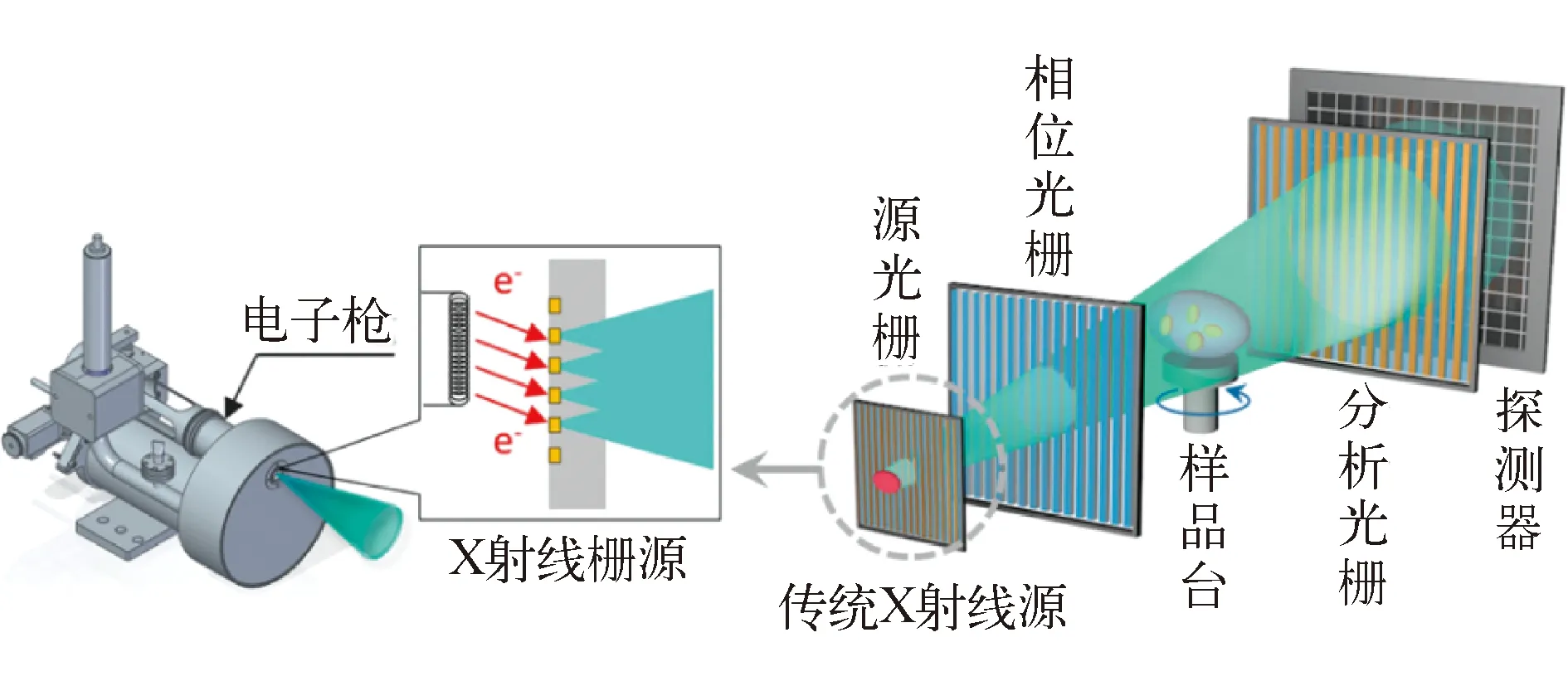
图24 把X射线源和源光栅集成为一个X射线栅源
5 国内新方法研究进展
国内的研究基础落后于西方先进国家,这是一个不争的事实。然而,国内研究已经不限于照搬照抄的跟踪研究,正在出现一些创新的思想萌芽。本文在国内各主要研究单位中,每个单位选一个研究例子进行介绍,从中可以看出国内和国外在研究水平上的差距,需要加倍努力弥补的短板,以及未来有可能赶超的方向。
5.1 基于光栅的相位衬度成像硬件研发进展
在国内,深圳大学郭金川团队[38]研制相位衬度成像硬件能力较强,他们利用自主研制的栅状结构光源、相位光栅和栅状结构探测器搭建了基于光栅的相位衬度成像装置,参见图25。
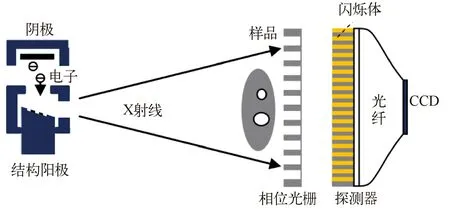
图25 深圳大学自主研制基于光栅的相位衬度成像设备示意图
5.2 利用传播性质消除散斑成像伪影
2017年,上海光源肖体乔团队的王飞翔[39]认为,传统的基于散斑的相位衬度成像公式[19]
I(x,y)=I0exp [-M(x,y)]
(27)
产生伪影的原因是没有考虑透射信号的自由传播,为此提出了修正的成像公式
(28)
并在上海光源做了验证实验,实验光路参见图26,样品为直径为0.6 mm的PMMA小球。验证实验结果表明,修正公式获得了预期的效果,参见图27。

图26 伪影消除验证实验光路图

图27 伪影消除实验结果(a)无砂纸的自由传播像;(b)有砂纸的自由传播像;(c)利用传统公式重建的相位像有伪影;(d)利用修正公式重建的相位像消除了伪影
5.3 建立多阶矩解析方法
2021年,清华大学张丽团队的吴承鹏[40]为基于光栅的相位衬度成像建立了多阶矩解析方法,计算效率相比于传统的多阶矩解卷积方法提高数十倍。多阶矩解析方法的建立过程如下,在基于光栅的相位衬度成像中,有样品位移曲线s(φ)是无样品位移曲线f(φ)和样品散射函数g(φ)的卷积,即
s(φ)=f(φ)*g(φ)
(29)
式中,s(φ)和f(φ)为可测量函数;g(φ)为需要求解的函数。吴承鹏利用傅里叶变换把卷积关系变为乘积关系,有

(30)
并分别把s(φ)、f(φ)和g(φ)的傅里叶级数
(31)
代入式(30),经过推导可把g(φ)用s(φ)和f(φ)表达出来,得
(32)
其中
5.4 相位光栅的虚条纹和虚光源
2021年,中国科学院深圳先进技术研究院的葛永帅团队[40]提出,光栅的自成像是一种类似透镜的聚焦效应,把光栅的自成像距离看为光栅的焦距,于是光源和条纹就成为光栅的物和像,焦距、物距和像距满足透镜成像公式,有
(33)
式中,fi为第i块光栅的自成像距离;li和ri分别为第i块光栅的物距和像距;N为多块相位光栅的数目。根据式(31),可以设计N块相位光栅串联起来的系统,参见图28,其中光栅不仅产生实条纹像,而且产生虚条纹像,前一光栅的虚条纹可以作为后一光栅的虚光源,为多块相位光栅串联系统[32]提出了物理图像清晰,设计思路简捷、适用范围更广的理论。

图28 相位光栅串联系统的虚条纹和虚光源示意图(a)光栅1的实条纹作为光栅2的实光源;(b)光栅1的虚条纹作为光栅2的虚光源
5.5 一条光流线推导出五个投影积分
2021年,北京同步辐射室的朱佩平和何其利[42]认为,X射线从光源经过样品传播到像面上的一个分辨单元,不是一条笔直的、绝对的直线,而是一条具有微小变向的曲线。这条曲线有一根空心管道作为边界,管道始端在光源,始端直径是光源直径,管道终端在探测器像素,终端直径是分辨单元直径,参见图29。根据光流线传播模型和边界条件,可以从一条经过样品的光流线上推导出五个和折射率有关的投影积分,分别是:

图29 一条光流线推导五个投影积分示意图
线性衰减系数的投影积分

(34)
相移项的投影积分
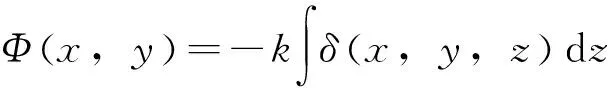
(35)
相移项梯度的投影积分
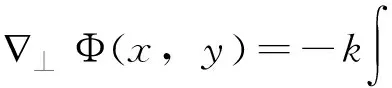
(36)
相移项拉普拉斯的投影积分
(37)
线性扩散系数(相移项随机变化产生)的投影积分
(38)
5.6 微焦点源照射光栅产生连续自成像条纹
2022年,中国科技大学同步辐射国家实验室吴朝等[43]经过模拟发现,在X射线微焦点源照射下,相位光栅的自成像条纹不是离散的,而是连续的,参见图30。经过分析认为原因有三:①相位光栅有吸收光栅的作用,②带宽造成自成像距离偏离理论值,③带宽造成相位光栅相移偏离π/2或π。

图30 光栅自成像条纹连续分布示意图a-e:为在1 μm的钨靶微焦点源照射下,光栅产生的自成像条纹分布图,其中管电压65 kV,输出X射线中心能量40 keV,半高带宽25 keV,光栅材质为金,厚度7.7 μm,周期5.08 μm。f-j:为相应的条纹对比度曲线,其中纵轴为对比度,横轴为相位光栅和分析光栅间的距离,曲线上红星的坐标列在下面,图中R0为光源和相位光栅之间距离,L为光源和分析光栅之间距离。
6 临床前研究进展
临床应用是X射线相位衬度成像研究的美好愿望和不竭动力。人们一直期望着研发出剂量低、衬度高和可应用于临床的X射线相位衬度成像设备。然而,截止目前,研发出的样机,样品辐射剂量都高于传统吸收衬度成像。下面介绍国际上临床前研究最前沿的两个例子。
6.1 乳腺成像临床前研究
2020年,瑞士苏黎世联邦理工大学Carolina Arboleda等[44]研制了基于光栅的乳腺X射线相位衬度成像设备,参见图31,获得了离体乳腺肿瘤样品的吸收像、折射像和散射像,发现肿瘤块和钙化点具有强的散射信号,能提高肿瘤检查的灵敏度,参见图32。存在的问题:①三块光栅之间对准对振动非常敏感,②源光栅和分析光栅是吸收光栅,各自衰减一半入射光子,降低光通量利用效率并增加样品辐射剂量。
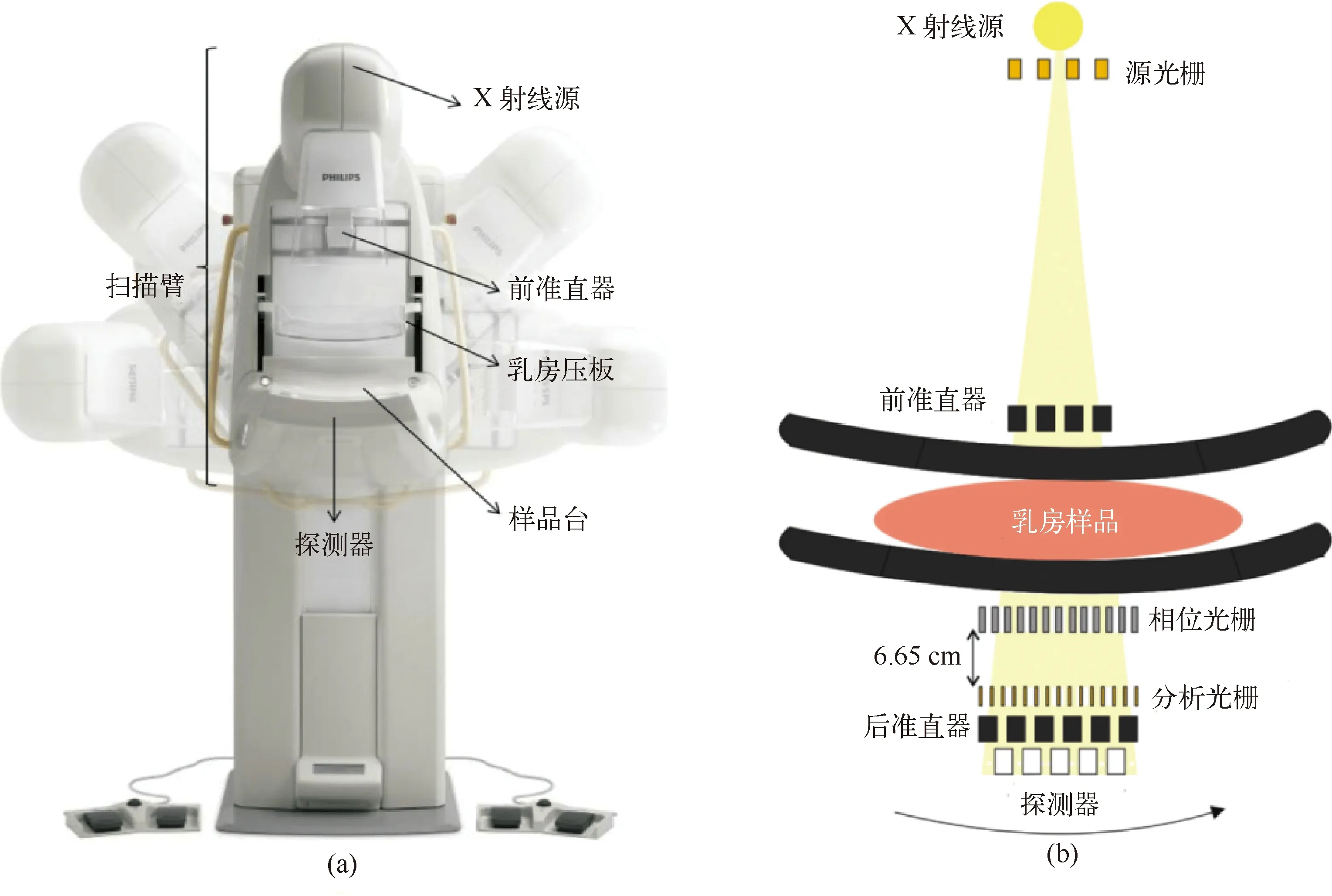
图31 基于光栅的乳腺X射线相位衬度成像设备示意图

图32 离体乳腺肿瘤样品的吸收像、折射像和散射像
肿瘤块和钙化点具有强的散射信号,参见红线围起来的区域和其中的放大图像。
6.2 人体成像临床前研究
2022年,德国慕尼黑理工大学Manuel Viermetz等[45]首次把基于光栅的相位衬度成像机制引入人体医学CT设备,参见图33,获得了人体胸部模体的吸收像和散射像,证明了散射成像机制人体医学CT的可行性。存在的问题,①三块光栅之间对准对振动非常敏感,②源光栅和分析光栅是吸收光栅,各自衰减一半入射光子,降低光通量利用效率,增加样品辐射剂量,③散射重建像的分辨率低于吸收重建像,参见图34。

图33 基于光栅的人体相位衬度成像设备示意图
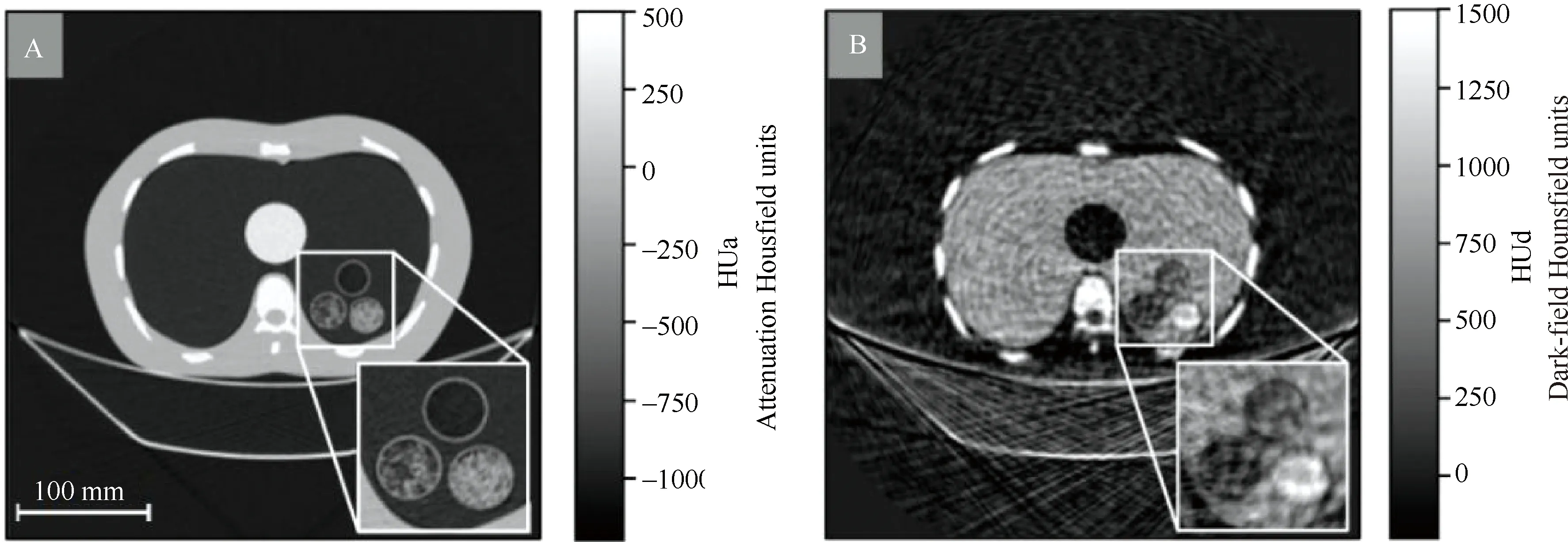
图34 重建的人体胸部模体(A)吸收断层像;(B)散射(暗场)断层像,散射重建像的分辨率低于吸收重建像
7 展望
本文进行三方面的展望,首先是大科学装置中同轴全息纳米CT,其次是X射线相位衬度成像理论创新,最后是X射线相位衬度成像在医学临床的前景。
7.1 同轴全息纳米CT成像
同轴全息纳米CT是目前已经发展成功的X射线相位纳米CT[46]。预计2026年,在北京怀柔建成的高能同步辐射光源,有三条光束线站将建成分辨率达到50 nm的同轴全息纳米CT成像装置,参见图35。这三条光束线站分别是:B-2线站:硬X射线纳米探针[47],B-3线站:结构动力学[48],B-7线站:硬X射线成像[49]。

图35 同轴全息CT光路示意图
7.2 成像理论创新
传统显微镜成像理论,用傍轴平面波传播模型求解,在样品内用投影光线近似计算吸收和相移,在样品外用菲涅耳衍射计算传播结果,根本不考虑样品内部折射。然而,不考虑并不意味着不存在。真实的物理过程是,样品折射改变了出射菲涅耳衍射子波的传播方向,却不改变样品的成像光强,参见图36。可以发现,样品折射在透镜成像中不起作用的原因,图中虚线光锥是传统理论描述的不考虑样品折射的菲涅耳衍射子波,实线光锥是真实的被样品折射的菲涅耳衍射子波。虽然两种菲涅耳衍射子波传播方向不同,但是不影响两者聚焦在相同的像点上。更深入的分析表明,在X射线显微镜成像中,物镜有两个并行的成像过程:一个是样品的放大成像,另一个是照明光环的缩小成像,参见图37。虽然样品折射对自己的成像不起作用,但是会改变光环像的位置。根据这个认识,中国科学院高能物理研究所的朱佩平、洪友丽和张凯在光环像位置加了一个滤波环[50-51],设计了X射线微分相位衬度显微镜原理验证试验,利用样品折射和散射改变光环像位置调制样品放大像的光强,获得了样品的折射像和散射像,参见图38。接下来的问题是,如何建立微分相位衬度显微镜的成像理论?显然,根据傍轴平面波传播模型推导出来的投影光线近似是不考虑折射和散射的。因此,必须采用能描述样品折射和散射的模型,即在样品内应用光流线传播模型,而在样品外仍然采用根据傍轴平面波传播模型推导出来菲涅耳衍射。目前,中国科学院高能物理研究所的朱佩平和中国科学院深圳先进技术研究院的葛永帅正在共同开展相关新理论方面的研究。

图36 样品折射在透镜成像中不起作用示意图图中虚线光锥是传统理论描述的菲涅耳衍射子波,实线光锥是真实的菲涅耳衍射子波。

图37 X射线微分相位衬度显微镜原理验证试验光路示意图

图38 左图、中图和右图分别为二氧化硅小球(直径5 μm)的吸收像、折射像和散射像
7.3 人体相位衬度成像
人们一直期望X射线相位衬度成像能应用于临床医学。虽然临床前期研究已经展现了这种可能性,但是距离低剂量、高衬度和简便快速的目标似乎还很遥远。这使得研究人员经常扪心自问:低剂量、高衬度和简便快速的人体相位衬度成像是否真有希望?正向思维难以开拓前进道路的时候,试试逆向思维提出问题:是否存在一种能和人体吸收衬度成像在剂量、衬度和速度上竞争的人体相位衬度成像方式?
逆向思维可以想到的一个方案:参见图39,如果能想办法形成直径约为40 μm、传播2 m距离不扩散的、空间周期约为100 μm的X射线微束阵列,利用这种微束阵列X射线照射人体,并直接用探测器测量人体对各个微束的吸收衰减、折射和散射,不仅样品辐射剂量低、数据采集速度快,而且可以获得吸收像、二维折射像和全向散射像,信息量成倍增长,那么就能研发出各项指标都优于传统人体吸收衬度成像的人体相位衬度成像设备。

图39 人体X射线相位衬度成像方案
7.4 芯片相干光源
2014年,Reviews of Modern Physics 86卷1380页[52]预言了芯片X射线自由电子激光器。2020年,Science 367卷 79页[53]发表了激光驱动的芯片电子加速器的实验结果。这是产生直径不扩散X射线微束阵列的希望,预示着芯片相干光源将为医学成像带来新的革命。

