异形构件中子CT/CL扫描及重建算法综述
林 强, 罗 涛, 马泽明, 王文健, 丁昊昊, 杨 民
(1. 西南交通大学 牵引动力国家重点实验室 摩擦学研究所, 成都 610031; 2. 西南交通大学 唐山研究院, 唐山 063000; 3. 北京航空航天大学 机械工程及自动化学院, 北京 100191)
0 引言
中子与X射线作为两种重要的辐射源,在材料学、生物医学、航空航天、汽车工业、电子、考古、安检等领域的无损检测中发挥着越来越重要的作用[1-3]。众所周知,X射线、中子与物质作用的机理不同,如图1所示。X射线光子作用于物质原子核外电子,其作用截面与核素的原子序数有较为确定的函数关系,高原子序数的物质具有较大的X射线作用截面,从而使得高原子序数的物质在X射线图像中具有较高的对比度;而中子则不同,其直接与原子核相互作用,散射截面大小与原子序数无关,同一能量的中子对于不同核素的散射截面也存在较大的差异。尤其是氢元素,在X射线照相中几乎是“透明”状态,而在中子图像上则表现为较高的对比度。可见,中子与X射线成像特性存在着很好的互补性:X射线在检测金属材料、高密度物质时则具有更高的灵敏度,而中子成像在检测含较轻元素(氢、锂、硼等)的材料、原子序数相近元素、同位素、放射性材料等方,面有着X射线无法具备的优势[4-6]。

图1 X射线、中子与物质作用的机理[1](a)中子;(b)X射线;(c)散射截面大小
但是随着研究工作的进一步深入,以及日益多样的工程检测需求,基于中子源的CT(Computed Tomography)成像技术面临以下问题:①对于板状、大尺寸筒状构件,如板状和筒状核燃料组件、复合材料板、筒状金属装药容器、板状锂离子电池等,受探测器成像面积和扫描方式的限制,传统的CT扫描无法实现对该类构件的层析检测;②低中子产额、低转换效率导致中子CT扫描周期为几小时至十几小时,无法满足工程检测需求,且增大了样品中子活化的风险。
采用稀疏角度投影CT扫描技术可有效解决扫描时间过长和样品辐照活化问题。在异形构件的层析方法方面,分层层析成像(Computed Laminography, CL)技术及外部CT扫描技术是专用解决板状构件及大尺寸筒状构件的层析成像方法,因此,本文着重从稀疏角度投影中子CT成像方法、中子外部CT扫描技术以及板状构件中子CL层析扫描技术三个方面综述了国内外的研究现状。
1 中子稀疏角度投影CT成像
1.1 中子稀疏角度投影CT成像技术的提出
中子层析成像系统主要实现对待检物体的内部质量与结构信息的无损检测,主要由中子束流、成像装置、运动控制系统、屏蔽装置与上位机系统等部分构成,中子层析成像系统如图2所示[7]。中子成像设备安装在反应堆热柱的水平通道处,该通道相对于反应堆芯呈放射状。中子束从中子孔道中穿出并穿过被检样品,衰减后的中子束到达中子闪烁体转换屏。转换屏通常由荧光物质、中子转换物质和粘合剂组成,中子转换物质吸收中子并与之相互作用,产生α、β、γ射线或反冲物质等,这些带电粒子或次级射线使荧光物质发光,从而产生被检物体投影的光信号。光信号被反射镜引出辐射场,并被CCD相机转换为电信号。为保护CCD相机免受辐射损伤,成像系统一般用铅、硼或锂进行屏蔽。
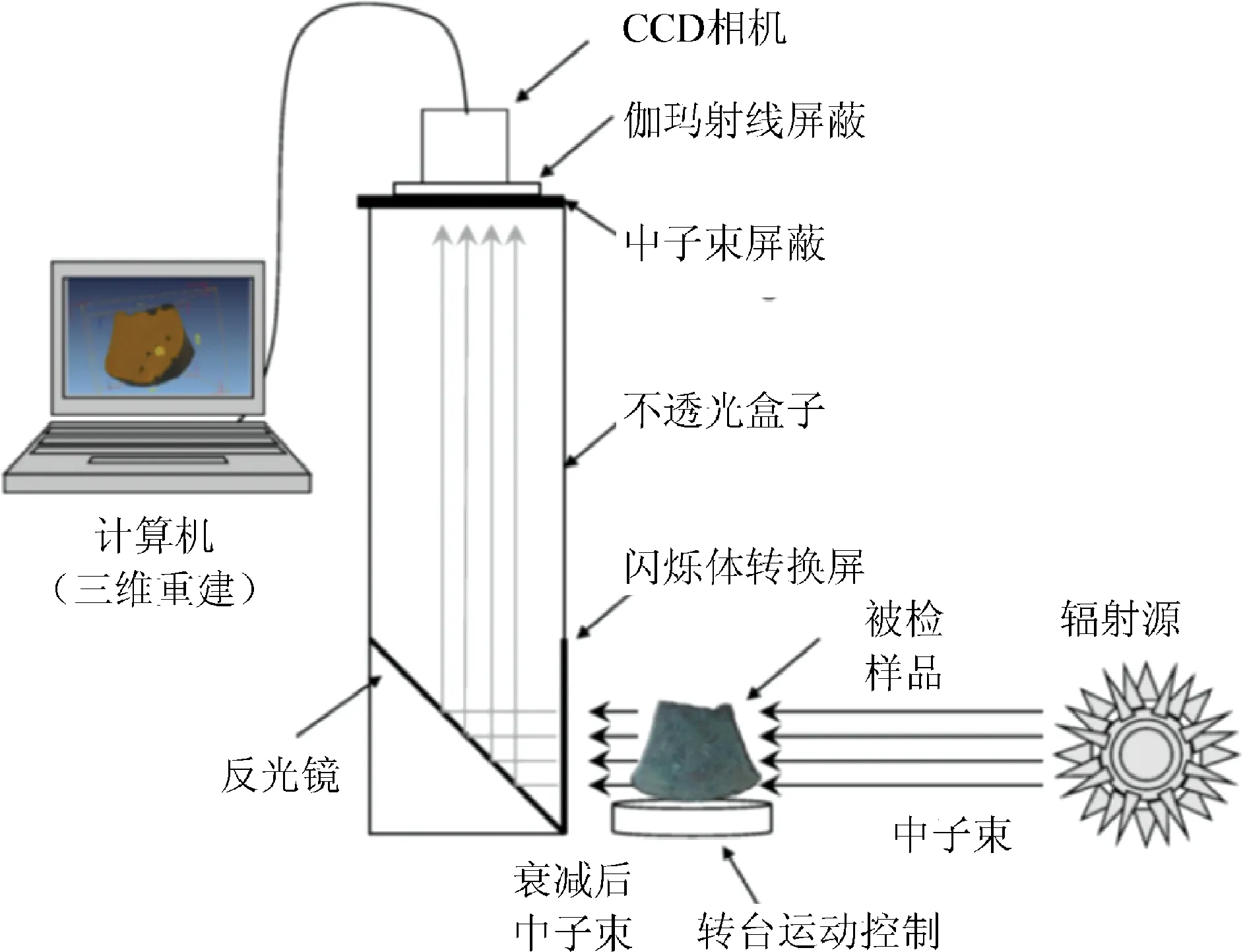
图2 中子层析成像系统[7]
解决扫描时间过长和样品辐照活化问题的有效措施是稀疏角度投影CT扫描。这样就使得投影数减少、投影噪声增加。如何利用较少的投影数据重建出理想的断层图像是CT成像领域里的研究热点。目前,稀疏投影下的图像重建主要有两种解决思路:一是迭代重建算法,如代数重建算法(Algebra Reconstruction Technique, ART)[8]、最大期望(Expectation Maximization, EM)算法[9]、重投影迭代重建算法(Iterative Reconstruction-Reprojection, IRR)[10]等,基于压缩感知理论的迭代重建算法对投影数据量要求变少,在每次迭代重建的基础上可加入不同的先验知识和约束条件,在稀疏投影重建方面具有明显优势。二是随着深度学习、机器学习理论的发展,基于深度学习的重建算法在稀疏投影重建方面具有很大的潜力[11]。
1.2 中子稀疏角度投影迭代重建算法
目前稀疏角度投影迭代重建方面的研究主要集中于X射线领域,典型方法有:2006年,潘晓川等首次将全变差(Total Variation, TV)最小化模型用于CT重建中,被证明是稀疏投影或有限扫描角度条件下改善重建图像质量的有力手段[12]。之后基于TV最小化模型思想的一系列改进算法相继被推出,如2008年Sidky提出的自适应凸集最速下降(Adaptive Steepest Descent-Projection Onto Convex Sets, ASD-POCS)算法[13],该算法2012年被Xiao Han等用于冠状动脉的三维重构中,他们利用9幅投影重构出的三维图像,有效推动了高速、低剂量CT技术的发展[14],如图3所示。2013年张瀚铭等提出了交替方向TV最小化(Alternating Direction Total-variation Minimization, ADTVM)算法[15],较传统滤波反投影重建(Filtering Back Projection, FBP)算法在解决稀疏投影下的图像重建问题具备更大的优势。另外,2011年Vandeghinste提出的基于Split Bregman的ASD-POCS算法[16],以及2014年蔡爱龙等提出的边缘引导TV最小化(Edge Guided Total-variation Minimization, EGTVM)算法[17],属于针对不同应用对象的改进型TV类重建算法。
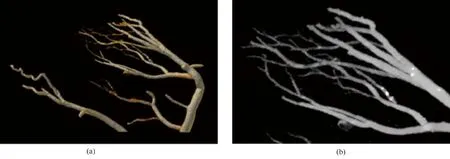
图3 利用9幅投影重建出的冠状动脉三维图像[14](a)三维体视图; (b)最大灰度值视图
而在中子成像领域,有关稀疏投影下的重建技术研究报道相对较少。典型的稀疏角度投影中子层析方法主要有:2016年M Abir等基于热中子源成像装置,采用联合代数重建算法(Simultaneous Algebraic Reconstruction Technique, SART)+全变差最小化算法(Total Variation Minimization, TVM)重建算法,在75幅稀疏投影下重建出了良好的核燃料断层图像[18]。2018年Micieli针对稀疏投影角度下中子束的迭代重建时间较长与解析重建算法图像效果差的问题,提出了一种人工神经网络滤波反投影重建算法(Neural Network Filtered Back-Projection, NN-FBP)。试验结果证明NN-FBP方法在图像质量方面优于FBP和同时迭代重建算法(Simultaneous Iterative Reconstruction Technique, SIRT)。此外,NN-FBP方法的计算复杂度低于SIRT算法,NN-FBP方法的重建时间明显小于SIRT迭代重建时间[19]。2018年Wang针对样品动态变化过程的中子CT检测,提出了一种基于黄金比率扫描策略的稀疏角度SART+TVM重建算法。黄金比率扫描策略能够显著地抑制运动伪影并且能够灵活平衡数据处理期间的空间和时间分辨率。在这种算法中,将足够多的低时间分辨率投影图像的重建结果作为先验图像。采用先验图像约束再通过SART+TVM方法实现对稀疏角度投影数据的迭代重建。实验结果证明,相比于传统的FBP与SIRT迭代重建算法,该算法的时间分辨力与重建图像质量明显提高[20]。为提升高噪声稀疏角度投影条件下中子计算机断层扫描(CT)质量,林强等提出同时迭代重建方法(SIRT)与加权总差分最小化(Weighted Total Difference Minimization, WTDM)相结合的迭代重建方法(SIRT-WTDM)。如图4所示,真实冷中子层析扫描数据验证可知,在极端稀疏角度投影条件下,SIRT-WTDM可获得较好的重建效果[21]。2021年,吴雅朋为提高中子投影图像质量提出了结合SIRT、中值根先验(Median Root Prior, MRP)和WTDM正则化的方法,获得了核燃料元件内部质量检测结果[22]。

图4 编码管样品中子稀疏角度投影重建结果[21](a)编码管样品重建部位;(b)完整数据FBP重建;(c)75幅投影SIRT-WTDM重建
1.3 基于深度学习的稀疏角度投影CT重建算法
近年来,深度学习理论发展迅速,在稀疏角投影CT重建上应用广泛。这种方法由大量数据支持,不受数学或物理模型限制,能够利用训练的深层网络进行良好的层析重建。针对稀疏角CT重建中出现的伪影问题,深度学习方法主要从以下三个方面进行重建和伪影抑制。
第一个方面是在投影域进行处理。Lee等使用卷积神经网络对稀疏角度CT正弦图中缺失的数据进行精确插值,利用ResNet网络获得更好的收敛效果,并且利用网络的Patch-wise训练来避免记忆超载[23]。Lee等在2018年将稀疏角度下的投影数据插值成与完整投影数据相同尺寸的投影,然后利用改进的U-Net网络和ResNet网络中的残差机制,学习插值数据与全角度投影数据之间的映射关系[24],通过网络模型得到合成的投影数据,最后利用传统重建方法完成重建。此类方法虽然简单易行,但投影数据中的噪声对重建结果影响较大。
第二个方面是在图像域进行处理。Xie借鉴GoogleNet中Inception模块多尺寸卷积核的思想,对网络进行改进,利用残差网络和Inception模块提取重构图像伪影特征并进行剔除[25]。Jin等证明了像U-Net这样具有较大感受野的编码器-解码器网络体系结构对消除稀疏角度CT重建条状伪影方面也非常有效[26]。Zhang等将完整角度下重建图像作为标签,将稀疏角下含有伪影的重建图像作为输入,利用U-Net网络学习伪影特征,最后去除伪影获得良好重构结果[27]。Yoseob等指出了U-net网络的局限性,提出了可获得高分辨率重建结果的深度学习网络,并证明了所提出网络能够充分保留稀疏重建图像中的高频边缘细节[28]。Lee等在2020年提出了一种基于多层小波卷积神经网络(Multi-level Wavelet Convolutional Neural Network, MWCNN)的稀疏视图CT重建的方法。该网络架构结合了小波变换和改进的U-net网络,用小波变换代替池化函数,扩大了接受域从而提高性能[29]。不同算法对60幅投影数据重建图像的分辨率对比图如图5所示,文章所提出的方法对图像高频边缘细节保留效果较好。Chen等将自动编码器、反卷积网络和快捷连接结合到残差编解码器卷积神经网络(Residual Encoder-Decoder Convolutional Neural Network, RED-CNN)中,用于低剂量成像研究,该网络在抑制噪声、保存细节等方面取得良好效果[30]。

图5 不同方法对60幅投影数据的重建图像效果对比[29]
由于双域(投影域和图像域)的处理方法极易引入新的伪影和其他人为信息,上述两种重建方法不可避免地会造成一些物体细节特征的丢失,而且这两种方法对数据集的要求十分严格,如果训练数据集太小或不具有代表性,则训练得到的神经网络模型将会受到损害,如果数据集数量过大,则训练得到的神经网络模型可能会产生过拟合问题,所输出结果可能会偏离理想图像。但深度学习相关算法的优势也非常显著,它可以学习比传统迭代重建中使用的正则化函数更加复杂的先验信息。因此,有学者将传统的迭代重建算法展开,利用网络模型学习到的先验信息进行CT重建。第三个方面重建策略是在图像重建过程中结合深度学习的方法,即将每次迭代重建过程展开为深度学习模块。2018年,Chen等提出了LEARN专家网络[31],网络模型框架如图6所示。这种算法将经典的迭代算法展开,将迭代算法中的每一次迭代展开为一个深度学习模块,利用神经网络来学习复杂的正则项和参数,在固定迭代次数中每个模块中不断进行数据拟合更新,此方法在稀疏角度CT重建中取得了显著的效果。由于CT成像中投影域与图像域存在密不可分的联系,因此有些研究工作将二者结合了起来。2018年Zhu等提出了一种图像重建网络框架:通过基于流形近似的自动变换(Automated Transform by Manifold Approximation, AUTOMAP)学习传感器域和图像域之间的重建映射关系,自动映射图像重建的示意图如图7所示[32]。

图6 LEARN专家网络结构[31]
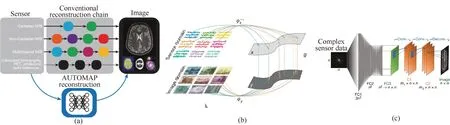
图7 自动映射图像重建的示意图表示[32](a) 传统重建与AUTOMAP重建;(b) 传感器与图像域之间形成映射;(c) 自动映射实现的深度神经网络架构
Wang等在2020年提出了一种完全端到端的深度网络,可以直接将稀疏CT的正弦图映射到CT图像上[33],将FBP/FDK算法纳入深度网络中,避免了训练一个将正弦图转换为CT图像的全连接的层,这样减少了网络的权值数量。该网络用正弦图和CT图像这两个标签进行训练,即使输入的正弦图非常稀疏,也能重建高质量的CT图像。
在中子成像领域,目前应用深度学习方法解决稀疏重建问题的报道较少。2019年,Davide等引入了神经网络滤波反投影(NN-FBP)方法来减少中子成像中所需的时间和投影数据,并证明了NN-FBP能利用更少的投影数据进行重建,所得重建图像质量与标准FBP重建相当,为稀疏投影中子CT成像提供可行方法[34]。
2 中子外部CT扫描技术
2.1 外部CT扫描技术的提出
在大尺寸筒状构件的中子CT检测中,经常会遇到以下三种情况:①感兴趣重构区域(Region of Interest, ROI)为样品的外部区域,如筒内壁包覆层的粘接状态、缺陷、腐蚀等;②探测器长度小于样品直径,无法获取样品的完整投影信息,造成投影数据的截断;③筒状构件内部结构复杂,射线无法穿透筒状样品的内部,而且越靠近样品中心区域,有用的投影信息越少。对于该类构件的CT检测,传统CT不能保证射线束在每个旋转视角下都能包络被检样品,因而无法实现该类构件的断层成像。偏置扫描与第二代CT扫描虽然能够最大限度地扩展成像视野,但由于有限能量射束无法穿透样品的中心区域,导致重建图像质量无法满足精准判读的要求。为了解决上述突出问题,通常只对感兴趣的物体外部环形区域进行CT扫描与图像重建,从而引申出大尺寸筒状样品的外重建问题[35]。中子外部CT扫描原理如图8所示,被检筒状样品在360° CT扫描过程中,中子束与探测器构成的透照场未穿过CT系统转台旋转中心,而且仅覆盖了筒状样品的外部区域,样品ROI重构区域为透照场扫过的环形区[36]。

图8 大尺寸筒状构件中子束外部CT扫描原理(a)大尺寸筒状构件层析遇到的问题;(b) 中子束外部CT扫描[36]
外重建问题的研究开始于医学CT领域,用于实现对心脏外围组织的重建,以减小辐照区域、辐照剂量和心脏跳动带来的重建伪影。目前外重建问题的研究主要集中于重建算法方面,其难点在于,外部CT扫描由于缺失了样品大部分的投影数据,尽管理论上有唯一解,但受投影缺失、图像噪声以及重建模型误差的影响,造成重建图像中样品沿径向的边缘会出现滑坡伪影。Quinto采用计算机仿真的方法验证了外部CT重建图像特点[37],筒状构件的外部CT重建结果如图9所示,图中红色水平实线表示能够采集到的样品投影数据,红色虚线表示缺失的投影数据。奇异点(图像中不连续点、边缘等)A、B处的绿色箭头代表两点奇异性的方向,A点位于重建图像中沿径向处的边缘上,B点位于沿法向处的边缘上。从重建结果可以看出,A点附近的边缘重建结果较好,而B点由于受到投影数据缺失影响,其附近的边缘存在严重滑坡伪影。

图9 外部CT重建结果[37](a)理想图像;(b) 重建结果
2.2 外部CT扫描重建算法
现有的外重建算法主要分为奇异值分解法(Singular Value Decomposition, SVD)、Lambda Tomography(LT)法和迭代重建算法。SVD算法是通过构造正交基将重建图像正交分解,基于已知投影和先验信息分别重建得到相互正交的零空间及其正交补空间,最后将二者合成为最终的重建结果[38]。该方法用级数求和法估计缺失数据,但是由于数学上级数展开有无穷多项,有限项的逼近不能获得精确和稳定的结果,并且缺失数据估计的好坏受原始投影数据的影响较大,尤其对于低信噪比的中子图像,其重建质量和鲁棒性相对更低;LT算法属于局部成像算法的一种,将偏微分方程中Λ算子引入到CT成像,利用求解密度函数的Λ相关函数以获得Λf的分布图像,而非传统的CT值[39];Quinto等在其研究中对LT算法进行了改进,利用有界外推的方法对缺失数据进行补偿,获得了火箭发动机模型的重建结果[40]。
迭代类外重建算法以基于TV最小化算法、子区域平均算法等最为典型。其中心思想为将待重建图像的先验信息转化为约束条件或优化准则,并通过不断迭代的方法获得逼近理想图像的最优解[41]。TVM类算法根据待重建图像的梯度图像具有稀疏性的原理设计重建模型,在重建过程中平衡了重建模型中的保真项与正则化项的关系,迭代获得最优重建结果。Chen等基于锥束X射线CT系统研究了TVM算法对于外重建问题的适用性,结果显示,TVM算法的重建结果优于传统的FBP算法,并具有较好的鲁棒性[42]。TVM类算法虽然对抑制重建图像条状伪影与图像噪声具有明显效果,但对投影数据缺失导致的渐变伪影却无能为力。对此,Shen等提出了一种基于小波紧框架和l0拟范数的外部CT重建算法,实验结果证明,该算法在抑制渐变伪影,提升边缘细节分辨方面更具优势[43]。
带子区域平均化修正的TVM(Subregion Averaged-TVM, SA-TVM)算法由刘宝东等提出[44],由郭雨濛、曾理等发展至外部CT数据重建。其重建过程主要分为三步:第一步为POCS过程,此过程采用SART迭代重建算法获得初始重建结果,并将待重建图像的像素值限制在区间[0,fmax] (fmax是图像数据中的最大值)内;第二步为TVM过程,主要目的是使得重建图像全局全变差变小;第三步为子区域平均化,引入分片常量作为惩罚项,使用活动轮廓(Chan-Vese, C-V)模型将重建图像划分为不同的子区域,将对应子区域内所有像素的灰度平均值作为该区域的像素值。Zeng等将SA-TVM算法应用到扇束外部CT重建中,通过C-V模型识别出灰度均匀的图像区域,然后把该子区域内的灰度值统一为均值,最终重建得到边界清晰的断层图像[45]。随后Guo等将C-V模型推广到锥束以及螺旋束CT重建,并取得较好的伪影校正效果[46]。Guo等将C-V模型改为区域可扩展拟合(Region Scalable Fitting, RSF)模型,设计了RSF-TVM算法,实现了灰度均匀区域的精确识别,数值模拟与实验结果证明该算法在抑制渐变伪影(Gradually Changed Artifacts)和硬化伪影(Beam Hardening Artifacts)方面更胜一筹[47]。在该文献报道中,Guo等采用外部CT扫描方式实现了齿轮样品的层析扫描,不同算法的重建图像如图10所示。图中红色圆圈内的区域为透照场未扫过的区域,而红色方框为感兴趣区域。可以看出FBP算法重建图像具有明显的条状伪影与图像噪声;TVM算法能够有效校正条状伪影与图像噪声,但图像中轮廓细节仍然出现失真情况;RSF-TVM算法重建图像与理想图像最为接近,由于采用RSF图像分割算法的原因,样品轮廓边缘更加锐利,空间分辨率更高。

图10 齿轮样品不同算法的外部CT重建图像[47](a)理想图像;(b)FBP算法;(c)TVM算法;(d)RSF-TVM算法
Guo等在分析外部CT投影数据与重建伪影特点基础上提出了基于加权方向全变差最小化重建算法[48]。该算法是经典TVM算法的借鉴与推广,通过计算待重建点沿径向和切向的离散方向差分,并对其加权求和,最后以加权方向全变差(Weighted Directional Total Variation, WDTV)最小化为目标函数实现外部CT重建,有效抑制了投影数据缺失导致的径向边缘伪影。针对低信噪比、投影数据不完备极端条件下的中子外部CT检测,林强等在WDTV模型基础上,额外增加系列方向组合下的局部方向差分,改进的WDTV模型在重建时均衡了多个不同方向邻域像素的灰度信息,TV最小化的作用得以加强,具有更明显的降噪与抑制径向边缘伪影的性能,该算法齿轮样品重建结果[49],如图11所示。
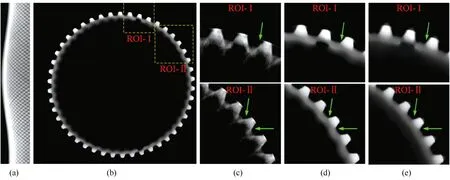
图11 齿轮样品不同重建算法中子外重建图像[49](a)外扫描正弦图;(b) 改进的WDTV模型;(c) SART算法;(d) 所提出模型;(e) 理想图像
文献[50]对SVD分解、Lambda Tomography以及迭代重建算法进行了综合比较,如表1所示,可以看出,外重建问题至今还未得到很好的解决,在针对不同检测对象的算法改进与图像质量提高方面还有很大的空间。另外,外扫描技术的研究主要集中于X射线成像领域。中子图像的信噪比通常较X射线透照图像更低,因此,针对低信噪比中子投影图像的外扫描重建算法改进以及成像几何参数高精度标定算法设计等研究工作有待进一步开展。

表1 外部CT重建算法比较[50]
3 板状构件中子CL层析扫描技术
3.1 CL扫描技术的应用
在工业无损检测中,针对板壳结构,如航天飞机板状超高温陶瓷涂层、板状锂离子电池等,其长、宽尺寸较大,而其厚度仅为几毫米到几十毫米,苛刻的安全性要求和高昂的造价,使其结构形态、缺陷的检测必须依赖于一种有效的无损检测方法。因板状构件长、宽尺寸大、厚度小,传统的工业CT检测手段也会存在以下实际问题:①射线穿过板状物体的最长路径为构件的最大几何尺寸,因此需要射线的能量足够高以穿透物体;②由于穿过的样品尺寸较长,导致射线在贯穿路径最长方向时几乎被全部吸收,难以获得精确重构所需的完备、高灵敏度和高空间分辨率投影,导致重构图像出现“病态”信息。为克服传统的工业CT技术在板壳结构成像检测方面的不足,无损检测领域提出并发展了一种分层层析成像(Computed Laminography, CL)技术。这种技术属于非精确重建算法的一种,通过对构件的不完全扫描,能以高分辨率图像的形式直观地再现板、壳产品内部结构与缺陷。
CL技术的起源可以追溯到经典的X射线分层成像法,该技术由Andre Bocage在1916年提出。经典X射线分层成像法如图12所示[51],X射线源和探测器沿圆周旋转运动或沿相反方向平移,样品内部待重建点的投影坐标会随着X射线源和探测器的相对运动而变化,只有在某个特定平面即焦平面上的点,总能投影在探测器上同一位置,因此,可以清晰成像;而焦平面以外的待重建点总是投影在探测器不同位置,因而这些点无法清晰成像,而是作为背景噪声叠加在焦平面的投影上。因此,经典分层层析成像法存在明显不足:①焦平面以外的断层信息会以背景噪声的形式叠加在最终的图像中,造成分辨率的降低;②每次扫描时,只有一个特定深度的平面得以清晰成像,而其他平面的清晰图像需要通过移动扫描对象进行重复扫描获得。

图12 经典分层成像法原理(a)旋转式分层成像;(b)平移式分层成像
1995年,德国夫琅禾费无损检测技术研究所(IZFP)进一步发展了X射线CL成像技术,采用数字探测器存储一系列不连续投影图像,这一方法克服了经典分层成像法需要多次分层、逐次成像的缺点。中子CL成像时样品旋转轴线与中子束倾斜相交,探测器采集板状样品在360°范围内不同转角下的序列投影图像,通过专用的重建算法,重建出样品的断层结构。图13(b)为旋转型中子CL系统的成像原理,其系统组成与标准中子CT成像系统基本一致。二者的区别在于成像系统的机械装置,这也是CL的优势所在。
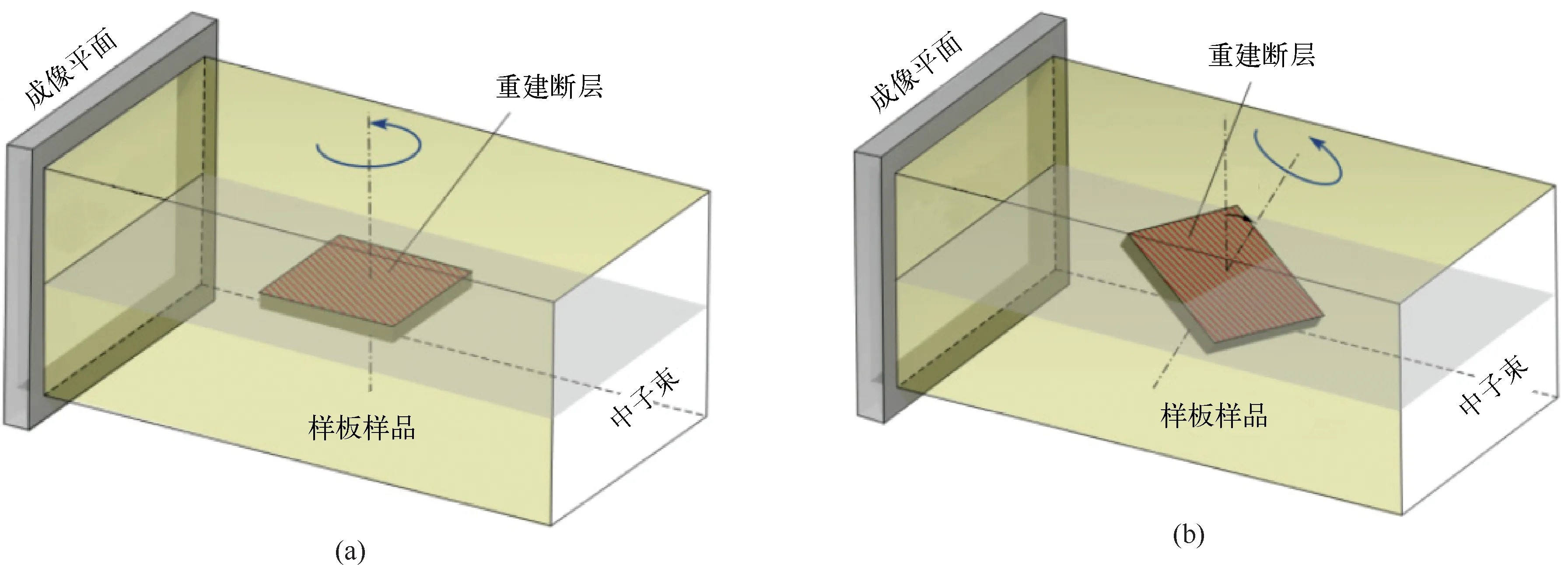
图13 中子CT与CL成像对比[5](a)中子CT层析扫描;(b)CL扫描
目前,CL成像技术在X射线成像中应用研究较多,如Gondrom等基于数字面阵探测器实现了CL成像[52],在微电子芯片BGA缺陷和铝合金焊缝检测方面获得成功应用,极大地释放了CL成像技术的工程应用潜力。此后,X射线CL成像技术在重建算法设计、成像系统搭建及不同领域板状器件的工程检测等方面得到大量研究,如L. Helfen等首次在同步辐射源上实现了CL扫描,获得了高分辨率重建结果[53]。杨民等开发出国内首台CL扫描成像系统,并提出了一系列实用的CL系统成像几何参数标定方法,实现了印刷线路板、板状岩芯样品的CL成像[54-55]。
在中子CL成像方面,美国洛斯阿拉莫斯国家实验室的研究团队基于宇宙射线μ介子被核材料吸收时会诱发散射中子的现象,验证了利用探测到的板状核材料的中子散射投影图像,可以获得样品的内部断层图像,该技术被认为在地下核弹头的探测方面具备应用潜力[56];L. Helfen等在慕尼黑工大的冷中子束线FRM-II上开展了中子CL实验研究,如图14所示,对集成电路板进行层析扫描,获得了布线层的线路分布以及元器件内部低原子序数材料(如塑料)的清晰图像[57]。

图14 中子CL系统成像及层析案例[57](a) CL扫描原理;(b) CL扫描装置;(c) 集成电路板;(d) 三维层析结果;(e)感兴趣区域结果
Filomena Salvemini等在德国HZB同步辐射源的CONRAD II束线上开展了冷中子CL研究[58],并对金属板状古董进行了层析扫描,样品中的腐蚀及存留焊料得以再现;Anders P. Kaestner等在瑞士保罗谢勒研究所的冷中子束线ICON上开展中子CL实验,其目的是面向薄板类艺术品(如钱币、绘画等)进行内部结构成像[59]。Venkatakrishnan SV等在美国橡树岭国家实验室上开展中子CL实验研究[60],对铬钴合金金属构件进行CL重建,获得了高噪声下较高质量重建结果。丰田中央研发实验室团队在日本原子能机构J-PARC中心开发了热中子CL成像装置,并将其应用于汽车电力电子模块内部微观结构无损可视化方面[61-62],对热疲劳循环下双面散热器功率模块内部结构进行了三维可视化分析。Rudolph-Mohr, Nicole等在德国柏林亥姆霍兹材料与能源中心开展中子CL成像研究[63-64],如图15所示,获得了矩形视野内生长的玉米植株3D根系结构,为系统性研究植物根茎生长的动态过程提供相应基础。

图15 Rudolph-Mohr等研制的中子CL扫描装置及检测结果[63](a)CL扫描装置;(b)三维层析结果
3.2 CL扫描重建算法
在CL成像技术的工程应用中,由于CL扫描属于欠完备投影数据下的CT重建问题,重建算法性能对于CL成像质量具有十分重要的意义。因此,CL重建算法的改进与优化成为近几年国内外学者研究的热点问题[65]。
现代CL重建算法主要分为解析重建算法与迭代重建算法。解析重建算法从经典的CT滤波反投影算法中借鉴了许多技术,其特点为重建速度快,是工程中最为常用的重建手段。Myagotin论述了平行束CL的FBP重建算法[66],Gao等在直线扫描轨迹的基础上研究了锥束直线滤波反投影算法(Linear FBP, LFBP)[67];杨民等在锥束圆轨迹CL扫描中实现了一种滤波反投影重建算法(CL-FBP),并应用在电路板检测中[68];傅健等实现了基于圆轨迹扫描和直线轨迹扫描的CL成像,并提出了非对称扫描成像方式[69]和相应解析重建算法[70],扩大了成像视场,提高了成像分辨率;张文提出了基于投影变换的CL层析算法,该算法将CL扫描数据与CL重建几何参数等效转换为到虚拟锥束CT扫描系统中,从而利用现有的锥束(Feldkamp-Davis-Kress, FDK)重建算法进行CL重建[71]。解析重建算法的执行效率一般都很高,但是重建的图像都因数据缺失而存在一定的层间混叠伪影以及图像亮暗不均情况。
与解析重建相比,迭代重建算法的通用性强、重建质量好,在投影数据缺失或者噪声较大时,迭代重建算法的重建结果更优,且无论扫描轨迹多么复杂,都可以通过迭代的方式进行重建。迭代类重建算法自20世纪80年代后期开始应用到CL重建中,近几年随着计算机软、硬件水平的提高,迭代重建算法得到较快的发展[72]。王宏钧、阙介民等分别采用代数重建算法(Algebra Reconstruction Technique, ART)实现了板状构件CL成像[73-74]。常铭等将TV最小化模型与轮廓边界约束思想应用到CL重建,数值模拟和实验表明,基于先验信息约束的重建算法可以有效缓解重建图像层间特征混叠问题[75]。
国内近几年对X射线CL成像技术及装置的开发陆续展开,但是在中子成像领域,我国的中子CL成像方法及应用研究工作很少有报道。林强等基于原子能院中国先进研究堆进行了中子CL扫描实验,为了充分利用中子层析成像技术对于板状材料构件的检测优势,在现有中子CT成像装置基础上,安装可拆卸的倾斜转台,搭建中子CL成像系统,进行CL扫描重建算法设计、重建图像伪影校正等内容的研究,中子CL成像系统与板状样品层析结果[76],如图16所示。

图16 中子CL成像系统与板状样品层析结果[76](a)中子CL层析扫描成像系统;(b)可拆卸CL扫描装置;(c)闪存盘中子CL层析图像
4 未来的研究方向及发展趋势
目前,国外学者已经在中子稀疏角度投影CT重建、板状构件中子CL成像方面做了大量而深入的工作。国内中子稀疏角度投影CT重建方面的研究起步较晚,研究方法与内容也相对有限,板状构件中子CL成像方面的研究鲜有报道;另外大尺寸筒状构件外部CT扫描重建方法的研究也仅限于X射线层析成像领域,外重建问题还未得到很好的解决。对于中子成像中遇到的外重建问题,由于其应用的特殊性和极端成像条件带来的挑战,目前国内外还未有相关的研究和报道。针对中子探测效率低、成像时间长、层析扫描模式单一和成像质量差的问题,未来的研究方向和发展趋势可以概括为如下三个方向。
(1)中子稀疏角度投影重建算法方面,传统的基于加权全变差最小化的重建策略虽能取得较好重建效果,但重建过程耗时久、工程实用性差的问题依旧严重,未来应对算法进行优化,结合多GPU加速技术,设计在线CT集群系统方案,推动算法的工程实现和应用;而采用深度学习的重建策略普适性较差,其重建过程的可解释性仍待考量,再加上中子投影数据高噪声水平的特点,使得该方法与实际应用还存在一定距离。因此,仍需要根据实际的应用场景、优化设计重建模型,进一步提出更加有效的重建策略。
(2)针对外部CT图像径向边缘伪影与CL图像层间伪影的校正,虽然采用相关迭代重建算法取得了一定校正效果,但重建伪影依然是影响样品质量状态及结构信息准确判读的主要因素,后续应在重建模型中结合更加丰富的先验约束信息,如边界约束、先验图像等,进一步提升重建图像的质量。另外,基于深度学习的图像后处理方法是近年来热度较高的CT图像恢复算法,已经在稀疏角度与有限角度CT成像中取得成功应用。后续可针对外部CT与CL重建图像伪影的特点,设计合适的深度学习模型,进一步改善重建图像质量。
(3)对于中子层析扫描,若想取得较好的重建效果其层析扫描时间可达几小时甚至几十小时。对于异形构件的中子CL扫描及中子外部CT扫描适当降低扫描时间,减小样品中子辐照活化风险也是需要重点考虑的问题。因此,稀疏投影CL扫描及外部CT扫描方式下,极端缺失的投影数据必将进一步使得重构图像质量退化。所以,稀疏条件下的外重建及CL层析重建算法优化设计也是国内外学者需要重点关注的研究方向。
邱佩璋先生是我国CT成像领域的开创者之一,为推动我国CT理论与应用技术的发展做出了重大贡献。谨以此文纪念邱佩璋先生!

