有限角CT成像研究进展
赵云松, 李宏伟, 张 朋
(1. 首都师范大学 数学科学学院, 北京 100048; 2. 首都师范大学 北京高等学校检测成像工程研究中心, 北京 100048)
0 引言
X射线CT能够无损地呈现被成像样品内部的三维结构[1-3],自20世纪70年代被发明以来,在医学(组织器官、生理代谢过程成像)、药学(药效检测、新药开发)、材料学(新材料的开发)、工业(各种器件的质检和探伤)、农业(木材和种子的质检和分析)、工程(建筑材料内部孔隙度、连通度和渗透性分析)、珠宝(真伪识别和最佳切割方案设计)、考古(化石的结构和成分分析)等领域发挥了重要的作用[4]。随着CT软、硬件技术的进步,其应用范围也越来越广泛。为此,X射线CT被列为20世纪的十大发明之一。
X射线CT成像即由投影重建图像,通过采集被成像样品不同角度的投影数据,利用特定的成像算法由投影数据重建出被成像样品线性衰减系数分布的图像[5]。理论上,对于一般样品要想精确重建图像,获得的投影数据需要满足数据完备性条件。在探测器尺寸足够大的假设下,Smith指出:被扫描样品能够由锥束CT扫描数据精确重建的充分必要条件是“与被扫描样品相交的每个平面,都与射线源的轨迹有交点”[6]。因此,为获得完备的投影数据,就要在实际CT扫描中,对射线源的扫描轨迹进行适当的设计。但是在一些实际应用中,由于出于对患者扫描剂量的考虑,或是由于样品本身以及CT系统的限制,有时候并不能得到完备的投影数据。这种由于扫描角度限制导致的数据不完备,我们称为有限角数据;相应的成像问题,称为有限角CT成像问题。此外,实际CT系统的探测器尺寸总是有限的。有限的探测器尺寸也可能会导致被扫描样品中一些点沿特定方向的扫描数据不能采集到,从而导致有限角CT成像问题,如外问题[7]。
典型的有限角CT扫描有:①圆轨迹锥束扫描[8-9]。如图1(a)所示,射线源的轨迹构成一个平面圆形。该种扫描模式不满足Smith精确重建条件,因为任一平行于射线源轨迹但不与之相交的平面,都不能与射线源轨迹相交。但是该种扫描模式容易实现,在锥角不是特别大的时候能得到较好的重建图像,因此,仍广泛应用于工业CT和显微CT系统中。②Tomosynthesis扫描[10-11]。如图1(b)所示,该种扫描模式广泛应用于乳腺成像和人体全身的层析成像,其扫描角度很少,一般只有十几度或几十度,所以扫描剂量很低,特别适用于对X射线比较敏感的乳腺等部位的成像。③Computed Laminography(CL)扫描[12-13]。仔细对比图1(a)、(c)会发现,从几何上讲CL扫描模式与锥束圆轨迹扫描模式是等价的,只是其锥角更大一些,一般要大于30°。该种扫描模式的突出优点是扫描样品可以充分靠近射线源,获得较大的放大比,适用于平板状样品的高分辨成像。其他一些常用的有限角扫描模式,可参见文献[13-15],本文不再赘述。

图1 典型的有限角CT扫描(a)圆轨迹锥束扫描模式;(b)Tomosynthesis[16];(c)Computed Laminography[17]
由于投影数据不完备,有限角CT成像问题高度病态,采用传统算法重建的图像中会存在严重的有限角伪影,影响CT图像的阅片和判读。但是由于有限角CT成像适用于一些特定而重要的应用场景,该问题还是得到了国内外学者广泛的研究。本文首先简要介绍了有限角CT图像伪影的特点;然后重点综述了过去近50年间有限角CT图像重建算法的研究进展,包括作者所在团队所做的相关研究和探索;最后概述了目前存在的问题,以及对进一步研究的展望。鉴于作者水平所限,加之时间仓促,综述中难免有疏漏的地方,引文也不可能面面俱到。因此,欢迎读者批评指正,并与我们探讨和交流。
1 有限角CT成像算法综述
有限角重建一直是CT成像领域的难点问题之一,其研究可以追溯到20世纪70年代。在国内外学者的持续努力下,有限角重建的研究不断取得进展。近年来,随着非凸优化及深度学习等方法和技术的兴起,有限角重建的研究被提升到了一个新的高度。
改善有限角重建质量的基本思想是尽可能地挖掘和利用先验信息,并整合到重建模型和算法中。本节首先介绍有限角CT图像的伪影特点,然后综述有限角CT成像算法,包括数据插值方法、正则化方法,以及近年来热点研究的深度学习方法。
1.1 有限角CT图像伪影
1977年,Smith采用奇异值分解方法研究了有限角CT成像问题解的唯一性和稳定性,证明了在一定条件下有限角CT成像问题的解是唯一的,但该问题高度病态,尤其是当扫描角度范围小于120度时,病态程度会随着扫描角度范围的减小逐渐呈指数增长[18]。
基于传统方法重建的有限角CT图像会出现固有伪影。1986—1988年,Louis、Quinto等[19-20]学者证明了沿着与射线垂直的方向,图像的边界较难重建。沿着这一思路,Quinto等于2015年基于微局部分析(microlocal analysis)理论提出了“可见边界(visible boundaries)与不可见边界(invisible boundaries)”的重要概念,并对有限角重建投影数据与重建图像之间的关系进行了深入刻画[21]。根据可见边界与不可见边界的特点,应用传统重建算法(如FBP[22],SART[23]等)重建的有限角CT图像中,沿着与射线相切方向的图像(被扫描样品)边界是可见的;而沿着与缺失射线相切方向的图像边界是不可见的。此外,他们的分析表明,重建的图像还会出现条状伪影(streaks artifacts),且这些伪影都分布在与初始和结束扫描角度相平行的方向上。图2(b)为图2(a)所示的矩形模体利用SART方法从120°投影数据重建的CT图像,可见图像中没有被扫描角度覆盖的边界出现了模糊现象,尤其是水平边界,已完全消失了。此外,重建的图像上也出现了严重的条状伪影。
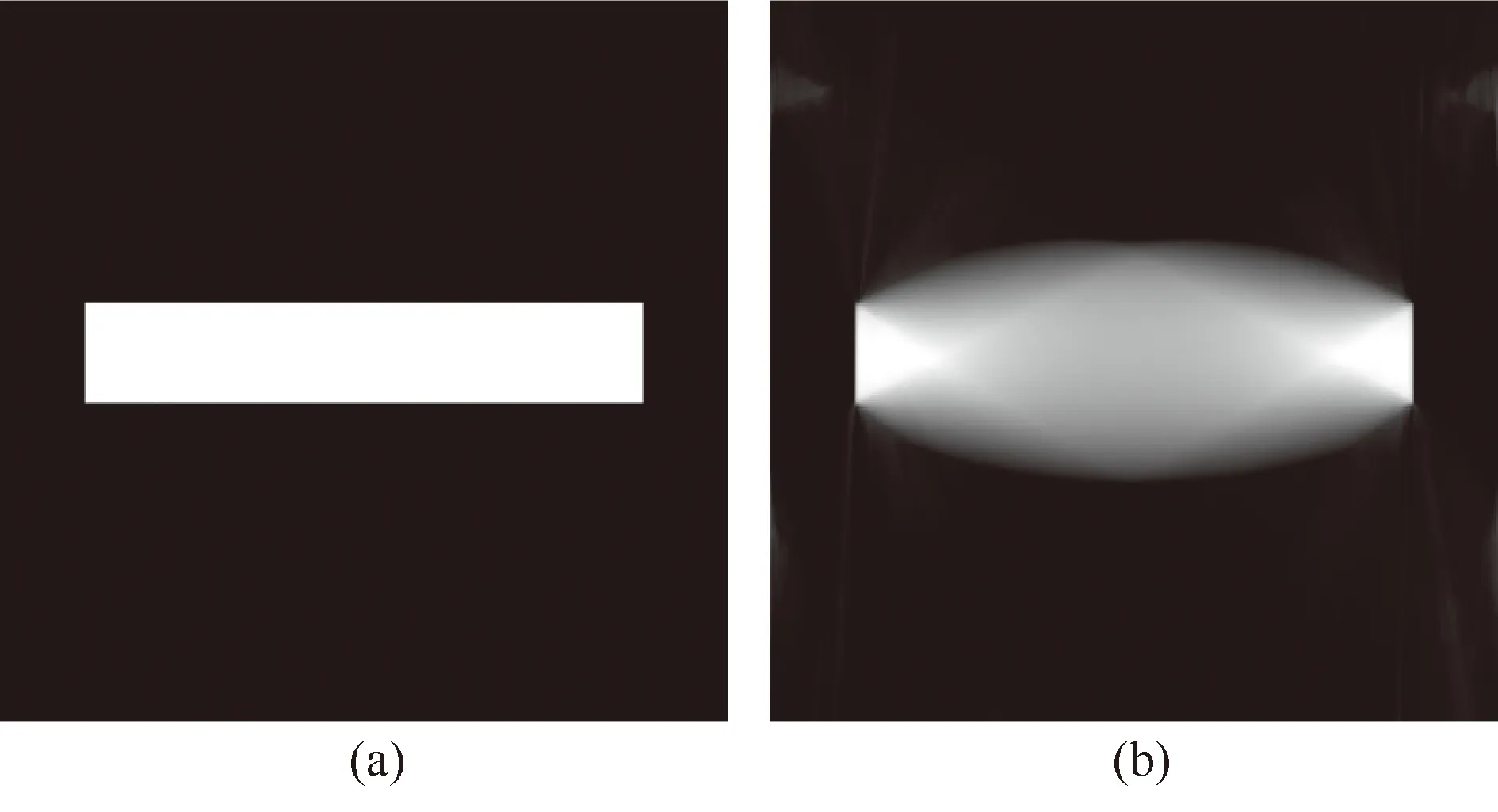
图2 仿真模体及其重建CT图像(a)矩形仿真模体;(b)利用SART方法从120°投影数据重建矩形模体(a)的图像
根据可见边界与不可见边界理论:竖直边界有射线与其相切,因而是可见的;而水平边界没有射线与其相切,因而是不可见的。重建图像沿着y方向上出现了严重的模糊现象,同时也出现了沿特定方向分布的条状伪影。
1.2 数据织补方法
数据织补是非常自然的想法,也是文献上最先提出的方法。这类方法主要利用投影数据的两种先验信息:局部光滑性[24]以及H-L一致性[25-26]。采用的挖掘和利用方式主要有解析延拓[27]、贝叶斯估计[28]、变分优化模型[29]等。投影域织补等价于数据“外插”,本身不够稳定。此外,类似于Fourier 频域空间滤波,投影数据的局部改变会在重建图像上产生全局影响。故投影域织补容易导致重建图像产生伪影以及结构信息丢失。近年来,关于投影域织补的研究相对较少。
1.3 正则化方法
正则化方法是近年来研究最多的一类方法。在很多应用领域,CT图像可以用分片常数函数来近似表示,因而在某些变换域,CT图像具有稀疏性。这一先验信息被许多图像域正则化方法加以利用,以设计相应的优化模型和算法。TV(total variation)正则化常被用来表达分片常数图像。2006年,潘晓川教授等将其引入CT图像重建领域,并提出了ASD-POCS算法来求解包含TV正则项的优化模型[30]。2012年,CP(Chambolle-Pock)算法被引入到CT重建中,可求解包含不同形式的正则项及数据项的能量泛函[31]。与TV所采用的梯度变换类似,小波紧框架[32]、曲波变换(curvelet)以及剪切波变换(shearlet)等,也被用来表达稀疏性[33-35]。这些正则项的引入,在一定程度上改善了有限角CT重建图像质量。
各向异性TV(ATV)重建是有限角CT重建的一个重要进展[36]。ATV对传统的各向异性TV做了扩展,除x,y方向外,它还考虑了非坐标轴方向。对于不同方向上的TV,ATV分配不同的权重。可以认为,在一定程度上,ATV利用了可见边界作为先验信息。采用与ATV类似的思想,文献[37]研究了CT重建中的外问题。外问题也可认为是有限角重建问题,只不过在图像不同的位置处,缺失的扫描角度不同而已。故而在图像不同的位置处,可见边界的分布方向也不同。为反映这一特点,文献[37]采用了较为复杂的权重分布方式。
DART是有限角重建的一个典型迭代方法[38]。该方法没有相应的优化模型,但也可理解成在传统的重建算法中,融入了分片常数先验信息。对于分片常数图像来说,所有像素的灰度值限定于取有限个不同的常数。在每一次迭代中,DART包含了两个过程:SART重建(或其他重建方法)以及阈值分割。分割的目的是修正重建的图像为分片常数图像。如果把分割也看成一种变换的话,DART同样也是利用了变换域的稀疏性。TVR-DART[39]是DART的一个扩展算法,取消了DART对于图像灰度级集合已知的假定。采用图像分割的方式来利用先验信息的工作还可见文献[40-41]。
随着非凸优化在图像处理领域的兴起,非凸模型也被应用到CT重建中。其中TVp(0≤p<1)正则项被广泛采用。非凸正则项对于稀疏性的表达要优于凸正则项。对于有限角CT成像,采用TV0代替TV1, 可有效提升有限角重建的图像质量[42-43]。TV0在表达分片常数函数的能力上比TV1更为有效。如在文献[44]中,作者证明了TV0可以精确恢复边界位置和对比度。实验表明,在保边界能力上,TVp(0≤p<1)都比TV1要好。TV的另外一项进展:RTV(reweighted total variation)也被用于有限角重建。通过在迭代中不断的更新TV的权重,RTV逼近一个非凸正则项,因而可以更高效地挖掘图像稀疏性[45-46]。
文献[47]提出了分方向保边扩散和保边光滑的有限角重建模型及算法(AEDS),深入研究了如何充分利用可见边界作为先验信息来提升有限角重建图像的质量,具体参见本文2.1节。采用类似的保边扩散思想,文献[17]提出了EIDR(edge information diffusion-based reconstruction)算法,有效消除了大锥角锥束CT沿z轴方向的模糊,大幅度提升了CL扫描模式下重建图像的质量。2021年,潘晓川教授课题组又进一步发展出了DTV模型[48],能够由很小扫描角度范围的数据重建出理想的CT图像。
此外,还有文献把图像域的先验信息和投影域的先验信息整合到一个优化模型中,通过双域正则化实现重建图像质量的进一步提升[49-50]。
1.4 深度学习方法
除了传统正则化方法外,近年来,深度学习也被应用于CT重建。因为训练用的标签数据通常包含了投影以及相对应的重建图像,故基于深度学习的重建可归类于双域正则化方法。此外,由于采用了非线性激活函数,深度学习重建属于非凸优化范畴。
2016年,王革教授对深度学习重建做了鼓舞人心的展望[51]。国内外众多学者投入到了基于深度学习的CT重建研究中。2018年5月,X射线CT成像领域的国际顶级期刊《IEEE Transactions on Medical Imaging》推出了机器学习重建特刊,进一步推动深度学习重建的研究热潮。深度学习最初只用于图像后处理,与重建过程并无关系[52-54]。最近发展的深度学习重建方法已经与重建过程深度融合[55-57],都采用了“数据驱动+模型驱动”的方式,即通过迭代展开或者Plug-and-play[58]的方式,把设计的重建算法“映射”成深度网络。然后通过大数据训练,最大限度地挖掘投影域和图像域所蕴含的先验信息。更多关于深度学习的有限角重建研究可见文献[59-60]。
2 作者所在团队的相关研究进展
作者所在团队多年来一直从事X射线CT成像理论和应用研究以及CT设备的研发。近几年,在有限角CT成像算法方面也做了初步尝试,取得了一些进展,并在此基础上研发出了应用于板状物分层成像的两类平板CT设备。以下简要介绍本团队的相关研究工作。
2.1 AEDS算法[47]
AEDS是Alternating Edge-preserving Diffusion and Smoothing的缩写,即交替保边扩散和平滑。该算法的突出优点是在考虑待重建图像先验信息的同时,考虑到有限角CT图像中伪影与扫描角度的相关性,因此,能更有效地消除CT图像中的有限角伪影。AEDS算法得到了著名CT专家潘晓川教授的充分肯定,称其团队的DTV模型是在该算法启发下提出的[48]。与AEDS模型[式(1)]不同,DTV模型将图像先验信息显式地表达为两组不等式约束。所以,DTV模型可以看成分方向TV正则化情形下AEDS模型的约束表示形式。采用不等式约束表达先验信息带来的优点是:对一些特定的扫描样品,模型参数更容易确定。关于DTV模型的具体形式和求解算法可参考文献[48]。
AEDS方法的基本思想是基于如下观察:图2(b)展示了矩形模体[图2(a)]利用SART算法由有限角投影数据重建的CT图像,扫描角度为[30°,150°]。从图中可以看到,虽然扫描角度不完全,模体的竖直边界仍然能够较好重建出来,而水平边界未能重建,出现了严重的模糊现象。这与可见边界与不可见边界的理论相符合,是由于获得的投影数据中缺少了图像竖直方向的频率成分。基于这一观察,我们提出通过水平保边扩散利用竖直边界处可靠的像素值恢复内部像素值的方法。但由于忽略了竖直方向上相邻像素间的相关性,水平保边扩散会在重建的CT图像中引入水平的条状伪影。为了消除条状伪影,我们又增加了竖直方向上的保边光滑操作。最后我们得到如下优化模型:
(1)


图3 模拟数据有限角重建结果注:最后一行为AEDS算法重建结果
2.2 EIDR算法[17]
EIDR是Edge Information Diffusion-Based Reconstruction的缩写,是针对CL扫描提出的一种三维图像重建算法。其基本思想与AEDS类似,也是通过重建出的边界信息逐步恢复图像的内部信息;不同之处在于,CL扫描导致的图像模糊是垂直于水平断层的,我们通过在每个断层图像内求解一种保边界扩散方程来恢复图像内非边界处的信息,具体细节请参考文献[17]。我们利用SART算法和EIDR算法重建的一块PCB板的图像,如图4所示。从图中可以看到,SART算法重建的结果中存在严重的层间混叠伪影,导致PCB走线无法看清;而EIDR算法有效消除了数据不完全引起的图像混叠伪影,使得PCB走线清晰可见。但是,EIDR存在与AEDS算法类似的问题,重建的断层图像应该尽量与PCB走线,以及屏蔽层平行。此外,收敛速度慢也限制了该算法的工程应用范围。

图4 CL扫描数据重建结果(a)SART重建结果;(b)EIDR重建结果
可以看到,EIDR算法有效消除了CT图像层间的模糊。
2.3 其他相关工作
针对上述算法优势和不足,作者所在团队从多个角度尝试了改进,主要工作包括以下内容。
针对AEDS算法收敛速度慢的问题,赵树森等提出通过硬阈值方法对重建图像水平方向的导数图像进行截断,然后再利用截断后的导数图像恢复CT图像[61]。具体实施过程中利用了Fourier变换的微分性质,有效提高了计算速度。此外,该方法还综合考虑了投影数据的噪声模型,降低了投影数据中噪声对重建结果的影响。
扫描数据中的噪声会影响AEDS算法重建的效果,为提高算法的稳定性,邓小娟等提出一种以广义收缩算子作为正则化算子的重建方法[62],采用P-shrinkage算子所隐式定义的广义罚函数替换AEDS方法中的l0和l1范数正则化项,更好地平衡保边界能力以及对噪声或伪影的抑制能力,降低重建模型中正则化参数的敏感性;盛文娟等提出一种基于序列正则化的有限角CT图像重建算法[63],将加权方向梯度约束和标准TV约束序列化使用,在协同抑制伪影的同时相互抑制对方产生的负面影响,从而提高重建图像的质量。
AEDS算法对CT图像中的水平边界具有很好的恢复能力,但是对倾斜边界的恢复能力就要弱一些。针对该问题,鲁昕等提出一种广义的TV正则化有限角CT重建算法[64],该算法设计了一种对图像梯度自适应加权的方法,来调整像素值的扩散方向和扩散速度,从而显著改善了AEDS方法对于非垂直或非水平边界不能很好恢复的问题。此外,由于扩散方向更有利于去除有限角伪影,该方法也有更快的收敛速度;薛晓等提出一种曲率约束的有限角CT重建算法[65],通过在正则项中增加曲率项来限制图像内部边界的长度,从而消除已有算法恢复出的图像边界存在锯齿状伪影的问题。该算法对非水平和竖直的边界有较好的恢复效果。
利用神经网络从数据中学习图像特征是目前的一个热点研究方向,作者团队在该方面也做了初步尝试。马根炜等利用卷积神经网络替换AEDS方法中人工构造的正则化项,通过迭代展开的方法构造了一种交替保边扩散、平滑网络结构(AEDSNN)[66],对仿真数据和实际数据均取得了较好的重建效果。
徐金秋等将保边扩散、平滑的思想应用于外问题成像[67]。由于外问题重建CT图像中的图像模糊是沿极角方向的,因此,在外问题图像重建中的保边扩散、平滑操作分别沿极径和极角方向进行。
3 存在问题及进一步研究
随着图像处理领域挖掘和表达先验信息的方式和手段的进步,近几年来有限角成像的理论和算法取得了较大进展。尽管如此,成熟的应用依然不多。传统模型驱动的算法一般需要上千次迭代才能够收敛,难以满足对于实时性要求高的实际应用需求。此外,由于问题的严重病态性,传统模型的重建结果对于模型及其求解算法中的参数有一定的敏感性。深度学习方法应用于实际问题时也存在着标签数据集难以获取和构建的困难,以及深度网络模型的泛化能力不足带来的可靠性困扰。
针对标签数据难以获取的问题,文献上提供了两种思路:其一是采用无监督(弱监督)学习方法,其二是采用生成模型学习不配对数据集的联合分布或者条件概率分布,从而生成配对的训练数据集。N2N(Noise2Noise)[68-69]系列方法展示了无监督学习在图像去噪问题上的优异性能,且Noise2Inverse[70]、Noise2Sim[71]等方法初步表明,N2N方法也可用于CT图像重建。但如何将该思想用于有限角重建依然需要进一步探索。对抗生成网络(GAN)以及变分自动编码器(VAE)是流行的两种生成模型,已有大量应用。此外,Normalizing flow提供了利用深度网络构建生成模型的新途径,Deflow[72]和LUD-VAE[73]展示了采用生成模型构建配对训练数据集并用于图像复原的可能性,文献[74]表明,生成模型可用于低剂量CT图像去噪。但是,利用生成模型构建的数据集与真实数据集之间的匹配度依然难以保证。针对深度网络的泛化能力不足问题,文献上提出了迁移学习、域自适应(Domain adaption)以及域泛化(Domain generalization)方法。但目前这些方法的应用大多还局限于计算机视觉和图像处理领域。
随着人工智能技术的进一步发展,深度学习方法或将为有限角成像研究注入新的活力,促进有限角CT成像技术的广泛应用。
谨以此文缅怀邱佩璋先生逝世一周年。

