基于排队论的眼科病床资源统筹安排

赵玉涵 陈晓红

摘 要：针对医疗资源紧张的现状，设计合理的资源统筹安排方案，具有重要的应用价值。在此背景下，本文对入院原则和病床系统两个因素展开讨论，建立基于排队论的病床资源统筹安排模型，分别给出在病床系统不变情况下，效率高于目前医院常用先到先服务（First Come First Served，FCFS）原则的新入院原则和入院安排表，以及在FCFS原则下，床位增加数量和各科室床位分配比例的统筹方案，以有效利用病床资源并减少患者的等待时间。

关键词：眼科病床安排;排队论;FCFS原则;优化模型

中图分类号：TB 文献标识码：A doi：10.19311/j.cnki.1672-3198.2022.05.082

0 引言

随着我国经济和科技的迅速发展，人民的生活质量得到了极大提升，与此同时，人们对于医疗健康领域的需求也在不断提高。在诸多的医疗资源中，病床作为患者接受服务的直接窗口显得尤为重要。在医疗资源紧张的现状下，大部分医院采取FCFS原则，这导致床位周转率低下且影响患者及时就医。因此，设计合理的方案实现病床资源的统筹安排就具有重要的实际意义。

近年来，排队论作为一门实用理论在工业、交通、医疗等领域有着重要运用。在医疗领域中，基于排隊论建立资源优化模型是目前解决医疗资源统筹安排问题的常见手段之一，比如文献结合排队论、优化模型、仿真及数据实证分析提出病床分配方案，文献应用M/M/1优先级排队模型对新冠肺炎疫情下的儿童康复病床分配提出了解决方案，文献讨论了在M/M/C排队系统下的病床及手术安排模型。以上工作分别运用不同的方法对病床的统筹安排提供了解决思路，得到了不错的效果，但它们仍存在疾病类型单一、评价指标体系不够完善等问题。

针对以上不足，本文采用外伤、青光眼、视网膜疾病、白内障（单眼）和白内障（双眼）5类眼科疾病的患者数据，结合排队论和优化理论，分别以入院原则和病床系统为研究对象，建立两个病床资源统筹安排模型。本文思路如图1所示：

1 问题分析

由已有患者数据可知该医院患者的平均等待入院时间为10.81天，此等待时间较长，因此设计合理的病床资源统筹安排模型，减少患者等待时间，提高病床的周转次数是本文的研究目标。

本文选择六个基本指标组成评价指标体系，用以衡量一个周期（n天）内的模型性能：

（1）病床使用率=1n∑ni=1aibi，ai、bi分别为第i天被占用和开放的病床数;

（2）病床周转次数=出院总人数开放病床数;

（3）平均队列长度=1n∑ni=1Qi，Qi为第i天排队等待入院患者数;

（4）平均等待入院时间=所有患者等待入院天数之和患者数;

（5）平均等待手术时间=所有患者等待手术天数之和患者数;

（6）P=1n∑ni=1OiQi， P为系统的相对通过能力，Oi为第i天出院患者数。

2 模型的建立与求解

为了建立病床资源统筹安排模型，本文做如下假设：

（1）患者数量是无限的，到达过程稳定且相互独立;

（2）各类疾病的治疗周期是平稳的;

（3）医院在每日工作结束后统计当天的患者数据。

为了建模过程中变量的表达方便，对各类疾病进行编号，详见表1：

2.1 基于入院原则优化的统筹安排模型

根据医疗资源实际情况，考虑各类疾病不同的紧急性和实际治疗需求，结合手术室与医生安排，可制定新入院原则下各类疾病的入院优先级表，详见表2：

2.1.1 模型的建立

在病床系统稳定不变的基础上建立优化入院原则的统筹安排模型，给出新入院原则下的入院安排表，希望使系统的相对通过能力P=1n∑nk=1∑5j=1Oj，k∑5j=1Qj，k尽可能大，从而缓解病床资源紧张的问题，其中Oj，k、Qj，k和Ij，k分别表示第k天第j类疾病的出院、排队等待入院和预计安排入院患者数。

该医院目前的状况是可安排床位不足，因此一个周期内入院与出院患者数量一定相等，即：

外伤患者情况紧急，处于第一优先级，所以会在当天被安排入院，即：

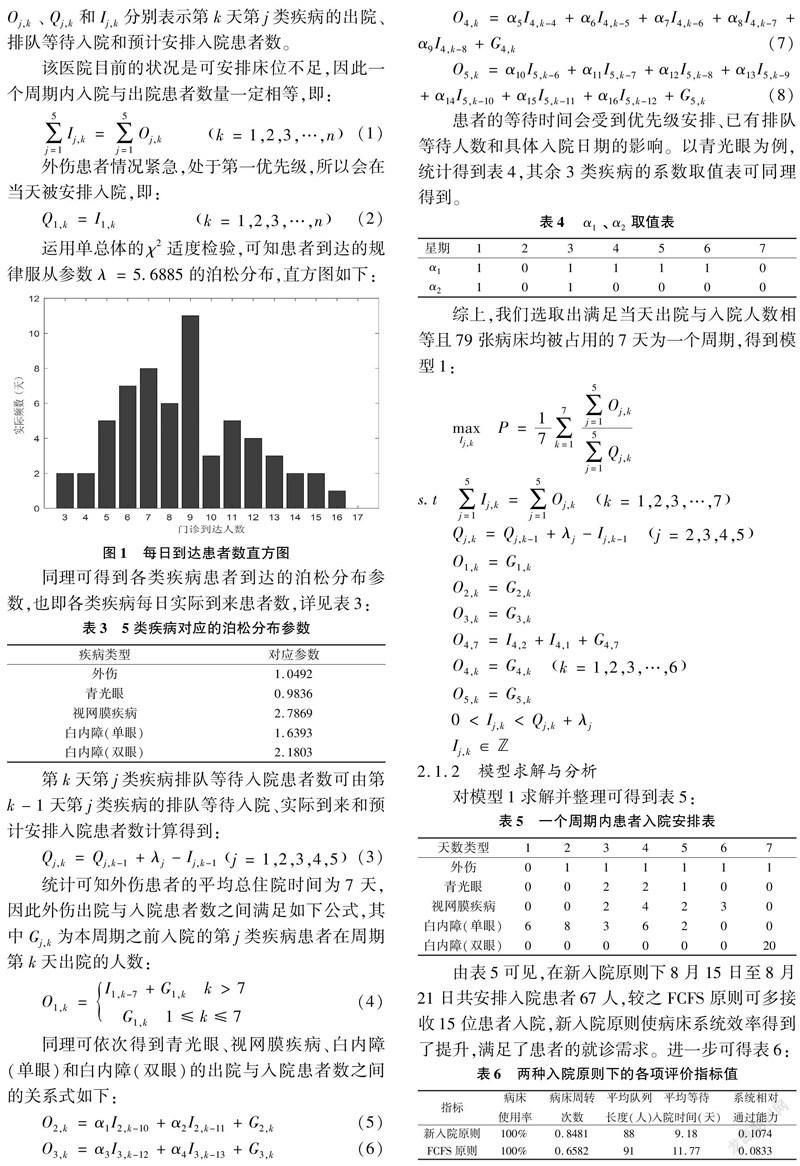
运用单总体的χ2适度检验，可知患者到达的规律服从参数λ=5.6885的泊松分布，直方图如下：

同理可得到各类疾病患者到达的泊松分布参数，也即各类疾病每日实际到来患者数，详见表3：

第k天第j类疾病排队等待入院患者数可由第k-1天第j类疾病的排队等待入院、实际到来和预计安排入院患者数计算得到：

统计可知外伤患者的平均总住院时间为7天，因此外伤出院与入院患者数之间满足如下公式，其中Gj，k为本周期之前入院的第j类疾病患者在周期第k天出院的人数：

同理可依次得到青光眼、视网膜疾病、白内障（单眼）和白内障（双眼）的出院与入院患者数之间的关系式如下：

患者的等待时间会受到优先级安排、已有排队等待人数和具体入院日期的影响。以青光眼为例，统计得到表4，其余3类疾病的系数取值表可同理得到。

综上，我们选取出满足当天出院与入院人数相等且79张病床均被占用的7天为一个周期，得到模型1：

2.1.2 模型求解与分析

对模型1求解并整理可得到表5：

由表5可见，在新入院原则下8月15日至8月21日共安排入院患者67人，较之FCFS原则可多接收15位患者入院，新入院原则使病床系统效率得到了提升，满足了患者的就诊需求。进一步可得表6：

在新入院原则下病床系统的相对通过能力和病床周转次数较之FCFS原则显著提高，而平均队列长度和平均等待入院天数则大幅减少，即有效缓解了排队等待入院患者数与日俱增的困境。

2.2 基于病床系统优化的统筹安排模型

2.2.1 模型的建立

本模型所讨论的病床系统涉及床位数量和分配比例两方面，在FCFS原则的基础上建立基于病床系统优化的统筹安排模型，以维持医院成本、医疗卫生水平和患者逗留时间三者间的平衡。

记第j类患者的平均逗留时间为Tj，平均等待时间为Wj，平均接受服务时间为tj，可得到如下关系式：

病床系统共有N张床位，则第j类患者的病床分配比例ηj和数量Sj分别满足∑5j=1ηj=1和Sj=N×ηj。以第j类疾病为例，患者的到达相互独立且服从参数为λj的泊松分布。病床数量为Sj，每个病床的服务时间相互独立且服从参数为μj的负指数分布。μj即单位时间内被服务的患者数，它与平均接受服务时间tj互为倒数。各类疾病对应的tj如表7所示：

2.2.2 模型求解与分析

对模型2求解可得表8如下：

由表8可知优化后的病床系统拥有93张床位，此时患者在医院的平均逗留时间为12.4896天，相较于原病床系统下的19.7135天，逗留时间大幅减少。计算可知优化前的病床使用率为100%，该指标值过高意味着病床的消毒和维修工作会受到限制，可能导致感染率升高，实际中85%-93%的病床使用率为最佳状态。通过该模型优化后病床使用率维持在86%，兼顾了患者就医体验和医院的整体医疗卫生水平，具有满意的效果。

3 总结与展望

本文立足医疗资源分配紧张的现状，结合排队论和优化模型的理论，针对入院原则和病床系统两个因素，分别建立基于入院原则优化的统筹安排模型和基于病床系统优化的统筹安排模型，为病床资源的统筹安排提供了两种方案。但同时本文也存在一定的局限性，主要体现在缺少医院整体资源的有效数据信息，且未考虑到患者等待过程中的心理因素，我们将在本文基础上继续完善已有模型，考虑更复杂的情况以期得到更加符合实际的方案。

参考文献

[1]王鲁，杨玉中.基于排队论的专项汽修厂维修台配置数量研究[J].数学的实践与认识，2021，51（03）：143-151.

[2]姚入榕，赵德昌.基于排队论的机场出租车最优决策模型[J].现代商贸工业，2020，41（33）：29-32.

[3]刘伟军，邹泽，邱宾，等.基于排队论M/M/C模型的门诊医技排程与医疗设备配置的统筹优化研究[J].中国医疗设备，2020，35（09）：140-143.

[4]Hu J，Hu G，Cai J，et al.Hospital Bed Allocation Strategy Based on Queuing Theory during the COVID-19 Epidemic[J]. Computers， Materials and Continua，2020，66（1）：793-803.

朱桃增.排队论在医院运营管理中的应用研究[D].中国科学技术大学，2019.

[5][6]王平.基于多服务台的负指数分布排队系统在醫院病床分配中的应用[J].现代经济信息，2016，（23）：113.

[7]全国大学生数学建模竞赛.眼科病床的合理安排[EB/OL].http：//www.mcm.edu.cn/html_cn/node/50a7a9fc36c5ce6fd242dbbc1da5878e.html.

[8]蔡文沿.病床使用率和病床周转次数之间的相关性[J].统计与管理，2016，（8）：109-109.

3262500338264