图形在高中数学教学中的应用策略

杨 平

(江苏省连云港市赣榆第一中学 222199)

高中教师在针对学生讲解数学知识时，会涉及到很多的公式、定理等内容，传统教学模式下，教师大量铺陈的做法，已经在实践中被证明不能很好地调动学生的学习积极性，因此对传统教学模式进行适当调整成为必然选择，此时考虑到数学图形的特点与优势，使之在课堂教学工作中展现出独特的魅力，可以让学生顺利完成对抽象数学知识的直观了解与理性认知，最终达到理想的掌握知识与能力构建效果.

1 图形教学的定义

在高中数学教学时，所涉及到的内容可以分成代数和几何两个类别，其中代数知识以抽象的数学符号及数学逻辑为主，而几何知识则侧重于图形规律、特点的直观体现.从本质上分析，这两个类别内容是有着相互联系和相互作用关系的.其中图形作为几何知识中的一种重要表现形式，又可以起到联系代数的桥梁纽带作用.所以很容易概括得到：图形教学定义是借助引入图形的形式，对教学方式进行优化，或者依靠“数”与“形”两相结合的做法，让代数问题以几何图形的形式直观呈现出来，从而帮助师生共同有效解决数学问题，提升知识内化效率.

2 图形教学的价值及原则

2.1 图形教学的价值

在高中数学教学时图形教学的意义非常重要，它既可以有效契合高中数学教学相关要求，又具有以下两方面突出特点，其一是可以帮助做到知识内容化难为易，通常讲，图形教学可以借助图形本身的长处，让抽象知识产生形象化效果，极大地减少学生对于知识的认知难度.其二是可以简化教学过程，改善教学质量，在实践中往往可通过数形结合的形式，破除数学逻辑问题壁垒，对教学过程加以简化.这两方面特点，彰显出图形教学的多项价值.第一，图形教学可以推动理论教学发展；第二，图形教学可以提升习题教学效率；第三，图形教学能够塑造学生数形结合思维.如在面对从含有未知数不等式与等式、含有未知数其他关系式出发，进行某个含有未知数式子的解法时，教师指导学生处理时，如果仅让学生利用代数方法，则很难得到正确答案，若教师能够恰当采取数学图形创新方式，使学生明确函数图像的走向，再使之做到图形和题意的结合，重新分析问题，彰显出图形教学的价值，这对于教师而言，是教学效率提升的保障，对于学生而言，则增加了对于自我能力发展的期许.

2.2 图形教学的原则

图形教学的原则包括如下几点：其一是合理化原则，即俗语所说教学有法而教无定法，不存在任何一种教学方式能够适应所有的教育目标，对于图形教学方法而言同样如此.虽然目前实践证明：将数与形相结合的图形教学方法，能够让大部分函数、代数问题以简单和通俗的形式表现出来，然而若全部问题均以图形教学方法来解答，则极有可能适得其反，让学生因此变得无所适从，不知道如何应对.举例来说，一些数式问题便无法用图形教学来处理，一般同数式有关的问题，极难以图形加以表现，而是要采取深度研究与分析策略才会见到成效，从这个角度上讲，合理化原则是非常有必要的.其二是持久性原则，对于图形教学而言，此方法的应用不能超过它的有效范围，可在其有效范围之内，它的应用是持续有效的，基于其持续有效性，教师与学生可对其应用时间适当延长，使之在更长时间范围内发挥功效，从而利于针对学习内容举一反三、灵活应对，将运用图形变为一种课堂习惯.其三是自主化原则，在高中数学教学期间，所有教学方法的设计均是为了能够提升学生的学习水平，因此教师需要将图形学习法被学生所认知与掌握，使之以高度自主性运用该方法进行分析与解题.

3 图形在高中数学教学中的应用策略

基于图形教学的定义与应用价值，建议教师分别从多个角度，进行图形应用的策略探索.

3.1 概念知识理解角度的应用

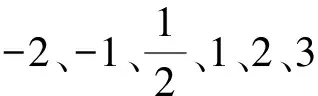
3.2 总结数学规律角度的应用

3.3 知识体系构建角度的应用

因为高中数学学科在难度上是逐渐加大的，同时知识点内容数量极多，这将必然造成学生学习数学知识点的困难.据此，高中数学教师应当有意识地做知识点间的关联性的引导，并利用数学图形的引入策略，帮助学生达到知识体系构建的理想效果.事实证明，借助数学图形能够让学生对于教学活动之中所涉及到的重点和难点内容，拥有更加清晰与直观的认识，同时使之得以最终完成知识点的理性梳理工作，促进系统化知识结构建设结果的达成.例如，在某次高中数学课堂上，教师给学生讲解点、线、面三者之间的关系，一般在此过程中，教师都需要对相当多的数学定理进行重申，如各种性质定理、判断定理等，都要求在学生头脑中形成深刻印象，然而在学生学习期间，由于内容的繁多复杂，他们非常容易把这些定理混淆，从而无法对有关知识较好地掌握.据此，教师采取了把数学图形融入于教学之中的做法，利用数学图形语言描述定理，从而让学生产生了对于基本定理及相关联定理内容的直观与清晰的认识效果.

3.4 简化解题思路角度的应用

高中数学教师有必要充分了解教材内容，同时构建与之相协调的图形结合策略，让抽象数学语言有机会同各类直观图形相结合，用以调动学生形象思维，使之同抽象思维共同被启发和应用，实现数和形间的互相对立及转化变化效果，对简化解题思路起到一定帮助.例如，当涉及到集合的内容时，教师首先要大家明确集合的含义是什么：通常，我们把研究对象视作元素，把元素所构成的整体视作集合，集合内的元素包括下述特征，即确定性、互异性、无序性.教师可以使学生绘制相应的集合图形，在关注到图形特点、图形形式后，把相对复杂的集合及元素，利用图形加以展示.比如可绘制一条封闭曲线，用其内部来代表一个集合，此类图形一般可用来表示无需给具体元素的、比较抽象的集合，而同样的，对于一些给定的具体元素的集合，同样可以用图示法展示出来.像将图形(1 2 3 4 5)与集合{1,2,3,4,5}相联系即是典型示例.教师可再使学生继续运用此种方式，用列举法表示多个集合，像小于十的全部自然数集合，学生便可绘制集合图形，再从图形特点出发，对有关的更具难度的问题加以解决，解题思路将变得清晰简洁.

在图形结合视野下开展高中数学教学，发挥出图形的教学引导功能，这一举措既源于数学教学传统，又具有一定的创新性，然而如何最大化发挥出图形优势，则需要高中数学教师进行深入研究，在充分了解教材内容与图形内容前提下，分别从概念理解、思路简化，以及向形象化方向过渡几个角度，给学生提供其他方法所不能替代的帮助，从而切实提升学生对于数学知识的敏感程度，使其数学思维养成过程更加顺利.