高压大通径井口四通强度分析及流道结构改进

姜玉虎，李龙飞，张学青

（1.江苏宏泰石化机械有限公司，江苏 盐城 224499；2.长江大学机械工程学院，湖北 荆州 434023）

1 前言

四通是石油和天然气开采作业的关键井口设备，被广泛地应用于压裂井口、钻井和采油井口。在钻井或压裂作业过程中，地面管汇与四通采用法兰连接，钻井液及压裂液经四通汇流并注入井下。近年来，国内大力开展非常规油气的勘探和开发，水力压裂规模逐渐扩大，压裂液的压力和排量不断升高，对压裂装备的性能要求也越来越高。

目前，井口四通的关注重点主要集中于四通内腔相贯线处的冲蚀磨损。钟功祥等人采用计算流体力学方法模拟了压裂液物理性质对四通冲蚀规律的影响，结果表明，四通相贯线处管壁存在明显冲蚀。刘鸣等人通过改变压裂液中固相颗粒的粒度、粒径、速度和密度等物理性质预测了压裂四通的冲蚀寿命，其仿真结果同样发现四通相贯线处存在严重的冲蚀。戴义明等人则通过模拟140MPa压力条件下四通流道壁面的压力场和速度场，验证了四通冲蚀位置。王国涛等人基于多相流四通冲蚀试验，建立了稠油热采四通的CFD-DPMEPM冲蚀模型，结果仍表明四通相贯线区域冲蚀严重。王洪亮、侍雁翔等人的研究也表明，钻井用四通的内腔相贯线壁面是重点关注区域。然而，上述研究仅关注了四通相贯线处的冲蚀模型行为，忽略了压裂液高压力诱发的强烈应力集中，同时也未给出合理的改进措施。压裂四通属于含十字相贯腔的厚壁承压容器。相关研究表明，含十字型腔的压力容器的相贯线处存在显著的应力集中，相贯线处壁面材料在高应力状态下，由于力化学效应，壁面金属基体更易腐蚀剥落，加速了冲蚀腐蚀及裂纹的萌生与扩展。因此，需要关注四通内腔相贯线处的应力集中情况。

鉴于此，笔者以江苏宏泰石化机械有限公司研制的5 1/8”105MPa压裂四通为对象，采用有限元方法计算了压裂四通的应力分布情况，并在此基础上提出了四通流道结构改进方案。

2 建立模型

2.1 压裂四通的工作参数和材料性能

压裂四通的设计压力为105MPa，输送介质为压裂液。相关工作参数和结构参数见表1。

表1 结构及工作参数

压裂四通本体制造所应用的材料性能满足ASTM要求，其机械性能如表2所示。

表2 材料机械性能

2.2 实体模型

压裂井口四通为一体式结构，其外形为正方形块，内部设有贯穿的十字型腔。相对采油井口四通和钻井井口四通，管汇连接段与四通完全一体，增强了流道壁面的耐高压能力。其剖面结构如图1所示。

图1 压裂四通三维模型

3 有限元模型

3.1 几何模型

根据圣维南原理，四通端面上用于连接和密封的密封环槽和螺栓孔出的应力对四通相贯线处壁面的应力分布影响极小，因此在建模过程中将上述特征忽略。由于相贯线的存在，会使相贯线处存在显著的应力集中现象。改善相贯线处的几何不连续可以显著减小应力集中，因此，后续分析过程中将相贯线处相互垂直的相贯孔设计为喇叭口型，如图2 b）所示。图中θ为喇叭口的锥度，其变化范围为0°～14°，间隔为1°。

假定四通工作时，只有一个入口和一个出口流通，根据压力四通几何对称性，可以将四通的工况分为以下两种工况：（1）相对侧入口封堵，即入口2和出口开启，入口1和入口3采用盲孔法兰封闭。（2）相邻侧入口封堵，即入口1和出口开启，入口2和入口3采用盲孔法兰封闭。基于上述假设，压力四通的几何模型如图2所示。

图2 四通有限元模型

3.2 网格划分

尽管四通模型在2种工况下几何结构存在差异，但仍满足对称性条件，从计算效率角度考虑，建立1/2模型进行网格划分。四通由于含有相贯腔，结构相对复杂，整体模型采用C3D8R六面体单元划分，整体网格尺寸为13mm，相贯线处避免网格细化处理，网格尺寸为9mm。压裂四通有限元模型由35690个单元组成。

3.3 载荷及边界条件

工况一：四通底部固定，在软件中将底面的所有自由度约束，对称面上施加Z方向的对称约束，内部流道表面施加105MPa介质压力。

工况二：边界条件仍为底部端面固定约束，对称面上设置Z向对称约束，流道表面施加均布内压105MPa。

4 结果与分析

4.1 压裂四通应力分布

图3所示为工况一条件下，相贯线处锥度θ=0°时四通相贯线处壁面的应力分布情况。从图中可以看出：相贯线处壁面上的应力显著高于其他区域，靠近入口2侧相贯线处的应力要显著高于靠近出口侧相贯线处的应力，最大Mises应力为391.6MPa，数值上低于材料的屈服强度。

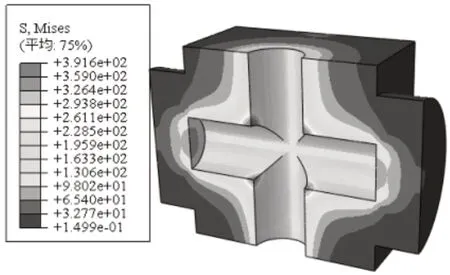
图3 工况一θ=0°条件下应力分布情况

4.2 工况一条件下锥度对相贯线处应力集中的改善

图4所示为流道锥度为θ=10°时的应力分布情况。从云图分布情况容易看出，位于相贯线处的应力仍高于其他区域，应力最大值为359.2MPa，出现在右相贯线上侧中点处，相对于流道锥度θ=0°条件下，其应力值减小了约8.27%，其他流道锥度的分析结果列于表3。

图4 锥度θ=10°应力分布

图5所示为相贯线处最大Mises应力与相贯线处锥度θ的变化规律。结合表3及图5中可知，相贯线处锥度与相贯线处的应力近似呈线性负相关。随着锥度θ的增大，相贯线处的应力值逐渐减小。同时，还发现锥度在10°～12°变化时，应力值的衰减最为剧烈，但之后应力值的变化趋缓。整体看来，四通两侧入口封闭工况下，增大锥度θ能明显地减小内腔相贯线处的应力。但合适的锥度选择还应考虑加工工艺、内壁冲蚀等情况以确定。

表3 两侧封堵情况内腔应力分布

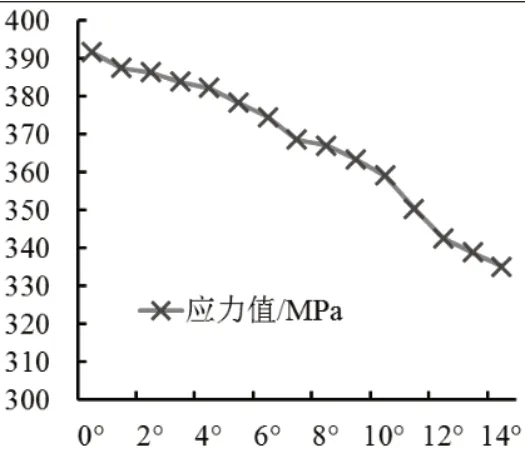
图5 相贯线处应力值随流道锥度变化趋势(105MPa)

4.3 工况二条件下锥度对相贯线处应力集中的改善

图6所示为相邻两侧入口封堵且锥度θ=14°条件下四通内部的应力分布情况。从图中可以看出，相贯线处应力仍高于其他区域，然而，由于几何模型的左右两侧已不再满足对称条件，左右两侧相贯线上的应力存在显著差异，其具体表现为位于左相贯线上的应力值高于右侧。其他流道锥度的分析结果列于表4。

图7所示为工况二条件下的相贯线处最大应力与锥度之间的变化规律。结合表4及图7，可得相贯线处的应力强度与锥度亦呈线性负相关。随着流道锥度的增加，相贯线处应力值逐渐减小。整体看来，当锥度在0～2°时相贯线处的应力对锥度的变化最为敏感。

图6 锥度θ=14°条件下相贯线处应力分布

比较图5和图7，可以发现：锥度θ=0°条件下相邻侧入口封堵时相贯线应力高于相对侧入口封堵工况；增大流道锥度能够显著减小相贯线处的应力；相贯线处的喇叭口设计对相邻侧入口封堵情况具有更显著的四通内腔应力分布及强度改善效果。

表4 相邻侧入口封堵情况内腔应力分布

图7 相贯线处应力值随流道锥度变化趋势(105MPa)

5 结语

以江苏宏泰石化机械有限公司的研制的5 1/8”105MPa压裂四通为对象，基于有限元分析结果，结合相邻侧入口封堵与相对侧入口封堵工况，所得结论如下：

（1）所设计的压裂四通最大应力为396.1MPa，低于材料的屈服强度，满足设计要求。

（2）在传统的直通流道上增加一定锥度的喇叭口可显著改善四通内腔的应力分布情况，减小相贯线处的应力集中程度。

（3）锥度与相贯线处应力近似呈线性负相关。增大锥度，相贯线处的应力可显著降低。

（4）相邻侧封堵工况下增大锥度，相贯线处的应力减小幅度更显著。