基于矩阵分解的船舶交通流预测方法研究
高广旭 刘敬贤 刘 奕 李宗志
(武汉理工大学航运学院1) 武汉 430063) (武汉理工大学内河航运技术湖北省重点实验室2) 武汉 430063)(国家水运安全工程技术研究中心3) 武汉 430063) (伊利诺伊理工大学4) 芝加哥 IL 60616)
0 引 言
船舶交通流是一种非线性的、复杂的时间序列.对船舶交通流预测的研究包括参数法、非参数法和数值模拟三类[1].
参数法主要包括基于灰色理论的预测模型、时间序列方法和卡尔曼滤波等模型.GM(1,1)是灰色模型中最常用的方法之一,由于其运算简单速度快且不需要大量样本,所以在短期预测方面具有很好的应用,但是对于波动性数据的处理并不理想[2].差分自回归移动平均模型(ARIMA)是典型的时间序列方法,对与非平稳数据有较好的处理效果,然而由于交通流数据日变化特性引起了异方差性,使得该模型的残差被低估,会影响预测精度[3-4].由于船舶交通流还具有非线性、随机性及复杂性特征,在对交通流的预测中,参数法无法很好的处理这些特性.非参数法正好弥补了这一缺陷,并且其预测精度更高.在非参数法中,神经网络(NN)是最常用的研究方法之一,并在此基础上发展出多种预测模型[5-6].反向传播神经网络(BPNN)模型,它可以反映出交通流时间序列的分线性特征,能够处理复杂的非线性交通流时间序列,因而被广泛应用于交通流预测中[7].但是由于其同传统神经网络模型一样,具有容易陷入局部极小,收敛慢和易引起震荡等缺点,对预测精度有较大影响[8].面对单一神经网络预测模型在交通流预测中的缺点,有研究学者提出基于船舶交通流不同特性,采用不同的预测模型进行预测[9],避免单一模型对船舶交通流特性考虑不足,提升了船舶交通流预测精度[10-11].随着大数据及数据挖掘技术的发展,通过对船舶交通流大数据进行挖掘,可以发现其内在特征及非线性特性[12],然后提取交通流数据的特征,对每个特征数据进行预测[13].
文中针对船舶交通流的非线性和复杂性提出一种组合预测模型,考虑船舶交通流受不同因素的影响,分析船舶交通流内在特性,将船舶交通流数据看作是由波动性数据和平稳性数据构成的,船舶交通流多是由稳定、周期性数据构成,这一部分数据称之为平稳性数据,当受到突发因素影响而造成的数据波动,称之为波动性数据.由平稳数据构成低秩矩阵,波动性数据构成稀疏矩阵.对于分解后的矩阵采用BPMF模型通过对数据矩阵进行补全的方式进行预测,然后将补全后的矩阵组合得到最后需要的预测结构.
1 船舶交通流预测模型
1.1 船舶交通流特性分析
船舶交通流作为一种时间序列,具有以下特性.
1)在长期时间内表现出一定的周期性,且船舶交通流受到水域内航道、锚地等固定因素的影响,而表现出平稳性特征.
2)船舶交通流在受到自然因素、突发事故等因素的影响,产生一定的波动性.
3)同时在一定周期内,船舶交通流数据还表现出很强的时间相关特性.
4)船舶交通流作为一种时间序列,也体现出一定的空间特性.
因此,考虑船舶交通流的时空属性,将一维船舶交通流数据转为二维交通流数据,并结合交通流平稳性和波动性,对交通流数据进行低秩稀疏矩阵分解,并分别进行预测.进一步提升对船舶交通流的预测精度.
1.2 低秩稀疏矩阵分解模型
结合船舶交通流的时空特性,将一维船舶交通流序列按照日(day)和时间段(time)进行分组转为二维船舶交通流矩M,M∈Rm×n;m,n分别为数据矩阵中行和列,其中行为天,列为时间段,文中按3 h采集一次数据将1 d划分为8个时间段.通过对采集的数据进行相关性分析及奇异值分解,得出船舶交通流统计数据的相关性及低秩性较强,利用低秩稀疏分解是合理的.
对于重新构造的船舶交通流二维矩阵采用低秩稀疏矩阵分解模型对船舶交通流数据进行分解,分解为低秩矩阵L和稀疏矩阵S.交通流矩阵分解步骤如下.
步骤1采集原始船舶交通流一维时间序列数据,并重新构造为二维船舶交通流矩阵M,矩阵M是由交通流稀疏性矩阵L和稀疏矩阵S组成.
M=L+S
(1)
式中:M∈Rm×n为已知的船舶交通流二维矩阵;L∈Rm×n为低秩矩阵;S∈Rm×n为稀疏矩阵.
步骤2为了较好的将交通流矩阵M分解为低秩矩阵和稀疏矩阵,需要对该过程进行约束和优化,并引入正则化参数λ,以平衡矩阵的低秩性和稀疏性.
s.t.M=L+S
(2)
步骤3为了进一步提升公式(1)中S的稀疏性,根据文献[14]研究成果,对分解模型采用非凸优化可以保证矩阵的稀疏性和数值精度,因此基于非凸优化的低秩稀疏矩阵分解模型为
s.t.M=L+S
(3)
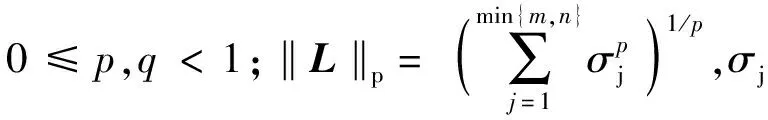
步骤4为了能够得到比较稳定的解,再引入增广拉格朗日乘子Y处理约束非凸优化最小问题.引入该乘子后矩阵分解模型为
(4)
式中:Y为增广拉格朗日乘子;μ为正惩罚参数.利用交替方向乘子算法迭代求解式(3)[15],固定参数L和参数Y求解S,固定参数S和参数Y求解L,再更新拉格朗日乘子Y.
步骤5分别固定参数(S,Y)对L进行求解和固定参数(L,Y)对S进行求解,求解过程为
(5)
1.3 基于贝叶斯概率矩阵分解(BPMF)的AIS预测模型
贝叶斯概率矩阵分解的AIS预测模型是在概率矩阵分解模型的基础上进行优化[16-17],其预测原理主要为矩阵补全,将预测数据看作原始矩阵中缺失元素,通过贝叶斯概率矩阵分解进行矩阵补全以达到预测的目的,在计算中将预测数据在矩阵中以“0”表示,以满足计算要求[18].其预测流程如下.
步骤1将要预测的船舶交通流数据二维矩阵X通过两个矩阵表示,并加入随机噪音矩阵E.
X=HA+E
(6)
式中:X∈Rm×n为包含缺失数据(预测数据)在内的船舶交通流数据;n和m分别为矩阵的行数和列数;H∈Rm×k和A∈Rk×n分别为基函数和对应的系数;k为船舶交通流数据X的秩;E为随机噪音矩阵.
基函数H和相关系数A满足如下的高斯分布:
(7)
式中:Hi:,为基函数H的第i行;A:,j为系数矩阵A的第j列;超参数ΘH={ζH,ΛH}和超参数ΘA={ζA,ΛA}为决定基函数H和系数A分布特征的超参数,这两个超参数都符合Gaussian-Wishart分布.
P(ΘH|Θ0)=N(ξA|ξ0,(β0ΛM)-1)w(ΛH|W0,v0)
(8)
P(ΘA|Θ0)=N(ξA|ξ0,(β0ΛA)-1)w(ΛA|W0,v0)
(9)
步骤2更新超参数ΘH={ζH,ΛH}和超参数ΘA={ζA,ΛA},根据上一步可以得出基函数H和系数A,则超参数的概率密度函数为
P(ξH,ΛH|M,Θ0)=
(10)
P(ξA,ΛA|M,Θ0)=
(11)
步骤3更新基函数H,根据贝叶斯公式:
P(H|X,A,ξH,ΛH)P(X|A,ξH,ΛH)=
P(X|M,A,ξH,ΛH)P(M|A,ξH,ΛH)
(12)
此时船舶交通流数据X,系数矩阵A和超参数都已知,所以概率密度函数是一常数,同时基函数矩阵H和系数矩阵A无关,所以得出基函数H的概率密度函数为
(13)
步骤4更新系数A,和步骤3同理可得:
(14)
步骤5重复步骤2~4直至基函数H和系数A达到稳定输出为止.
1.4 LRSD-BPMF组合预测模型框架
LRSD-BPMF组合预测模型的预测流程见图1.具体步骤如下.
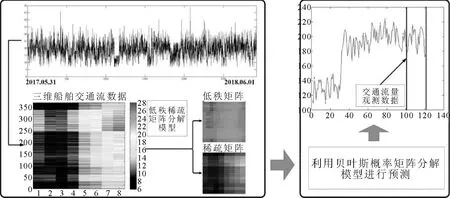
图1 LRSD-BPMF组合预测模型流程图
步骤1数据预处理 将采集的船舶交通流数据进行处理,转换为二维船舶交通流时间序列矩阵M.
步骤2利用LRSD算法,将M分解为低秩矩阵L和稀疏矩阵S,见式(1).
步骤3对于分解后的低秩矩阵L和稀疏矩阵S,分别运用BPMF对两矩阵进行预测值补全,得到包含预测值的低秩矩FL和包含预测值的稀疏矩阵FS.
步骤4将预测后的低秩矩阵和稀疏矩阵恢复为船舶交通流矩阵,即可得到船舶交通流预测结果矩阵FM.
FM=FL+FS
(15)
2 实例分析
2.1 实验数据来源
由于文中提出的预测模型面向的为一般情形下的船舶交通流短时预测,所以对于实验数据的选取没有特定要求.选择曹妃甸港2017年5月31日—2018年6月1日的港口交通流数据,进行验证文章所提出的算法的可行性及有效性.将采集的船舶交通流数据按照3 h为一时间段划分数据,1 d共分为8个时间段,对交通流预测模型进行训练,并将最后8组作为测试数据实验数据来验证模型效果.为了考虑到预测数结果的随机性,提高预测结果的鲁棒性,实验将每个时间段进行10次预测,获取10组预测值.
2.2 预测结果分析
为了验证提出的LRSD-BPMF模型的预测结果精度,实验选取了GM,ARIMA,BPNN,WNN,LSTM,BPMF共六种常用的且预测精度较好的模型进行对比,各模型预测结果统计见图2.
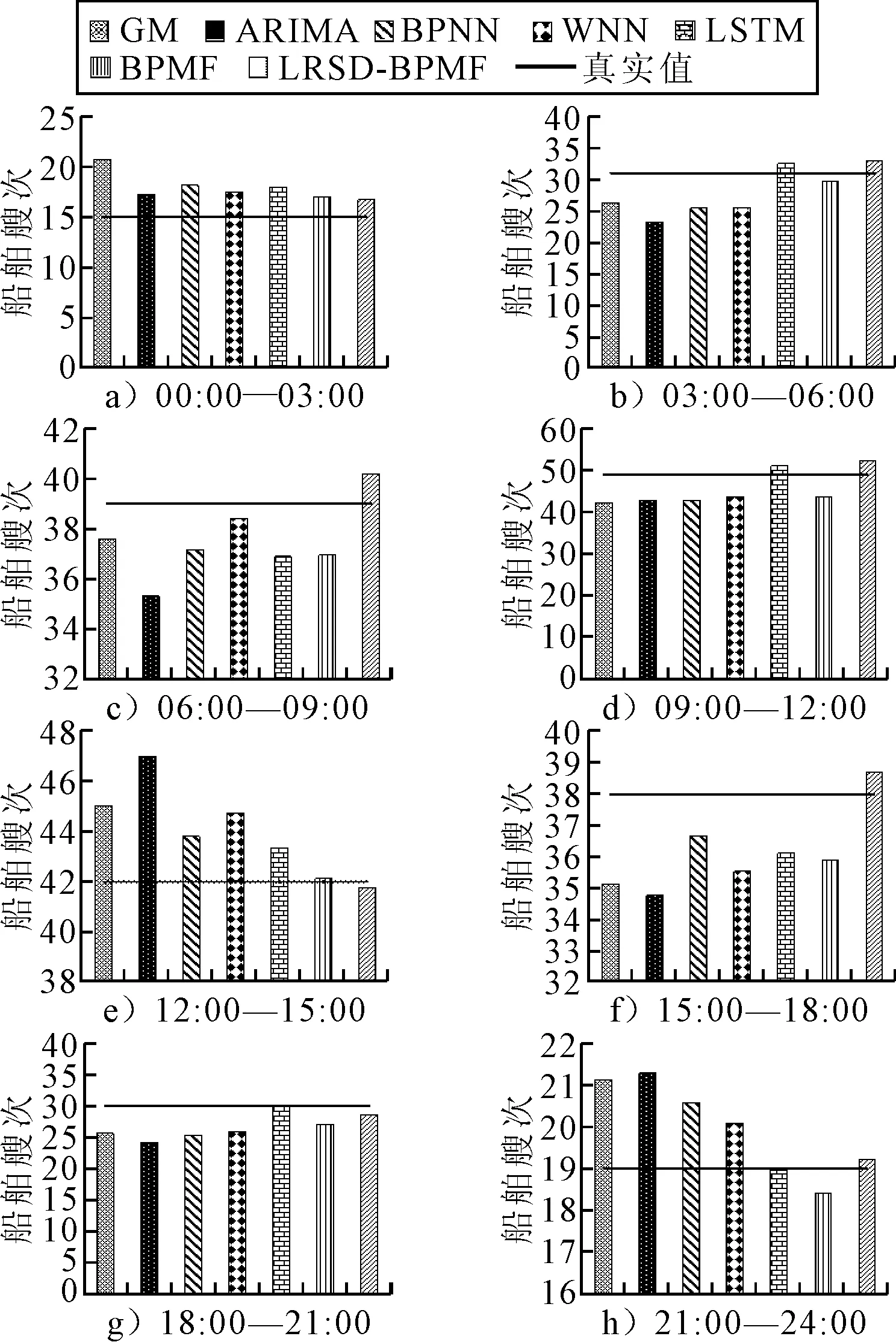
图2 各预测模型计算结果对比图
2.3 预测结果精度评价
选择均方误差(mean-square error,MSE),均方根误差(root mean square error, RMSE),相对误差(relative error, RE)及标准差(standard deviation, STD)对各模型的预测结果进行综合评价.各评价公式为
(16)
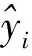
均方误差可以评价数据的变化程度,MSE值越小,则说明预测模型预测的实验数据越精确.
(17)
均方根误差是均方误差的算术平方根,当对某一时段的数据进行多次预测时,可以通过均方根误差来表示预测精度,预测精度越高,均方根误差越小.
(18)
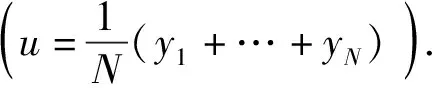
(19)
2.4 实验结果分析
由图2可知,LRSD-BPMF预测模型的预测结果与真实值从趋势到每一时间段的数值大小上相似度最大,其次是BPMF的预测结果波动较小,与LSTM在走势上的相似度较大;然后是WNN和BPNN预测模型的预测效果相对来讲要劣于BPMF;GM及ARIMA的预测结果大部分与实际值的差值较大,预测结果相对较差.
通过对实验结果进行分析,各模型对各时段预测结果的MSE、RMSE值见图3.
MSE与RMSE越小则模型预测精度越高,通过对8个时间段的预测结果进行比较,GM、ARIMA 由图3c)可知,LRSD-BPMF预测模型的相对误差及标准差最小,其预测结果可信度最高.故LRSD-BPMF模型相较于其他预测模型,具有更通过对实验结果及实验模型进行分析,参数法GM、ARIMA由于其对波动性数据无法处理,所以相较于非参数法BPNN、WNN、LSTM模型充分考虑数据波动性和平稳性,所以对于船舶交通流的预测有了较好的效果.但是参数法非参数法考虑的都只是船舶交通流的时间属性,没有考虑船舶交通流的空间属性的影响.本文提出的模型,是在考虑了船舶交通流平稳性和波动性的基础上,对交通流时空属性也充分考虑,所以预测效果较好. 图3 各模型预测结果 文中提出一种基于低秩稀疏矩阵分解和贝叶斯概率矩阵分解的船舶交通流预测模型.通过对比其他现在应用较多的神经网络及机器学习算法预测模型来讲,矩阵分解比较容易通过编程来实现,同时其时间及空间的复杂度较低,预测精度较高,并且具有很好的拓展性.但该预测模型的算法,在算法的计算速度上耗费时间较长.同时在算法训练上仍依靠大量的历史数据进行训练,所以在算法优化方面仍有一定的提升空间,后续将通过对各种算法进行进一步优化,以提升模型的预测精度及预测效率.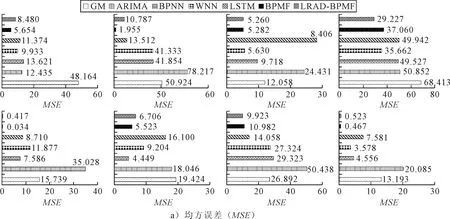
3 结 束 语

