基于SAP2000的傅式谱对结构地震响应的影响研究
曹宇轩 王志涛
(北京工业大学抗震减灾研究所 北京 100124)
0 引 言
由于地震动的随机性及复杂性,时程分析结果受地震动的影响很大,如何选择可靠的地震动输入一直是个很大的难题.地震动的研究从最初的假设为平稳随机过程[1]到强度非平稳随机过程[2],再到目前的强度-频率非平稳随机过程,以求尽可能全面描述地震动的工程特性[3].目前被人们普遍接受的地震动三要素为:幅值、持时,以及频谱特性,其中频谱特性中的傅式幅值谱及傅式相位谱对地震动的非平稳特性有着很大的影响,幅值谱反应了地震动能量在频域方面的变化规律,相位谱则与地震动时程变化规律有着紧密的联系.
在过去的几十年当中,许多学者对于傅式幅值谱和傅式相位谱展开了研究.Brune[4]提出了关于震源处加速度幅值谱模型,把该模型表示成为了关于震源处剪切波速、岩石密度、震中距等因素的相关函数;Boore[5]考虑地震动的衰减效应和场地效应,把傅式幅值谱表示为震源傅式幅值谱、衰减效应函数和场地效应函数的乘积;赵凤新等[6]通过理论公式推导得到了地震动强度同幅值谱及相位差谱的关系,从理论上论证了当相位差谱的统计依赖频率时,幅值谱与相位谱同样对时程强度有影响;朱昱等[7]利用对数正态分布概率密度函数拟合了138条实际地震动相位差谱频数分布,通过均值和标准差产生符合概率分布的相位差谱,以此为基础提出了一种人工合成地震动的方法;金星等[8]提出了用等效群速度表示相位谱的表达式,从理论上阐述了地震动相位信息是构成地震动强度和频率非平稳的主要因素.可以看出,现有的关于相位谱和幅值谱的大多数研究是从地震动自身的特性出发,而关于其本身对于结构的影响方面的研究涉及较少.
文中综合考虑了场地条件、震级的影响因素后对地震动进行分组,通过傅里叶变换分析地震动频域特征,以差异化的幅值谱和相位谱为基础构造多组不同类别的人工地震动时程曲线,分别针对典型的抗震、隔震结构开展时程分析,揭示其对不同结构地震反应的影响规律.
1 地震动集构造与结构分析模型
1.1 地震动记录选取与处理
地震动记录数据来自目前使用较为广泛的美国环太平洋地震研究中心(PEER),考虑到中美关于场地类型的划分标准不同,以文献[9]提供的转化关系为依据,按照表1的对应关系对地震动所处的场地类型进行了转化.

表1 VS30数值与中国场地类别对应关系
已经有研究表明[10-11]:场地条件和震级对于地震动的影响不容忽视.因此,在分析相位谱和幅值谱对结构地震响应影响的同时也不能忽视场地和震级所带来的影响.根据收集到的地震动记录来看,IV类场地的地震动数量有限,考虑到小样本数据下时程分析结果精度不能保障,故本文暂未考虑IV类场地情况.在将地震动按照I、II、III类场地分组后,进一步将地震动记录按震级5~6级的中强震、6~7级的强震、大于7级的大地震划分为三组,从每个分组中随机挑选出10条天然地震动,构成本文研究的地震动集.
1.2 地震动集构造
考虑到地震动记录初始时刻和末端时刻边界的影响因素,根据文献[12]采用相对峰值持时的定义,即首末两次达到或者超过峰值加速度20%的时段作为研究对象对地震动数据进行截取,使其具有相同的记录持时,然后通过比例法对地震动记录进行整体调幅处理,为
(1)


这样便得到了用于弹性分析的九组地震动集和用于弹塑性分析的九组初始地震动集(每组中各有10条地震动记录).对其中的每条地震动记录a′(t)进行傅里叶变换,得到傅里叶谱为
(2)
式中:N为地震动时程记录采样点数;t为地震动记录持时;ωn的计算公式为
ωn=nΔω
(3)
(4)
式中:Δω为傅里叶谱的圆频率步长;Δt为地震动记录时间间隔.
傅里叶幅值谱为
A(ω)=|F(ωn)|
(5)
傅里叶相位谱为
(6)
式中:Re和Im分别为F(ωn)的实部和虚部.
通过傅里叶逆变换,生成新的人工地震动,为
(7)
以I类场地震级在5~6级并经过预处理后的地震动分组为例进行说明:组内10条天然地震动分别进行傅里叶变换生成相应的幅值谱和相位谱,选取1号地震动的相位谱,分别叠加其余各地震动的幅值谱,进行傅里叶逆变换,生成10条具有相同相位谱不同幅值谱的人工地震动;同理选取1号地震动的幅值谱,分别叠加其余各地震动的相位谱,得到10条具有相同幅值谱不同相位谱的人工地震动.通过两条天然地震动记录A和B为例进行图示说明,根据前文所述式(2)~(6)获得A、B地震动幅值谱和相位谱(见图1~2),之后,根据式(7),获得具有相同相位谱、不同幅值谱和具有相同幅值谱、不同相位谱人工地震动时程曲线见图3~4.
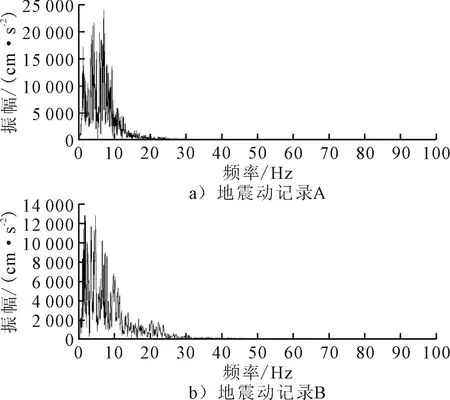
图1 地震动幅值谱
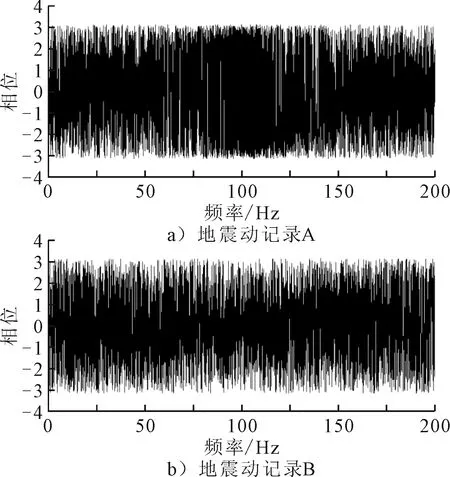
图2 地震动相位谱
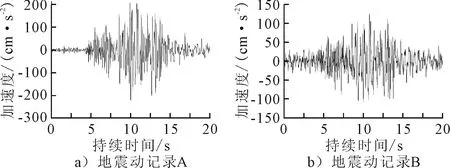
图3 相同相位谱、不同幅值谱地震动加速度时程曲线图
在记录前期地震动曲线上升阶段以及记录后期的衰减阶段加速度数值差异比较明显,在记录中期地震动的峰值加速度以及到达峰值的时间均有所不同,可见无论是幅值谱还是相位谱均对地震动时程曲线起到控制作用.
依据峰值加速度、场地和震级的不同,具有相同相位谱不同幅值谱和具有相同幅值谱不同相位谱的地震动各分为18组,其中峰值加速度为35 cm/s2和220 cm/s2各9组,每组10条人工地震动,构成了用于结构时程分析的地震动输入,见表2.
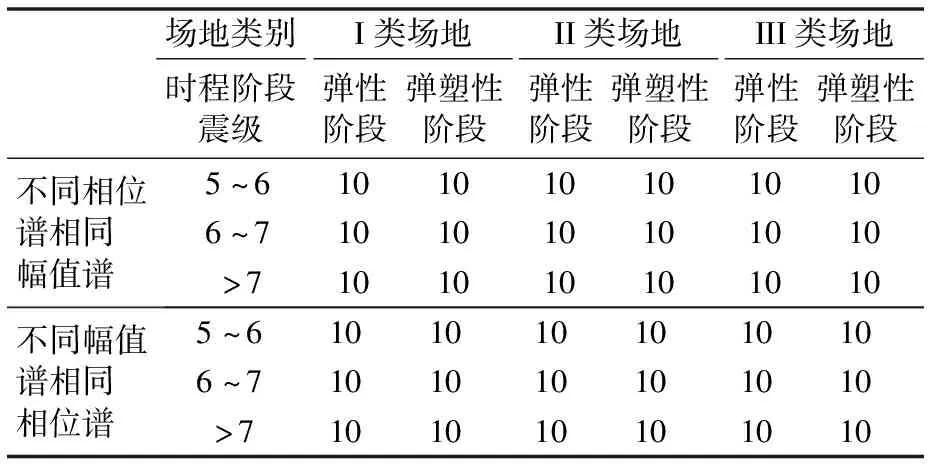
表2 地震动集分组情况 单位:条
1.2 有限元模型构建
1.2.1工程概况
结构模型采用典型钢筋混凝土框架结构,层数为6层,底层层高3.6 m,标准层层高3 m,建筑总高度18.6 m.拟建场地抗震设防烈度为7度,设计基本地震加速度峰值为0.1 g,设计地震分组为第2组.梁、柱纵筋为HRB335,箍筋为HPB300;梁、柱混凝土等级均为C40;纵向4跨,横向3跨,柱距均为6 m;梁截面尺寸均为300 mm×600 mm,1~3层柱截面尺寸500 mm×500 mm,4~6层边柱尺寸500 mm×500 mm,中柱尺寸400 mm×400 mm.
1.2.2有限元模型的建立
根据建筑设计,利用PKPM软件建立结构分析模型,对模型进行初步分析,确定结构满足基本设计要求,然后把模型导入SAP2000中,进行结构动力时程分析.
由于结构配筋等设计采用PKPM软件,时程分析采用SAP2000有限元软件分析,为保证结构分析的可靠性,因此有必要对PKPM和SAP2000建立的同一结构模型进行对比分析,确保建立的模型一致,见图5.
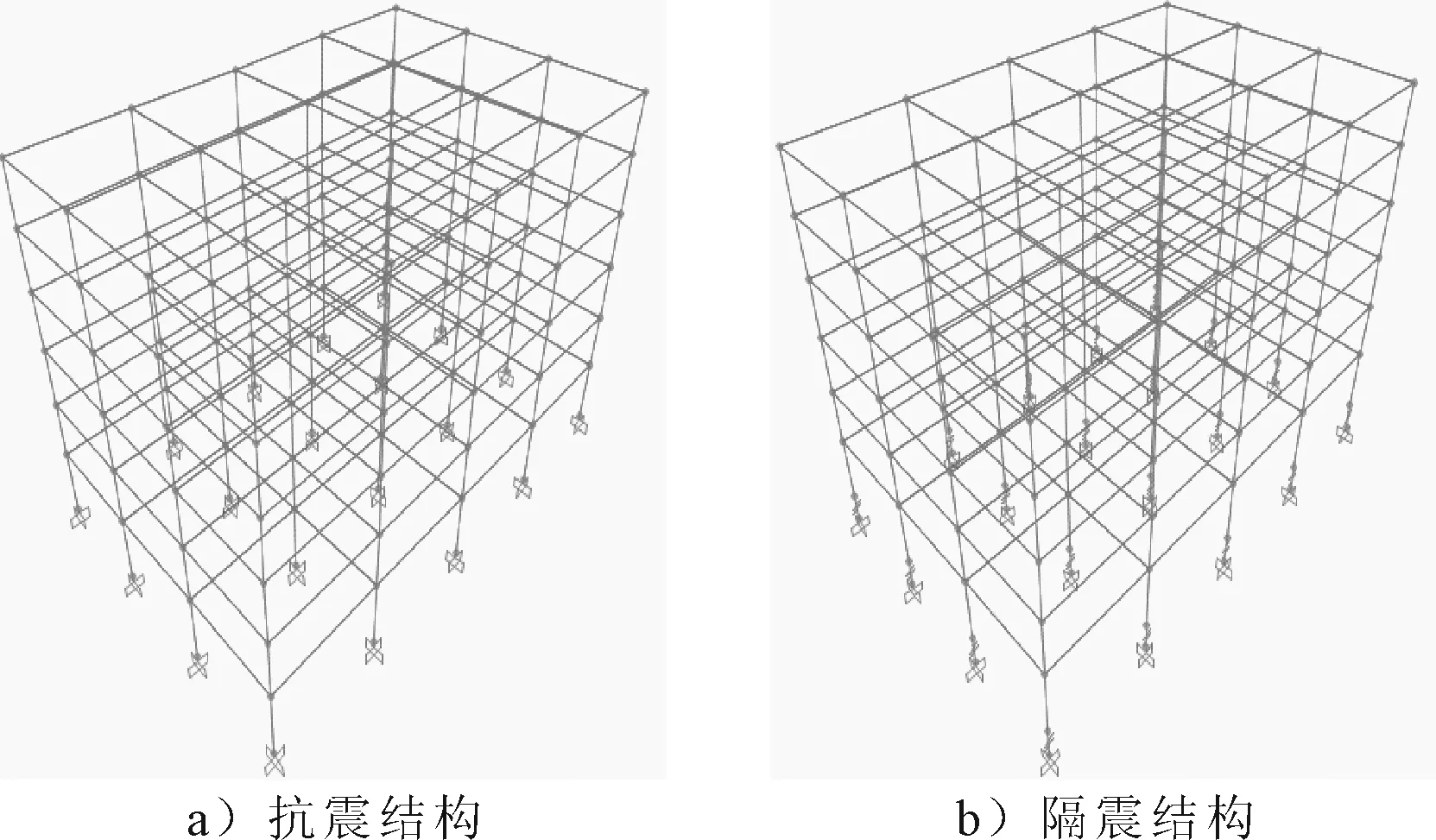
图5 SAP2000结构模型
通常来说,结构模型计算得到的周期和质量差异不大,则可以认为构建的模型相同.本文所构建的结构质量、前三阶振型周期对比分析见表3~4.

表3 抗震结构质量对比
由表3可知:PKPM软件与SAP2000软件中结构质量差值为1.98%;由表4可知:结构前三阶振型周期最大差值仅为0.86%,质量与周期的差值均很小.综合来看,PKPM与SAP2000构造模型基本一致,可以利用SAP2000构建的抗震、隔震模型进行结构时程分析,其中隔震结构采用普通橡胶隔震支座LRB500,柱底隔震,隔震层高为1.2 m.抗震、隔震结构在进行弹塑性时程分析时,距离梁、柱端部5%处形成塑性铰.
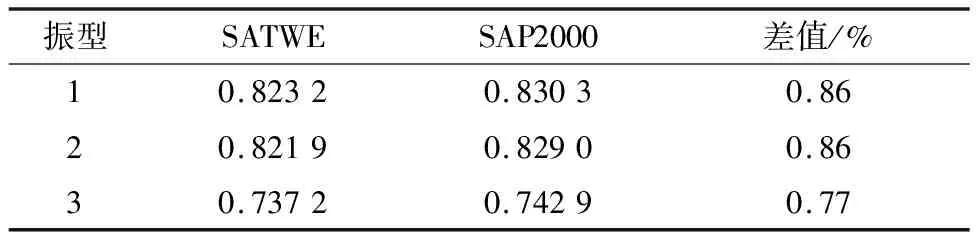
表4 抗震结构周期对比
1.3 结构地震响应评价指标
为了评估地震动傅氏谱对结构地震响应的影响,以结构最大层间位移作为结构地震响应的评价指标,以极差比(U)表征差异性,以标准差(S)作为结构地震响应离散程度的评价指标来表征差异化傅氏谱的影响,数值越大说明离散程度越大,地震动相位谱和幅值谱对于结构地震响应的影响程度也就越大.极差比和标准差计算公式为
(8)
(9)
2 傅式相位谱和幅值谱对结构地震反应影响分析
2.1 相位谱对结构地震反应影响分析
1)弹性反应 将峰值加速度为35 cm/s2的9组具有相同幅值谱和不同相位谱的人工地震动分别作用在抗震和隔震结构上,通过SAP2000软件进行弹性时程分析,因篇幅原因没有给出结构各层最大层间位移图示.由于结构最大层间位移发生在首层,给出首层层间位移对比表,见表5.
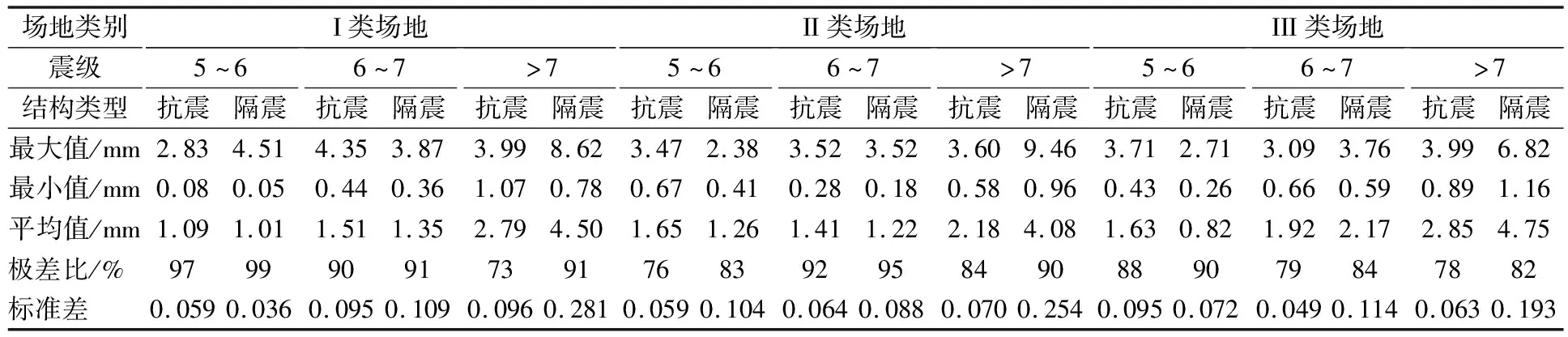
表5 首层层间位移对比表
从首层层间位移对比表可以看出,在不同相位谱作用下结构最大层间位移的极差比均在70%以上,最大甚至能够达到99%,可见差异化的相位谱对于抗震和隔震结构在弹性阶段的地震响应具有非常大的影响.从标准差数值分析结构离散性来看,同组地震动在不同的场地、震级情况下离散程度有所区别.横向来看,相同的地震动作用抗震、隔震结构上,通常是隔震结构离散性要大于抗震结构的离散性,只是在III类场地震级在5~6级情况下抗震结构的离散性比隔震结构大;纵向来看,随着震级的增加,离散性呈现增大的趋势,但是III类场地抗震结构和II类场地的隔震结构没有呈现出这样的规律性.
2)弹塑性反应 将峰值加速度为220 cm/s2的9组具有相同幅值谱和不同相位谱的人工地震动分别作用在抗震和隔震结构上,通过SAP2000软件进行弹塑性时程分析,给出不同场地条件,震级5~6情况下的各层最大层间位移对比图见图6~8.其中加粗曲线为平均值,隔震结构0层代表隔震层最大层间位移情况.首层层间位移对比表见表6.
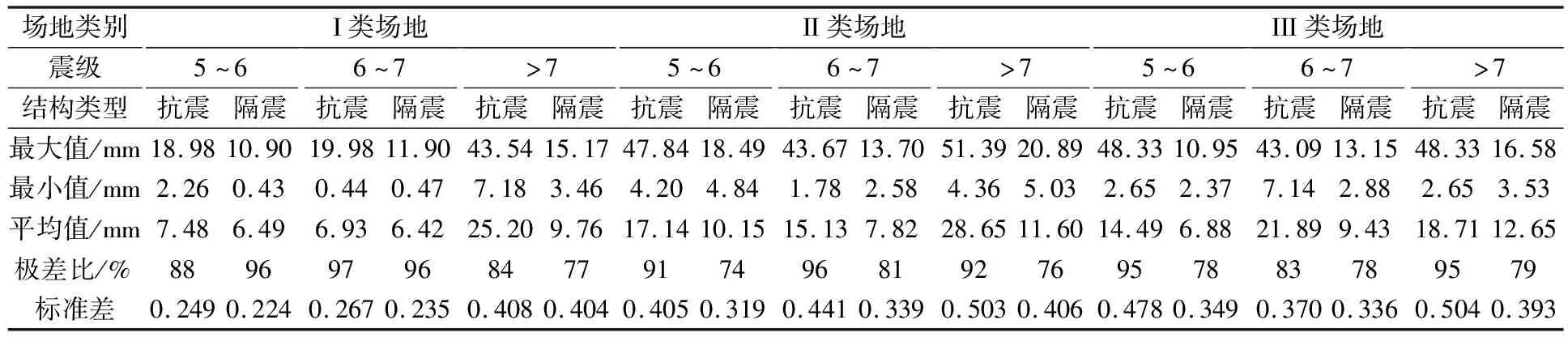
表6 首层层间位移对比表
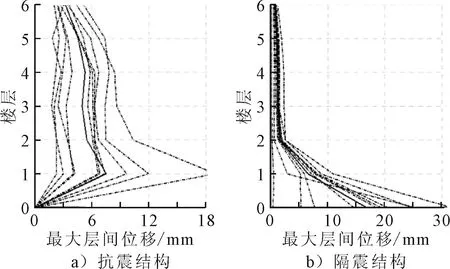
图6 I类场地5~6级震级结构地震响应
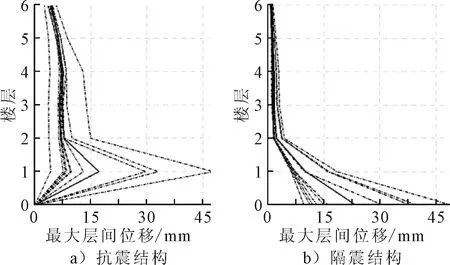
图7 II类场地5~6级震级结构地震响应
从图像和首层层间位移对比表数据分析来看,具有不同相位谱、相同幅值谱的人工地震动作用在结构上的差异性非常大,同弹性时程分析一样结构的极差比均在70%以上.通过标准差数值分析,总体来说结构弹塑性反应阶段离散程度明显大于弹性反应阶段,不同的场地、震级离散程度有所差异.横向来看,相同的地震动作用抗震、隔震结构上,抗震结构离散性要大于隔震结构;纵向来看,随着震级的增加,抗震和隔震结构的离散性呈现出增大的趋势,只有在III类场地震级为6~7级情况下没有体现出来.同时随着场地条件由I类到III类,在相同震级下,抗震结构和隔震结构离散性呈现出增大的趋势,但在III类场地震级为大于7级情况下隔震结构没有体现出这一特点.

图8 III类场地5~6级震级结构地震响应
无论是抗震结构还是隔震结构,其地震响应在弹性以及弹塑性阶段均受到相位谱的影响,其中,不同的场地与震级条件下其离散程度也是有所区别.
2.2 幅值谱对结构地震反应影响分析
1)弹性反应 将峰值加速度为35 cm/s2的9组具有相同相位谱和不同幅值谱的人工地震动分别作用在抗震和隔震结构上,通过SAP2000软件进行弹性时程分析,因篇幅原因没有给出结构各层最大层间位移图示.结构首层层间位移情况见表7.
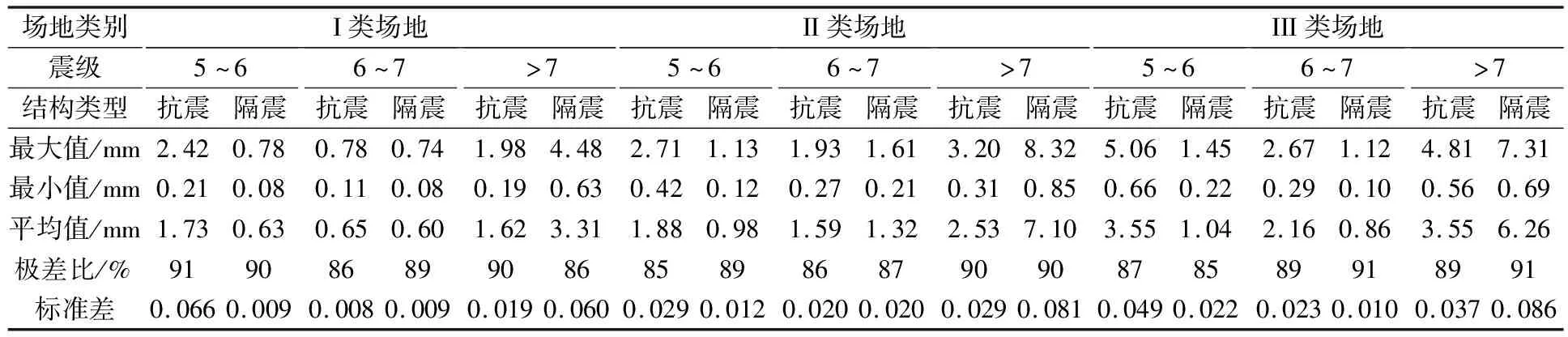
表7 首层层间位移对比表
由表7可知,结构的极差比均在80%以上,说明幅值谱同样对抗震和隔震结构的地震响应具有非常大的影响.通过标准差数值横向对比来看,在同一组地震动分别作用于抗震、隔震结构上,表现出抗震结构的离散性要大于隔震结构,但在震级大于7级的地震动作用下隔震结构的离散性要大于抗震结构;纵向对比来看,随着震级的增加,在震级大于7级的地震动作用下隔震结构离散性明显增大.同时,随着场地类别由I类到III类,抗震与隔震结构的离散性在大部分情况下都呈现出增大的趋势,抗震结构在震级为5~6级时和隔震结构在震级为6~7时则没有体现出这一规律性.
2)弹塑性反应 将峰值加速度为220 cm/s2的9组具有相同相位谱和不同幅值谱的人工地震动分别作用在抗震和隔震结构上,通过SAP2000软件进行弹塑性时程分析,给出III类场地、不同震级情况下的各层最大层间位移图见图9~11.其中加粗曲线为平均值,隔震结构0层代表隔震层最大层间位移.首层层间位移情况见表8.
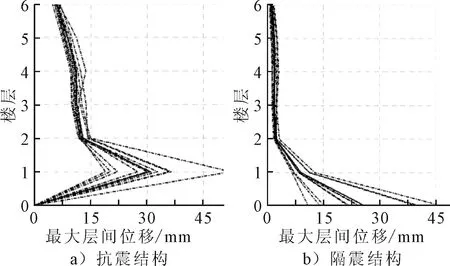
图9 III类场地5~6级震级结构地震响应
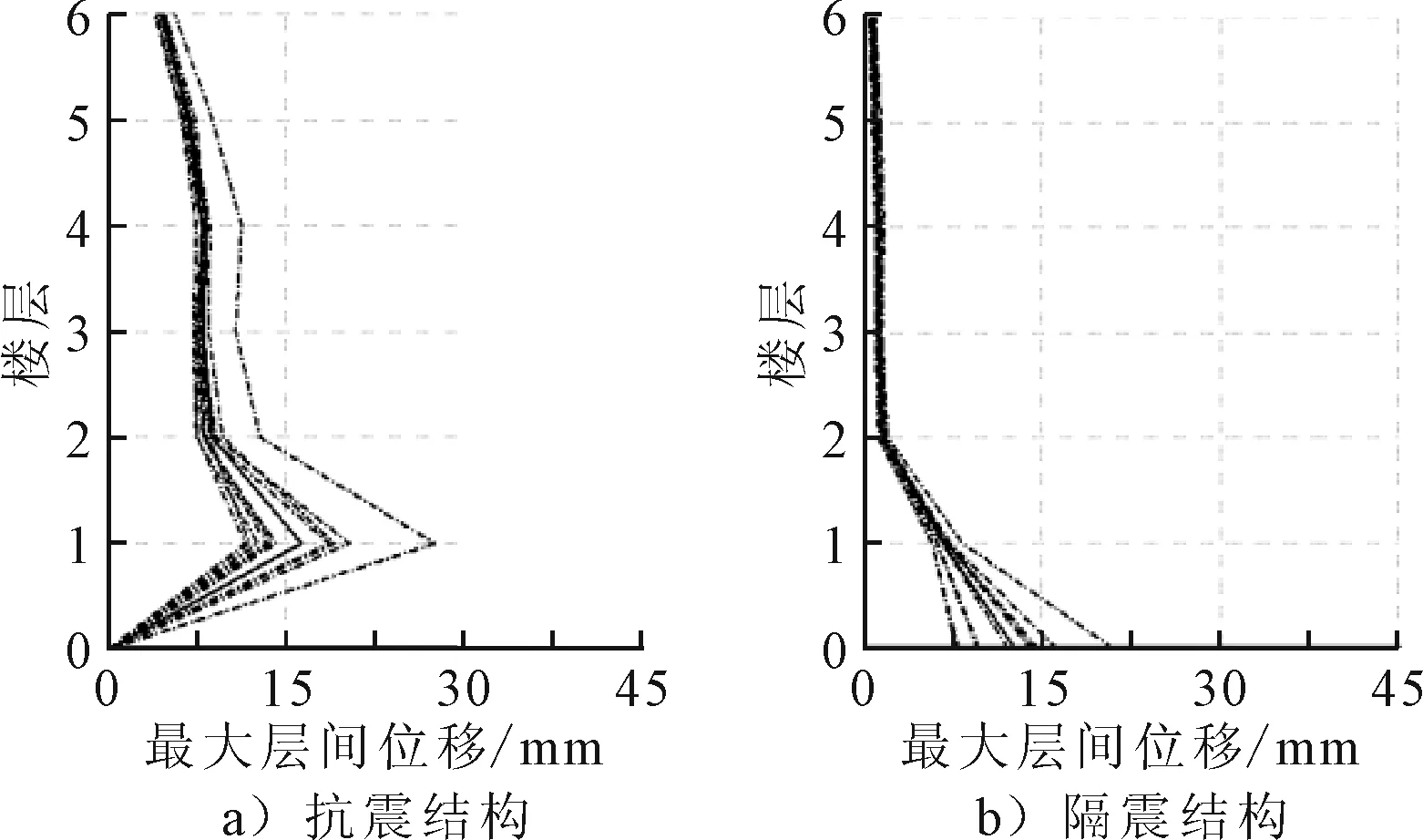
图10 III类场地6~7级震级结构地震响应
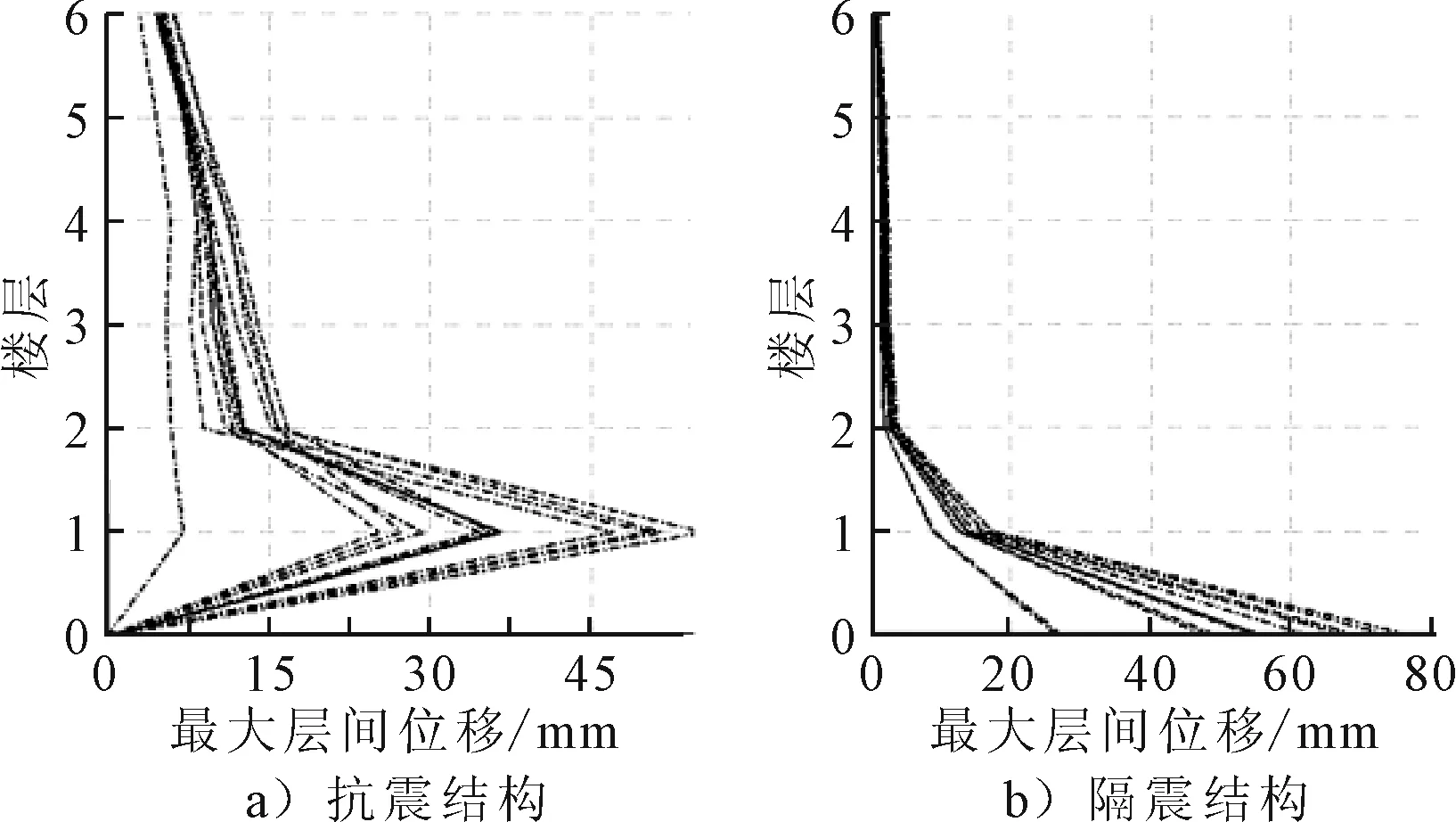
图11 III类场地大于7级震级结构地震响应
从图像和首层层间位移对比表来看,结构极差比数值绝大部分在80%以上,同弹性时程分析一样,幅值谱对于结构在弹塑性阶段的地震响应具有非常大的影响.
通过标准差数值分析看出不同的场地、震级离散程度有所区别.总体来说结构弹塑性反应阶段离散程度要明显大于弹性反应阶段,横向对比来看,相同的地震动作用抗震、隔震结构上,通常是抗震结构离散性要大于隔震结构,在震级大于7级的情况下,隔震结构的离散性有了明显的增加,出现了隔震结构离散性大于抗震结构的情况;纵向来看,随着震级的增加,抗震和隔震结构离散性呈现出增大的趋势,但在III类场震级为6~7级情况下隔震结构没有体现出这一特点.随着场地条件由I类到III类,抗震和隔震结构的离散性呈现出增大的趋势,只有在震级为6~7级的情况下隔震结构没有体现出这一特点.
综合分析极差比以及标准差,可以看出无论是抗震结构还是隔震结构,其地震响应在弹性和弹塑性阶段均受到幅值谱的影响,其中根据场地条件以及震级的不同,结构离散程度也是有所差异.
3 结 论
1)地震动相位谱和幅值谱对于结构的弹性反应、弹塑性反应均有一定的影响,对于地震反应的影响不能忽略,在今后的时程分析相关研究中,除了传统考虑的峰值、持时以及反应谱等因素外,相位谱和幅值谱的影响情况也应该给予充分考虑.
2)虽然事先对于地震动进行了预处理,使每条地震动的相对持时及峰值加速度基本一致,但是通过标准差分析来看,无论是具有不同相位谱还是不同幅值谱的地震动作用在结构上,结构弹塑性阶段时程反应离散性均大于弹性反应阶段的.
3)结合场地条件及震级情况,在大部分情况下随着震级的增大、场地条件由I类到III类,结构的最大层间位移和离散性呈现出增大的趋势.通常而言,抗震结构在相同情况下的离散性要大于隔震结构的离散性,然而其中仍有个别情况增加趋势不是很明显或者存在不相符之处.
虽然根据场地条件以及震级两个因素对天然地震动做了比较详细的划分,获得了比较全面的地震动集,并且在每个子集中随机挑选地震动,致使分析结果能够体现出一些变化规律以及变化趋势,但是每个子集中的样本数量稍显不足.若想获得更为精确的一般规律,仍需进行进一步的验证工作.

