基于信号分解和深度学习的农产品价格预测

王润周，张新生，王明虎

基于信号分解和深度学习的农产品价格预测

王润周，张新生※，王明虎

（西安建筑科技大学管理学院，西安 710055）

农产品价格的稳定对社会经济与农业发展有重要意义，但农产品价格的波动具有非平稳、非线性、波动性大的特性，较难精确预测。该研究基于信号分解和深度学习，提出一种分解-重构-提取-关联-输出的农产品价格预测模型（CT-BiSeq2seq），并且加入平均气温、养殖成本（大猪配合饲料与尿素价格）、群众关注度等多维度数据来提高模型的预测精度。首先，采用互补集合经验模态分解（Complementary Ensemble Empirical Mode Decomposition，CEEMD）方法把复杂的原始价格序列分解为简单序列。其次，分析皮尔逊相关系数及分解后的子序列，把原始价格序列重构为高频项、低频项、残差项。再经过时间卷积网络（Temporal Convolutional Network，TCN）提取重构序列的数据特征。随后，构建Biseq2seq模型，解码器引入双向长短期记忆网络（Bi-directional Long Short-Term Memory，Bi-LSTM）加强序列数据间的全局关联。最后，通过解码器的LSTM网络输出预测值。以北京丰台区批发市场的白条猪肉价格进行实证分析，该研究提出的CT-BiSeq2seq模型的预测性能显著优于其他价格预测基准模型，在滞后天数为11 d达到最优效果。在其他数据集也有精确和稳定的预测效果，菠菜、苹果，鸡蛋的均方误差分别为0.627 7、0.463 2、0.552 6元2/kg2，平均绝对误差分别为0.543 1、0.442 5、0.533 9元/kg，平均绝对百分比误差分别为3.204 7%、2.236 1%、2.231 4%。同时根据不同数据集的结果发现，价格波动大的农产品适合采用较大的滞后天数，价格波动小的农产品适合采用较小的滞后天数。该模型可以为预测农产品的价格波动提供参考。

农产品；价格预测；互补集合经验模态分解；时间卷积网络；双向序列到序列模型；长短期记忆网络

0 引 言

中国是农业大国，农产品价格的波动影响着民生以及国民经济的稳定发展。随着2019年非洲瘟疫蔓延、国家新环保养殖政策的颁布及2020年新冠疫情的爆发，农产品的非正常价格波动逐渐增多，如截止到2019年9月初大蒜价格已回涨至9.19元/kg，较2004年大蒜批发价格的平均值高出56.29%，出现了“菜比肉贵”的热议；2020年初猪肉价格相比2019年中旬的价格增长54.11%[1]。非正常的农产品价格波动严重影响着人民的生活安定和国家经济的稳定发展，因此建立精准的农产品价格预测模型，预防突发事件对人民生活的影响，对解决“三农”问题及农业信息化建设具有重要作用。

目前，对农产品价格的预测研究主要分为传统计量统计方法、人工智能方法及组合模型三类预测方法，且各类方法按时间顺序不断发展。传统计量模型方法有较扎实的理论基础，对于不同问题有较强的可解释性，如回归分析、向量自回归（Vector Autoregressive，VAR）、自回归滑动平均（Autoregressive Moving Average，ARMA）、整合移动平均自回归（Autoregressive Integrated Moving Average，ARIMA）、广义自回归条件异方差（Generalized Autoregressive Conditional Heteroscedasticity，GARCH）等模型早期被广泛应用于价格预测[2-3]，可以准确预测绿豆价格[4]、大豆期货价格[5]等短时序的农产品价格。随后，一些传统计量方法结合不同农产品价格的特点进行改进，使得模型的预测能力随着历史数据的丰富逐渐与真实数据趋近[6-7]。以上研究丰富了传统的价格预测研究，使传统计量统计方法逐渐形成了系统的时间序列预测模型。然而传统计量统计方法较难完整表示长时间序列的非平稳、非线性及多尺度特征，在处理非线性问题上有较强的局限性[8]。

机器学习、深度学习等人工智能方法的发展弥补了传统计量统计方法的不足，可处理较长时序、非线性、非平稳的价格预测问题，常见模型有BP神经网络（Back Propagation Neural Network）、支持向量机（Support Vector Machine，SVM）、动态神经网络（Dynamic neural network）、时间卷积网络（Temporal Convolutional Network，TCN）等[9-12]。相比于传统计量统计方法，这些模型具有较高的准确率、鲁棒性和泛化性，可以更加精准地预测农产品价格。但很难有一种人工智能方法可以解决所有不同预测情境下的问题[13]。一方面，在处理高维度、大数据量的预测问题时，SVM、BP神经网络等浅层次机器学习算法存在较大局限性，会出现参数的维数灾难与无效的特征表示等问题[14]。另一方面，虽然单一模型预测误差波动较大，总体上随着预测周期变长精度下降。但在实际预测上，并非所有的人工智能模型都优于传统统计计量预测方法[15-16]。因此，应根据数据与任务的特点，选择适合的预测模型。

组合模型通过结合传统计量统计方法、智能优化算法、人工智能方法的优点，对预测问题设置先验假设和数据处理，减少学习偏差，较大程度增强预测模型的拟合能力[17]。在研究方法上，学者们逐渐形成了分解-重构-输出的集成模式[18-23]。首先采用小波分解、集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD），奇异谱分析（Singular Spectrum Analysis，SSA）等方法，将原始数据序列分解、简化，剔除时间序列中的噪声。随后通过智能搜索算法、-means聚类方法等进行参数优化与序列重构。最后使用SVM、长短期记忆网络（Long Short-Term Memory，LSTM）等模型输出结果。在预测性能上优于大部分单模型方法，显著提升了预测模型的适用范围和预测精度[24]，因此本文采用组合模型进行农产品价格预测。

综上，组合模型在价格预测上有着独特的优势，但仍然存在不足之处：1）基于SSA、EEMD等分解方法虽然能将复杂信号序列分解成多个简单序列，更清晰地认识复杂信号里的运动规律和结构，但存在计算量过大、残余辅助噪声较大等问题；2）重构后的特征序列缺乏数据间的时间序列关系，且全局关联度不高，预测容易出现波动；3）当前农产品价格的深度学习预测模型主要采用循环神经网络（Recurrent Neural Network，RNN）、LSTM等网络，其输入步数等于输出步数，需要经过全连接层压缩才能输出预测值，不能实现任意步数的预测，且压缩过后的值相对独立，缺乏序列之间的依赖性。基于此，本文结合信号分解和深度学习，提出一种CT-BiSeq2seq农产品价格预测模型，首先采用互补集合经验模态分解方法，减少分解时所需的迭代次数，降低序列的噪声残余；其次结合皮尔逊相关系数进行序列重构；再加入多维度数据，利用时间卷积网络TCN提取农产品价格间的时间序列关系；最后构建BiSeq2seq网络，编码器引入双向LSTM网络，加强数据关联，解码器对双向LSTM的结果进行编译，实现任意步数的输出。研究结果以期为多种农产品价格的预测提供参考。

1 基于CT-BiSeq2seq模型的农产品价格预测框架

农产品长期的价格时间序列数据可能蕴含复杂的物理过程或经济规律，为更清晰地分析农产品价格的变化规律，精准地进行价格预测，本文结合信号分解和深度学习的方法，提出一种CT-BiSeq2seq价格预测模型，在提升精确性、减少数据参数的同时，实现任意步数的输出。整体框架如图1所示。

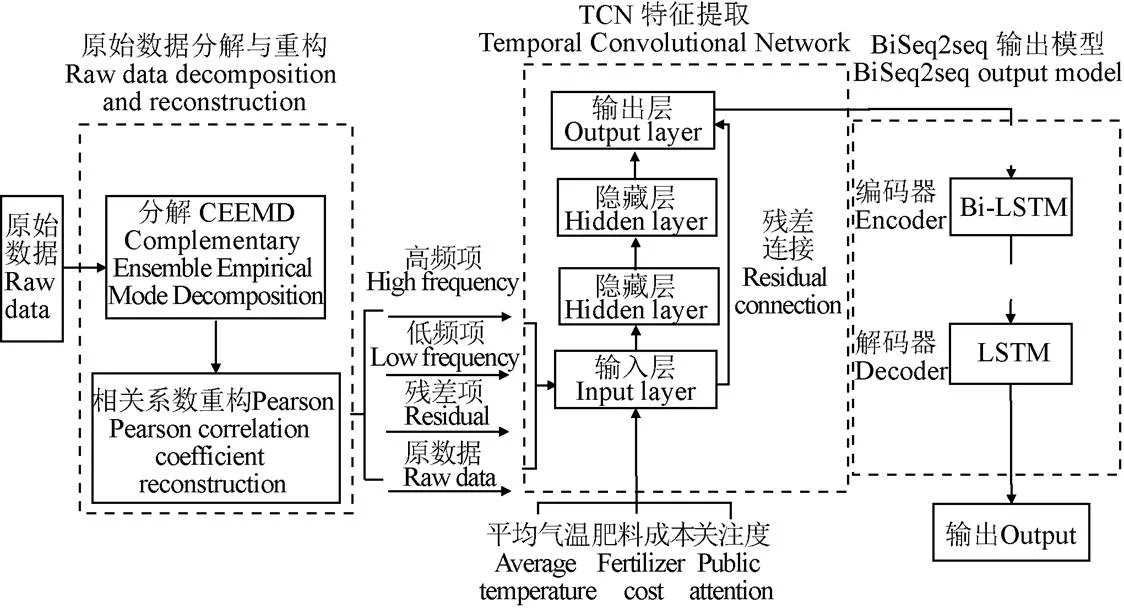
图1 CT-BiSeq2seq模型框架图

由图1可见，CT-BiSeq2seq模型主要包括5个步骤，即分解-重构-提取-关联-预测。

1）分解：首先对农产品长期的价格序列进行CEEMD分解。将复杂序列表示成多个简单信号，去除干扰信息，进行定量分析。

2）重构：其次分析皮尔逊相关系数及分解后的IMF序列，重构后得到高频项、低频项、残差项及原价格4组数据特征，分析4组数据之间的关系，并将其作为后续的输入数据。

3）提取：再者采用时间卷积网络TCN提取农产品价格的时间序列特征。

4）关联：随后提出了改进的BiSeq2seq模型，即在Seq2seq模型的编码器中引入双向LSTM网络（Bi-LSTM）正反向学习序列数据的内容，掌握全局信息的关联。

5）预测：最后在解码器部分，采用LSTM网络实现农产品价格的任意步预测。

2 理论方法

2.1 互补集合经验模态分解

互补集合经验模态分解[25]（Complementary Ensemble Empirical Mode Decomposition，CEEMD）是一种处理非线性、非平稳信号数据的方法，可将复杂信号分解为多个简单的信号。其原理是在待分解信号中加入若干组成对的、互为相反数的白噪声信号，把复杂时间序列信号分解为有限个周期不同的本征模函数（Intrinsic Mode Function，IMF）和一个残差信号，有效清除信号的噪声残余，减少分解时所需的迭代次数[26]。计算过程如下：

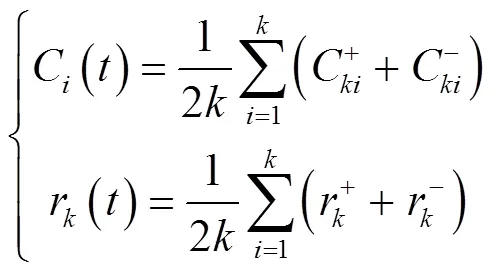
2.2 时间卷积网络

时间卷积网络（Temporal Convolutional Network，TCN）首先被提出是作为CNN网络的扩展，用于计算机视觉检测[27]。其不仅包含传统CNN的优势，如局部连接、权值共享，最重要的是包含因果卷积、扩张连接、残差连接的结构优势。利用TCN网络可以挖掘数据在时间维度上的特征并提取出更高维度的关联。

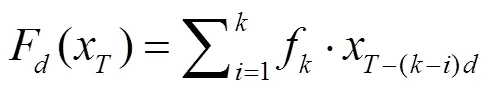
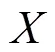
注：x为输入的时间序列数据，y为输出结果，为膨胀系数，为卷积核尺寸。

Note:xis the input time series data,yis the output result,is the dilation coefficient,is the size of convolution kernel.

图2 时间卷积网络结构图

Fig.2 Structure diagram of time convolution network

2.3 双向序列到序列模型（BiSeq2seq）

序列到序列模型（Sequence to Sequence，Seq2Seq）主要解决循环神经网络（Recurrent Neural Network，RNN）输入和输出长度不配对的问题，多用于文本翻译、语音生成领域，目前也有学者用于时间序列预测，如空气质量预测[28]。Seq2seq模型虽然在时间序列问题上有较好的预测效果，但本质上是一种单向提取序列信息的网络，整个过程容易忽略未来时刻到过去时刻方向的联系，因此在编码器引入双向长短期记忆网络，解码器引入长短期记忆网络来解决此问题，如图3所示。

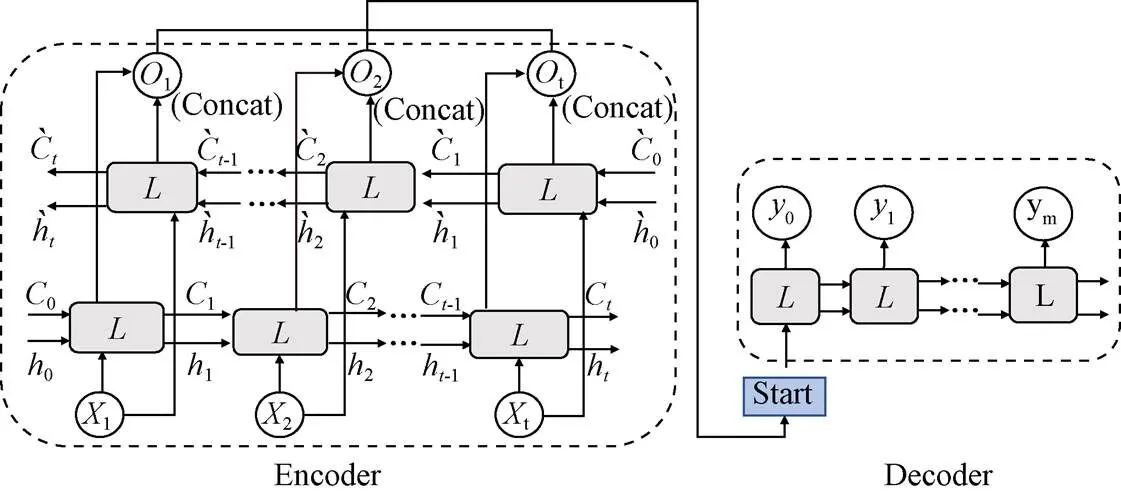
注：Xt为编码器的输入数据，Ot为编码器的输出结果，L为LSTM网络，Ct，ht分别为正向LSTM网络的记忆细胞信息与历史信息，C̀t，h̀t分别为反向LSTM网络的记忆细胞信息与历史信息，ym为解码器的输出结果。

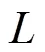
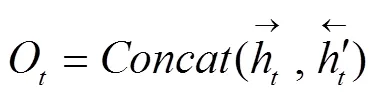
Bi-LSTM网络保留了RNN网络的重复链式结构，由两个正反方向的LSTM网络构成[29]。其中LSTM网络的结构主要由遗忘门、输入门、记忆细胞状态、输出门四部分构成，通过3种门结构来控制细胞状态传输信息。细胞状态更新的过程类似于传送带，在最上部的链条运行，整个过程有少量的线性交互。运作过程如图4所示。

注：Xt为输入结果，ht为输出结果，ht-1为历史信息，Ct为LSTM网络的记忆细胞信息，ft，it为参数矩阵，为矩阵乘法，⊕为矩阵加法。

3 实例验证

3.1 试验环境与原始数据

本文的试验基于Windows10 64位操作系统，处理器为AMD Ryzen 7 5800H with Radeon Graphics 3.20 GHz，NVIDIA GeForce GTX 3070开启GPU加速内存16 GB，编程语言采用Python3.8.12。本文基础试验数据来自全国农产品商务信息公共服务平台（新农村商网http://nc.mofcom.gov.cn/jghq/index）。本文以该网站北京丰台区农产品批发市场白条猪肉为实证对象来研究其价格走势，以该市场2016年1月1日至2022年2月28日白条猪肉的日均价格为基础进行实证分析。由于农产品价格受多种因素影响，引入多维度的影响因素有助于提高模型的预测精度。因此本文在对白条猪肉价格进行CEEMD分解与重构后，加入对农产品价格影响较大的因素：北京市每日平均气温、肥料价格（大猪配合饲料）、公众热度（百度指数）。其中气温影响农产品的生长发育；肥料价格在一定程度上影响农产品的产量；公众热度从一定程度上反映当农产品价格变化时群众的情绪，会影响消费者购买意向[30]。引入的3种影响因素数据分别来自于天气网（https://www.tianqi.com）、全国重点农产品市场信息平台（http://ncpscxx.moa.gov.cn）、百度指数（https://index.baidu.com）。本试验对数据中的缺失值、偏差较大值进行线性插值法处理，具体根据其前后价格的均值处理。最终输入变量的维度为7维，每个维度各得到2 252条价格数据，其价格走势如图5a所示，平均气温如图5b所示，肥料价格如图5c所示，公众关注度如图 5d所示。

由图5a分析可得，2016年1月至2022年2月期间白条猪肉价格波动趋势很大。整个过程呈现出非线性、非平稳的特点且无明显的价格变化规律。另外，价格走势图中前半部分与后半部分的数据分布差异较大，故难以用常规的线性模型拟合。由图5b分析可得，气温趋势呈季节性变化，通常在年气温较低时，对应价格较高。由图5c分析可得，肥料的价格呈不断上涨趋势，当猪肉价格处于2019年初至2021年出的高价阶段，肥料价格也相对较高。由图5d分析可得，群众对猪肉价格关注度比较平稳，但因为重大事件的发生会出现较大的峰值，在一定程度影响猪肉价格，例如2019年后半年“非洲猪瘟”发生，群众对猪肉价格的关注度大幅度增加，一定程度上推进了不理智购买行为，间接导致猪肉价格飙升。

图5 猪肉价格、气温、肥料价格、关注度趋势图

3.2 农产品价格序列CEEMD分解及重构

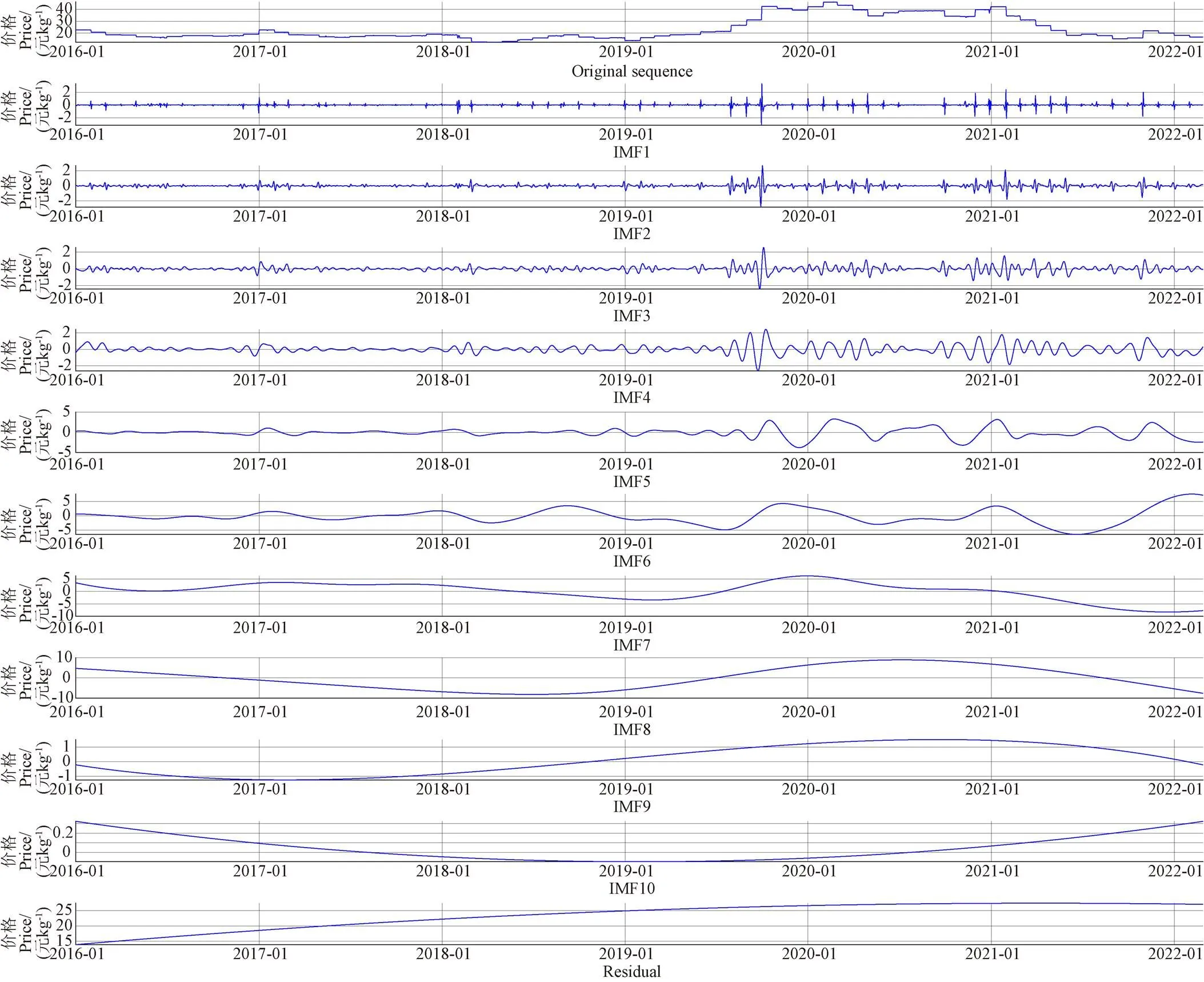
首先将白条猪肉的每日价格进行CEEMD分解，得到数据的多尺度特征。设置白噪声幅值为0.2（0-1之间，在0.2时效果最优），信号的平均累加次数为50（本试验在取值50时，得到的IMF序列最多，小于50时分解出的子序列也有较好地效果）。将价格序列数据分解后，得到了10个IMF子序列和1个残差项，如图 6示。

由图6知，每个分解后的IMF序列的振幅、频率和周期均不相同，且每个IMF序列都有自身的波动特征。从上到下分析分解后的IMF序列可得，周期不断增大，各序列数据由基本对称变为不对称，数据的平均值不断偏离0，残差项呈现近似线性上升的趋势。在第7个IMF序列时，序列图开始变得不对称。

通过计算各IMF序列间的皮尔逊相关系数，如表1所示。当在第7个IMF序列时，皮尔逊相关系数开始变化较大，数据明显偏离0；结合上述分析，故将IMF1～IMF6定为高频项，IMF7～IMF10定为低频项。

日期Date

表1 各IMF序列的皮尔逊相关系数

对原始价格序列进行重构，将高频项IMF1～IMF6的值叠加，低频项IMF7～IMF10的值叠加，残差序列保持不变，得到重构后的价格序列图如图7所示。

由图7分析可得，残差项是影响白条猪肉价格的主要组成部分，反映其价格的内在长期走势。残差项主要由供求关系决定；高频项与原始数据走势相似并且其IMF序列的均值保持在0附近上下波动。高频项对总体走势影响小，代表常规经济政策改革、期货炒作、市场供需短暂失衡、国外相关市场变化等引起的短期波动。低频项波动幅度较大，对原始数据走势产生很大影响，代表了重大事件对白条猪肉价格的影响，经对比，其波峰、波谷与重大事件基本对应，如2019年非洲猪瘟、规范养殖政策颁布、2020年新冠疫情爆发等事件。

图7 重构后的价格序列图

3.3 基于CT-BiSeq2seq模型的农产品价格预测

3.3.1 数据集划分

数据标准化的操作要在训练集数据上进行，若包含测试集数据可能会发生数据泄露的问题，将导致预测不准。故把整个数据集划分为训练集、验证集、测试集，考虑数据间的时间序列关系，本文数据集按照时间顺序划分，设定重构后的白条猪肉价格数据的前80%为训练数据与验证集，其余20%数据为测试数据，训练集、验证集、测试集所占比例分别为6∶2∶2。

由于时间序列问题预测会存在滞后性，本试验为更好确定解码器LSTM网络的预测步数，设计不同滞后天数。依据前人的研究结果[22]，当滞后天数在9～13 d时，LSTM模型在农产品价格预测效果较好。为保证模型有更好的拟合能力，本文扩大滞后天数范围，分别设置滞后天数为3、5、7、9、11、13、15 d。为保证预测精度，后续试验选择滞后天数为11 d进行预测，并进行不同滞后天数的对比试验将在3.4.2节给出。

3.3.2 数据预处理

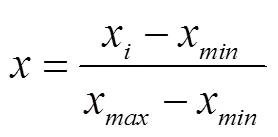
3.3.3 模型结构

CT-BiSeq2seq预测模型主要包括四个部分：第一部分为CEEMD分解、重构部分，简化序列数据信号作为输入层；第二部分，TCN模型提取时间序列的历史特征；第三部分为BiSeq2seq模型，采用Bi-LSTM网络为编码器（Encoder）加强数据间的关联，第四部分为解码器（Decoder），由LSTM网络实现多步输出。如图8所示。

试验设置8层网络结构，其中第一层为输入层，把CEEMD分解、重构后的数据转变为三维向量。第二层为TCN层，提取重构后的数据特征，输入与输出数量相等。第三层为Dropout层，本试验设置Dropout值为0.2，能够在训练过程中随机忽略20%的节点连接，防止过拟合。第四层将提取的数据特征作为输入数据。输入数据被传入到编码器中的Bi-LSTM网络，学习了预测价格与其他输入特征间的非线性关系。第五层在编码器后使用全局平均池化（Global Average Pooling），减少训练参数，增加训练速度。第六层为Repeat Vector层，将解码器的输出向量进行复制，形成具有时间步数的向量，防止时间序列数据的关系被分解。第七层为解码器中的LSTM网络，实现任意步数的输出。第八层将编码器输出的维度进行压缩，输出具体预测值。

图8 模型结构图

3.3.4 超参数设置与模型训练

采用均方误差（Mean Square Error，MSE）作为模型正向传播的损失函数，使用在优化预测误差方面性能较好的Adam算法反向传播更新权重参数与偏置[31]。同时也采用平均绝对误差（Mean Absolute Error，MAE）、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）作为衡量指标。其中MSE是预测值与真实值的绝对平方误差的平均值，一般用来检测模型的预测值和真实值之间的偏差。MAE是实际监测值与预测值之间差值的平均值，它可以反映预测值误差的实际情况。MAPE不仅考虑预测值与真实值的偏差，还考虑了偏差与真实值之间的比例，此指标对相对误差敏感，不会因目标变量的全局缩放而改变。MSE、MAE与MAPE的值越小，模型的预测精度越高[32]。各衡量指标计算公式如下。

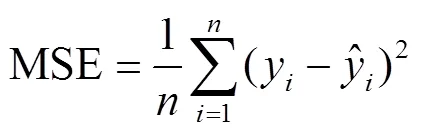
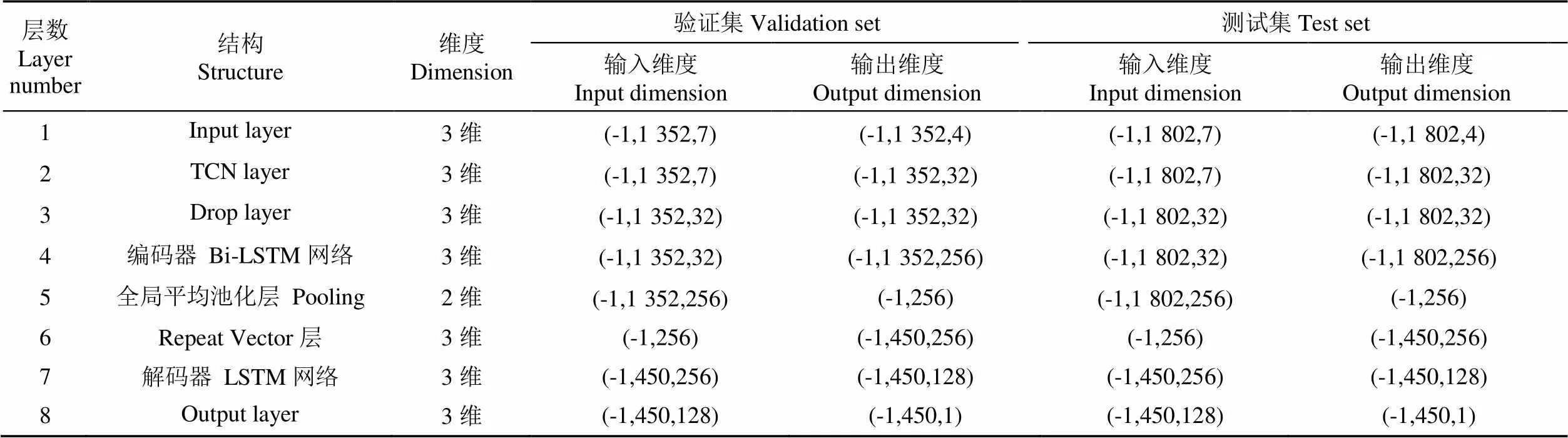
表2 模型训练的网络维度

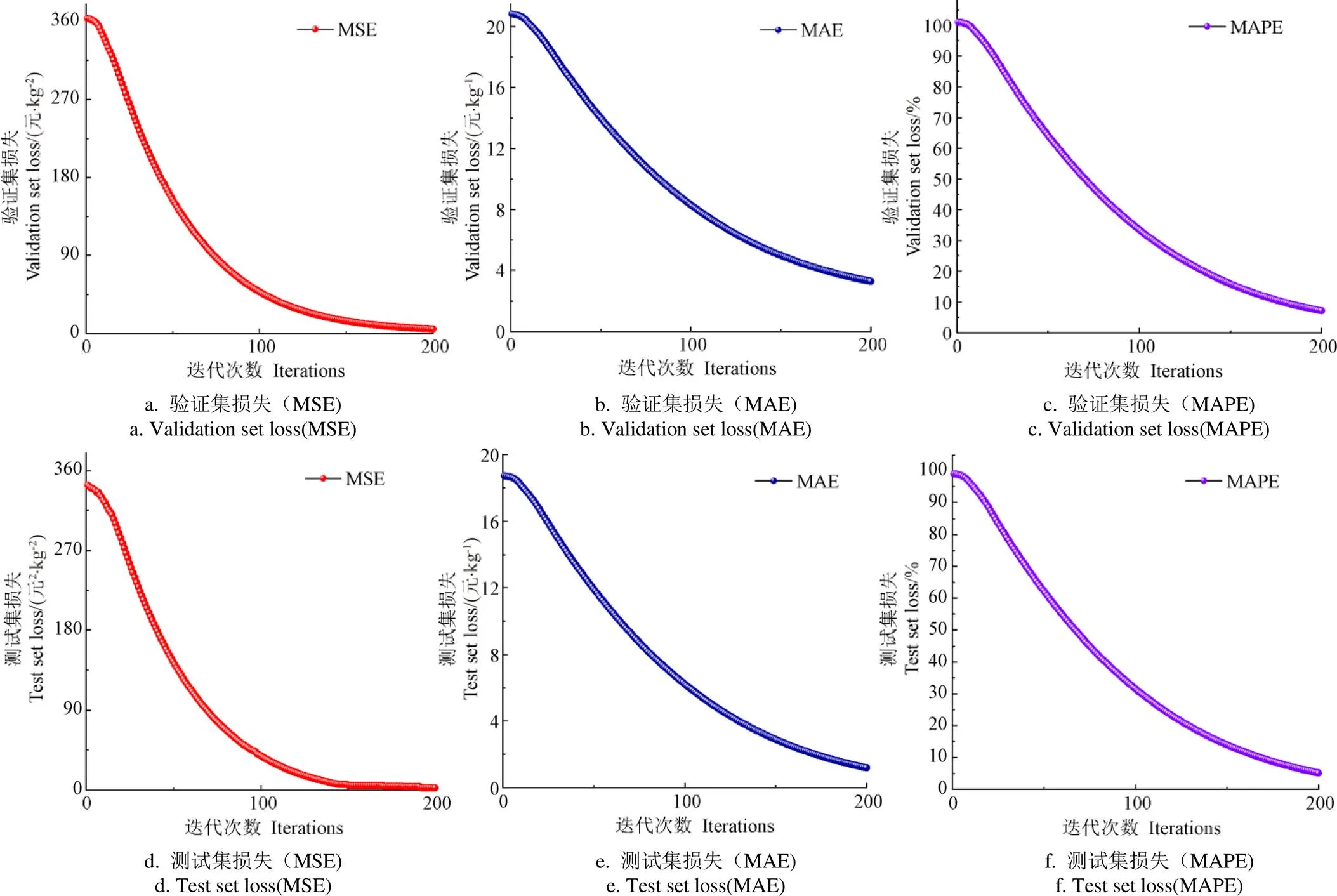
图9 验证集与测试集损失

由图9可得，验证集经过200个训练周期后，MSE、MAE、MAPE分别为0.683 7元/kg2、0.554 3元/kg、2.275 6%。测试集经过200个训练周期后，MSE、MAE、MAPE分别为0.661 1元/kg2、0.501 4元/kg、2.113 8%。验证集与训练集的误差较小，且测试集误差小于验证集误差，证明本模型在测试集有较好的拟合能力。CT-BiSeq2seq预测模型在验证集上的预测结果如图10所示，预测值与实际值拟合良好。

3.4 结果及分析

3.4.1 各模型预测对比结果

为保证测试集在不同试验中有较为一致的结果，在模型训练前加入随机数种子，种子值设为1。在测试集与其他基准模型进行对比，采用验证集的模型超参数，各评价指标、训练批次、学习率、训练周期等都保持一致。同时参考相关研究[22]，当滞后天数在9～13 d时，LSTM网络在预测农产品价格时性能较优，因此本试验采用滞后天数为11 d。为验证本模型在预测上的优势，依次与LSTM、Seq2seq、TCN-LSTM、CEEMD-TCN-LSTM、CEEMD-TCN-Seq2seq模型的预测效果进行对比，各模型预测误差结果如表3所示，预测结果如图11所示。

图10 验证集预测结果

表3 各模型的详细误差对比结果

图11 各模型对比预测结果

结合表3与图11可得，CT-BiSeq2seq模型的预测误差明显低于其他模型。具体分析，LSTM网络的预测误差相对较大，在长期预测中主要拟合出变化趋势，未能拟合出变化细节；Seq2seq模型在进行Encoder和Decoder过程后，预测损失明显减小，与LSTM的预测损失相比，MSE、MAE、MAPE分别降低4.71%、11.4%、22.6%，这表明Seq2seq模型能够较好地减小预测误差，但在预测初期数值波动较大。CEEMD-LSTM模型在进行CEEMD数据分解后减少了数据噪声，预测误差持续降低，缓解了预测初期数值波动较大的问题，与LSTM网络相比MSE、MAE、MAPE分别降低17.91%、25.73%、33.87%。CEEMD-Seq2seq经过编码器与解码器计算，较好地保留了数据的时间序列关系，与Seq2seq模型相比MSE、MAE、MAPE分别降低33.53%、40.03%、44.32%，但仍存在较大预测误差。在加入TCN网络进行特征提取后，CEEMD- TCN-LSTM模型、CEEMD-TCN-Seq2seq模型的预测误差呈现大幅度减小。CT-BiSeq2seq模型由于TCN的特征提取能力及解码器中Bi-LSTM网络的双向学习能力，减少了数据遗忘，相比于CEEMD-TCN- Seq2seq模型，MSE降低32.9%，MAE降低28.8%，MAPE降低17.7%，MSE、MAE、MAPE分别为0.657 4 元2/kg2、0.504 6元/kg、2.116 7%。在与各基准模型预测对比中取得了较优的效果。

因此，本文提出的CT-BiSeq2seq预测模型可有效降低了农产品价格序列非平稳、非线性特性带来的预测误差，预测值更精准。通过试验精确预测了测试集未来14个月（2021年12月至2022年2月）的白条猪肉价格，预测趋势图与原数据拟合良好。

3.4.2 滞后天数试验

预测时间序列问题通常会产生滞后性，即后几天的预测数据会映射出其前几天数据的特征，因此需要设置合理的滞后天数来进行预测，即用前几天的价格数据预测后一天的价格，减少预测误差。为验证CT-BiSeq2seq模型滞后天数为何值时价格的预测效果达到最优，设置了不同滞后天数的预测试验，其他参数与验证集得到的超参数保持一致，试验结果如表4所示。

表4 不同滞后天数的模型预测结果

由表4可得，滞后天数在9～13 d时，预测误差范围较小。滞后天数为11 d时，预测精度最高，MSE，MAE、MAPE值均达到最小，分别为0.657 4元2/kg2，0.504 6元/kg，2.116 7%。当滞后天数为5 d时，预测误差开始降低，当滞后天数为11 d时，预测误差达到最小，此后预测误差又开始增加，但整体的预测误差较小，说明本模型可较好用于农产品价格预测。这是由于农产品价格多遵循季节性变化规律，若直接设置季节性周期的滞后天数，滞后天数将较大，输入数据的序列长度会变长。较长的长序列数据在模型运行过程中容易遗忘靠前的序列数据，使得预测结果贴近靠后的序列数据，输入数据复杂度的提升并没有带来预测精度的提升，当滞后天数在13～15 d时损失值已经开始增大。因此拆分季节性周期的长度，缩短滞后天数可以尽可能保证模型学习数据间的规律，于是将滞后天数最大值设为15 d。但滞后天数太小时，模型容易陷入局部最优解，且不能充分学习时间序列的完整特征，当滞后天数处于3～7 d天时，损失值较大，其中3～5 d的损失值(MAE)均接近于1元/kg。最终确定最小滞后天数与最大滞后天数的中间值9～13 d为较为合适的滞后天数。

3.4.3 不同数据集检测

为了验证本模型在其他农产品数据集上预测的准确性，选取菠菜、苹果、鸡蛋三类常用农产品的价格数据进行预测，数据来源与3.1节相同，数据集时间范围取2021年1月1日至2022年2月28日农产品的每日价格，同时输入这3种数据的CEEMD价格分解数据、公众关注度、平均气温、化肥价格（尿素价格）、农产品价格等7维数据，具体如图12所示。

图12 不同农产品输入数据

将数据集划分为训练集、验证集、测试集，各部分所占比例分别为（6∶2∶2），模型的网络结构与3.3.4节保持一致，设置学习率分别为0.01、0.001、0.000 1，训练批次分别为32、64、128，训练周期为100、150、200，TCN、LSTM与Bi-LSTM的神经元个数按照高维度提取特征的思想分别设为32，64，128。选择滞后天数11 d。最终寻得较优超参数，当设置训练的批次大小为32，训练周期为100，学习率为0.001时损失误差最小。菠菜、苹果、鸡蛋3种农产品在测试集中的MSE、MAE、MAPE分别如表5所示，验证集与测试集的预测结果如图13所示。

表5 不同农产品的预测误差对比结果

由表5可得，3种农产品的MSE值均不超过0.65，因此本模型在不同种类的农产品价格预测上也有较高的准确性，同时在数据量变小时，预测误差仍然很低。根据图13可得，3种农产品的预测值基本接近实际值。具体分析，菠菜预测误差的MAPE值相对较大。经分析菠菜价格在2021年内的波动较大，苹果价格与鸡蛋价格波动较小，较大的价格波动导致菠菜价格的预测误差相对较大，苹果与鸡蛋的预测误差相对较小。

图13 菠菜、苹果、鸡蛋价格预测结果

由于各农产品价格具有不同的波动特点，因此对滞后天数的选择需要根据其特点进行设置。本文最后针对菠菜、苹果、鸡蛋3种农产品价格，在超参数不变的情况下，选择不同的滞后天数进行试验，结果如表6所示。结果发现菠菜与鸡蛋在滞后天数为11 d时预测误差达到最小，而苹果在滞后天数为7 d时预测误差达到最小。具体分析，针对价格波动较大的农产品，采用较大的滞后天数可以更完整的学习价格的变化规律；而对于价格波动较小的农产品，由于其价格前后趋势变化较小，选择较小的滞后天数就可以完成训练。

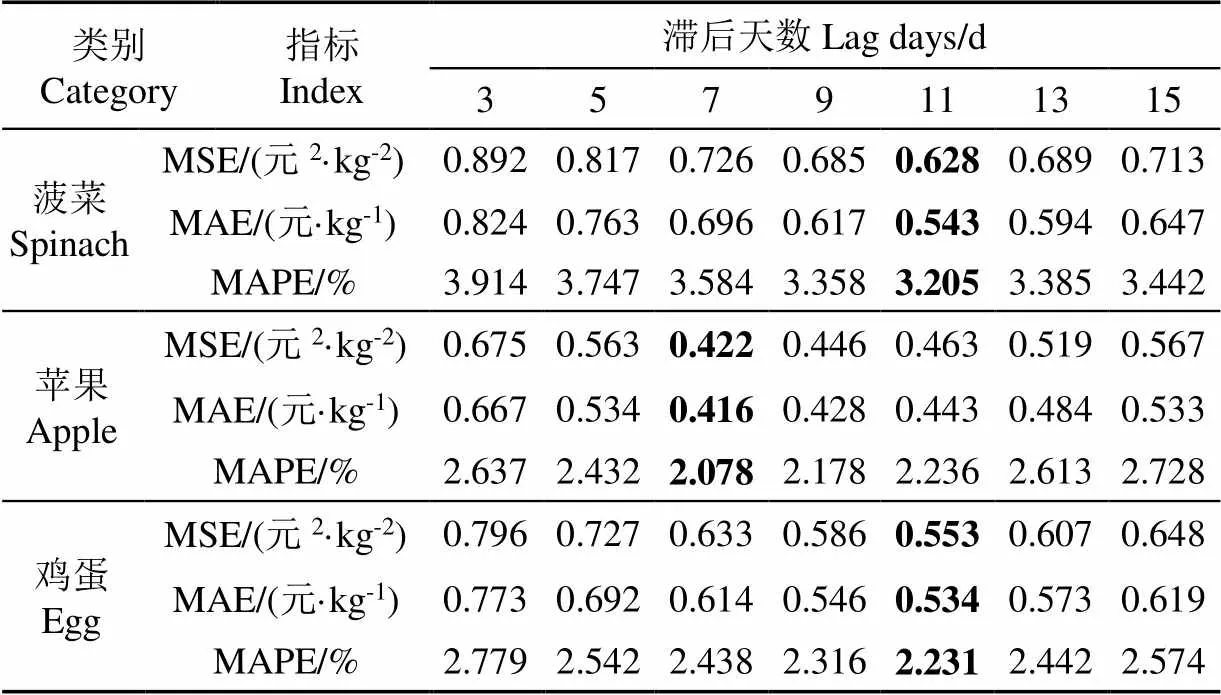
表6 不同农产品的滞后天数试验

4 结 论

本文结合信号分解和深度学习，按照分解-重构-提取-关联-输出的思想，提出了一种基于CT-BiSeq2seq模型的农产品价格预测方法，并对白条猪肉、菠菜、苹果、鸡蛋价格进行实证分析，得出以下结论。

1）本文提出的预测模型结合信号分解与深度学习的方法，经过分解-重构-提取-关联-输出5个步骤，对比其他组合预测模型，可较大幅度提高价格预测的准确性。其评价指标均方误差(MSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)的值在预测白条猪肉价格时分别可达到0.657 4元2/kg2、0.504 6元/kg、2.116 7%均维持在较小范围。并且在其他农产品数据集上也有较好的预测精度。这为解决农产品的预测问题提供跨学科融合的思路。

2）通过互补集合经验模态分解（Complementary Ensemble Empirical Mode Decomposition，CEEMD）将复杂数据转化为多个简单数据，再引入平均气温、养殖成本、群众关注度等数据进行多维度的训练。CEEMD-LSTM模型的MSE、MAE、MAPE相比于LSTM网络分别降低17.91%、25.73%、33.87%；CEEMD-Seq2seq模型的MSE、MAE、MAPE相比于Seq2seq模型分别降低33.53%、40.03%、44.32%，预测误差减小，这证明了数据分解对降低损失误差的有效性。其中分解的高频项代表常规事件对整体价格走势的影响，其对农产品价格的波动影响较小。残差项反映农产品价格的内在长期走势，主要由供求关系决定。低频项代表重大事件对农产品价格走势的影响，其对农产品价格的波动影响较大。保证残差项（供求关系）平衡与健全重大事件预警体系对防止农产品价格波动有重大意义。

3）在农产品价格预测中滞后天数的选择较为关键，由本文可得，价格波动大的农产品宜选择较大的滞后天数，价格波动小的农产品宜选择较小的滞后天数。

本文提出的CT-BiSeq2seq模型具有良好的预测性能和泛化能力，可以为农产品价格的预测提供参考依据。

[1] 马宏阳，赵霞. 中国小宗农产品价格波动特征的实证分析—以大蒜为例[J]. 农业技术经济，2021(6)：33-48.

Ma Hongyang, Zhao Xia. An empirical analysis of the price fluctuation characteristics of China's small agricultural products[J]. Journal of Agrotechnical Economics, 2021(6): 33-48. (in Chinese with English abstract)

[2] Weng Y C, Wang X J, Hua J, et al. Forecasting horticultural products price using ARIMA model and neural network based on a large-scale data set collected by web crawler[J]. Ieee Transactions on Computational Social Systems, 2019, 6(3): 547-553.

[3] 张贵生，张信东. 基于微分信息的ARMAD-GARCH股价预测模型[J]. 系统工程理论与实践，2016，36(5)：1136-1145.

Zhang Guisheng, Zhang Xindong. A differential-information based ARMAD-GARCH stock price forecasting model[J]. Systems Engineering-Theory & Practice, 2016, 36(5): 1136-1145. (in Chinese with English abstract)

[4] 刘慧，李宁辉. 我国小宗农产品价格波动趋势及其预测：以绿豆为例的分析[J]. 价格理论与实践，2012(6)：57-58.

Liu Hui, Li Ninghui. Price fluctuation trend and forecast of small agricultural products in China: Taking mung bean as an example[J]. Price: Theory & Practice, 2012(6): 57-58. (in Chinese with English abstract)

[5] 熊涛，鲍玉昆. 基于动态模型平均的大豆期货价格预测研究[J]. 中国管理科学，2020，28(5)：79-88.

Xiong Tao, Bao Yukong. Soybean future price forecasting based on dynamic model averageing[J]. Chinese Journal of Management Science, 2020, 28(5): 79-88. (in Chinese with English abstract)

[6] 贾宝疆. 中国主要农产品销售价格预测[J]. 统计与决策，2014(20)：100-102.

Jia Baojiang. Sales price forecast of main agricultural products in China[J]. Statistics & Decision, 2014(20): 100-102. (in Chinese with English abstract)

[7] 崔畅，李国伟. 我国农产品价格的结构变化特征及影响因素分析[J]. 数理统计与管理，2019，38(1)：1-15.

Cui Chang, Li Guowei. Analysis of structural change characteristics and influencing factors of agricultural product prices[J]. Journal of Applied Statistics and Management, 2019, 38(1): 1-15. (in Chinese with English abstract)

[8] 唐振鹏，吴俊传，张婷婷，等. 基于二次分解和集成学习的粮食期货价格预测研究[J]. 系统工程理论与实践，2021，41(11)：2837-2849.

Tang Zhenpeng, Wu Junchuan, Zhang Tingting, et al. Research on grain futures price forecasting based on secondary decomposition and ensemble learning[J]. Systems Engineering-Theory & Practice, 2021, 41(11): 2837-2849. (in Chinese with English abstract)

[9] 孙少杰，吴门新，庄立伟，等. 基于CNN卷积神经网络和BP神经网络的冬小麦县级产量预测[J]. 农业工程学报，2022，38(11)：151-160.

Sun Shaojie, Wu Menxin, Zhuang Liwei, et al. Forecasting winter wheat yield at county level using CNN and BP neural networks[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(11): 151-160. (in Chinese with English abstract)

[10] 王滢艺，徐胜祥，赵永存，等. 基于VNIR和机器学习算法的原状土剖面Cu含量预测[J]. 农业工程学报，2022，38(7)：336-344.

Wang Yingyi, Xu Shengxiang, Zhao Yongcun, et al. Prediction of Cu concentrations in intact soil profiles based on VNIR and machine learning algorithms[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(7): 336-344. (in Chinese with English abstract)

[11] 李哲敏，许世卫，崔利国，等. 基于动态混沌神经网络的预测研究：以马铃薯时间序列价格为例[J]. 系统工程理论与实践，2015，35(8)：2083-2091.

Li Zhemin, Xu Shiwei, Cui Liguo, et al. Prediction study based on dynamic chaotic neural network Taking potato time: series prices as an example[J]. Systems Engineering-Theory & Practice, 2015, 35(8): 2083-2091. (in Chinese with English abstract)

[12] 王泽鹏，陈晓燕，庞涛，等. 一种基于改进时间卷积网络的生猪价格预测方法[J]. 中国农业大学学报，2021，26(12)：137-144.

Wang Zepeng, Chen Xiaoyan, Pang Tao, et al. A hog price prediction method based on improved temporal convolutional network[J]. Journal of China Agricultural University, 2021, 26(12): 137-144. (in Chinese with English abstract)

[13] Sterkenburg T F, Grunwald P D. The no-free-lunch theorems of supervised learning[J]. Synthese, 2021, 199(3/4): 9979-10015.

[14] Gambella C, Ghaddar B, Naoum-Sawaya J. Optimization problems for machine learning: A survey[J]. European Journal Of Operational Research, 2021, 290(3): 807-828.

[15] 刘双印，黄建德，徐龙琴，等基于PCA-SVR-ARMA的狮头鹅养殖禽舍气温组合预测模型[J]. 农业工程学报，2020，36(11)：225-233.

Liu Shuangyin, Huang Jiande, Xu Longqin, et al. Combined model for prediction of air temperature in poultry house for lion-head goose breeding based on PCA-SVR-ARMA[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(11): 225-233. (in Chinese with English abstract)

[16] 徐映梅，陈尧. 季节ARIMA模型与LSTM神经网络预测的比较[J]. 统计与决策，2021，37(2)：46-50.

Xu Yingmei, Chen Yao. Comparison between seasonal ARIMA model and LSTM neural network forecast[J]. Statistics & Decision, 2021, 37(2): 46-50. (in Chinese with English abstract)

[17] 孙少龙，魏云捷，汪寿阳. 基于分解-聚类-集成学习的汇率预测方法[J]. 系统工程理论与实践，2022，42(3)：664-677.

Sun Shaolong, Wei Yunjie, Wang Shouyang. Exchange rates forecasting method with decomposition-clustering-ensemble learning approach[J]. Systems Engineering-Theory & Practice, 2022, 42(3): 664-677. (in Chinese with English abstract)

[18] 欧阳红兵，黄亢，闫洪举. 基于LSTM神经网络的金融时间序列预测[J]. 中国管理科学，2020，28(4)：27-35.

Ouyang Hongbin, Huang Kang, Yan Hongju. Prediction of financial time series based on LSTM neural network[J]. Chinese Journal of Management Science, 2020, 28(4): 27-35. (in Chinese with English abstract)

[19] 朱帮助，魏一鸣. 基于GMDH-PSO-LSSVM的国际碳市场价格预测[J]. 系统工程理论与实践，2011，31(12)：2264-2271.

Zhu Bangzhu, Wei Yiming. Carbon price prediction based on integration of GMDH, particle swarm optimization and least squares support vector machines[J]. Systems Engineering-Theory & Practice, 2011, 31(12): 2264-2271. (in Chinese with English abstract)

[20] 王书平，朱艳云. 基于多尺度分析的小麦价格预测研究[J]. 中国管理科学，2016，24(5)：85-91.

Wang Shuping, Zhu Yanyun. Forecasting of wheat price based on multi-scale analysis[J]. Chinese Journal of Management Science, 2016, 24(5): 85-91. (in Chinese with English abstract)

[21] 王珏，齐琛，李明芳. 基于SSA-ELM的大宗商品价格预测研究[J]. 系统工程理论与实践，2017，37(8)：2004-2014.

Wang Yu, Qi Chen, Li Mingfang. Prediction of commodity prices based on SSA-ELM[J]. Systems Engineering-Theory & Practice, 2017, 37(8): 2004-2014. (in Chinese with English abstract)

[22] 方雪清，吴春胤，俞守华，等. 基于EEMD-LSTM的农产品价格短期预测模型研究[J]. 中国管理科学，2021，29(11)：68-77.

Fang Xueqing, Wu Chunyin, Yu Shouhua, et al. Research on Short-term forecast model of agricultural product price based on EEMD-LSTM[J]. Chinese Journal of Management Science, 2021, 29(11): 68-77. (in Chinese with English abstract)

[23] 刘雪，刘锦涛，李佳利，等. 基于季节分解和长短期记忆的北京市鸡蛋价格预测[J]. 农业工程学报，2020，36(9)：331-340.

Liu Xue, Liu Jintao, Li Jiali, et al. Egg price forecasting in Beijing market using seasonal-trend decomposition procedures based on seasonal decomposition and long-short term memory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(9): 331-340. (in Chinese with English abstract)

[24] 赵凤展，郝帅，张宇，等. 基于变分模态分解-BA-LSSVM算法的配电网短期负荷预测[J]. 农业工程学报，2019，35(14)：190-197.

Zhao Fengzhan, Hao Shuai, Zhang Yu, et al. Short-term load forecasting for distribution transformer based on VMD-BA-LSSVM algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(14): 190-197. (in Chinese with English abstract)

[25] Fu Z Y, Long J J, Chen W Q, et al. Reliability of the prediction model for landslide displacement with step-like behavior[J]. Stochastic Environmental Research And Risk Assessment, 2021, 35(11): 2335-2353.

[26] 杨静凌，唐国强，张建文. 基于CEEMD-Elman-Adaboost组合模型的国际原油价格预测研究[J]. 重庆理工大学学报(自然科学)，2021，35(3)：260-267.

Yang Jingling, Tang Guoqiang, Zhang Jianwen. Research on prediction of international crude oil price based on CEEMD-Elman-Adaboost combination model[J]. Journal of Chongqing University of Technology (Natural Science), 2021, 35(3): 260-267. (in Chinese with English abstract)

[27] Zanghieri M, Benatti S, Burrello A, et al. Robust real-time embedded EMG recognition framework using temporal convolutional networks on a multicore IoT processor[J]. Ieee Transactions On Biomedical Circuits And Systems, 2020, 14(2): 244-256.

[28] Yang H S, Ding K Q, Qiu R C, et al. Remaining useful life prediction based on normalizing flow embedded Sequence-to-Sequence learning[J]. Ieee Transactions On Reliability, 2021, 70(4): 1342-1354.

[29] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553):436–444

[30] 冯建英，吴丹丹，王博，等. 中文在线评论文本分析对生鲜农产品电商影响研究综述[J]. 农业机械学报，2021，52(S1)：504-512.

Feng Jianying, Wu Dandan, Wang Bo, et al. Online comments analysis and its application research progress in e-commerce of fresh agricultural products[J]. Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(S1): 504-512. (in Chinese with English abstract)

[31] Bohra N, Bhatnagar V. Group level social media popularity prediction by MRGB and Adam optimization[J]. Journal of Combinatorial Optimization, 2021, 41(2): 328-347.

[32] 苏娟，方舒，刘博，等. 基于模态组合的短期负荷预测方法[J]. 农业工程学报，2021，37(14)：186-196.

Su Juan, Fang Shu, Liu Bo, et al. Short term load prediction method based on modal combination[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(14): 186-196. (in Chinese with English abstract)

Agricultural product price prediction based on signal decomposition and deep learning

Wang Runzhou, Zhang Xinsheng※, Wang Minghu

(,,710055,)

A stable price of agricultural products is of great significance to the social economy and agricultural development in recent years. But, it is difficult to accurately predict the agricultural product prices, due to the non-stationary, non-linear, and high volatility. In this study, a novel prediction model of the decomposition-reconstruction-extraction-associated-output agricultural product price (CT-BiSeq2seq) was proposed using signal decomposition and deep learning. The multi-dimensional data was added to improve the model prediction accuracy, such as the average temperature, and fertilizer cost (price of pig formula feed and urea). Firstly, the original price series were divided into simple ones using the complementary ensemble empirical mode decomposition (CEEMD). Secondly, the original price series was reconstructed into the high-frequency, low-frequency, and residual items, according to the Pearson correlation coefficients and the decomposed subsequence. Thirdly, the data features of the reconstructed sequence were extracted via a temporal convolutional network (TCN). The 7-dimensional data was input to extract the influencing factors on the price of agricultural products. The output steps were similar to the input ones. Fourthly, a Biseq2seq model was constructed with an encoder and a decoder. A bi-directional Long Short-Term Memory network (Bi-LSTM) was introduced into the encoder to strengthen the global correlation between sequence data. Finally, the LSTM network was introduced into the decoder to output the predictive value of the number of steps. Taking the pork price of the Fengtai District wholesale market in Beijing of China for empirical analysis, the prediction performance of the CT-BiSeq2seq model was remarkably better than the rest benchmark models, indicating the number of lags reached the optimal in 11 days. The mean square error (MSE), the mean absolute error (MAE), and the mean absolute percentage error (MAPE) were 0.657 4 rmb2/kg2、0.504 6 rmb/kg、2.116 7%, respectively. Furthermore, the few-day lag cannot fully reflect the overall characteristics of agricultural product prices, where there was easy access to fall into the local optimum. Once the lag days were too long, overfitting was easy to occur, leading to low prediction accuracy. An accurate and stable prediction was also achieved in other datasets. The MSEs of spinach, apple, and egg were 0.627 7 RMB2/kg2, 0.463 2 RMB2/kg2, and 0.552 6 RMB2/kg2, respectively, while the MAEs were 0.543 1 rmb/kg, 0.442 5 rmb/kg, and 0.533 9 rmb/kg, respectively, and the MAPEs were 3.204 7%, 2.236 1% and 2.231 4%, respectively. Therefore, the agricultural products with large price fluctuations were suitable for the large lag steps, whereas, the small price fluctuations were suitable for the small lag steps. A large number of lag days were completely learned from the trend in large price changes. The short lag days were used to fit the time sequence in the smaller price changes, due to the relatively stable trend of price change. Specifically, the prices of spinach and eggs fluctuated greatly in the data range, where the loss error reached the minimum over the 11 lag days, respectively. By contrast, the price of Apples fluctuated less over the 7 lag days. This model can provide a strong reference to forecast the price fluctuation of agricultural products.

agricultural price; price forecast; complementary ensemble empirical mode decomposition; temporal convolutional network; bi-directional sequence to sequence model; long-short term memory

10.11975/j.issn.1002-6819.2022.24.028

F304.2；TP301.6

A

1002-6819(2022)-24-0256-12

王润周，张新生，王明虎. 基于信号分解和深度学习的农产品价格预测[J]. 农业工程学报，2022，38(24)：256-267.doi：10.11975/j.issn.1002-6819.2022.24.028 http://www.tcsae.org

Wang Runzhou, Zhang Xinsheng, Wang Minghu. Agricultural product price prediction based on signal decomposition and deep learning[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(24): 256-267. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.24.028 http://www.tcsae.org

2022-08-26

2022-10-26

国家自然科学基金(41877527)；陕西省重点产业创新链(群)-工业领域项目(2022ZDLGY06-04)；陕西省教育厅重点科学研究计划项目(20JT033)

王润周，博士生，研究方向为智能信息处理与模式识别。Email：wangrunzhou@xauat.edu.cn

张新生，博士，教授，研究方向为机器学习、智能信息处理等。Email：xinsheng.zh@outlook.com