模拟退火算法求解的道路网络分配方法
许修权,廉 冠,张曼婷
(桂林电子科技大学建筑与交通工程学院,广西 桂林 541004)
0 引言
在交通规划四阶段的交通分配阶段,要对交通流量进行分配,就要考虑到某条路径的时间阻抗。对于路段行驶时间的修正,可以根据行驶时间和路段交通量之间的关系,即路阻函数确定。最为常见的路阻函数是美国联邦公路局函数(BPR函数)其具体公式如下:
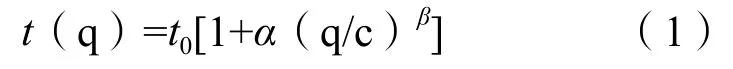
式中:t(q)为流量为q时路段的行程时间;t0为路段的自由行程时间;c为路段的实际通行能力;α,β为回归系数,α建议取值=0.15,β建议取值=4。
BPR路阻函数是本文函数关系构造的基础,通过BPR函数得到每条道路行驶时间和路段交通负荷之间的函数关系。
1 系统平均行程时间函数的构造
假设A和B之间有n条道路分别记作Link1、Link2、Link3…Linkn,每条道路的实际通行能力为C1、C2、C3…Cn,道路的自由通行时间为t1、t2、t3…tn,A和B之间的交通总量为C。将每条道路分配的交通量的百分比分别记作x1、x2、x3…xn-1、,则
每条道路的路阻函数为:
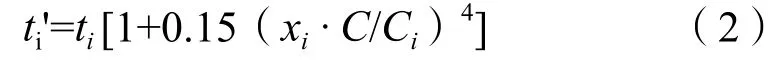
系统平均行程时间为:
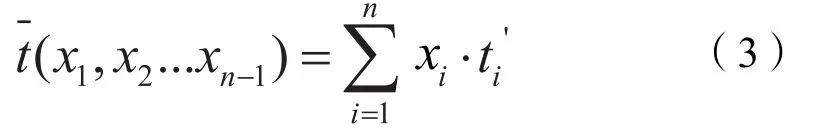
通过分析得,系统的平均行程实际是一个n-1元的多元函数,只要求得该函数取得最小值时的自变量,就能得到道路网络的最优分配。
结合实际意义,对函数的解的可行域进行分析:
(1)x1、x2、x3…xn-1均应该∈[0,1];取0时,此道路不分配任何交通量,取1时,所有交通量分配于此道路。
(3)∀x1、x2、x3…xn-1的组合都应该小于等于1(不难理解当条件1、2均满足时,条件3也满足)
通过上述分析不难理解,当n=3时,解的可行域为三角形;当n=4时,解的可行域为三棱锥;当n比较大时解的可行域就是更加复杂的高纬度的图形。
下面对函数的构造进行举例说明:

图1 交通量、行程时间分配图Fig.1 Map of traffic volume and travel time allocation
假设A和B之间有三条道路且道路网络交通的分配满足Wardrop第一原理、第二原理。Link1路段的实际通行能力为1 200,道路自由通行时间为1。Link2路段的实际通行能力为1 500,道路自由通行时间为1.2。Link3路段的实际通行能力为1 000,道路自由通行时间为1.5。
A与B之间产生的交通量为3 000。如果令Link1分配的交通量的百分比为自变量x,Link2分配的交通量的百分比为自变量y,显然z分配的交通量为1-x-y;那么不难构造出三条道路的路阻函数。
Link1的路阻函数:
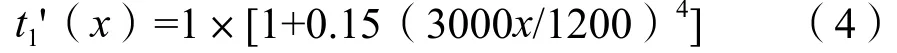
Link2的路阻函数:
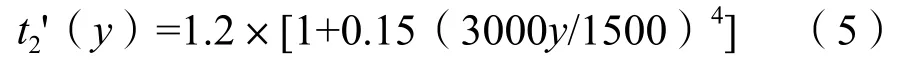
Link3的路阻函数:
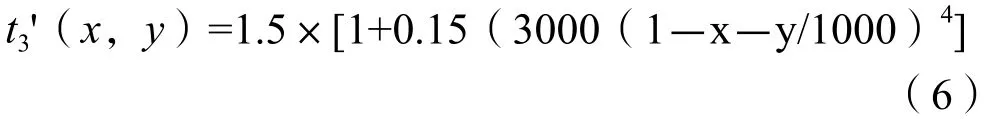
很容易得到整个系统的平均行程时间为:
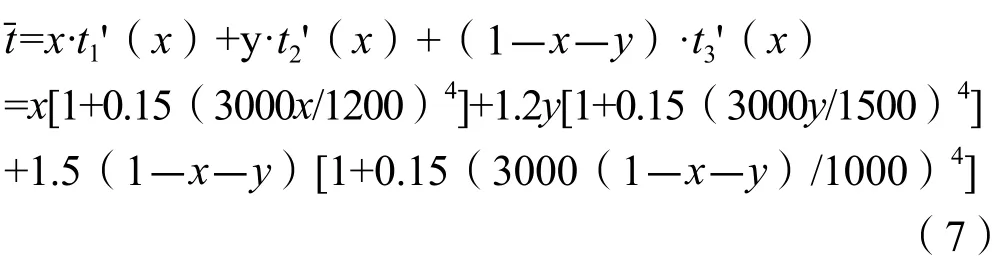
至此,得到整个系统的平均行程时间的函数表达式,做出该图形,并求得此图形的最小值点。
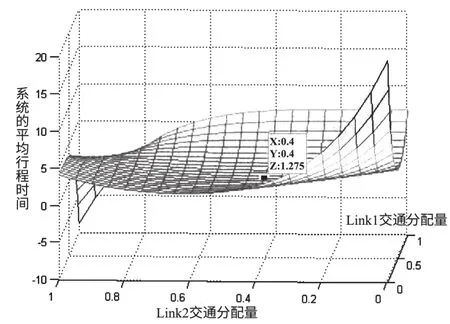
图2 系统平均行程时间图Fig.2 Map of system average travel time
由图不难找出最小值点(图像范围应该限制于x+y≤1内的三角形)为(0.4,0.4,1.275),即Link1、Link2分配1 200的交通量,Link3分配600的交通量。此时系统内平均行程时间最短为1.275。
2 系统平均行程时间的解法——模拟退火算法
模拟退火算法(Simulated Annealing,SA)是一种全局优化方法,它是基于Monte-Carlo迭代求解策略的一种随机寻优算法,其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法,理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用。
通过道路平均行程时间函数的构造,能够得到道路网络的最优分配方式,但通过一般求全导数的方式求函数最小值是极其复杂的,特别是当自变量较多的时候,其结果实际是多维空间的一个点,计算难度很大。通过模拟退火智能算法来求道路平均行程时间函数的最优解。
2.1 模型构建
对于一个目标函数为f(x)、自变量为x的n维极小化问题,设fk,fk+1分别为目标函数在第k次和k+1次的迭代值,即fk=f(xk),fk+1=f(xk+1)。若fk>fk+1,则接受xk+1为当前点,作为下一次迭代的初值继续进行迭代运算,直到满足收敛结束条件;若fk≤fk+1,则xk+1可能被接受也可能被拒绝,接受的概率为Boltzmann概率p。
Boltzmmann概率p也称为接受概率,定义为:
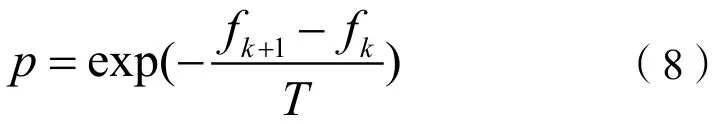
其中,T是控制参数,在迭代寻优过程中,T必须缓慢减少,控制参数变化太快,会使优化陷入局部极值点。
2.2 模型介绍
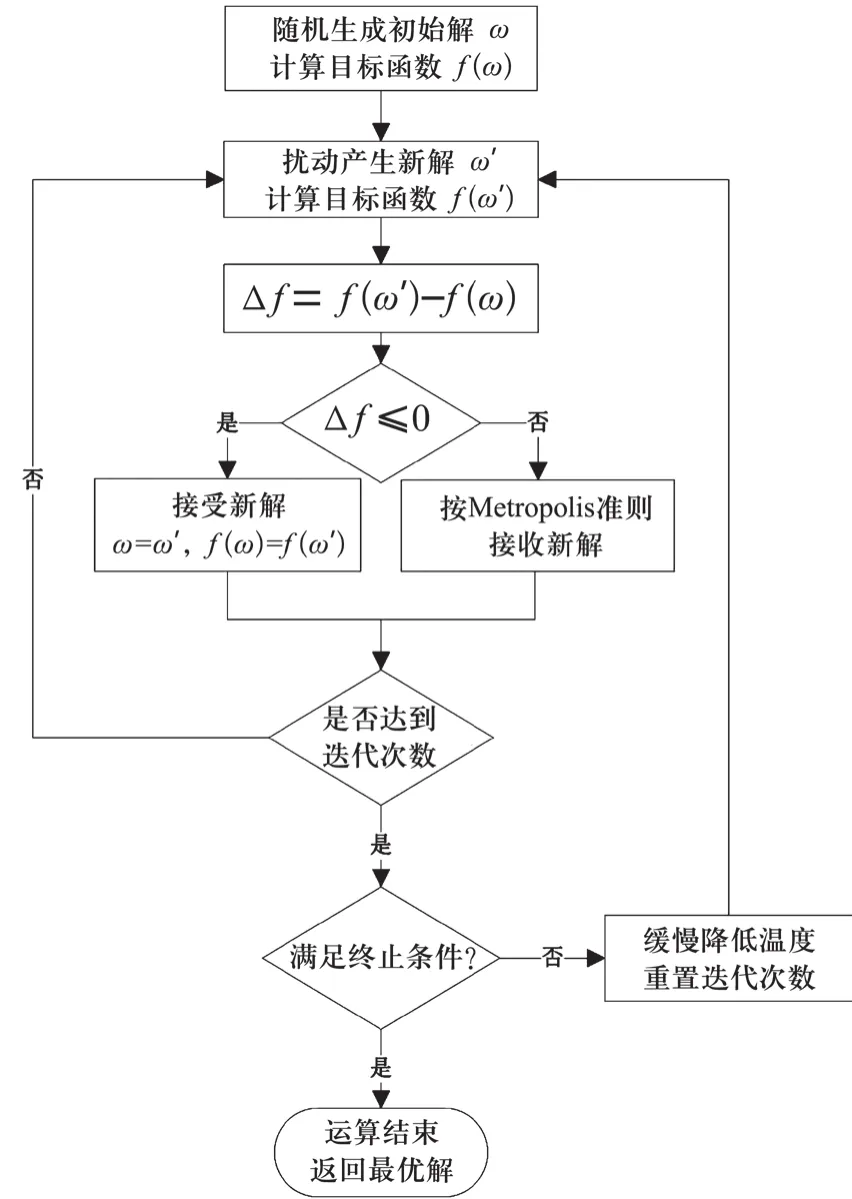
图3 系统迭代优化步骤流程框架Fig.3 System iterative optimization step process framework
模拟退火的基本思想:
(1)初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点),每个T值的迭代次数L;
(2)对k=1,…,L做第(3)至第6步;
(3)产生新解S′;
(4)计算增量ΔT=C(S′)-C(S),其中C(S)为评价函数;
(5)若ΔT<0则接受S′作为新的当前解,否则以概率exp(-ΔT/T)接受S′作为新的当前解;
(6)如果满足终止条件则输出当前解作为最优解,结束程序。
2.3 举例分析
使用模拟退火算法求解系统平均行程时间函数:
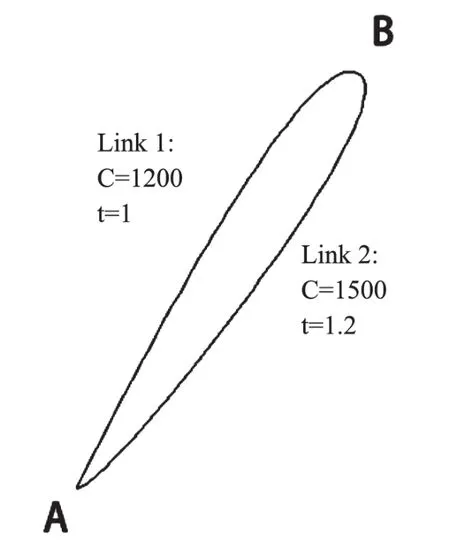
图4 求解路径平均行程时间示例图Fig.4 Example diagram of the average travel time of the solution path
我们举一个简单的例子假设A和B之间有两条道路,且道路网络交通的分配满足Wardrop第一原理、第二原理。Link1路段的实际通行能力为1 200,道路自由通行时间为1。Link2路段的实际通行能力为1 500,道路自由通行时间为1.2。
A与B之间的出行量为2 000辆/h。令A与B之间的出行量中A承担的百分比为自变量x,则可以构造出Link1和Link2的BPR路阻函数。
Link1的路阻函数:
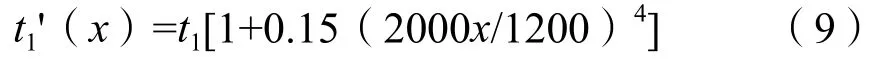
Link2的路阻函数:
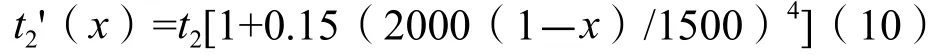
得到整个系统的平均行程时间为:
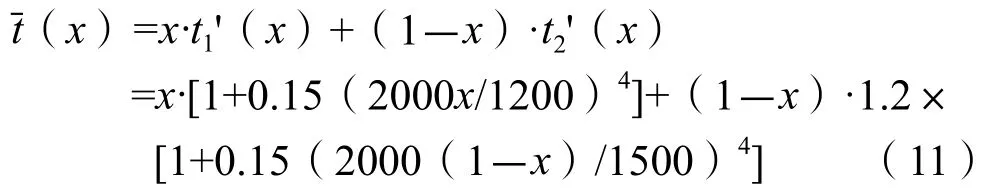
可以通过求导等方法得到整个系统的最优值,但是当A与B之间有多个道路时,就需要求多元函数的最优值。因此直接利用matlab中模拟退火算法工具箱求全局优化方法,得到结果如图5所示。
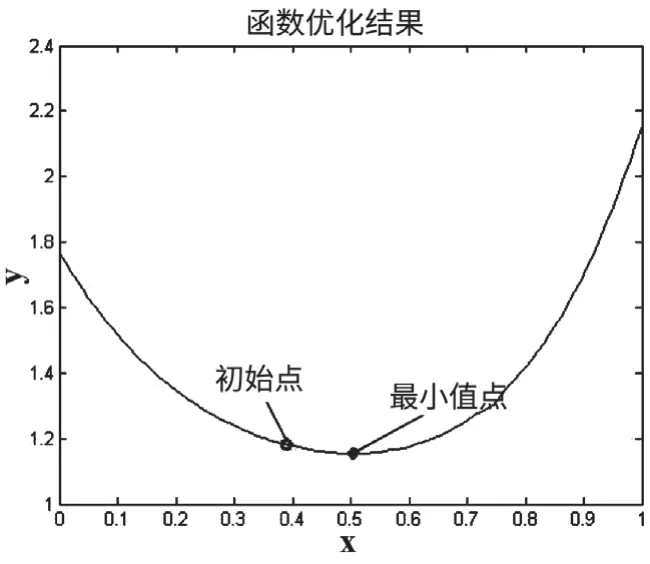
图5 函数优化结果示例图Fig.5 Example graph of function optimization results
优化结果显示,取x=0.51时,系统的平均行程时间最少,为1.153,即Link1分配的交通量为1 020。
Link2分配的交通量为980时得到最优的分配方式,这时系统的平均行程时间为1.153。
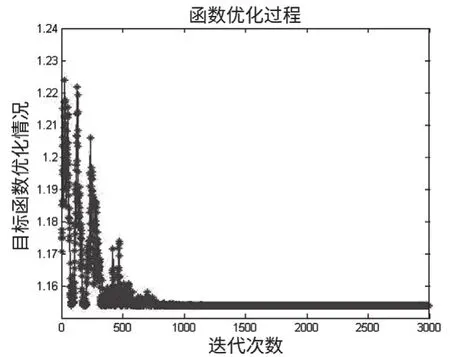
图6 目标函数迭代优化图Fig.6 Graph of objective function iterative optimization
经过3 000次的迭代运算,在约800次的运算之后函数收敛至1.153位置。
2.4 模型的对比
至此已经通过案例对利用BPR路阻函数求解平衡的交通分配问题有了一定认识,与其他交通分配模型相比,此模型具有以下优势。
与容量限制-多路径交通分配方法比较:
采用容量限制-多路径交通分配方法先将交通量分配为k个分交通量,然后分k次用多路径分配模型分配交通量。多路径分配模型采用Logit型的路径选择模型进行计算。

利用容量限制-多路径交通分配方法对刚才的例子进行计算(迭代次数取4次,每次交通量均为500;分配参数θ=3.00)计算结果见表1。

表1 迭代求解结果Tab.1 Iterative solution result
分配后系统的平均路阻为1.196 9,大于模拟退火算法求得的1.153。显然模拟退火算法计算结果优于容量限制-多路径交通分配方法。
(1)与非平衡交通分配方法的对比
非平衡模型具有结构简单、概念明确、计算简便等优点,也得到了广泛应用,但无法取得最优解是这类分配方法的致命缺点;而本文的方法则通过随机类全局优化算法求得了最优的结果。不可否认,非平衡模型具有一定的优势,比如多路径交通分配方法一般取5次就能满足精度要求,而本文的方法在经过约800次迭代后才完成了计算的收敛。
(2)固定需求分配方法,弹性需求平衡分配类模型的对比
这类算法利用线性规划的方法通过Frank-wolfe算法求得最优解,但由于Frank-wolfe算法不能求解非线性规划问题,非线性规划问题并没有一般的通用解法。所以这类算法不能给出一般解法,依然具有一定的局限性。
2.5 模型的改进
通过与其他交通平衡方法的比较,发现该模型的主要缺点是迭代次数多,计算量大,为了加快计算的收敛,本文提出以下建议:
(1)适当增加概率函数中参数T(控制参数T不能过大,否则优化会陷入局部极值点)。
(2)初始点的确定可以通过非平衡交通分配方法确定,合理的初始点能够有效地减少迭代次数。
系统平均行程时间的准确性改进:
系统平均行程时间实质是由BPR路阻函数推导求得,本文中均采用了BPR路阻函数中的推荐值,即α=0.15,β=4。在更复杂的情况下,可以根据实际的需要修改t(q)=t0[1+α(q/c)β]中的回归系数α,β,以获得更加准确的路阻函数和系统平均行程时间。
模型经改进后迭代情况:当t位于0.950 0~0.996 0范围时,路阻收敛于1.153 916 944,收敛情况较好,图7为优化结果。
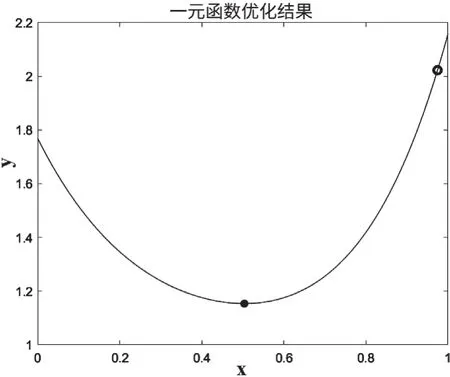
图7 一元函数优化结果Fig.7 Unary function optimization results
优化结果显示,取x=0.51时,系统的平均行程时间最少,为1.153。
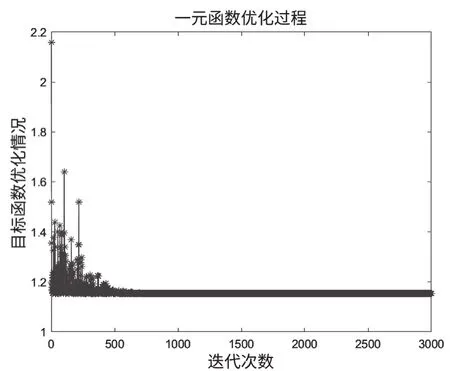
图8 一元函数优化过程Fig.8 Unary function optimization process
3 000次迭代运算后,约500次迭代后函数收敛于1.153 916 944位置。
3 结论
本文应用模拟退火算法,通过BPR路阻函数得到道路行驶时间与交通负荷之间的关系,构建系统平均行程时间函数,通过对函数带入参数进行迭代优化得到了系统平均行程最短时间以及相应的道路网络交通分配,优化结果较优,令人满意。

