TRD工法在广州地区复杂地层中的承载变形性状分析

沈 捷

（广州地铁集团有限公司 广州 510330）

0 引言

TRD（Trench cutting Re-mixing Deep wall）工法，又称等厚度水泥土搅拌地下连续墙工法，是2009年从日本引进至国内的一种利用锯链式切削箱连续施工等厚水泥土搅拌墙的施工技术，其成墙工艺为首先将链锯型切削刀具插入地基，掘削至墙体设计深度，然后注入固化剂使其在整个墙体设计深度范围内与原位土体进行充分的搅拌混合，并持续横向掘削、搅拌，水平推进，构筑成连续的等厚度水泥土搅拌地下连续墙［1-2］。

TRD 工法构建的等厚度水泥土搅拌地下连续墙与内插型钢相结合可作为基坑型钢水泥土搅拌地下连续墙围护结构体系［3-4］。在型钢水泥土搅拌地下连续墙组合结构体系，水泥土主要作为止水帷幕、约束H 型钢发生侧向变形而失稳［5-7］；H 型钢则因其刚度和抗拉压强度高而作为主要的受力构件。尽管内插型钢TRD工法构造相对简单，然而对于两种刚度差极大的材料组合体系，其力学响应机理复杂，特别是其承载变形特性以及型钢和水泥土相互作用与传统的桩墙支护体系存在差异，研究尚滞后于工程实践［8-11］。为此，本文以广州市番禺区广州地铁某停车场U 型槽基坑（广州市首个采用TRD 工法的基坑工程）为工程依托，采用Midas∕GTS 有限元软件建立精细的三维有限元模型，对TRD工法型钢水泥土搅拌地下连续墙围护结构的承载和变形特性进行分析和研究，总结出相关经验，为TRD工法在大湾区尤其是广州地铁建设项目的推广和应用打下坚实的理论基础。

1 工程概况

1.1 基坑概况

某停车场位于番禺大道北以东，市南路以北，草龙沙河二街以西的地块内，车场呈东西向布置。地块长约990 m，宽约220 m，停车场永久占地面积约20 公顷。该选址现状为田地、厂房及少量的村民住宅。综合楼位于停车场南侧，现状地面标高约为4.6～7.9 m，场地要求初步平整标高为5.5 m。出入场线洞口里程为RDK2+840.12，出洞口后设置U型槽，U型槽深度为0～11.3 m。出入场线U型槽段位于停车场用地红线以内，南侧距离市南路仅4.95 m，周边已进行征地拆迁，无已建建筑物。

1.2 水文地质概况

停车场地质相对复杂，由上到下依次为0.3～2.5 m填土层、0.6～5.1 m 淤泥及淤泥质土层、1.0～5.1 m 淤泥质粉细砂、0.5～8.05 m 粉质黏土层、0.9～7.4 m 残积土层、0.7～7.2 m 泥质粉砂岩全强风化层、基岩为泥质粉砂岩层，地层分布不均。基坑开挖范围主要为填土、淤泥、粉质粘土、淤泥质粉细砂层等。基坑坑底主要为土层，局部为全风化泥质粉砂岩土。因此，场地的地质条件复杂，土质情况较差，软弱土层最后深度达10.0 m，透水粉砂层达5.0 m，对围护结构的刚度、止水性和施工工期均有严格的要求。

2 三维有限元模型的建立

2.1 基本情况

基坑开挖深度11.3 m，顶部设置0.8 m×1.2 m C30混凝土冠梁，设置两道支撑，第一道采用0.8 m×0.8 m混凝土内支撑，水平间距9.0 m；第二道采用φ609壁厚16 mm 钢支撑，水平间距3.0 m，与第一道混凝土内支撑竖向间距为3.85 m，典型剖面如图1 所示。TRD 等厚度水泥土搅拌地下连续墙深度14.5 m，内插HN700×300×13×24H型钢。有限元数值模拟分别分析TRD 墙体厚度、抗压强度、内插H 型钢水平间距和内插型钢插入深度4个因素对支护效果的影响。三维有限元模型取90.2 m×16.0 m×25.0 m 的区域，上部为自由边界，底部全约束，各侧边限制向基坑方向的水平位移，三维有限元模型如图2所示。

图1 基坑支护结构剖面（A段）Fig.1 Profile of Foundation Pit Support Structure（A）（mm）

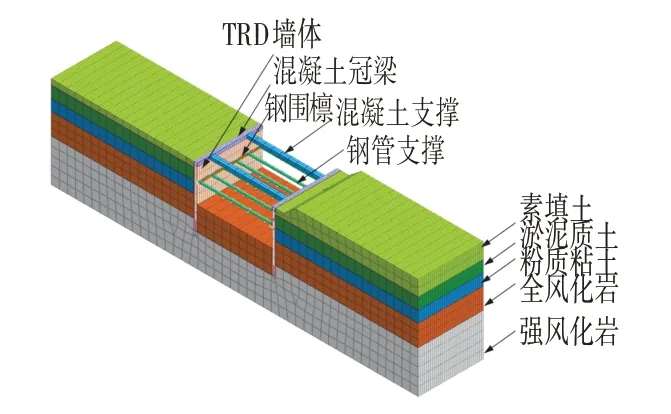
图2 Midas/GTS有限元模型Fig.2 Midas/GTS Fem Model

2.2 基本假定

该模型建立的基本假定主要如下：

⑴土体本构模型采用莫尔-库仑本构模型，支护结构体系本构模型采用线性弹性模型，各材料的物理力学参数如表1所示。

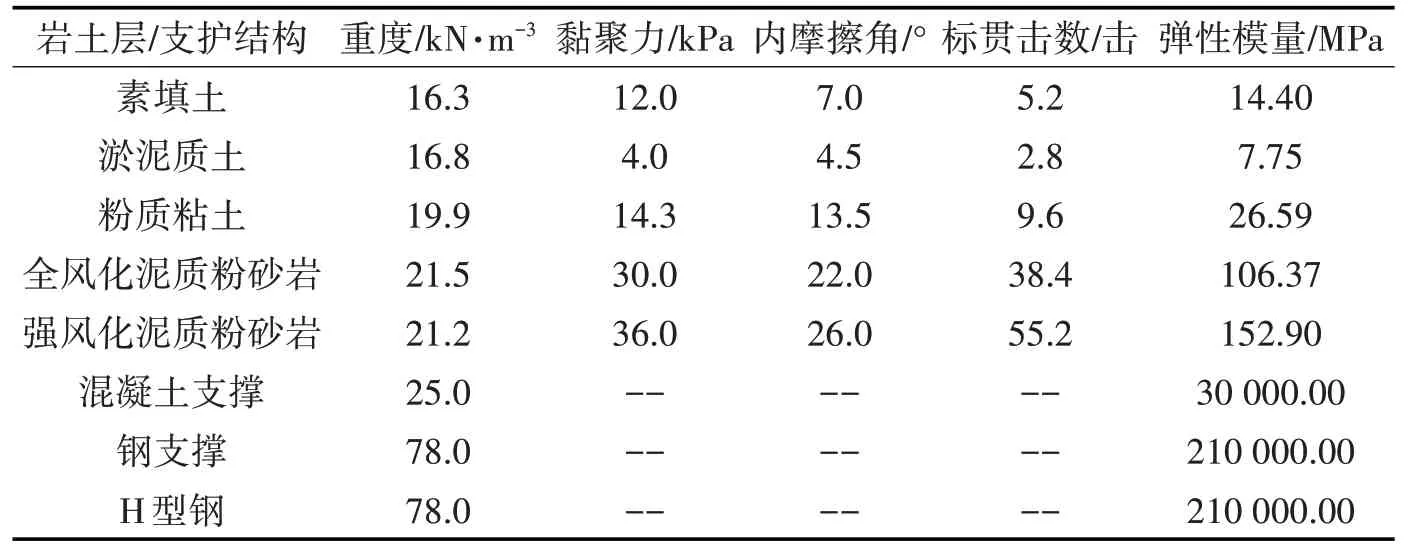
表1 有限元模型各材料物理力学参数Tab.1 Physical Parameters of Materials in Finite Element Model

⑵假定各土层都为成层均质水平分布；

⑶不考虑地下水在基坑开挖过程中的影响；

⑷不考虑开挖过程中的时间因素。

3 数值模拟结果与分析

3.1 模拟结果

3.1.1 TRD墙体厚度对支护结构体系承载变形性状影响

Midas∕GTS 有限元模型中，分别设置TRD 墙体厚度为0.85 m、1.2 m 和1.4 m，TRD 墙体的水泥土无侧限抗压强度设计值为qu=1.8 MPa，对应弹性模量取qu的100倍，即180 MPa，TRD 墙体厚度对支护结构承载变形性状影响模拟结果汇总如图3所示。

图3 TRD墙体厚度对支护结构承载变形性状影响模拟结果汇总Fig.3 Summary of the Effect of the Thickness of the TRD Wall on the Deformation Behavior of the Supporting Structure

3.1.2 TRD 墙体水泥土抗压强度对支护结构体系承载变形性状影响

在Midas∕GTS有限元模型中，分别设置TRD墙体水泥土无侧限抗压强度为qu=0.8 MPa、1.8 MPa和2.4 MPa，对应的弹性模量取qu的200倍，即分别为160 MPa、360 MPa和480 MPa，TRD 墙体水泥土刚度（弹性模量）对支护结构承载变形性状影响模拟结果如图4所示。

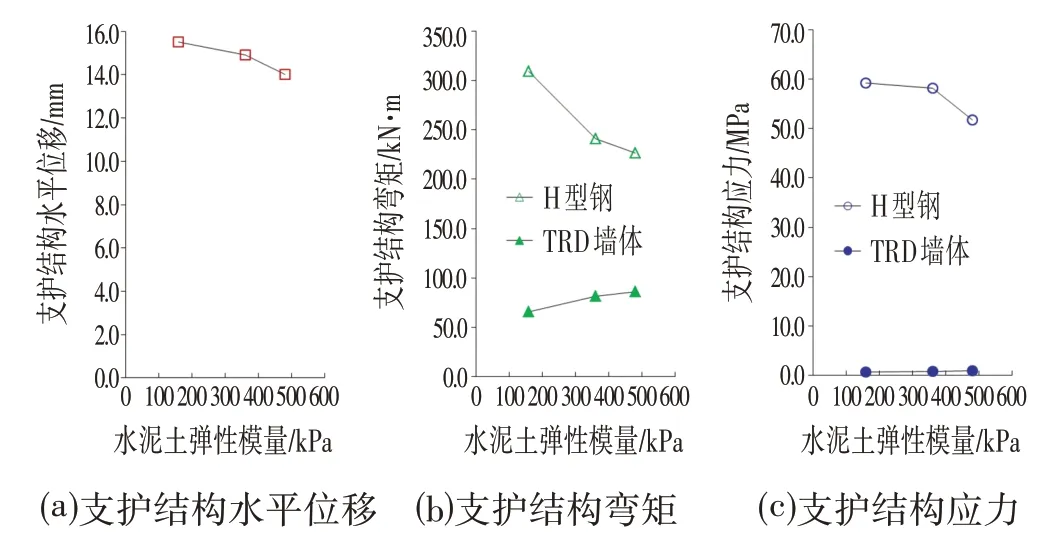
图4 TRD墙体水泥土弹性模量对支护结构承载变形性状影响模拟结果汇总Fig.4 Summary of Simulation Results of the Effect of TRD Wall Cement-soil Elastic Modulus on Supporting Deformation Behavior of Supporting Structure

3.1.3 内插H 型钢水平间距对支护结构体系承载变形性状影响

Midas∕GTS有限元模型中，分别设置TRD墙体厚度为0.85 m，TRD 墙体的水泥土应弹性模量为180 MPa，内插型钢水平间距分别为0.5 m、1.0 m、1.5 m和2.0 m，内插H 型钢水平间距对支护结构承载变形性状影响模拟结果汇总如图5所示。

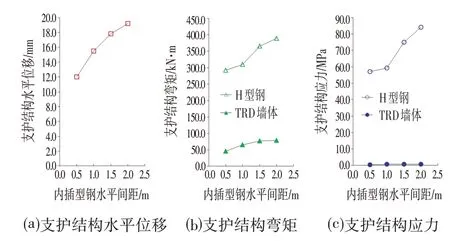
图5 内插H型钢水平间距对支护结构承载变形性状影响模拟结果汇总Fig.5 Summary of the Simulation Results of the Effect of Interpolating the Horizontal Spacing of H-shaped Steel on the Load-bearing Deformation of the Supporting Structure

3.1.4 内插型钢插入深度对支护结构体系承载变形性状影响

Midas∕GTS有限元模型中，分别设置TRD墙体厚度为0.85 m，TRD 墙体的水泥土应弹性模量为180 MPa，内插型钢水平间距为1.0 m，内插型钢插入坑底深度分别为TRD 墙体深度H 的60%、75%、85%和95%，内插H 型钢插入深度对支护结构承载变形性状影响模拟结果汇总如图6所示，其中H为TRD墙体深度。

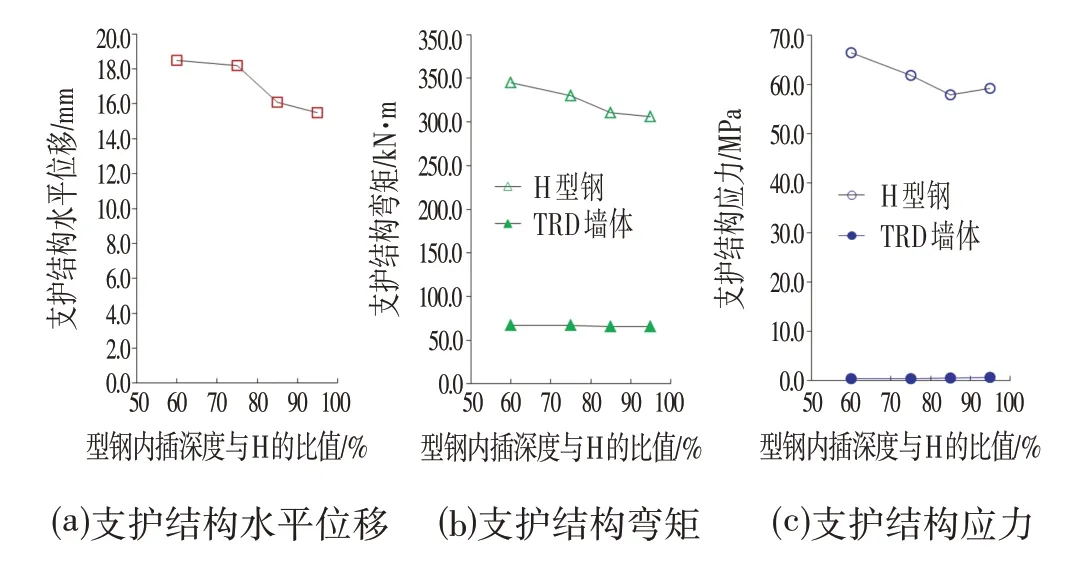
图6 内插H型钢插入深度对支护结构承载变形性状影响模拟结果汇总Fig.6 Summary of the Simulation Results of the Influence of the Insertion Depth of H-beam on the Bearing Deformation of the Supporting Structure

3.2 结果分析

随着TRD墙体厚度和强度的增加，TRD墙体分担的弯矩明显增加，但对支护结构的位移以及TRD墙体分担的应力无明显影响，由TRD墙体和型钢的力学性能可知，TRD 墙体不宜分担较大的弯矩，故建议TRD墙体厚度不宜超过0.85 m。同时，TRD 的墙体厚度并非由支护体系的位移和应力控制，而是由对内插型钢的约束和防止型钢对水泥土的压坏以及TRD 墙体抗渗性控制，因此TRD墙体水泥土的无侧限抗压强度也无必要过高，一般大于1.0 MPa即可。

由图5可知，随着内插型钢水平间距的增加，支护结构的水平位移迅速增加，但对型钢的弯矩和应力分担无明显影响，故调整内插型钢的水平间距能有效地控制支护结构的水平位移。由图6 可知，随着内插型钢插入深度的减小，支护结构的水平位移逐渐增加，型钢分担的弯矩和应力也相应增加，当内插型钢的插入深度小于TRD墙体深度的85%时，支护结构体系的水平位移迅速增加，因此，建议内插型钢的插入深度不宜小于TRD 墙体厚度的85%。型钢分担总弯矩和总应力的比例与各变量因素之间的关系如图7 所示，可知，型钢是分担支护结构体系弯矩和应力的主要构件，随着TRD 墙体的墙体厚度和弹性模量的增加，型钢分担的弯矩逐渐减小，但型钢分担的弯矩仍占75%以上；当内插型钢水平间距小于1.0 m 时，型钢分担弯矩的比例随型钢水平间距的增加而减小，但当内插型钢水平间距大于1.0 m 时，型钢分担弯矩的比例不再随型钢水平间距的增加而变化；内插型钢的插入深度对型钢的弯矩和应力分担无明显影响。不同模拟条件下，型钢分担的应力比例均大于95%。

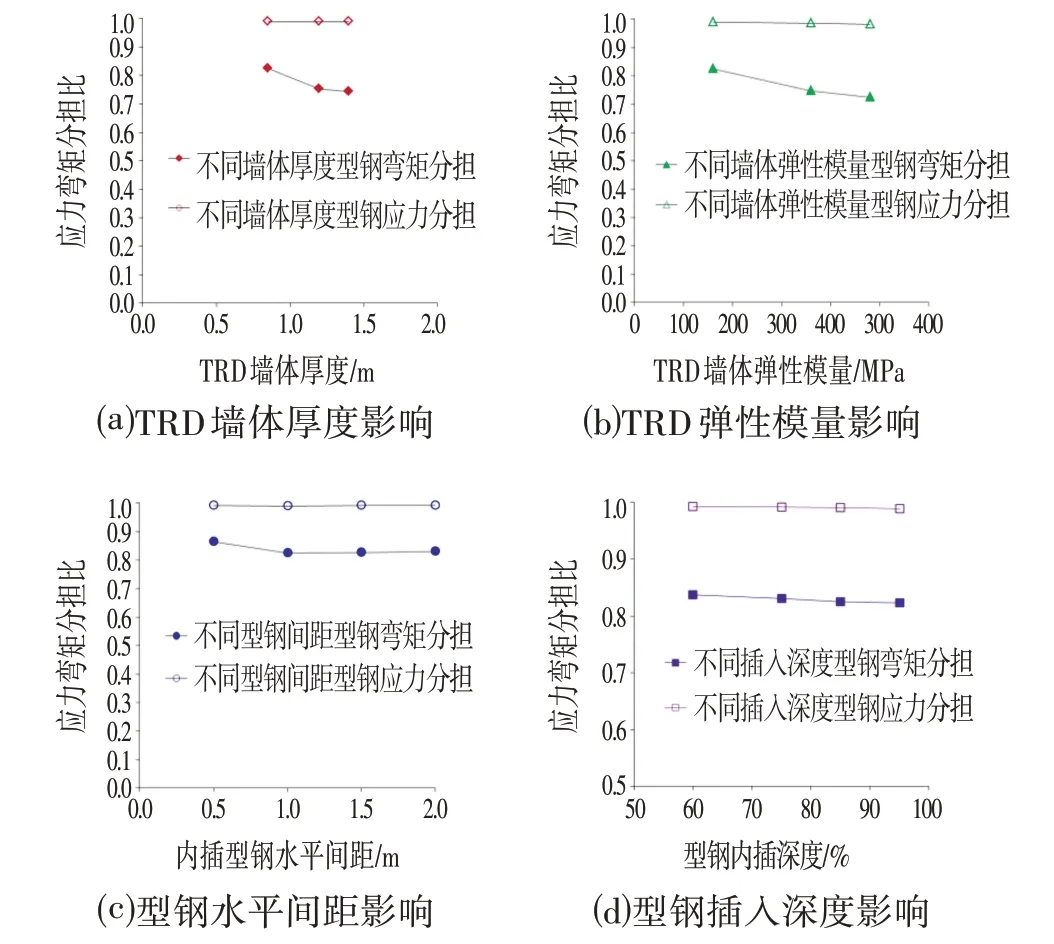
图7 型钢分担总弯矩和总应力的比例与各变量因素之间的关系Fig.7 The Relationship between the Proportion of the Total Bending Moment and Total Stress Shared by the Section Steel and Various Variable Factors

4 数值模拟结果与现场监测结果比较

广州地铁某停车场U 型槽基坑工程TRD 工法支护体系进行了型钢应力和墙体深层位移等项目的监测，基坑设计理正计算结果、Midas∕GTS 计算结果与监测结果对比如图8所示。

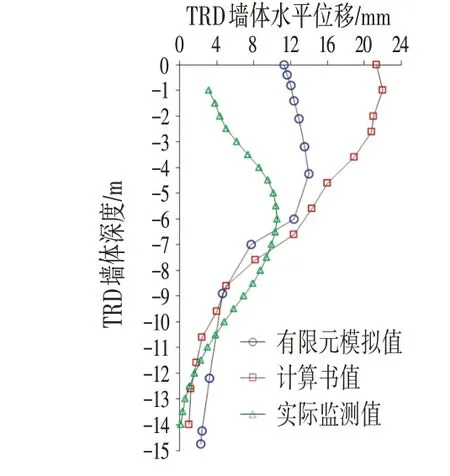
图8 计算结果与监测结果对比Fig.8 Comparison of Calculation Results and Monitoring Results

由图8 可知，TRD 墙体的实测水平位移比理正计算结果和有限元模拟结果均小很多。对于理正计算结果，理正计算时是不考虑TRD墙体抗弯刚度的影响的，但由图9 可知，当TRD 墙体的弹性模量（与抗压强度相关）较大时，TRD 墙体的抗弯刚度可达支护体系的25%，此时，若忽略TRD 墙体对抗弯刚度的影响，设计上是保守的。由现场TRD 墙体水泥土抽芯试验结果可知，TRD 墙体的水泥土130 d 无侧限抗压强度大部分可达4.0 MPa 以上，二者均比有限元中设定的1.8 MPa 大，因此，TRD 墙体本身抗弯刚度实际工程中也会有较大发挥，而TRD 内插H 型钢支护体系的实际位移比理正计算结果和有限元模拟结果小。

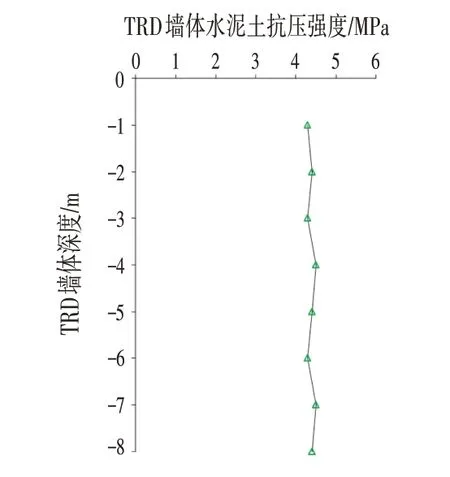
图9 TRD墙体水泥土抗压强度Fig.9 Cement Soil Compressive Strength of TRD Wall

5 结论

广州地铁某停车场U 型槽基坑工程是广州地区首个采用TRD 工法的基坑工程，工程场地地层复杂，对基坑的挡土结构和止水帷幕的可靠性提出了极高的要求，基坑工程采用的内插H 型钢TRD 等厚度水泥土搅拌地下连续墙作为挡土止水结构，确保了基坑工程的顺利实施并有效地保护了周边环境，得到的主要结论如下：

⑴从承载性能方面来看，TRD 工法在广州地区复杂地层中的应用是可行的。

⑵TRD 内插型钢支护结构的位移随型钢水平间距的增加和插入深度的减小而增加，随TRD墙体弹性模量的减小而增加。当型钢插入深度小于TRD 墙体深度的85%时，支护结构体系的水平位移迅速增加。

⑶ 型钢是分担弯矩和应力的主要构件，随着TRD 墙体弹性模量的增加，型钢分担的弯矩逐渐减小，但型钢分担的弯矩仍是主导的；型钢分担的应力逐渐减小，但型钢分担的应力仍占95%以上。

⑷TRD 的墙体厚度并非由支护体系的位移和应力控制，而是由对内插型钢的约束和防止型钢对水泥土的压坏以及TRD墙体抗渗性控制。

⑸ 当现场TRD 墙体水泥土的抗压强度大于1.8 MPa 时，可适当考虑TRD 墙体的抗弯刚度对支护体系整体抗弯刚度的贡献。