高聚物玻璃化转变温度测定不确定度的评估

崔峰波，崔丽荣，章建忠，冉文华，张萍，袁向静

（巨石集团有限公司，桐乡 314500）

0 前言

玻璃化转变是大多数高分子聚合物材料，尤其是非晶态高聚物的固有性质，所以玻璃化转变温度是高聚物的一个重要物理量，高聚物从玻璃态转变为高弹态称为玻璃化转变温度（Tg）［1］,聚合物在玻璃化转变温度时，不仅形变和模量等力学性质发生显著变化，其他的性质比如体积、膨胀系数、比热、导热系数及介电常数也会发生很大变化［2］。

现阶段测试玻璃化转变温度的方法有［3］：差式扫描量热法（DSC）、差示分析法（DTA）、动态热机械分析法（DMA）等。而在这些测试方法中，最常用的是差式量热扫描仪（DSC法）。DSC法测试的原理是当温度升高，高分子聚合物在玻璃化转变温度时，根据热容显著变化的开始点和终止点，然后计算对应的中值，中值对应的温度就是玻璃化转变温度［4］。

玻璃化转变温度是高聚物链运动形式的宏观表现，它决定了材料的工艺性能和使用性能，因此，玻璃化转变温度对聚合物材料的研究有着相当重要的意义［5］。为保障检测结果的稳定、客观，特尝试进行差式量热扫描法（DSC）测试高聚物玻璃化转变温度的不确定度评估。

1 实验准备

1.1 原料

铟：GBW€130182，中国计量科学研究院；

样品A：聚酯类，巨石集团一分厂。

1.2 仪器和设备

差示量热扫描仪：Discovery 2500，美国TA；

坩埚压片机：123，美国TA；

固体铝坩埚：直径2 mm，高度2 mm，美国TA；

电子天平：BP211D，d=0.1 mg，北京赛多利斯。

1.3 测定依据及方法

本次实验依据国际标准《塑料-差示扫描量热法（DSC）-第2部分：玻璃化转变温度和高度的确定》测定。

本次实验的方法为：升温速率为5 ℃/min，升温一次，升温范围为-40~60 ℃；标注方法为拐点法。

2 不确定度来源分析

（1）DSC测量仪器引入的不确定度μ，主要是测量仪器本身的温度重复性μ1、校正用的标准物质的定值μ2、环境温度μ3等引起的不确定度［6］。

（2）样品的不同批次引起的不确定度。

（3）同批次样品，随机采样引起的不确定度。

（4）玻璃化转变温度分析引入的不确定度。

3 不确定度各分量的评定

3.1 DSC测量仪器引入的不确定度

3.1.1 仪器测量的温度重复性引入的不确定度

主要来自仪器测量时温度的重复性，根据标准《测量不确定度和表示》，此项为A类不确定分量。本次以标准物质铟为例进行分析。现将标准物质铟熔融温度10次测量结果分别列入表1。应用贝塞尔公式计算标准物质铟单次测量的标准偏差为：

表1 标准物质铟的熔融温度 ℃

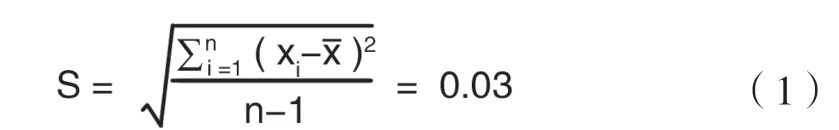
式中：

s——单次测量的标准偏差，无量纲。

n——测量次数。

xi——第i次测量结果。

仪器测量重复性引入的标准不确定度为μ1-1为0.03。

3.1.2 标准物质的定值引入的不确定度

μ1-1来自标准物质的定值引入的不确定度，根据标准《测量不确定度和表示》，此项为B类不确定分量。查阅标准物质携带的证书，其标准熔融温度为156.60 ℃，包含因子为2，扩展不确定度为 0.03 ℃，因此标准不确定度μ1-1为0.015 ℃。

3.1.3 环境温度引起的不确定度

μ1-2来自环境温度的变化引入的不确定度，根据标准《测量不确定度和表示》，此项为B类不确定度。本次使用的标准物质是铟，其熔融温度在 156 ℃左右，环境温度的变化可以考虑为0，故μ1-2为0。如果标准物质的状态和环境温度有关，需考虑环境温度的影响。

DSC测量仪器引入的合成不确定度

3.2 样品的不同批次引起的不确定度

高分子聚合物的结构具有多分散性、不均一的特点［7］，不同的工艺，其玻璃化转变温度是不同的，故针对不同的工艺，玻璃化转变温度的不确定度没有分析的必要。那么针对同一种工艺，不同批次的样品，考虑工艺控制的波动性，其玻璃化转变温度势必也是存在波动的。本次针对同一种工艺，讨论样品的不同批次引起的不确定度，根据标准《测量不确定度和表示》，此项为A类不确定度。取样品A的10个批次，每个批次分别按1.3所述的方法测试玻璃化转变温度，具体数值见下表2。应用贝塞尔公式计算样品A单次测量的标准偏差为：

表2 样品A不同批次的玻璃化转变温度 ℃

式中：

s——单次测量的标准偏差，无量纲。

n——测量次数。

xi——第i次测量结果。

所以样品的不同批次引入的标准不确定度μ2为0.76。

3.3 同批次样品，随机采样引起的不确定度

根据标准《化工产品采样总则》，化工样品的采样过程中有系统误差和随机误差。采样系统误差是由于采样方案不完整、采样设备有缺陷、操作者不按规定进行操作以及环境等的影响，均可引起采样的系统误差。我们可以看到，采样的方案、设备、规定操作以及环境这些因素是定向的，那么造成的误差也是可以避免的，所采样系统误差带来的不确定度就可以视为0。而采样的随机误差是不可以避免的，但可以增加采样的个数来缩小这个误差。因此，根据标准《测量不确定度和表示》，采样的随机误差引入的不确定度为μ3-2为A类不确定度。取样品A的某一批次样品，不同位置重复取样10次，分别按1.3所述的方法测试玻璃化转变温度，具体数值见下表3。应用贝塞尔公式计算同一批次样品A的单次测量标准偏差为：

表3 样品A同批次不同位置的玻璃化转变温度 ℃

式中：

s——单次测量的标准偏差，无量纲。

n——测量次数。

xi——第i次测量结果。

那么同一批次样品随机采样引入的标准不确定度μ3-2为0.61。

随机采样引起的合成不确定度：

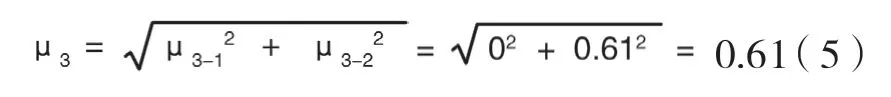
3.4 玻璃化转变温度分析引起的不确定度μ4

依据标准《塑料-差示扫描量热法（DSC）-第2部分：玻璃化转变温度和高度的确定》，测试玻璃化转变温度时必须注明分析方法，分析方法的不同，定会导致玻璃化转变温度的数值各不同。该标准里提及玻璃化转变温度的分析方法有3种，分别是拐点法、半高法及面积法。半高法和拐点法一般分析台阶型转变，使用最常见；面积法是针对台阶伴随吸热峰型的转变分析，其指向性强不常见。但分析时，不管使用何种分析方法，起点和终点的随机选择都会导致玻璃化转变温度稍不同，所以本次讨论的玻璃化转变温度分析引起的不确定度μ4主要是起点和终点的随机选择引起的不确定度，根据标准《测量不确定度和表示》，此项为A类不确定度。取样品A的某一次测试结果，随机选择起点和终点，分别用拐点法和半高2种方法分别分析10个玻璃化转变温度数值，具体见下表4，计算拐点分析法和半高法分析样品A的玻璃化转变温度的测量标准偏差分别为：

表4 两种方法分析样品A的玻璃化转变温度 ℃

式中：

s——单次测量的标准偏差，无量纲。

n——测量次数。

xi——第i次测量结果。

所以2种方法分析下，其标准偏差相差不大，故分析玻璃化转变温度引入的标准不确定度μ4可以预估为0.30。

4 合成不确定度μ4

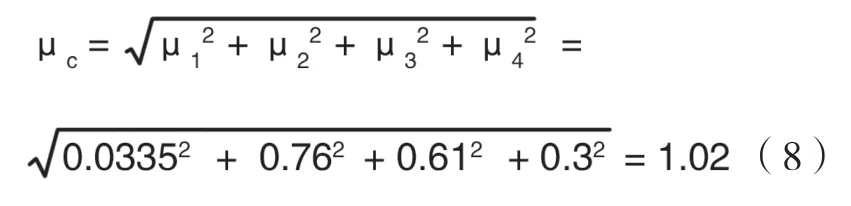
5 扩展不确定度

根据标准《测量不确定度和表示》，不知道或不需要知道自由度和有关合成分布的信息及被测量值得估计区间的置信水平，取包含因子k=2。那么，U=k×μc=2×1.02=2.04。

6 结果报告

该样品A的玻璃化转变温度测定结果报告为：升温速率为5℃/min，升温一次，升温范围为 -40~60 ℃。标注方法为拐点法，以某批次测试结果表示：Tg=（12.02±2.04）℃，k=2。

7 结语

（1）在高聚物玻璃化转变温度的测定过程中，不确定度的来源主要有仪器测量、样品的不同批次、随机采样及玻璃化转变温度分析4个方面。

（2）样品的不同批次和随机采样引起的不确定度对测定的不确定度贡献最大，其次是分析引入的不确定度，测量仪器本身引起的不确定度贡献最小。

（3）高聚物的玻璃化转变温度测试时，必须考虑样品自身的特点引起的不确定性，也就是说在样品自身特点影响下，其批次间的不确定度可大可小。另外，玻璃化转变温度的分析方法也会引起不确定度，所以测试时必须标注分析时使用的标注方法。

（4）仪器引入的不确定度最小，可以通过定期对仪器进行校正，以降低仪器引入的不确定度。确保检测结果的准确性和表达的科学性。