基于联邦滤波算法的无人机集群分层协同导航

谷旭平, 唐大全

(海军航空大学航空作战勤务学院, 山东 烟台 264001)

0 引 言

随着无人机控制和导航技术的不断精进,无人机在军事行动、应急救灾、智能农业、环境监测、灾难响应、地形勘测、商业运输、安全监控等军民领域有着广阔的应用前景。由于单无人机的任务性能和抗毁伤能力有限,研究重心逐渐向无人机集群过渡。无人机集群具有生存率高、成本低、效率高等优点。

无人机导航是关于如何规划无人机安全、快速到达目标任务的过程。无人机必须掌握其位置、速度、航向、出发点以及目标位置。目前主流的导航方法为惯性导航、卫星导航、视觉导航,但都各有不足。因此,提高集群导航精度,必须采取合适的无人机导航。

为了弥补各个导航系统的缺陷,提高导航精度,多采用相对导航技术。文献[20]提出一种适用于编队飞行的基于惯性导航系统(inertial navigation system,INS)和全球卫星导航系统(global positioning system,GPS)的相对导航系统。文献[21]提出一种基于GPS/INS/无线电测距的无人机相对导航。文献[22]采用基于联合滤波器的多源容错组合导航系统。该系统不仅弥补了单一导航系统的不足,而且具有很强的容错能力,可以在出现故障时及时隔离故障系统,使整个导航系统仍能提供可靠精准的导航信息。文献[23]采用的无人机相对导航系统由载波相位差分GPS,INS和超宽带技术组成。该系统可以在GPS受到挑战时,仍能提供精准的导航信息。文献[24]采用基于超宽带辅助的无人机编队相对导航方式。该方案可以在单依靠GPS的情况下,达到比较精准的相对导航效果。文献[25]提出一种通过主从式编队飞行结构的可视化算法来解决主从式飞机的姿态估计和跟踪问题的方法。文献[26]提出一种在GPS受限的条件下基于超宽带信息的间接协同定位技术。文献[27]描述了一种适用于主从结构的无人机编队控制方法,并设计了一个级联回路调整主从无人机之间的相对距离和角度,以提高协同导航的稳定性。文献[28]提出一种在主从式编队模式下,基于双目视觉传感器感知无人机相对方位的方法。

传统的相对导航技术,在导航信息受到干扰时,导航精度容易发散。并且传统单主从式导航结构,在长机发生故障时,导航性能会受到严重冲击。为了解决上述问题,本文建立一种分层协同导航模型,并基于联邦滤波(federated filter,FF)算法,提出了分层协同导航算法,提高集群导航的可靠性。

分层协同导航的优点之一是灵活性,但增加连接性并不会增加集群中所有成员的导航性能,比如导航精度较高的无人机融合导航精度较低的无人机导航信息,会导致导航精度下降。因此,基于图论的全连通融合导航算法,具有较大通信和计算负担,不适用于高动态变化的无人机集群导航,而分层协同导航解决了这一难题。

分层协同导航根据集群中无人机导航精度,将其分为长机层和僚机层,通过长机选择策略,僚机可通过机载数据链融合长机的相对导航信息,提高集群导航信息的利用率,进而提高集群整体的导航性能。同时，利用长机选择策略,减少了精度较低以及非视距误差的测量,减少通信和计算负担。通过仿真,比较分层协同导航算法与传统的单主从式协同导航算法在导航精度,抗干扰能力方面的优劣,进一步验证分层协同导航算法在未来大规模无人机集群导航方面的优势,通过不同算法的仿真比较,进一步验证了FF算法的合理性。

1 分层协同导航系统设计

1.1 分层协同导航结构

传统的单主从式协同导航结构,僚机与长机的协同关系是固定的,僚机利用传感器从长机获取相对导航信息。当长机故障时,系统的可靠性会受到影响。因此，单主从式导航结构不能满足大规模集群导航条件。为增强无人机集群导航的可靠性,设计如图1所示的分层协同导航。

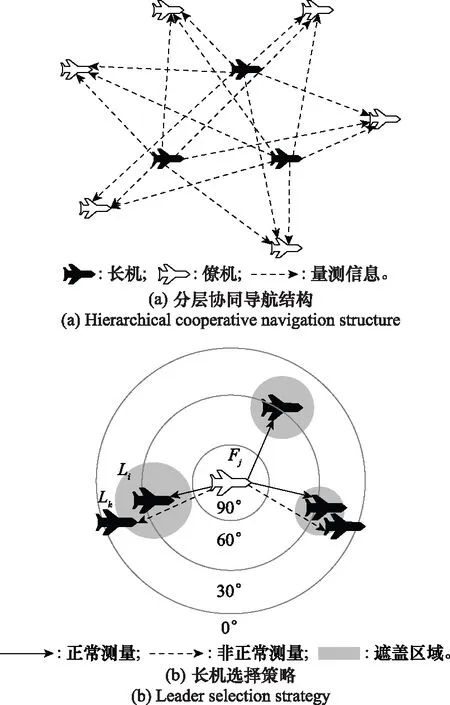
图1 分层协同导航Fig.1 Hierarchical cooperative navigation

如图1(a)所示的分层协同导航架构,摆脱了以往单主从模式固定的长僚机搭配。根据导航精度将无人机集群分为长机层和僚机层,僚机可以获得长机层的相对导航信息。如果某一架长机故障,其他长机正常,僚机仍可以获得其他长机的协同导航信息,因此该分层协同导航结构具有较好的可靠性和鲁棒性。如果给出至少一架长机的相对导航信息,就可以确定僚机的位置。这意味着,该协同导航结构具有灵活性的特点,即只需要一架长机,就可以进行协同定位,这对于长僚机之间通信部分出现故障的情况,具有良好的鲁棒性。该分层协同导航结构中,一架僚机可以获得多架长机的协同导航信息,与传统的单主从式协同导航结构相比,该结构更能保证故障条件下僚机的导航性能,并且在大规模无人机集群条件下,更能充分利用多机协同测量信息,提高集群导航信息的利用率。

如图1(b)所示的长机选择策略考虑到长机之间的相互遮掩,避免了测量信号的相互干扰。根据导航系统提示,可以掌握僚机与其他长机之间的方位信息,对导航误差引起的方向不确定性进行估计。以某一僚机为中心,估算其他长机在球坐标系的遮掩区域大小,对可以进行长僚机测量的长机进行区分,建立长机选择策略优先级,减少非视距误差对导航性能的影响。如图1(b)所示,根据长僚机之间的方位信息,僚机可以获得5架长机的协同导航信息;但当考虑长机遮掩区域的影响时,僚机只能获得3架长机的协同导航信息。

1.2 协同导航系统设计方案

图2为无人机集群协同导航系统设计方案,集群中每一架UAV都搭载一定精度的INS。僚机搭载激光测距测角设备和多普勒测速仪等相对导航设备,用于测量长僚机之间的相对方位、相对距离和相对速度。僚机融合处理自身导航设备以及机载数据链提供的长机层的导航信息,建立测量模型,并通过滤波估计INS误差,实现导航信息的校正。通过融合长机层的导航信息,提高集群导航信息的利用率,进而提高集群整体的导航性能。

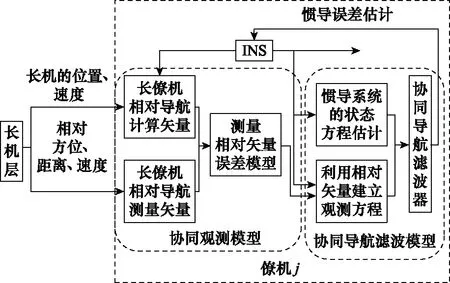
图2 分层协同导航系统总体方案Fig.2 Overall scheme of hierarchical cooperative navigation system

2 相对导航矢量模型设计

2.1 相对导航矢量测量模型

僚机测距与测速传感器测得第架长机与第架僚机的相对速度与距离为

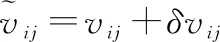
(1)

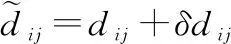
(2)

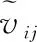
僚机激光测角传感器测得第架长机与第架僚机的相对角度为

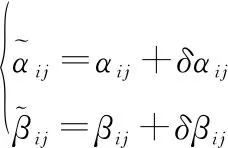
(3)

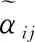
分别为相应角度测量误差。

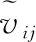
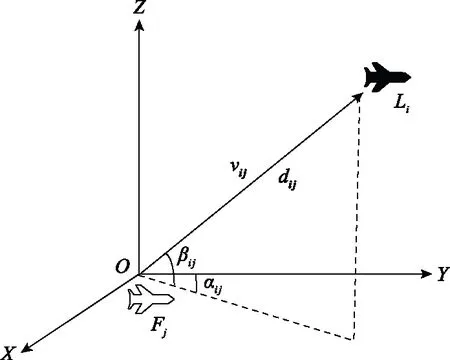
图3 僚机相对导航测量Fig.3 Follower relative navigation measurement

(4)

将式(1)和式(3)分别代入式(4)得到:

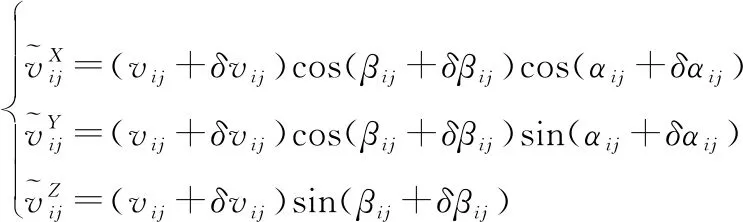
(5)

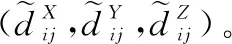
由于,,都很小,因此得到相对速度测量误差模型:

(6)

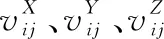
载体坐标系到导航坐标系的变换矩阵为

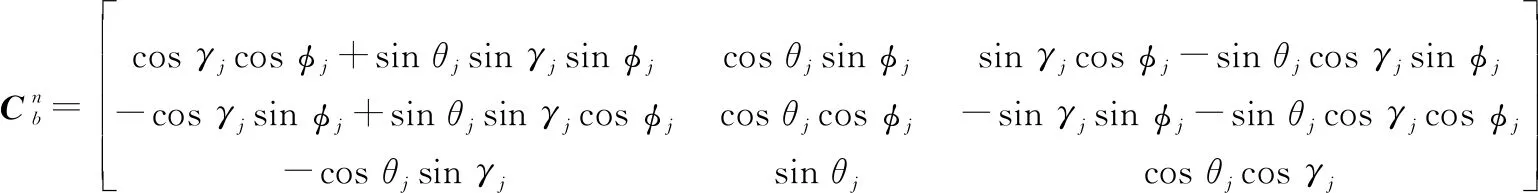
(7)

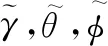
(8)

则根据式(6)和式(7)可以得到相对导航速度在导航坐标系的分量为

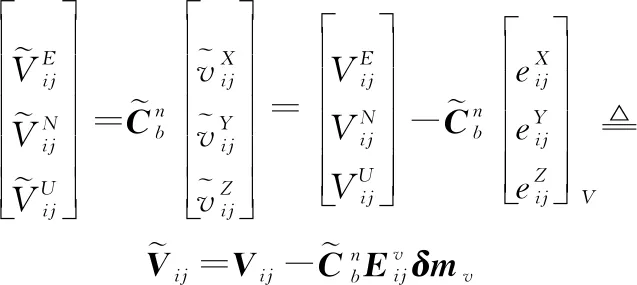
(9)

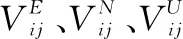
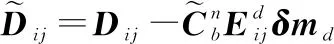
(10)

2.2 相对导航矢量计算模型

221 相对速度计算模型

长机与僚机导航系统解算的速度为

(11)

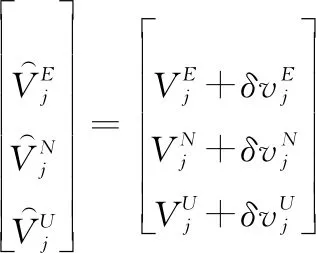
(12)

长机与僚机导航系统解算速度相减得到两机相对速度计算值:

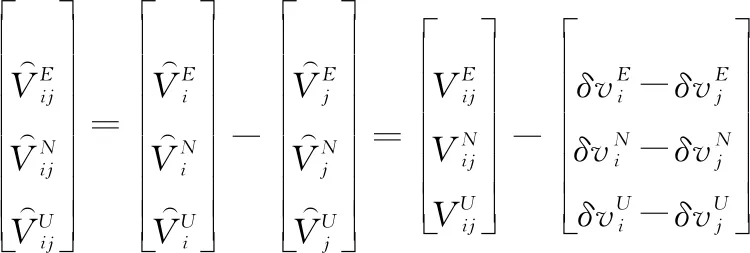
(13)

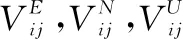
222 相对距离计算模型

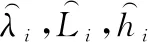
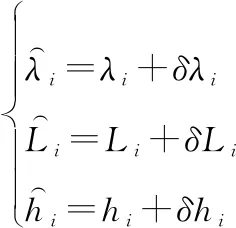
(14)

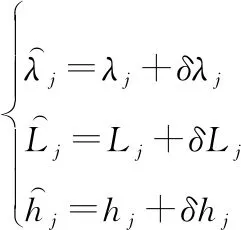
(15)

式中:,,和,,分别为长机与僚机的经度、纬度和高度真实值；,,和,,分别为相应误差。

依据式(14)和式(15)解算出长机与僚机的位置在地球坐标系的分量为

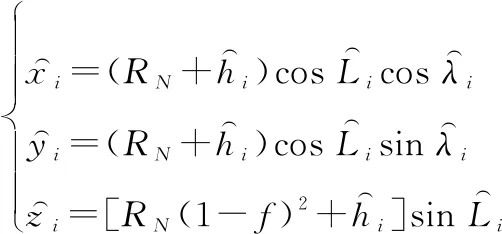
(16)

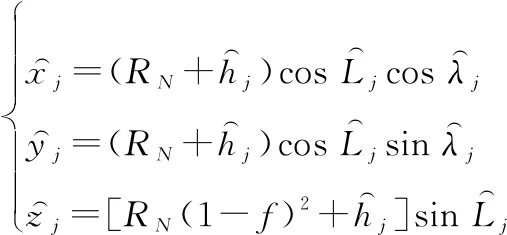
(17)

式中:为地球卯酉圈半径；为椭圆度。

由于,,都很小,因此得到长机的位置误差模型为

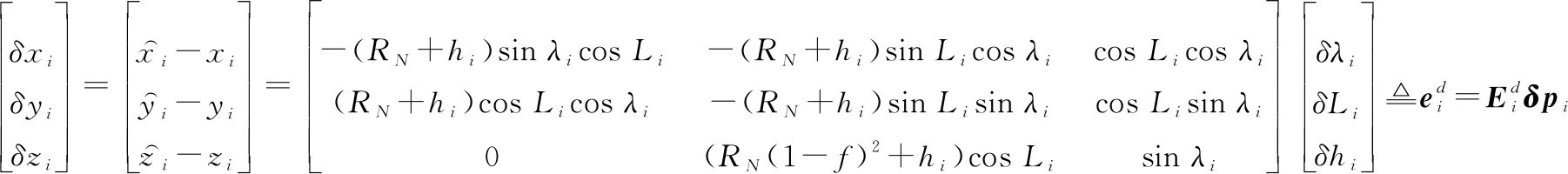
(18)

同理得到僚机的位置误差模型为

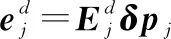
(19)

地球坐标系到导航坐标系的转换矩阵为

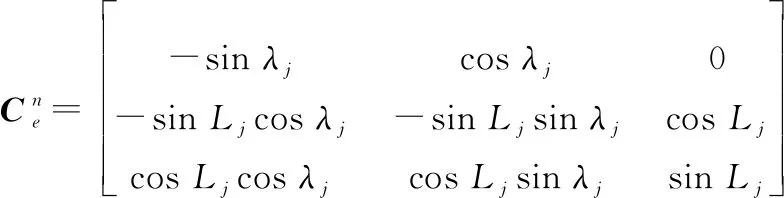
(20)

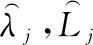
(21)

则长机与僚机的相对距离计算值在导航坐标系下的分量为

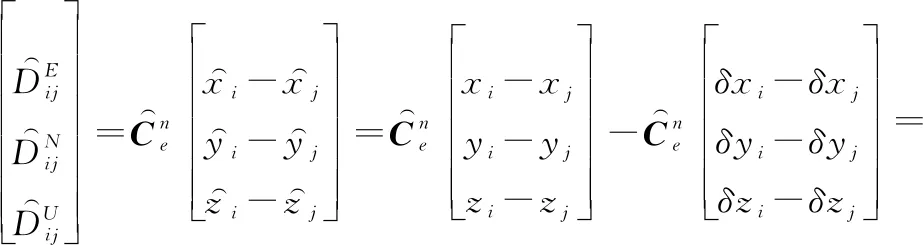
(22)

3 分层协同导航模型

3.1 系统的状态方程

选择僚机的INS误差模型作为状态方程:

()=(,-1)(-1)+(,-1)(-1)

(23)

式中:为INS误差的状态转移矩阵;为INS的噪声输入矩阵;为INS的噪声矢量,其误差协方差为;为INS的误差矢量,定义为

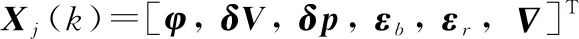
(24)

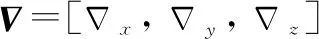
3.2 导航系统观测方程

式(9)和式(13)相减得

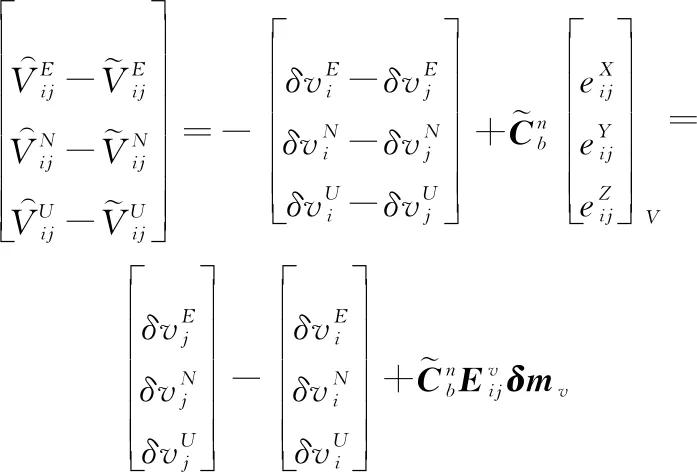
(25)

则相对速度测量方程为

(26)

式(10)和式(22)相减得

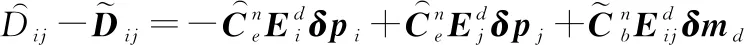
(27)

则相对距离测量方程为

(28)

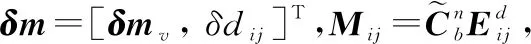
由式(26)和式(28)联立得到观测方程为

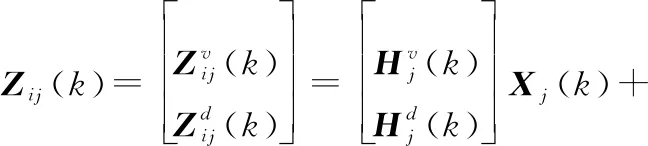
(29)

则量测噪声的误差协方差矩阵为

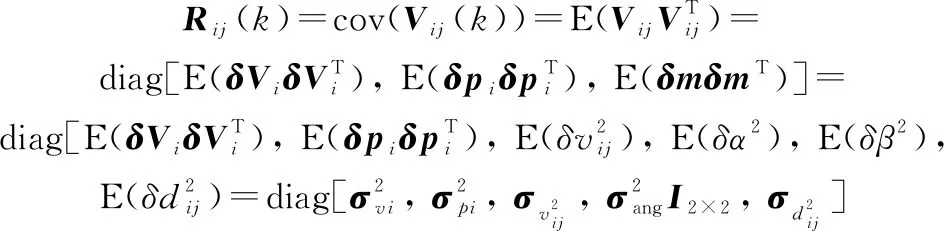
(30)

式中: 和分别为长机提供的速度与位置协方差;和分别为相对速度与距离传感器的噪声协方差；为相对角度传感器的噪声协方差,并且对于僚机,相应的相互独立。

为了方便描述,令

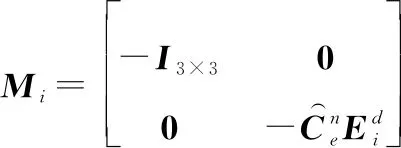
(31)

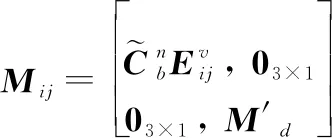
(32)

=[,]

(33)

假设无人机集群中有架长机,则僚机的观测方程为

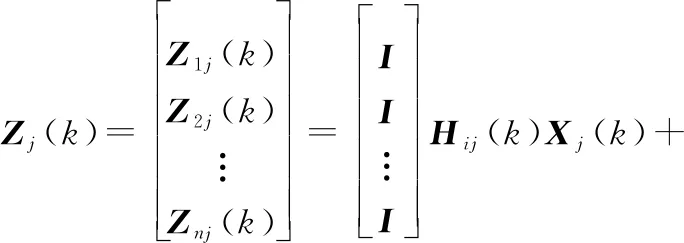
(34)

则僚机的误差协方差矩阵为

(35)

4 分层协同导航算法

4.1 FF算法

面对未来大规模无人机集群任务,若采用集中式的信息融合,计算和通信负担重,并且容错性差。而FF算法作为一种新型的分散化滤波方法,降低了算法的复杂性,提高了算法的容错性与可靠性,而且FF算法易于实现,信息分配方式灵活,计算量小。

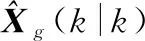
图4 FF结构框架Fig.4 Structure framework of FF

FF器的工作流程分为4个步骤。

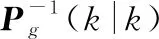
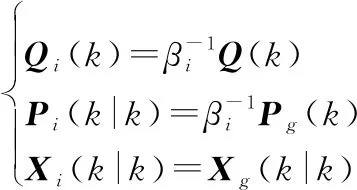
(36)

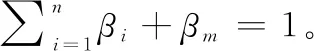
时间更新。子滤波器与主滤波器的时间更新相互独立,其中=1,2,…,,,则时间更新方程为

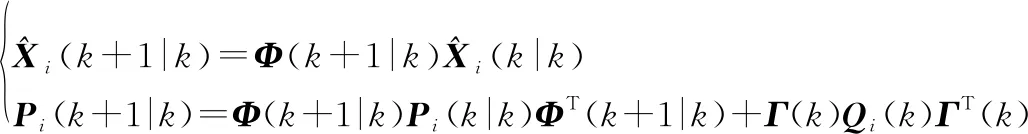
(37)

量测更新。量测更新只在子滤波器中进行,即=1,2,…,,则量测更新方程为

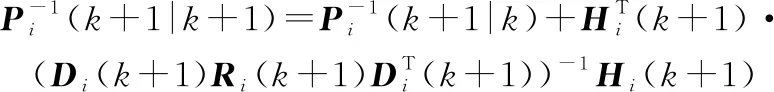
(38)

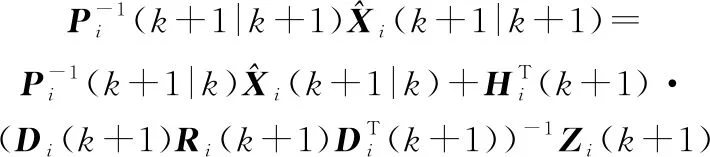
(39)

信息融合。将各个局部滤波器的局部估计值进行融合,得到全局最优估计,即

(+1|+1)=

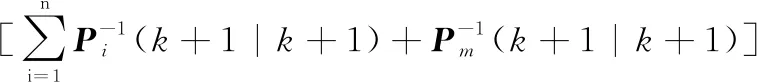
(40)

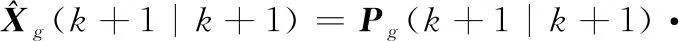
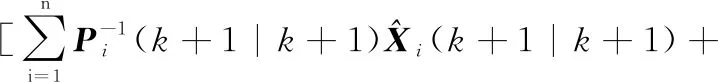
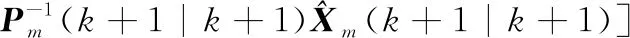
(41)

4.2 分层协同导航算法流程

根据前文所建立的滤波模型,以FF算法为基础,设计了本文的分层协同导航滤波算法,具体步骤如下。

确定无人机集群中长机数量;

依据式(23)、式(36)和式(37)进行信息分配与时间更新;

依据式(9)和式(10)以及测得的测距测速测角信息,获得相对导航测量信息;

根据长僚机导航系统提供的位置速度信息,依据式(13)和式(22)获得相对导航计算信息;

依据式(29)建立协同导航观测模型,其中式(30)代表的误差协方差矩阵()是根据测角误差,测距误差,测速误差以及长机的导航系统的位置误差和速度误差 确定;

根据式(38)～式(41)进行滤波状态的更新,以及局部传感器的信息融合。

5 仿真分析

5.1 仿真设置

为了验证算法的有效性以及协同导航模型的正确性,进行数据仿真。参与本次仿真的无人机共25架,其中长机7架,仿真时间为3 000 s,长机的定位误差为2 m,仿真中INS以及相对导航设备的相关参数如表1所示。如无特别提示,仿真都是在该条件下进行。此外,进行100次蒙特卡罗实验,研究不同导航因素对导航性能的影响。同时对传统的单主从式导航(single leader-follower, SLF)算法和分层协同导航(hierarchical collaborative fusion, HCF)算法进行仿真比较。

表1 导航传感器参数

5.2 相对导航矢量精度分析

对不同测距、测速、测角精度下的无人机集群导航进行仿真,分析相对测距、测速和测角精度对僚机1导航性能的影响,如图5～图7所示。

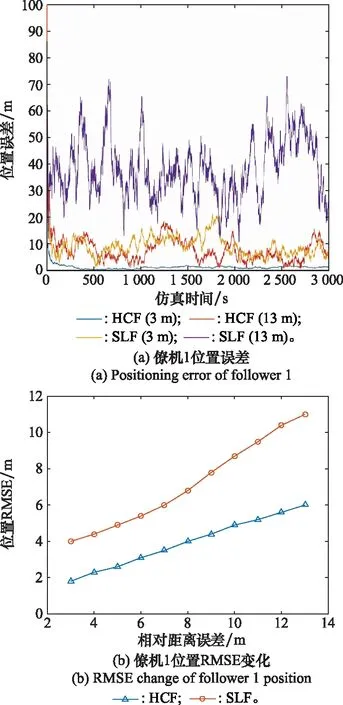
图5 不同测距精度下的位置误差Fig.5 Position error under different ranging accuracies

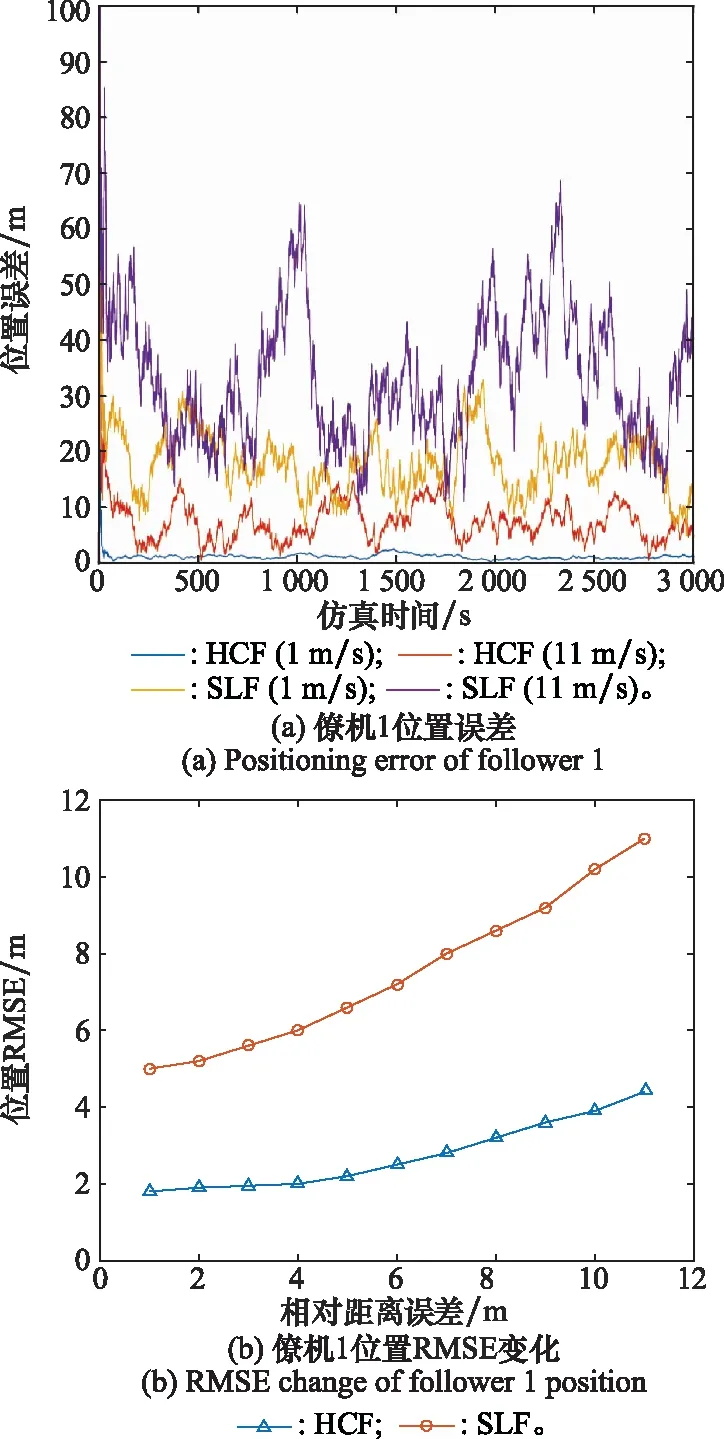
图6 不同测速精度下的位置误差Fig.6 Position error under different velocity accuracies

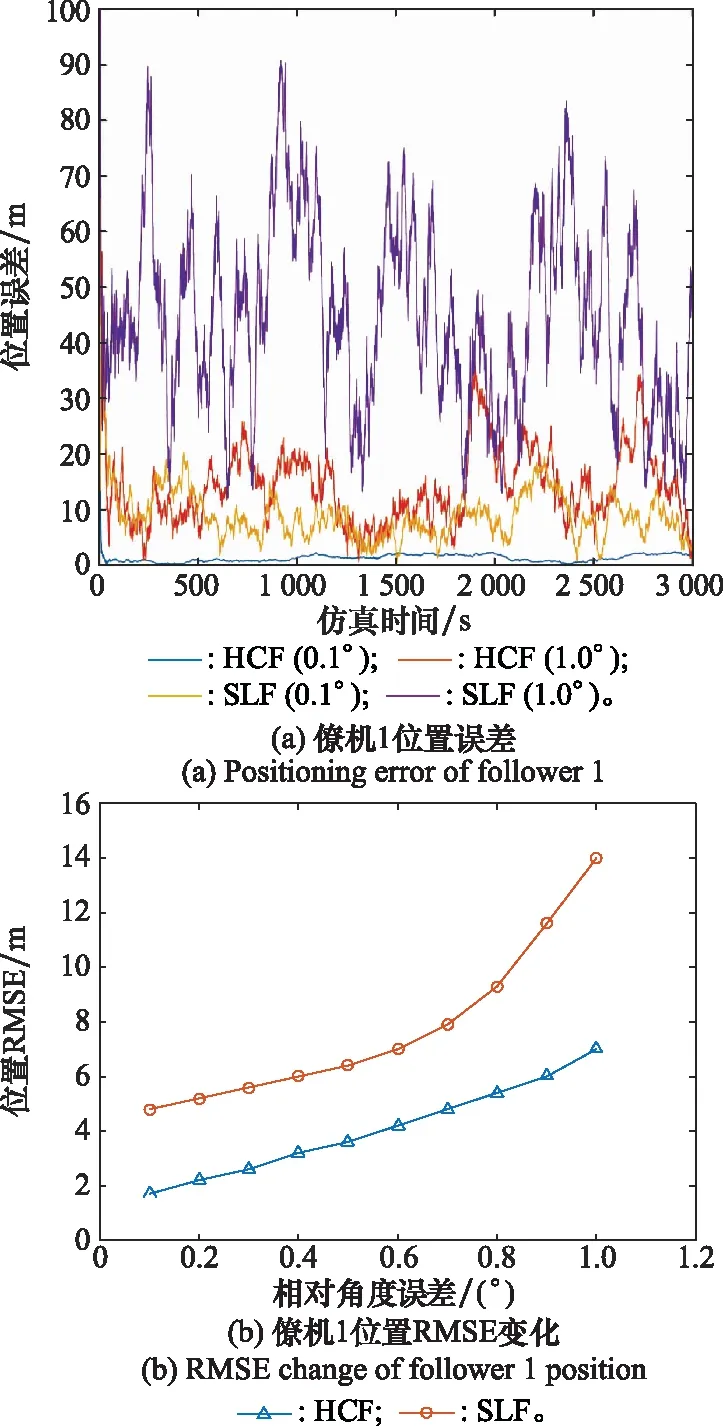
图7 不同测角精度下的位置误差Fig.7 Position error under different angular accuracies

图5(a)、图6(a)和图7(a)分别给出了僚机在3 m和13 m的测距精度,1 m/s和11 m/s的测速精度,1.0°和0.1°测角精度下僚机的定位误差曲线,并对SLF算法与HCF算法进行比较。图5(b)、图6(b)和图7(b)显示了在不同测距、测速和测角精度下的僚机位置均方根误差(root mean square eror, RMSE)。

如图5(a)、图6(a)和图7(a)所示,提高测距、测速和测角精度,可以减小SLF算法与HCF算法的定位误差。在相同的测距、测速和测角精度下,HCF算法的定位误差比SLF算法要小。如图5(b)、图6(b)和图7(b)所示,随着相对导航测量精度的提高,僚机的定位RMSE减小。在相同导航测量精度下,HCF算法比SLF算法的定位精度提高了18%～27%。根据曲线的增长趋势可知,HCF算法受相对导航测量精度的影响较小。从图5(b)、图6(b)和图7(b)可以看出,与SLF算法相比,HCF对导航精度的要求较低,也即为了满足一定的导航性能,HCF算法降低了相对测量精度的要求。

5.3 集群中长机数量对导航性能的影响

图8显示了无人机集群中长机的比例对导航精度的影响。图8(a)显示了长机占比10%和30%的情况下,SLF算法与HCF算法的定位精度误差。图8(b)显示了长机占比为10%～60%时,僚机的定位RMSE变化。

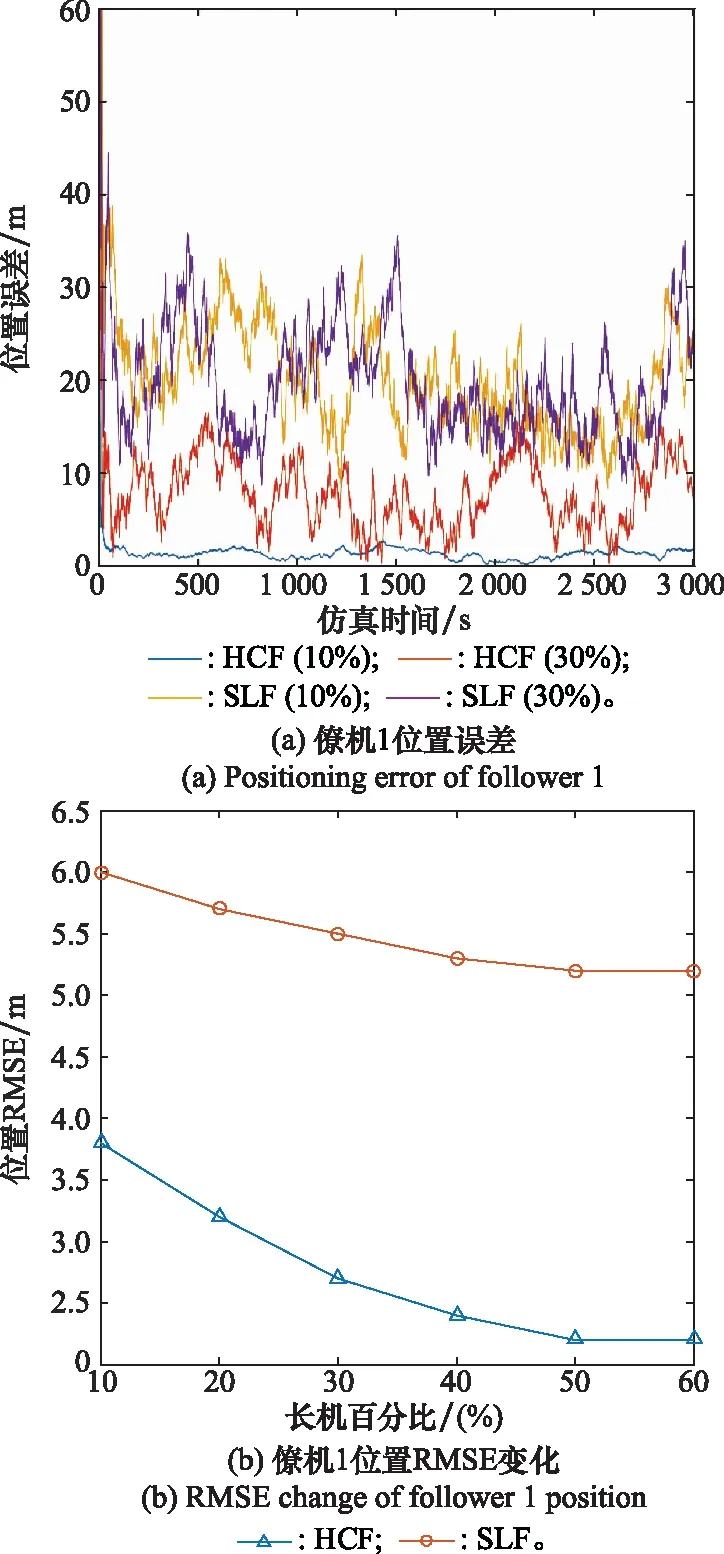
图8 不同长机比例下的位置误差Fig.8 Position error under different proportions of leader

从图8(a)可以看出在,对于HCF算法,提高长机占比可以提高导航精度,但对于SLF算法来说,效果不是很明显。并且在长机占比相同的情况下,HCF算法的定位精度更好。这也说明HCF算法较SLF算法更能充分利用无人机集群中协同导航信息,提高整体的导航性能。从图8(b)可以看出,在长机占比相同的情况下,HCF算法较SLF算法具有更低的定位RMSE。随着长机比例的增加,无人机集群的定位RMSE逐渐降低,但下降趋于平缓,长机占比从10%增加到30%的定位精度的提高要明显大于长机占比从30%到50%的。因此可以看出,提高长机比例可以降低定位误差,但当长机占比达到45%左右时,效果不是很明显,此时再增加长机占比,只会增加导航成本。

5.4 导航性能的稳定性分析

假设给僚机1提供导航信息的长机在1 500～2 000 s内受损,无法提供导航信息。图9(a)显示了僚机1在长机故障情况下的定位误差,图9(b)显示了长机1故障下自身的定位误差,图9(c)显示了在不同数量长机故障时的集群定位RMSE变化。如图9(a)所示,在1 500～2 000 s内,由于给僚机1提供导航信息的长机发生故障,对于HCF算法,僚机1仍能保持定位精度,但是对于SLF算法而言,定位误差迅速发散。如图9(b)所示,对于SLF算法,当长机1故障时,定位误差迅速发散,但对于HCF算法,长机1可以利用无人机集群中其他长机的导航信息实现定位误差校正,保持定位精度的稳定性。如图9(c)所示,随着长机故障数量的增加,集群整体定位RMSE增加。但在相同的长机故障数量下,HCF算法比SLF算法具有更小的定位RMSE,并且在长机故障数较多的情况下尤为明显。从曲线的增长率可以看出,HCF算法较SLF算法受长机故障数影响较小,也就减小了长机故障对集群导航性能的影响。所以HCF算法比SLF算法更能保证导航性能的稳定性。

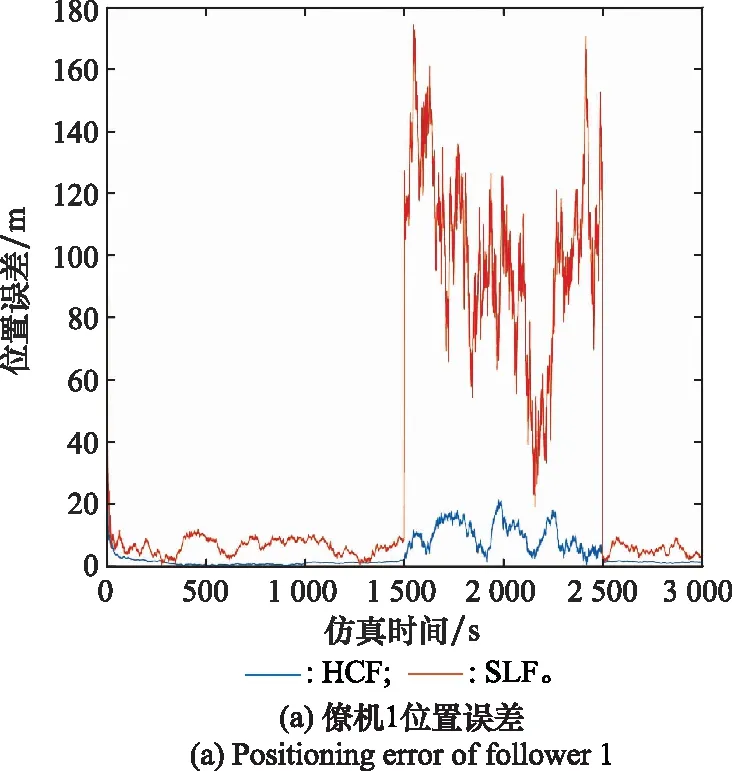
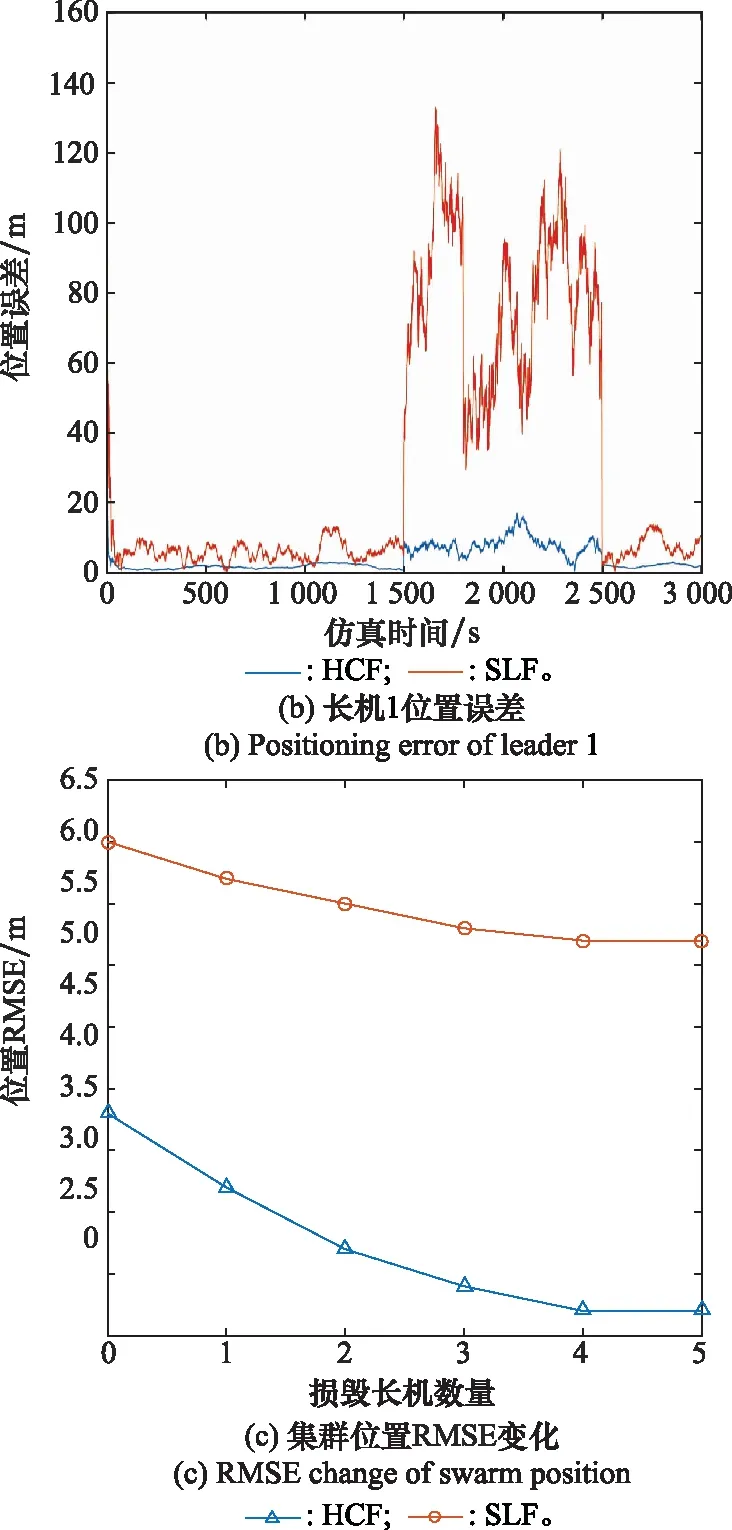
图9 长机故障引起的导航误差Fig.9 Navigation error associated with leader plane failure

5.5 算法性能测试

为验证本文FF算法的性能,选取卡尔曼滤波(Kalman filter,KF)算法与粒子滤波(particle filter,PF)算法进行仿真比较,仿真结果如图10所示,仿真时间如表2所示。

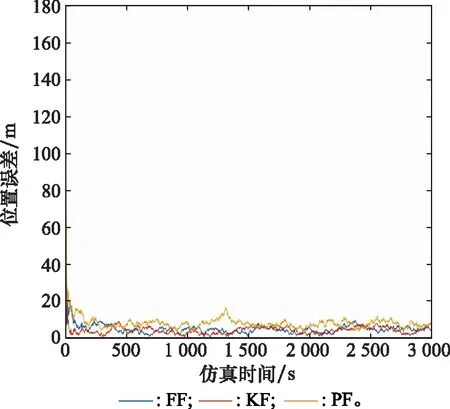
图10 不同滤波算法比较Fig.10 Comparison of different filtering algorithms

表2 不同算法仿真时间对比

在滤波初始条件相同的条件下,有重置的FF算法和集中式融合算法是等价的。从仿真结果看出,在仿真精度上,FF和KF的滤波精度要稍好于PF算法。但是在仿真时间上,由于FF算法的各子滤波器的滤波运算是并行的,这使得运算速度大大提高,运算时间仅为集中式融合算法的二分之一,由仿真结果可以看出无论是在仿真精度还是在运行时间上,FF算法都具有很大优势,进一步验证了FF算法在分层协同导航方面的优势。

6 结 论

为了改善传统单主从式无人机协同导航的性能,提高集群对导航信息的利用率以及集群导航性能的稳定性,本文基于FF算法,提出了一种无人机集群分层协同导航算法,建立了无人机集群分层协同导航模型。仿真结果显示,与传统的SLF算法相比,HCF算法提高了集群导航信息的利用率以及定位精度,并且受相对导航测量精度影响较小,提高了协同导航系统的容错能力以及稳定性,保证了协同导航系统整体的导航性能,通过不同滤波算法的比较,验证了FF算法的合理性。