针对要点防空模型的作战兵力优化研究
蔺向阳, 邢清华, 刘付显
(空军工程大学防空反导学院, 陕西 西安 710051)
0 引 言
在现代化联合作战行动中,军队的防空作战能力对整体作战行动有着重要的意义。红方强大的防空作战能力不仅能通过远程威慑和近程辅助航空兵的方式实现对蓝方的综合打击,削弱蓝方空中作战力量,夺取制空权;更重要是能够对红方指挥所、军械库、后勤库等军事战略要点进行有效保卫,使其免受打击,延长在战争中生存时间,最大程度发挥其作战价值,引导战场平衡向有利于红方胜利的方向推动。
如何根据蓝方的火力配置合理分配红方兵力,使防空能力达到最强,并对其效能准确评估,是至关重要的。近几年,在兵力分配的研究中,赵鹏蛟等人分别使用了排队论、决策论、蚁群算法和模糊决策、Memetic等算法[1-5]。在具体防空作战兵力分配方面,李菱歌等使用了遗传算法[6-8],刘宁使用了动态规划[9],刘立佳等人使用了多目标优化方法[10-11],刘志成和孔祥宇则分别运用了博弈论和图论[12-13]。邢清华等人则运用建模仿真方法进行了研究[14-18]。同时,在作战效能的评估方面,罗宇等人采用改进对数法等多种方法对武器效能进行了评估研究[19-23],周立尧等人对不同军兵种的作战效能进行了评估[24-26]。外军方面,Fauske对军事行动任务规划进行优化[27]。Mika和Womer使用禁忌搜索等算法对人力和资源调度优化问题进行了研究[28, 29]。Erlandsson使用“生存模型”对军队作战能力进行了评估研究[30]。
国内外专家采用不同的方法研究了兵力优化问题与作战效能评估问题,但是绝大多数研究的作战过程都较为单一,难以适用于现阶段实际作战通常具有全领域、多过程作战的特点。本文立足于当前我国周边军事形势,对某近海区域为作战背景进行抽象,建立数学模型。基于要点总毁伤期望最低的作战目标;采用多步建模,层层优化的方法,对近海小规模局部战争中联合防空作战的兵力配置进行研究;提出一种新的对类二项分布的期望求解方法,实现了对不同层级之间剩余作战力量的数量期望的准确求解;最终给出与其相适应的评估方法和指标用以对优化效果定量评估,实现优化与评估相统一,使整个模型更加完备。
1 问题描述
取近海区域小规模联合作战背景,对实际作战情况进行抽象,得到作战示意图如图1所示,红色代表红方作战力量,蓝色代表蓝方作战力量,靶心代表蓝方欲攻击的红方要点目标。
红蓝双方作战目标与作战原则可简化如下。
蓝方:通过导弹远程打击红方要点目标,或通过航空兵突进红方要点上空后投掷弹药进行轰炸。
红方:根据情报所得红蓝双方装备参数,以及蓝方兵力分配,优化红方兵力分配,拦截蓝方攻击,将要点损失降到最小。
红方作战原则:为避免蓝方深入,应使用航空兵与舰船将蓝方航空兵尽可能拦截在海上。对成功突防的蓝方航空兵使用地面防空二次拦截。同时红方地面防空还承担对蓝方远程导弹的反导拦截任务。
根据上述任务,对模型作出合理假设如下。
假设 1假设蓝方航空兵力量以战机编队形式呈现。每组编队成功突防后具备一次轰炸能力。
假设 2假设红方航空兵力量和舰船力量都以编队形式呈现,在海上对蓝方战机编队进行拦截,二者统一定义为海上拦截作战力量,简称海上力量。每组编队具备一次拦截能力。
假设 3假设红方地面防空力量特指地空导弹,简称地导力量。每枚导弹为一个作战单元,具备对蓝方战机编队的一次防空拦截能力,或对蓝方导弹的一次反导拦截能力。
假设 4假设双方作战规则为,在单位时间内,蓝方特定作战单元主攻一个要点,对同一要点攻击的蓝方多个作战单元遵循排队打击原则,即不存在两个打击力量能精确同时到达。红方特定作战单元,只能对蓝方一个目标单元进行一次排队拦截。若目标被友军提前拦截,则更换对同一要点进攻的下一目标进行拦截。
假设 5假设蓝方的总进攻单元数量不多于红方的总拦截单元数量。否则,必然存在蓝方作战单元不受拦截地对红方要点进行直接打击,致使红方防空任务失败。
2 模型建立
2.1 模型分析与基础参数设定
设红方待保护要点数量为NY,对第k个要点,定义其在受到打击后,剩余作战价值与要点完好时总作战价值的比率为耐久价值Vk,要点完好时Vk0=1。定义要点耐久价值为保卫系数Ek对耐久度Dk的加权。其中耐久度为要点未被摧毁部分所占比率,是承受蓝方多次打击造成的毁伤率的总乘积,要点完好时Dk0=1。保卫系数为相对保卫重NHi要度系数E1k、相对保卫难度系数E2k、相对抗毁伤影响系数E3k的总乘积。其中,相对保卫重要度系数与要点战略地位呈正相关;相对保卫难度系数与要点位置纵深、隐蔽性和机动性呈正相关;对抗毁伤影响系数与要点对损伤敏感程度呈负相关。
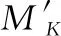
由上可得红方第k个要点经受蓝方第jK种战机编队x次轰炸和第jD种导弹y次打击后,要点耐久度降低为
(1)
要点耐久价值将降低为
Vk=DkEk
(2)
式中:Ek=E1kE2kE3k。则根据作战目标得待优化目标函数为
(3)
即蓝方单位时间的进攻后,红方总体剩余耐久价值最高。
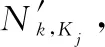
设已知拦截概率为:第i种海上力量对蓝方第j种战机编队拦截概率为PHKij(0≤PHKij≤1);第i种地导对蓝方第j种战机编队拦截概率为PLKij(0≤PLKij≤1);第i种地导对蓝方第j种导弹拦截概率为PLDij(0≤PLDij≤1)。而作战过程中实际拦截概率不仅受制于武器装备的影响,亦受制于包括双方的情报能力,指战员能力,装备运用程度等主观能力影响。将其统一设为双方主观综合能力比w(0.1 P=1-(1-P0)w (4) 式中:P为w修正后实际拦截概率;P0为未考虑w的理论拦截成功概率。 由此,即可针对目标函数式(3)对红方兵力分配进行优化,但由于作战过程分海上拦截和地导拦截两个阶段,无法直接求解,故使用分布建模,逐级优化的思路,将整个问题分为两个子过程逐次建模优化。 2.2.1 海上拦截阶段兵力分配建模 在此阶段,红方海上力量对蓝方战机编队拦截。待优化目标函数为 (5) qij=cijPHKij (6) 对式(6)进行w修正: qij=cij(1-(1-PHKij)w) (7) 故目标函数式(5)可等价于: (8) 综合约束条件,可得完整模型,其中C1,k矩阵为待优化变量。显然此优化为凸规划问题,故目标函数的极值点必然是最值点,即C1,k将具有全局最优解。 2.2.2 地导二次拦截阶段力量分配建模 由此,可得目标函数: (9) (10) 经w修正为 (11) 同理第2.2.1节,目标函数(9)可转化为 (12) 式中:C2,k矩阵为待优化变量。 2.2.3 兵力分配效能评估 由上可预测经过本轮作战结束后,红方第k个要点剩余耐久度: (13) 剩余耐久价值为 Vk=DkEk (14) 以此可作为本次联合防空作战中兵力分配的效能评估指标。 模型建立在对实际作战中重要参数的抽象提取,确保了模型假设的可靠性。 对于一个复杂的多过程作战采取分步建模、层层优化的方法。由于每一层优化都是凸规划,故可以保证各层优化的结果都可取得全局最优解。而结合实际情况与作战经验综合分析确定的红方作战原则,即将蓝方航空兵尽可能拦截在海上,保证了上层优化所得数据对下层有效,即由上至下到最终优化的结果,一定是在当前排队打击的作战规则前提下,整个作战过程兵力优化的全局最优解。 效能评估是通过对概率的计算得出的,不仅可得到优化的量化评估值,且此估值具备直观的现实意义,即红方要点受损程度的期望值。 根据第2.2.1节中模型,根据式(8)的约束条件,结合相关已知参数与式(7),对式(8)进行优化,可得到最优海上力量分配矩阵C1,k。 3.2.1 问题分析 3.2.2 问题求解 图2为假设红方有两种拦截力量,每种5个编队,对蓝方拦截概率分别为0.8和0.6时,蓝方被拦截数量概率分布图,其中横轴为拦截蓝方数量,纵轴为相应的概率分布。图2中,绿色是标准正态分布参考线,其中均值为5×0.8+5×0.6=7,方差为5×0.8×0.2+5×0.6×0.4=2。红色线为蓝方数量无限制时,两个独立的二项分布构成的拦截蓝方数量的概率分布。蓝色线和黑色线分别为蓝方数量限制在6和8时,两个类二项分布构成的拦截敌数量的真实概率分布。不难看出,红线和绿线近似拟合,说明当蓝方数量无限制时,其实际概率分布与正态分布近似。而在6之前,蓝色点都落于红色线上,8点之前,黑色点都落于红色线上,说明在限制之内两个试验独立性不受影响。影响表现在超过上限部分的概率分布,会被统一压缩在上限点处,如蓝色的6和绿色的8处概率激增,之后概率为0。 该期望前项为独立项期望,后项为非独立项期望。 (15) 其中,蓝方导弹期望为 (16) 蓝方战机编队期望为 (17) 上文中,通过公式推导与理论叙述说明了算法必然取得全局最优,本节通过一个想定战例对上述模型及求解算法的可行性与有效性进行验证。 鉴于保密限制,本文着重研究模型,不涉及相关人员与装备作战能力参数的具体信息。 想定作战背景与参数如下。 (1) 红方要点信息 数量NY=2。 要点1为某市区指挥所,相对保卫重要度E11=1;固定于市区,相对保卫难度系数E21=0.5;无防御工事,相对抗毁伤影响系数E31=0.2。综合保卫系数E1=E11E21E31=0.1。 要点2为某机场,相对保卫重要度E12=0.5;位置固定,相对保卫难度系数E22=0.5;机库具备一定防御工事,相对抗毁伤影响系数E32=0.4。综合保卫系数E2=E12E22·E32=0.1。 (2) 红方兵力信息 海上力量种类MH=2,其中战机编队H1与舰船编队H2各有40组,即NH1=NH2=40。 地导种类ML=2,1型地导L1和2型地导L2各20枚,即NL1=NL2=20。 (3) 蓝方兵力信息 (4) 蓝方兵力对各要点分配情况 (5) 已知红方对蓝方拦截概率P0如表1所示。 表1 红方对蓝方拦截概率表 (6) 蓝方毁伤能力 蓝方1型战机编队一次成功轰炸,对红方要点造成毁伤比率为1-WK1=0.2,WK1=0.8。 蓝方2型战机编队一次成功轰炸,对红方要点造成毁伤比率为1-WK2=0.4,WK2=0.6。 蓝方导弹一次成功打击,对红方要点造成毁伤比率为1-WD1=0.6,WD1=0.4。 (7) 双方主观综合能力比 红方与蓝方主观综合能力相同,即能力比w=1。故w修正后概率:P=1-(1-P0)w=P0 将第4.1节中相关参数代入第2.2.1节模型中,并按第3.1节处理流程,使用Matlab软件整数规划,求解得红方海上力量编队分配矩阵为 C1,1=C2,2= 0 20 20 0 使用式(15),求得针对各要点蓝方在海上拦截阶段成功突防的编队数量期望,对指挥所: 10-9.785 1=0.214 9 对机场: 10-9.785 1=0.214 9 其中,f(x)为满足期望μ=12,方差σ2=4.8的正态分布函数。 结果表明,红方海上力量最优兵力分配为:各分配20组战机编队拦截蓝方2型战机编队,分配20组舰船编队拦截蓝方1型战机编队。可达到最优效果为:对每个要点,蓝方战机突破红方海上拦截的1型编队和2型编队的数量期望各为0.215组。 将第4.1节中参数和第4.2节中计算所得数据带入第2.2.2节模型中,按第3.3节处理流程,使用Matlab软件整数规划,求解得红方地导兵力分配矩阵: 按照式(16)和式(17),求得蓝方能够对红方各要点成功打击的数量期望。 对指挥所可求得 其中,f(x)为满足期望μ=9.2,方差σ2=4.32的正态分布函数。 0.214 9-0.205 6=0.009 3 其中,f(x)为满足期望μ=0.8,方差σ2=0.16的正态分布函数。 0.214 9-0.180 7=0.034 2 其中,f(x)为满足期望μ=0.6,方差σ2=0.24的正态分布函数。 对机场可求得 结果表明,红方地导力量最优分配为:对每个要点,各分配10枚1型地导和8枚2型地导用于拦截蓝方导弹,分配1枚2型地导拦截蓝方战机1型编队,分配1枚2型地导拦截蓝方2型编队。整个联合防空作战可达到最优作战效果为:蓝方能对红方每个要点成功实施打击的数量期望同为1.29枚导弹攻击,0.009 3次1型编队轰炸,0.034 2次2型编队轰炸。 根据第4.3节所得结果,代入式(13)可得到此次联合防空作战中,指挥所剩余价值:D1=0.41.29×0.80.009 3×0.60.034 2=0.300 7;机场剩余价值:D2=0.300 7。代入式(14)和式(15)计算得所有要点作战价值的平均剩余: 以此作为本次联合防空作战的兵力分配效能评估值。结果表明,在红方兵力总数确定时,通过采用最优的分配方案,可以保证在与蓝方作战后,红方要点仍能发挥的作用价值不低于原有价值的30.07%. 立足于现代化联合作战行动,对近海小规模局部战争中联合防空作战的兵力分配及分配效能的评估进行研究。首先对实际的复杂作战情况进行抽象得到模型。在已知蓝方火力配置的条件下,通过采用分段建模优化,总体概率计算的方法解决了多过程作战的兵力分配优化问题。提出一种新的方法解决了有限制的类二项分布的期望求解问题。用此方法计算得到蓝方各类火力单元成功突防的数量期望,进一步得到红方要点作战价值的平均剩余期望,并以此值作为兵力分配防空效能的定量评估值,实现了优化与评估相统一。最后,通过一个想定的战例,进一步验证模型与求解理论的可行性与有效性。2.2 模型优化与评估


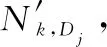
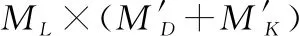
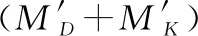
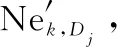
2.3 模型有效性分析
3 模型求解
3.1 海上力量分配求解
3.2 蓝方海上突防的真实期望求解
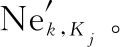
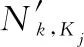
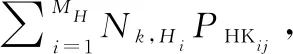
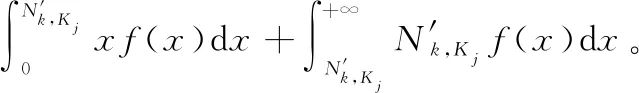
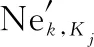
3.3 地导力量分配求解
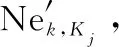
3.4 兵力分配效能估值求解
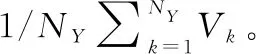
4 实例分析
4.1 背景想定
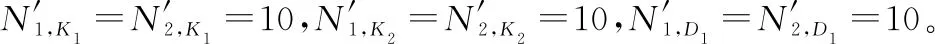

4.2 海上拦截阶段求解
4.3 内地反导拦截阶段求解
4.4 分配效能估值计算
5 结 论

