基于时频脊线和阶次分析的转子故障诊断

庾天翼，李舜酩，龚思琪

（南京航空航天大学能源与动力学院，南京 210016）

0 引言

转子在升速和降速过程中的转速变化会导致非平稳信号的产生。对于非平稳信号，通过信号采样获取的振动信号不再具有周期性，故无法采用传统的傅里叶变换进行信号处理和振动分析。传统振动信号分析包括振动信号获取、信号处理、信号特征提取、模式识别和智能决策，不适用于非平稳信号的故障诊断。因此，非平稳信号处理和分析方法成为了研究热点，同时，也引起了国内外故障诊断研究领域众多专家的关注。

变转速动态信号处理及故障诊断方法的主要研究技术路线是以阶次分析及其衍生方法为主。机械故障诊断领域著名学者澳大利亚新南威尔士大学Randall 和法国里昂大学Antoni指出：“阶次跟踪是解决变转速问题最为直接和有效的方法。”阶次分析实质上将非平稳的时域信号转换成平稳的阶次域信号，以此作为变转速机械设备故障诊断的判断依据。利用机械设备的转速信息将等时间间隔采样信号变换到等角度间隔的角度域信号，去除转速波动对时域信号的影响，在阶次域中观察平稳信号的图像，使得针对定转速信号的处理方法重新发挥作用。

近年来，中国对阶次分析的研究逐渐增加。王况等利用阶次分析技术对行星齿轮箱进行分析，并且深入分析了行星齿轮箱局部故障的不同阶次特征；冯珂利用计算阶次图谱和统计指标作为辅助手段，对Vold-Kalman 滤波器带宽进行筛选优选，提出了一种Vold-Kalman 阶次分析方法；杨武成提出了一种基于阶次跟踪和Hilbert 包络解调的滚动轴承故障诊断的新方法，用Hilbert 包络解调把低频故障信号从高频载波信号中解调出来，联合阶次跟踪有效地提取了时变工况下非平稳振动信号的故障特征频率并判断故障类型；武英杰等提出一种基于变分模态分解（Variational Modal Decomposition，VMD）滤波和极值点包络阶次的特征提取方法，可以有效提取调幅信号中的调制阶次，并且VMD 滤波使故障特征阶次更加凸显，易于故障识别。

由以上国内外现状可知，阶次分析法对采样系统硬件依赖性极高。当下机械设备日益集成化，设备中某些重要部位并不适合转速计的安装，在缺少振动信号和转速信号同步采样设备的状况下，阶次分析难以实现。为此，本文结合2 维时频分布的时频脊线技术和阶次分析方法，提出一种无需安装转速计即可实现阶次分析的新方法，对转子升降速信号进行故障诊断；并通过实测信号的对比试验，验证该方法的有效性。

1 非平稳转子信号故障诊断理论

1.1 阶次分析原理

阶次分析法是将时域非平稳信号转化为角度域平稳信号进行分析的方法。许多在时域、频域乃至时频域无法抑制、剔除的机械系统激振以及一些系统的随机误差，都可以在阶次域中抑制。而一些故障信息会在阶次域中得到较为清晰地显现，因此采用阶次分析法可提高故障诊断成功率。

阶次分析的基础就是转速信号，阶次表示为每周期事件发生的次数，是代表基于速度相关性振动的理想状态。阶次与转速、频率之间的关系为

式中：为阶次；为频率；为转速。

阶次分析的基础是振动信号的同步采样，同步采样的质量则依赖于取样系统的准确性和可靠性。阶次分析方法有硬件阶次跟踪和计算阶次跟踪等。硬件阶次跟踪的采样速率与转速成正比，确保信号采样频率与转速同步。计算阶次跟踪采用传统采样方法，异步采样采集到振动信号和转速信号，从异步采样的转速信号中，计算产生同步采样数据所需的等角度重采样时间。然后通过数据拟合或插值算法来对振动信号的这些时刻进行重采样，获得角度域信号，在对其进行快速傅里叶变换即可得到阶次图谱。

1.2 2维时频分布的时频脊线

对变转速振动信号进行时频分析后，一些与机械零部件动力学特性相关的曲线会清晰或隐约地出现，这些曲线在3 维时频空间内的分布形态与“山脊”很像，如脊线标志或沿脊顶延伸的线。因此，在3 维时频空间中把沿功率最高点延伸的线称之为时频脊线。时频脊线往往表现为时频面上的各种线条，包括直线、椭圆弧、抛物线、正弦曲线等，表征信号频率变化的各种模式。

对于1 个时频聚集性好且无交叉项的时频分布，信号的能量总是沿着瞬时频率集中分布，也就是说，时频分布的能量脊线总是出现在信号的瞬时频率附近。将3 维空间上的时频脊线投影到2 维空间中，可以观察到1 条函数曲线，这条函数曲线的每一点就近似乃至等于转子在某一时间点上对应的瞬时频率。因此可以将这条投影在2 维时频面的曲线称之为“时间—瞬时频率”曲线。

振动信号在时域和频域的能量可表示为

式中： ||()、 ||()分别为信号在时域和频域的能量密度。

同理，信号在时频域内的能量为

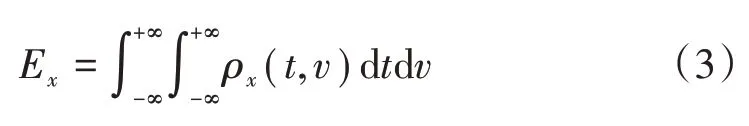
式中：ρ(,)为信号的时间频率密度，是2次型的函数。

能量分布还满足边缘性质

对于短时傅里叶变换来说，其时频脊线是指时频分布中每一时刻的峰值频率

式中：（，）为信号的时频分布。

时频脊线总是集中分布在变转速信号瞬时频率分量周围，故基于2 维时频分布的脊线提取方法包含2 个步骤：（1）将振动信号映射到时频域中；（2）采用峰值脊线提取法通过能量最高点提取信号的中心主频率，从2维时频面内识别出目标脊线。

2 非平稳转子信号故障诊断方法

2.1 基于时频脊线和阶次分析的转子故障诊断步骤

在缺少振动信号和转速信号同步采样设备的状况下，阶次分析难以实现。时频脊线表征信号频率变化的各种模式，频率变化即为转速变化，而且在映射过程和脊线提取过程中，信号的时间关系是同步的，因此时频脊线可以作为振动信号的同步转速信息使用。在仅仅采集到振动信号的情况下，采用基于2 维时频分布的脊线提取法对振动信号进行脊线提取，将时频脊线作为阶次分析法所需的同步转速信号，即可得到无需安装转速计的阶次分析方法。

基于时频脊线和阶次分析的转子故障诊断步骤如图1所示。

图1 基于时频脊线和阶次分析的转子故障诊断步骤

具体步骤如下：

（1）通过短时傅里叶变换（Short-Time Fourier Transform，STFT），将时域信号映射到时频域中，采用峰值脊线提取法获得时频脊线

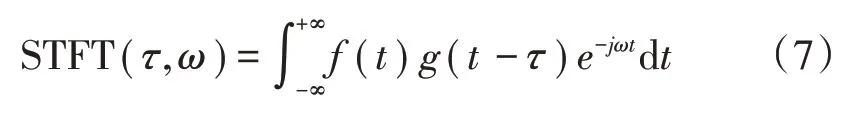
（2）进行卡尔曼滤波，对原始信号进行降噪预处理，结合提取出的时频脊线中的转速信息，对降噪信号进行等角度重采样，获得角度域信号

式中：（│-1）为利用前一状态预测的结果；（-1│-1）为上一状态最优的结果；（）为现在状态的控制量；（）为过程的噪声；为协方差；和为系统参数；（）为时刻的测量值；为测量系统的参数；为卡尔曼增益。

（3）将角度域信号映射至阶次域中，获得阶次图与阶次域信号，此为故障敏感特征；

（4）将敏感特征输入训练好的人工神经网络模型中，对转子信号的故障类型进行分类。

2.2 转子典型故障及其敏感特征

转子的常见故障主要有转子不平衡、转子不对中和转子碰摩等。转子碰摩故障往往源于转子不平衡和不对中故障，本文不做讨论。

转子不平衡是转子故障中的常见故障之一。不平衡是质量和几何中心不重合所导致的故障，转子不平衡时偏心如图2所示。

图2 转子不平衡时偏心

转子不对中也是转子故障中的常见故障之一。转子不对中分为平行不对中、偏角不对中和平行偏角不对中3种，如图3所示。

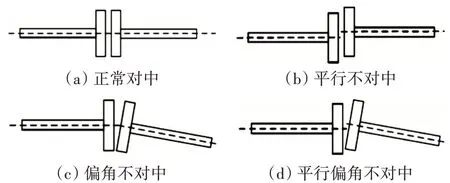
图3 转子不对中

阶次域中转子轴典型故障的敏感特征见表1。

表1 阶次域中转子轴典型故障的敏感特征

3 试验验证

3.1 试验数据采集

本文采集转子升速和降速过程中的振动信号作为试验数据。试验台在0~5000 r/min 的转速下工作，采用脂润滑方式。电机参数的额定功率为0.75 kW，额定电压为380 V，额定转矩是5.0 kN·m。

试验台和传感器安装位置如图4所示。轴上的2个盘是为产生转速波动的扭转振动信号而加装的平衡盘。图4（a）通过在大盘加装质量块产生不平衡故障，图4（b）通过垫高右侧支架产生不对中故障。采用2 个加速度传感器同时测量轴输入输出端数据，传感器型号及参数见表2。

图4 转子试验台

表2 传感器型号及参数

试验台所采用的数据采集系统为LMS 系统，其采样频率为51200 Hz，带宽为12800 Hz，分辨率为0.25 Hz。根据转速和采样频率可知信号在1 个周期（即试验台旋转1 周）所采得的数据点为3413 个。测试工况为缓加速，通过手动调节电机变频器至最大转速实现。

3.2 信号敏感特征对比

试验台测得2 组故障信号数据，从每组信号中选取4096 点进行分析。分别采用传统敏感特征提取法与阶次分析敏感特征提取法，提取并对比2 组信号的敏感特征，判断阶次分析法的效果。

3.2.1 传统敏感特征提取法

传统分析方法仅对信号进行降噪处理，再转化到频域中进行分析。转子不平衡、不对中信号传统敏感特征如图5、6所示。

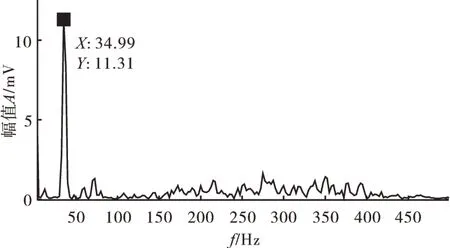
图5 转子不平衡信号传统敏感特征

从图5 中可见，计算转速频率约为35 Hz，图中最大峰值出现在35 Hz 附近，是由于不平衡故障信号特征表现出的1X倍频，是不平衡故障敏感特征。

从图6 中可见，计算转速频率约为85 Hz，在84.98、160、272.4和339.9 Hz附近分别表现出1X、2X、3X 和4X 倍频，根据转子不对中故障信号敏感特征可判断，该信号具有转子不对中故障特征。

图6 转子不对中信号传统敏感特征

3.2.2 阶次分析敏感特征提取法

以转子不平衡信号为例详细说明阶次分析法，并给出不平衡、不对中2组信号的阶次域图像。

3.2.2 .1 基于2维时频分布的时频脊线提取

对原始时域信号进行STFT，设置采样频率为12 kHz，海明窗函数长度取为256，为了提高计算精度，取2 窗函数之间的重叠采样点为250。得到时频谱如图7所示。

从图中可见在时频面内信号的时频特性，对比右侧颜色等高线，观察到试验信号的高频分量相对较少，可以将其忽略不计，而在低频分量上，时频图中的能量分布较高，可知试验装置的敏感特征主要存在于低频分量中，可重点关注图中的低频分量区。

在图7中存在一些或清晰或隐约的曲线，尤其是在低频分量范围有一片明显的明亮带，说明在其附近一定存在峰值，如果将这些峰值连成线，即可得到所需时频脊线。提取信号能量值最高点，之后再进行曲线拟合，如图8所示。

图7 时频谱

试验工况为缓加速，因此图8 中红色拟合曲线呈现上升态势，频率随时间缓缓升高。对比试验采集过程中转速变换趋势，这条2 维时频脊线与其吻合度极高，可以作为振动信号转速信息用于下一步的阶次分析。

图8 时频脊线

3.2.2 .2 基于等角度重采样的角度域变换

对转子故障振动信号进行等角度采样，即可得到角度域信号。从图5 频域中可知，虽然经过卡尔曼滤波后剔除大部分杂波，但是其中还存在很多杂乱的信号波纹，可能包含信号传递过程中由于机械结构激振出的信号分量和无法完全过滤掉的杂波，且转速的波动变化也会产生非平稳信号，因此将信号由时域转换到角度域中进行观察，是机械故障诊断分析中重要一步。

以瞬时频率为基础的等角度重采样，重构了滤波后的原始信号，将非平稳的时域信号转变为角度域平稳信号，有效抑制了随机噪声和无关周期分量的干扰，可以更清晰地观察到所需的敏感特征。结合提取出的时频脊线，对滤波重构后的时域信号进行等角度重采样，生成角度域特征信号，如图9所示。

图9 角度域特征信号

从图中可见，图像波形比时域波形相对集中，而且可以清楚地观察到其主要集中几段波形内，峰值也处于其中一处波形内。相对于主要波形，其他大多数范围内的波形都相对较小，可以很明显地区分出其只是一些不重要的分量，可以相对忽略不计。

3.2.2 .3 阶次域信号分析

对生成的角度域信号进行STFT，得到角度1 阶次域图像，如图10所示。

进一步将角-阶域（图10）的结果映射到阶次谱上，得到转子振动信号的阶次谱，如图11 所示。与原始信号图像相比较，可见阶次谱中出现了清晰典型的谱线峰值。

图10 角-阶域谱

图11 阶次谱

将图10、11 综合对比分析，可见在图10 中低阶次区内存在1 条近似水平的直线，将其命名为线1；在高阶次区同样存在1 条近似水平的线，将其命名为线2。在将角1 阶次谱投影到阶次轴上后，线1、2 均为峰值谱线（图11）。线1对应1阶幅值，线2对应高阶幅值，与前文介绍的阶次域中典型的不平衡故障特征相符，可以判断出发生了不平衡故障。

按照相同的步骤，转子不对中信号的阶次谱如图12 所示。

图12 转子不对中信号阶次谱

从图中可见，1、2 阶幅值突出，与转子不对中故障特征相吻合，说明发生了转子不对中故障。

与传统故障诊断法对比，阶次分析法获得的敏感特征更加清晰突出，噪声与转速波动产生的特殊频率对诊断过程的影响较小，便于进行故障诊断分析。

3.3 基于BP-ANN的故障诊断

根据第3.1 和3.2 节的诊断步骤，使用BP 人工神经网络（BP-Artificial Neural Network，BP-ANN）进行故障识别。通过对比试验，验证阶次分析方法在故障诊断中的有效性。

转子正常、不平衡故障、不对中故障数据集见表3。每个样本的采样点为4096，数据集共包含1200个样本，随机选择其中600 个样本作为训练样本集，其余600 个样本作为测试样本集，为了方便表示，将状况类别标签设置为1、2、3。

表3 数据集描述

设置BP-ANN 参数，中间结果周期为50，最大迭代次数为500，训练目标误差为0.001，学习率为0.001。为了消除随机性的影响，每组试验分别进行20次。

阶次分析方法的20次诊断准确率结果如图13所示。从图中可见，数据集的训练准确率均为100%，测试准确率超过99%，说明阶次分析方法可以准确诊断出升降速过程中转子的健康状态。

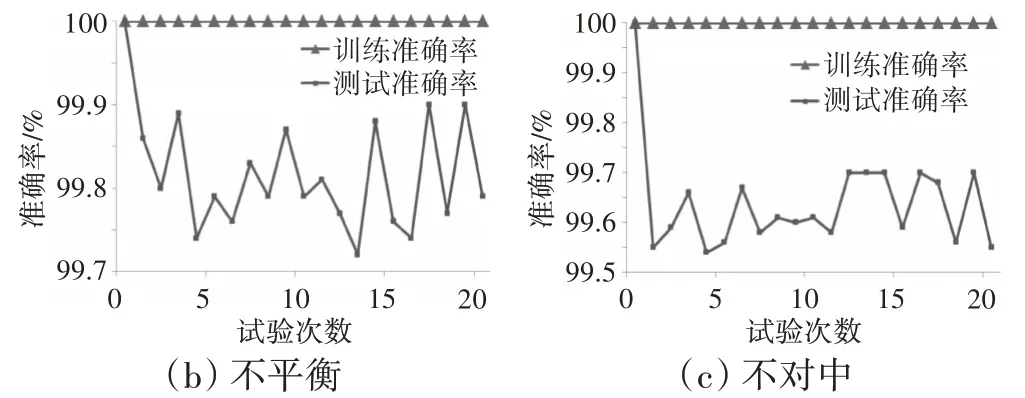
图13 阶次分析方法的20次诊断准确率结果

为了说明阶次分析方法的有效性，采用传统方法进行对比验证，该方法同样使用表3 的数据集。计算2 种方法的平均训练准确率与平均测试准确率，见表4。从表中可见，阶次分析方法的测试准确率稳定于99.62%~100%，标准差小于0.09%，均优于传统方法。

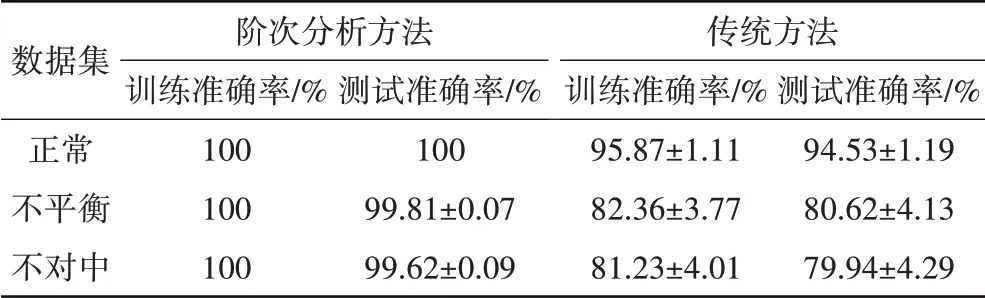
表4 阶次分析方法与传统方法诊断结果对比

4 结论

（1）提出一种基于时频脊线和阶次分析的转子故障诊断方法，并在人工诊断和机器诊断中获得理想的应用效果；

（2）在3 维时频空间中，信号能量沿着瞬时频率集中分布，通过连接时频分布中每一时刻的峰值频率获得2维时频脊线；

（3）基于2维时频分布的脊线提取法获得的时频脊线是振动信号的同步转速信号，且与实际转速对比吻合度高，可以作为同步转速信息，用于阶次分析。