面向空间插值的采样点数据空间聚集程度的度量方法



摘 要:为了探讨采样点数据聚集程度对于空间插值的影响,本研究采用蓝田县部分区域DEM数据为原始数据,使用多种采样方式模拟了150组具有不同空间聚集强度的试验数据集。建立了一种度量样本数据集空间聚集程度差异的方法,对比不同样点数、不同聚集程度采样数据集普通克里金法(Ordinary Kriging,OK)插值精度的差异。结果表明:相同样点数目情况下,空间聚集程度较高的样点集插值精度小于空间聚集程度较低的样点集;且随着样点数目增加,聚集强度差异对于OK插值精度的影响逐渐减小。故在样点数量较少时,样点集聚集程度的识别和处理对于提高OK插值精度尤为重要。
關键字:普通克里金;采样方式;样点聚集程度;插值精度
中图分类号:S159.9 文献标志码:A 文章编号:1003-5168(2022)1-0125-04
DOI:10.19968/j.cnki.hnkj.1003-5168.2022.01.028
Spatial Interpolation-Oriented Measure of Spatial Aggregation of Sampled Point Data
WANG Xiang1,2
(1.School of Earth Science and Resources, Chang'an University, Xi'an 710064,China;2.Research Center of Information Technology, Beijing Academy of Agriculture and Forestry Sciences, Beijing 100097,China)
Abstract: In order to investigate the influence of data aggregation degree on spatial interpolation, this study used DEM data of some areas in Lantian County as the original data, and simulated 150 experimental data sets with different spatial aggregation strength using various sampling methods. A method was established to measure the differences in spatial aggregation of the sample data sets, and the differences in the interpolation accuracy of ordinary kriging (OK) were compared for different sets of data with the same number of points and different degrees of aggregation. The results show that the interpolation accuracy of the sample data set with higher spatial aggregation is smaller than that of the sample data set with lower spatial aggregation, and the effect of the difference in aggregation intensity on the interpolation accuracy of OK decreases as the number of sample points increases. Therefore, when the number of sample points is small, the identification and processing of the aggregation degree of the sample point set is especially important to improve the OK interpolation accuracy.
Keywords: ordinary kriging; sampling method; sample point aggregation;interpolation accuracy
数字空间制图是对地理要素空间分布特征的反映[1],体现地理要素的形成与发展过程,在环境科学研究中具有广泛的应用。其制作过程大致分为四步:获取研究对象数据、确定采样方法与策略、选择制图模型方法、生成研究对象的数字化图像[2]。获取研究数据过程十分重要,地学研究中环境要素数据信息的获取比较困难,受到人力、物力、财力、研究区状况等客观因素的限制,样点数量不可能无限多,通过采样检测的方式获取研究对象的特征是环境科学研究常用的方法[3],但研究者要获取的不仅仅是有限的采样点处的研究对象的信息,更关注研究对象在空间的连续变化情况。如环境污染研究人员需要了解土壤中重金属含量的连续变化情况,有针对性地开展污染治理工作;地貌地形研究人员不仅仅需要有限采样点的高程、坡度,更关注地形在空间的连续变化情况。
空间插值技术就是根据给定的采样点数据及其空间位置,拟合出一个能充分反映对象特征与空间位置间的数学关系的函数方程,从而获得研究对象在整个研究区域空间上的连续分布情况。OK是一个确切估计器,使得其估计的随机场在样本点的取值与对应观测值一致[4],其他空间点的估计不会与实际情况相距太远;这一优势使得OK法在环境科学领域、气象、土壤、生态、水文等领域具有广泛的应用[5]。OK插值精度受制于多种因素的影响。采样数目、采样密度等都会影响OK插值过程及结果,进而影响通过空间插值分析地理要素特性的空间分布和变异规律[6-11]。但是目前针对样点空间分布对于OK插值影响的研究还比较少,本研究利用多种采样方式模拟不同聚集程度采样数据,提出了一种度量采样点数据空间聚集程度的方法,分析样点数据集的样点空间聚集程度对OK插值精度的影响规律,可为耕地质量评价、土壤污染详查等领域空间制图提供理论借鉴。
1 研究区概况和数据来源
1.1 研究区概况
蓝田县位于西安市东南。本研究所采用的高程数据取自蓝田县东北的矩形区域,地理位置在北纬33°84′—33°97′,东经109°07′—109°49′,东西长为10 km,南北宽为14 km,总面积为140 km2。研究区域北部连接横岭余脉,东南部毗邻秦岭山地,西部为平原,整体走势呈现东高西低,境域内最高点海拔为1 709 m,最低点海拔为211 m,平均海拔约为950 m。研究区域内高程地形多样,既包括平原等地形简单区域,又包括山地等地形变化复杂区域,在此区域内采样能较好地模拟复杂多变地理要素的采样过程,获得真实可靠的试验数据。
1.2 数据来源及预处理
DEM数据来源于ASF Data Search平台,分辨率为12.5 m,通过对研究区域DEM进行不同方式采样,获得多种聚集分布状态的样点数据集。根据等高线密集程度的差异,选择目的性采样、分层采样、随机采样三种方式,按照100点、300点、500点、700点、900点分别实现10次采样,共获得150个试验数据集,通过提取分析等处理,使用含高程属性的采样点模拟真实采样数据进行样点空间聚集强度度量研究。
2 研究方法
2.1 采样数据聚集程度表征方法
空间聚集因子(Cluster Factor,CF)表示样点数据空间聚集度,公式见式(1)。
式中,对样点创建泰森多边形,n为对多边形面积聚类后得到的最小类泰森多边形的个数;si为n个多边形中第i个的面积;S为研究区总面积;N为样本总数;CF∈(0,1),样点在研究区域内完全均匀布时,CF=1;当样点存在空间聚集情况则0<CF<1,最小类的泰森多边形个数越多、面积越小则值越小,样本数据集聚集程度越大;随着聚集程度加深,CF值逐渐趋近于0;样点完全均匀分布CF=1。
地理空间特征呈现聚集分布的样点的泰森多边形会呈现面积小且相邻的特点,故利用样点在研究区域生成的泰森多边形,以泰森多边形面积为属性进行K-means聚类,当面积较小且空间邻接的泰森多边形聚集在一起,它们所代表的样点在空间分布上亦聚集。针对各样点数量级下的试验样点集空间聚集程度的差异,利用K-means聚类算法将其划分成K类。其中,K-means聚类算法是以距离作为相似性评价指标,指定K个初始聚类中心,根据样本之间的距离划分成K类。利用局部Moran′sⅠ系数将样点泰森多边形面积的空间格局可视化,不断调整聚类数K。当K-means聚类法结果中的最小类与低值聚集区域(LL)范围相同或相似时,该区域代表的样点在空间特征上亦呈现聚集分布状态。
2.2 空间插值方法及插值结果精度評价
2.2.1 空间插值方法。OK是以变异函数理论和结构分析为基础的一种常见空间插值方法,在区域变量存在空间自相关的前提下,根据未知点和其一定范围内采样点的距离及空间关系拟合模型确定权重,对区域内未知点的属性进行线性无偏、最优估计。无偏最优估计也就是使估计值等于实际值的数学期望,且方差最小[12]。
2.2.2 插值结果精度评价。本研究利用3种采样方式获取不同空间分布状态的含高程属性的点数据,在具有真实DEM的情况下,采用平均绝对误差(Mean Absolute Error,MAE)来定量描述不同聚集程度样点数据对于空间制图的影响。平均绝对误差计算公式为
3 结果与分析
3.1 样点数据空间聚集计算结果
计算150个样点集的空间聚集因子并按照从小到大、分样点数量绘制空间聚集因子离散图。经过计算得到150个样点集的空间聚集因子,其中300、500点样点集的空间聚集因子值按升序排列后呈现两个阶梯;而100、700、900样点数呈现三个阶梯。
3.2 相同样点数量、不同聚集程度样点空间插值结果精度对比
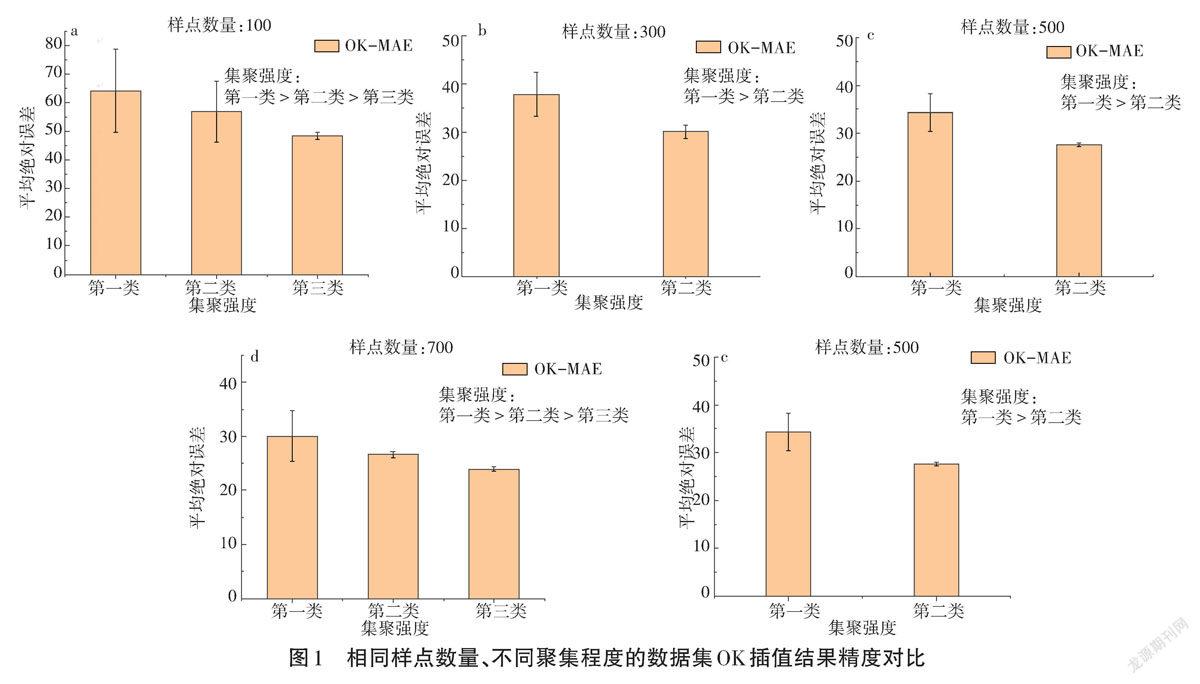
基于图2中各样点集空间聚集因子的分布状况,将100、300、500、700、900样点的30个数据集按照聚集程度分别划分成3类、2类、2类、3类、3类(图1),计算并统计相同样点数量下同类别数据集OK插值结果的MAE。本研究首先利用SPSS.24统计分析软件剖析了150个数据集高程值的统计特征,为满足OK插值需求,通过Box-Cox变换使之达到或近似正态分布;在此基础上使用GS+7.0软件进一步计算了各个试验数据集的半变异函数参数;最后在ArcGIS10.6软件的支持下,生成预测栅格,对比分析不同样点数量、不同样点聚集程度下的预测精度的差异。
样本点聚集程度差异对于OK插值结果的平均绝对误差的影响如表1所示,当样点数量为100时,第一类样点集OK插值结果的MAE为58.180;第二类为56.852,第三类为48.525。插值精度:第一类<第二类<第三类;聚集强度:第一类>第二类>第三类。同理,300、500、700、900样点数量的样点集亦均表现出样点聚集强度越高,插值精度越差,平均绝对误差越大的趋势。100样点聚集强度较高的数据集MAE均值与聚集强度较低的数据集MAE均值的差值为9.655,900样点聚集强度较高、较低数据集间MAE均值的差值为1.759。结果表明:低聚集采样数据插值精度明显优于高聚集;且随着样点数量增加,不同聚集强度样点集的OK插值结果MAE差异逐渐减小。
随着样点数量增加,OK插值精度不断提高,样点数量为100时(30个数据集)OK插值结果的平均MAE为55.229,样点数量为500时MAE为30.599,样点数量为900时MAE为25.292。明显表明增加样点数量能有效提升插值精度,但是此过程并非线性递增。样点数量由100点增加到300点时OK插值结果精度得到明显的改善,增加200个样本点,MAE减小了33.282%。但由300点增加到900点时,增加600个样本点,OK插值结果精度虽仍在提升,但提升的幅度并不大,MAE分别仅减小31.161%。
综上所述,提升样点数量能有效提升插值结果精度,但存在阈值。超过阈值继续增加样点数目对于改善插值结果精度的效果不再显著;聚集程度较低的样点集空间插值精度优于较高的数据集,随着样点数量增加,聚集程度差异对于OK插值结果的MAE影响越来越小。
4 结论
本研究基于DEM数据,模拟了不同样本点数量(100、300、500、700、900)、不同聚集程度样点集,应用普通克里金法进行空间插值。阐述采样数据空间聚集差异对于OK插值精度的影响,高聚集样点数据的插值结果MAE明显大于低聚集样点数据,且在样点数较少的情况下差异尤为明显。研发的面向空间插值的采样点数据空间聚集程度的度量方法,可以判断判断多个数据集间的聚集程度差异,可以为采样数据去冗精化提供借鉴,服务于面源与重金属污染、耕地质量检测、地下水和地表水中的污染物浓度分析等领域。
参考文献:
[1] 李莹莹,赵正勇,杨旗.数字土壤制图在土壤养分方面的研究综述[J].江西农业学报,2021,33(7):61-67.
[2] 朱阿兴,杨琳,樊乃卿,等.数字土壤制图研究综述与展望[J].地理科学进展,2018,37(1):66-78.
[3] 陸安详,曹珊珊,高秉博.面向农业环境监测的空间插值方法[M].北京:经济科学出版社,2017.
[4] LE N D, ZIDEK J V. Statistical analysis of environmental space-time processes[M]. Springer Science & Business Media, 2006.
[5] 高秉博,郝朝展,李发东,等.面向土壤环境质量等级划分的统计推断与加密采样优化方法研究综述[J].农业环境科学学报,2021,40(4):712-722.
[6] ERICSON B,CARAVANOS J,CHATHAM-STEPHENS K,et al. Approaches to systematic assessment of environmental exposures posed at hazardous waste sites in the developing world:The toxic sites identification program[J]. Environmental Monitoring and Assessment,2013,185(2):1755-1766.
[7] 张贝尔,黄标,赵永存,等.采样数量与空间插值方法对华北平原典型区土壤质量评价空间预测精度的影响[J].土壤,2013,45(3):540-547.
[8] 巫振富,赵彦锋,程道全,等.样点数量与空间分布对县域尺度土壤属性空间预测效果的影响[J].土壤学报,2019,56(6):1321-1335.
[9] 庞夙,李廷轩,王永东,等.县域农田土壤铜含量的协同克里格插值及采样数量优化[J].中国农业科学,2009,42(8):2828-2836.
[10] 李润林,姚艳敏,唐鹏钦,等.县域耕地土壤锌含量的协同克里格插值及采样数量优化[J].土壤通报,2013,44(4):830-838.
[11] 赵业婷,常庆瑞,李志鹏,等.基于Cokriging的耕层土壤全氮空间特征及采样数量优化研究[J].土壤学报,2014,51(2):415-422.
[12] 靳国栋,刘衍聪,牛文杰.距离加权反比插值法和克里金插值法的比较[J].长春工业大学学报(自然科学版),2003(3):53-57.
收稿日期:2021-12-26
基金项目:科技部重点研发计划课题“黑土地耕地质量时空多维大数据预警系统研发”(2021YFD1500104)。
作者简介:王翔(1994—),男,硕士生,研究方向:空间数据处理与分析。
3688500338221

