基于瞬时频率响应函数的间歇过程时段划分

李宇斌，于 涛

(北京化工大学信息科学与技术学院，北京 100029)

0 引 言

间歇过程经常用于生产高附加值的产品，在生物制药、食品加工、聚合物反应及半导体生产等诸多领域具有广泛应用[1-3]。间歇过程复杂多变，容易受各种因素的影响，一些微小故障的存在就可能导致产品质量降低，甚至产生安全隐患。对间歇过程进行有效的故障监测，对确保生产安全，保证经济效益具有重要意义。多时段特性是间歇过程的本质之一，间歇过程不同时段内的变量特征不尽相同，需要对各个时段分别建立模型来描述过程特性。因此，正确有效地对多时段间歇过程进行时段划分，对过程监测和阶段建模具有重要意义[4-7]。

目前，针对间歇过程的时段划分方法，基于过程变量数据多元统计分析的时段划分方法应用最为广泛[8]。多向主元分析(Multi-way Principal Component Analysis， MPCA)[9]和多向偏最小二乘(Multi-way Partial Least Squares， MPLS)[10]是基于过程变量多元统计分析的时段划分方法的基础。Lu等[11]对间歇过程时间片矩阵进行主元分析(Principal Component Analysis， PCA)得到反映过程相关性的负载矩阵，利用K-means算法对负载矩阵聚类，划分时段；Lu等[12]利用K-means聚类对间歇过程时间片矩阵的偏最小二乘(Partial Least Squares， PLS)回归参数矩阵进行聚类分析，划分时段，能够确定过程变量在特定阶段对产品质量的影响；于涛等[13]提出一种基于滑动时间窗加权MPCA的时段划分方法，对间歇过程数据通过滑动窗和加权处理得到局部特征，利用K-means聚类划分时段，降低了非平稳过程对时段划分的影响；高学金等[14]对间歇过程时间片矩阵进行核熵成分分析，得到主元，完成初次阶段划分，利用模糊C均值聚类(Fuzzy C-means， FCM)对添加时间片矩阵的扩展核熵负载矩阵的相似度聚类进行二次阶段划分，有效克服了时段划分过程跳变点错分的现象。以上时段划分方法是基于过程变量多元统计分析实现的，对过程变量数据突变较为敏感。

频率响应函数(Frequency Response Function， FRF)反映了系统的动态特性，具有广泛的应用[15]。Zenzen等[16]将FRF和蝙蝠算法相结合，实现了对桁架结构损伤位置和严重程度的检测；单卫东等[17]利用FRF识别直升机尾传动轴系非线性模态参数；李志农等[18]将非线性输出FRF用于转子不对中-碰摩耦合故障诊断，能够识别不对中的严重程度；Lin等[19]建立了高阶FRF和裂纹物理参数之间的联系，使用二阶FRF识别呼吸裂纹的物理参数。

间歇过程数据具有高维度、非线性的特点。核主元分析(Kernel PCA， KPCA)经常用于非线性高维数据的降维和特征提取[20]。梁京章等[21]将KPCA与融合密度思想的K-means算法相结合，实现非线性电力负荷曲线的有效降维和精确聚类；王玲等[22]利用KPCA提取多元时间序列特征，结合Gath-Geva聚类实现多元时间序列的模糊分段；Ding等[23]利用KPCA对网络数据降维，缩短了反向传播神经网络的训练时间，提高了网络入侵检测的速度。

传统的时段划分方法针对间歇过程的过程变量数据划分时段，对输入输出数据突变较为敏感。本文基于小波变换估计间歇过程的瞬时频率响应函数(Instantaneous FRF， IFRF)，利用基于间歇过程的瞬时动态特性进行时段划分，提出基于IFRF的划分方法。该方法通过小波变换估计系统的IFRF并进行KPCA降维，利用FCM进行聚类分析，实现基于小波域IFRF的间歇过程时段划分。

1 基于非线性MPCA的间歇过程时段划分

1.1 间歇过程样本数据展开

间歇过程作为典型的批处理过程，其过程数据可以表示成一个三维张量F(I×J×K)，其中I为批次个数，J为变量个数，K为单批次的采样点个数。在对间歇过程数据进行处理时，通常需要将张量数据展开成二维矩阵，按批次展开、按变量展开和按时间展开是最为常用的3种展开方式。按批次展开为：Fi(J×K)，每个切片矩阵表示为第i个批次内全部J个变量在全部K个采样点的数据，其中i=1,…,I；按变量展开为：Fj(I×K)，每个切片矩阵表示为第j个变量在全部I个批次全部K个采样点的数据，其中j=1,…,J；按时间展开为：Fk(I×J)，每个切片矩阵表示为第k个采样点变量全部I个批次全部J个的数据，其中k=1,…,K。间歇过程的时段划分具有一定的时间规律性，因此本文采用按时间展开的方式对间歇过程数据进行展开。

1.2 基于KPCA的数据降维

PCA方法是一种有效的线性数据降维方法，它能够用一组互不相关的主元代替原始数据，这些主元是原始数据的线性组合，包含原始数据的主要信息。

为了消除数据中量纲的影响，需要对数据集X进行标准化处理。假设对原始数据标准化处理后得到矩阵X=[x1，x2，…，xN]，xj∈RM，(j=1,2,…,N)，N为样本数量，M为变量个数。协方差矩阵为：

(1)

对协方差矩阵进行特征值分解，λ为特征值，p为特征向量。按累计方差贡献率来确定主元个数v，则PCA降维后的数据矩阵为：

T=XPv

(2)

PCA降维主要用于线性数据的降维，处理非线性数据的能力较差。KPCA方法在PCA方法的基础上引入核函数，是对PCA方法的非线性扩展。KPCA方法通过非线性映射将原始数据投影到高维空间，将线性不可分数据转化为线性可分数据，之后再对高维数据进行线性PCA降维处理。

计算协方差矩阵为：

(3)

λp=Cp

(4)

(5)

其中，α1，α2，…，αN为常数。引入N×N维核函数矩阵：

Kij=K(xi,xj)=Φ(xi)TΦ(xj)

(6)

则有：

Nλα=Kα

(7)

其中，α是核矩阵K的特征向量。对特征向量p进行归一化后，可得到原始数据经过非线性映射后在第m个特征向量pm上的投影为：

(8)

应用KPCA，通常需要对核矩阵K进行处理实现高维空间中心均值化，处理方式如下:

(9)

其中，IN为系数为1/N的N阶单位矩阵。

1.3 基于FCM的时段划分

FCM聚类是一种无监督聚类算法，其引入隶属度函数，通过隶属度的大小对数据点进行分类，定义如下：

(10)

聚类中心为：

(11)

第j个数据xj对第i类的隶属度函数为：

(12)

基于非线性MPCA的间歇过程时段划分通过使用FCM对KPCA降维后的数据矩阵进行聚类分析来实现，具体步骤如下：

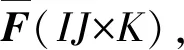
2)对矩阵Fv进行FCM聚类，得到第k个采样点数据对第l类的隶属度函数ulk，根据隶属度函数划分类别，实现时段划分。

2 基于IFRF的间歇过程时段划分

多时段特性是间歇过程的本质特性之一。频率响应函数反映了系统的动态特性，基于IFRF的间歇过程时段划分针对系统的瞬时动态特性进行时段划分。

2.1 基于WT的IFRF估计

频率响应函数是系统中输出信号和输入信号的频域形式之比，描述了系统的动态特性。对于瞬态激励系统，通常采用输出信号和输入信号的傅里叶变换(FT)之比来估计FRF。

利用FT估计系统的FRF，具体形式如下：

(13)

FT将时域信号转换为频域信号，只保留了频域信息，而丢失了时域信息。因此基于FT估计FRF无法反映系统的FRF随时间的变化。用小波变换(WT)代替傅里叶变换能够解决这个问题。

对于单输入单输出(Single Input Single Output， SISO)系统，使用小波变换估计其FRF为：

(14)

WT(k,ω)[y(k)]和WT(k,ω)[x(k)]分别为输出信号和输入信号的小波变换时频表示。

在输入输出信号中经常存在高斯白噪声，设w(k)～N(0,σ2)，此时有：

(15)

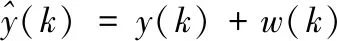
(16)

进行WT，可得到：

(17)

(18)

式中，WT(k,ω)[w(k)]为高斯白噪声的小波变换时频表示，且:

E|WT(k,ω)[w(k)]|2=σ2‖ψ‖2

(19)

其中，ψ表示为小波基函数。

得到基于WT的FRF如下：

(20)

在数值实现时，经常采用互功率谱法估计FRF。输入信号的自功率谱和输入输出信号的互功率谱如下：

(21)

(22)

其中，*表示复共轭。

基于WT自相关和互相关功率谱估计FRF为：

(23)

则H(k,ω)中，第k时刻对应的所有数据即为当前时刻的IFRF。

对于多输入多输出(Multiple Input Multiple Output， MIMO)系统，假定有R个输入、S个输出，每个输入对每个输出都存在对应的FRF，定义第r个输入对第s个输出的FRF为Hrs(k,ω)，其中1≤r≤R，1≤s≤S。Hrs(k,ω)中，第k时刻对应的所有数据即为当前时刻第r个输入对第s个输出的IFRF。

MIMO系统基于WT的FRF表示为：

(24)

进一步处理有：

(25)

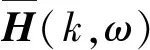
2.2 基于IFRF的间歇过程时段划分

基于IFRF的间歇过程时段划分采用IFRF替代间歇过程数据进行时段划分，并结合KPCA算法降维和FCM算法聚类划分间歇过程时段。

基于IFRF的间歇过程时段划分步骤如下：

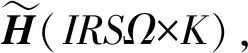
(26)

3 实验与结果分析

本文设计具有2个时段的数值仿真过程验证基于IFRF的时段划分方法；并将该方法应用于青霉素发酵过程仿真实验数据的时段划分，验证基于IFRF的时段划分方法的鲁棒性。

3.1 数值仿真实验

本文设计具有2个时段的数值仿真过程，如表1所示。

表1中，v1为输入变量，v2、v3、v4、v5为输出变量，构成一个单输入四输出系统。u为边界值为[2,3.5]的均匀分布，ζ～(0,0.2)为高斯白噪声，i为批次，k为采样时刻。

采集多批次具有120采样点的数据，前50采样点为时段1，后70采样点为时段2，采用本文方法进行时段划分，结果如图1所示。

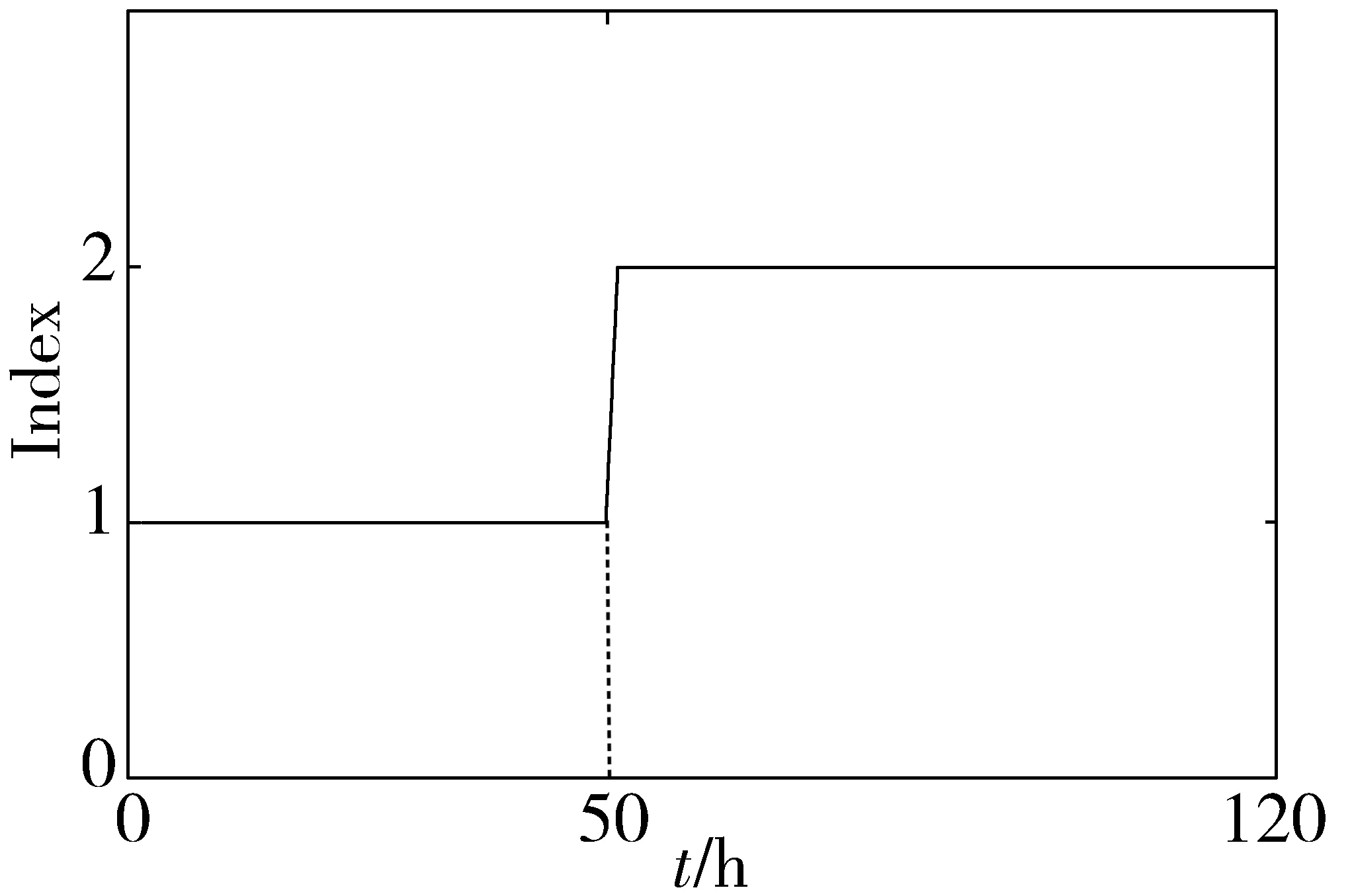
图1 时段划分结果

从图1可以看出，此过程划分为2个时段，分段点为50，与真值一致，验证了基于IFRF的时段划分方法的有效性。

3.2 青霉素发酵过程实验

青霉素发酵过程是经典的间歇过程，本文利用Pensim仿真平台生成青霉素发酵过程仿真数据，设置每批次时长为400 h，采样时间间隔为1 h，生成正常批次数据和底物流加速率在200 h～300 h时存在不同幅度阶跃突变的批次数据。选择底物流加速率作为输入变量，底物浓度、菌体浓度、青霉素浓度、发酵液体积、二氧化碳浓度作为输出变量，组成单输入多输出系统。

采用基于非线性MPCA的时段划分方法对以上数据进行时段划分，正常批次过程数据展开向量强度图如图2(a)所示，降维后的特征向量强度图如图2(b)所示。

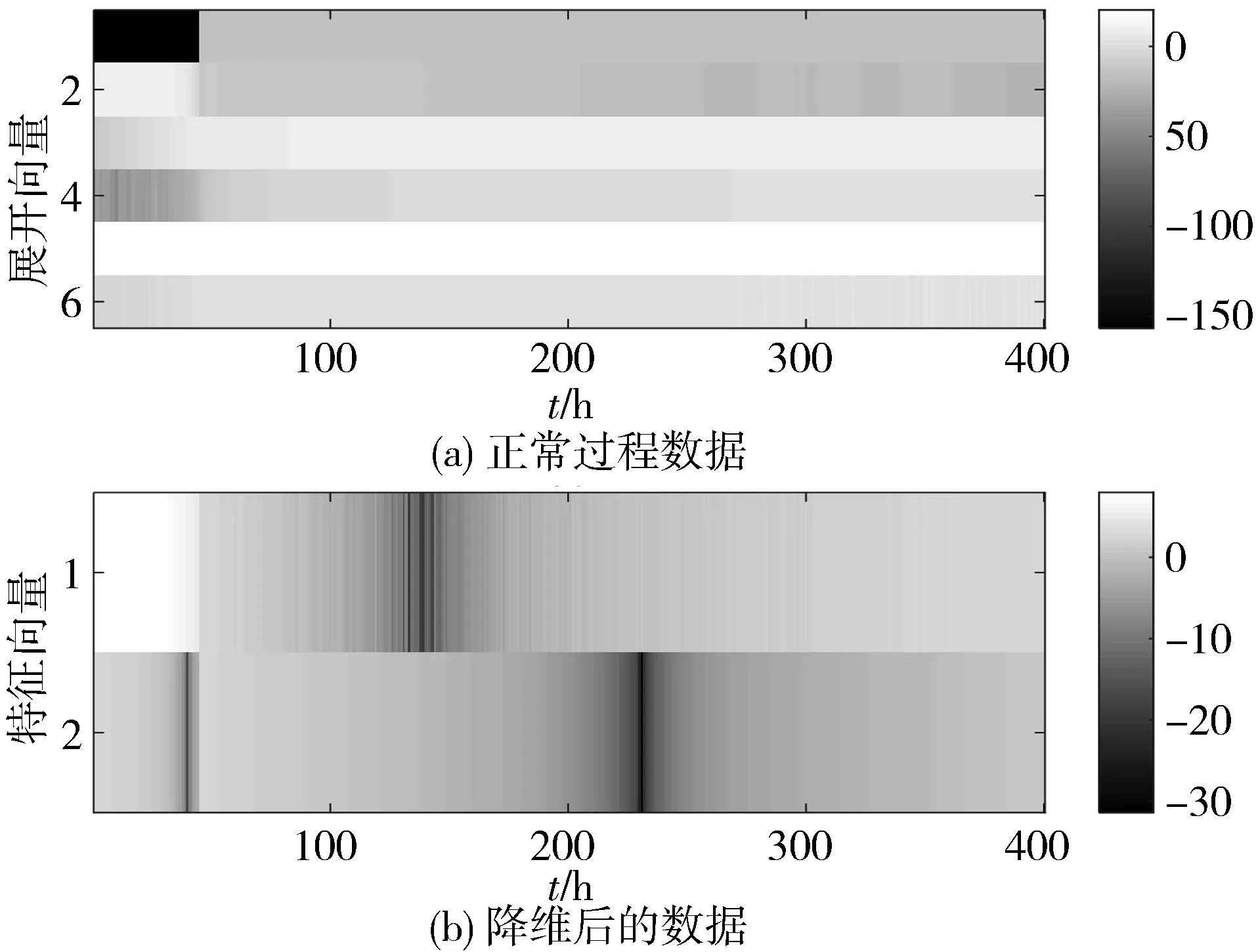
图2 过程数据向量强度图

从图2的过程数据强度图可以初步看出，间歇过程在100 h前存在一个较为明显的分段点。结合间歇过程先验知识，将间歇过程划分为3个时段，各个突变幅度数据的时段划分结果如图3所示，时段划分的分段点如表1所示。

图3 基于非线性MPCA的青霉素发酵过程时段划分结果

从图3和表2可以看出，在底物流加速率存在不同幅度的阶跃突变时，基于非线性MPCA的时段划分方法的划分结果中，分段点1和分段点2都存在波动，且分段点2变化较为明显。

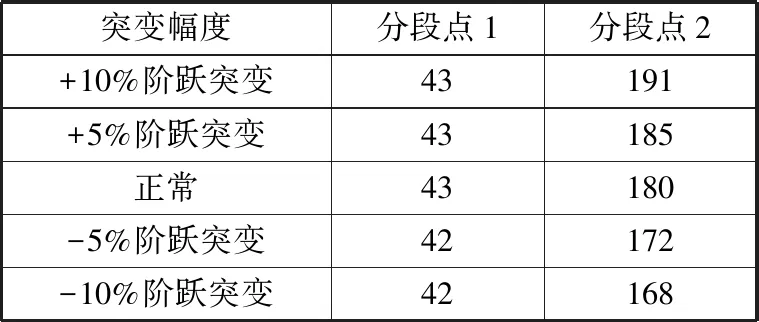
表2 基于非线性MPCA的时段划分分段点

使用基于IFRF的时段划分方法对以上数据进行时段划分，正常批次数据基于小波变换估计的IFRF展开向量强度图如图4(a)所示，KPCA降维后的特征向量强度图如图4(b)所示。

图4 IFRF向量强度图

从图4的IFRF向量强度图同样可以看出，间歇过程在100 h前存在一个明显的分段点，与基于非线性MPCA的时段划分方法具有相似的结果。将间歇过程划分为3个时段，各个突变幅度数据的时段划分结果如图5所示，时段划分的分段点如表3所示。

图5 基于IFRF的青霉素发酵过程时段划分结果

表3 基于IFRF的时段划分分段点

对表3中分段点进行统计分析，计算分段点1均值为μ1=44，标准差为σ1=0；分段点2均值为μ2=160.4，标准差为σ2=5.86。结合图5可以得出，在青霉素发酵过程的200 h～300 h底物流加速率存在不同幅度的阶跃突变时，采用基于IFRF的时段划分方法，分段点1基本不变，符合间歇过程实际情况，分段点2存在波动，集中在正常数据时段划分的分段点2周围。

计算基于非线性MPCA的时段划分方法的不同幅度突变数据分段点1和分段点2的标准差并与本文所提方法进行对比，如表4所示。

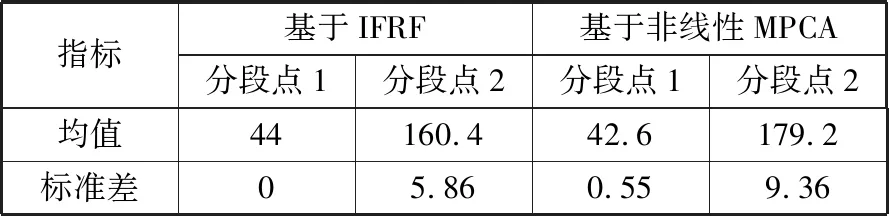
表4 分段点均值与标准差

从表2～表4可以看出，基于非线性MPCA的时段划分方法的2个分段点受输入数据突变的影响较大；本文所提基于IFRF的时段划分方法在输入数据中存在阶跃突变时，分段点1不发生变化，分段点2变化较小，具有比基于非线性MPCA的时段划分方法更小的标准差。本文所提基于IFRF的时段划分方法能够实现间歇过程的时段划分，且更加稳定，鲁棒性更强。

4 结束语

本文提出了一种基于IFRF的间歇过程时段划分方法。利用系统的动态特性不会跟随输入数据的变化而改变的特点，用描述系统瞬时动态特性的瞬时频率响应函数代替非线性MPCA方法中的过程变量数据进行时段划分。利用数值仿真过程数据和青霉素发酵过程仿真实验数据表明本文所提方法的有效性并将本文所提方法与基于非线性MPCA的时段划分进行对比实验。结果表明，所提基于IFRF的时段划分方法能够减少输入数据突变对时段划分结果的影响，具有较高的鲁棒性。