异构并行算法快速构建全球扰动重力梯度全张量图

谭勖立，王庆宾，冯进凯，黄 炎，黄子炎

信息工程大学地理空间信息学院，郑州 450001

0 引言

扰动重力位是地球重力位扣除正常椭球影响后的剩余部分，扰动重力梯度是其二阶导数，能反映变化的不规则地球产生的高频信息，可应用于大地测量[1-2]、地球物理学研究[3]、矿产资源探测[4-5]、海洋科学[6-7]和国防建设[8-9]等方面。获取扰动重力梯度的方法主要有两种[10]：一是利用高精度的重力梯度仪直接测量获得；二是根据其与其他重力场元素间的函数关系计算获得。由于西方更早开展仪器的相关研究，且针对该技术长期对国内进行封锁，国内的研制进度相对落后，暂时难以开展实测[11]，故需依靠其他重力数据资料计算获取重力梯度。可利用的资料有重力场模型[12-13]、重力异常数据[14-15]和地形数据[16]等。

在通过高阶次位系数模型计算获取大范围高分辨率的扰动重力梯度数据时，存在重复运算多、耗时长的问题。曲政豪等[12]通过交换积分次序来提高计算速度；吴星等[13]引入非正常化球谐函数，推导了广义球谐函数定积分，实现了扰动重力梯度的快速稳定计算。以上研究都从原理公式出发进行改进，但随着并行计算技术及其平台的发展，特别是以GPU+CPU为代表的异构并行计算平台的出现，使得在程序算法上的改进具有更大的可能性与潜力。例如，黄炎等[17]基于CUDA(compute unified device architecture)设计了扰动引力矢量并行计算算法算，达到了扰动引力快速计算的目的。

本文推导了扰动重力梯度张量的简化计算公式，将部分中间变量提取出来作为全局参数和局部参数，全局参数在整个计算过程中仅计算一次，局部参数也仅需在每个计算点计算一次，有效减少重复运算。在此基础上提出扰动重力梯度快速异构并行算法，利用CUDA实现梯度张量在GPU端的并行计算。根据Txx、Tyy、Tzz三个分量满足Laplace条件检验了算法可靠性，并与传统串行算法进行计算效率对比。最后，利用该算法，基于2 190阶地球重力场位系数模型EIGEN-6C4(截断至2 160阶)快速构建全球5′×5′分辨率的扰动重力梯度全张量图，并对扰动重力梯度同部分地球物理属性间的联系及其在全球范围内的数值特征进行分析。

1 基本原理

地球重力位可视为正常重力位与扰动重力位之和：

W=U+T。

(1)

式中：W为地球重力位；U为正常重力位，可由选定的正常椭球参数经过少量运算求得；T为扰动重力位，是位置的函数。在局部指北坐标系下求导可得

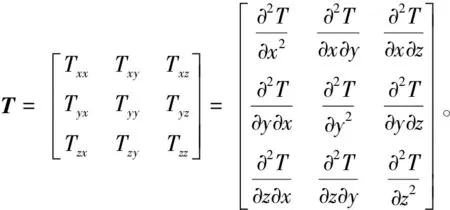
(2)

式中，函数下标x、y、z表示函数对对应坐标轴方向的偏导。矩阵中各元素为扰动重力梯度在各个方向上的分量。对于位函数，交换求导次序导数值不变，故共有6个不同分量，这6个分量构成扰动重力梯度全张量。同时，由于式(2)中矩阵对角线元素满足Laplace条件，3个元素之和为0，因此在全张量中仅有5个独立的量。

1.1 扰动重力梯度计算

扰动重力位的球谐展开式如下：

(3)

(4)

其中：

(5)

式中,各函数的具体形式可参考文献[18]中的式(21)—式(25)，由于篇幅有限本文不予展示。

1.2 计算公式简化

利用1.1节中方法大范围计算扰动重力梯度全张量时存在大量的重复计算，需对其计算方法进行必要的改进，故本文推导了计算扰动重力梯度全张量的简化计算公式。

文献[18]中的式(21)—式(25)中含有大量仅与n、m有关的项，将这些项提取出来，构成全局系数anm、bnm、cn、dnm、enm：

(6)

在计算一次后存储在内存中，之后通过n、m索引对应的数值，借此大幅减少与坐标无关项的重复计算。

在计算梯度全张量时，可将式(5)中与坐标相关但重复计算了多次的项作为局部变量，设

(7)

局部变量在每个待估点的计算过程中仅计算一次。尽可能地提取出不同项之间的公共被乘数，并将各自不相同的乘数部分相加，以进一步减少乘法运算的次数。最终，当m=0时:

(8)

当m=1时:

(9)

当m=2时:

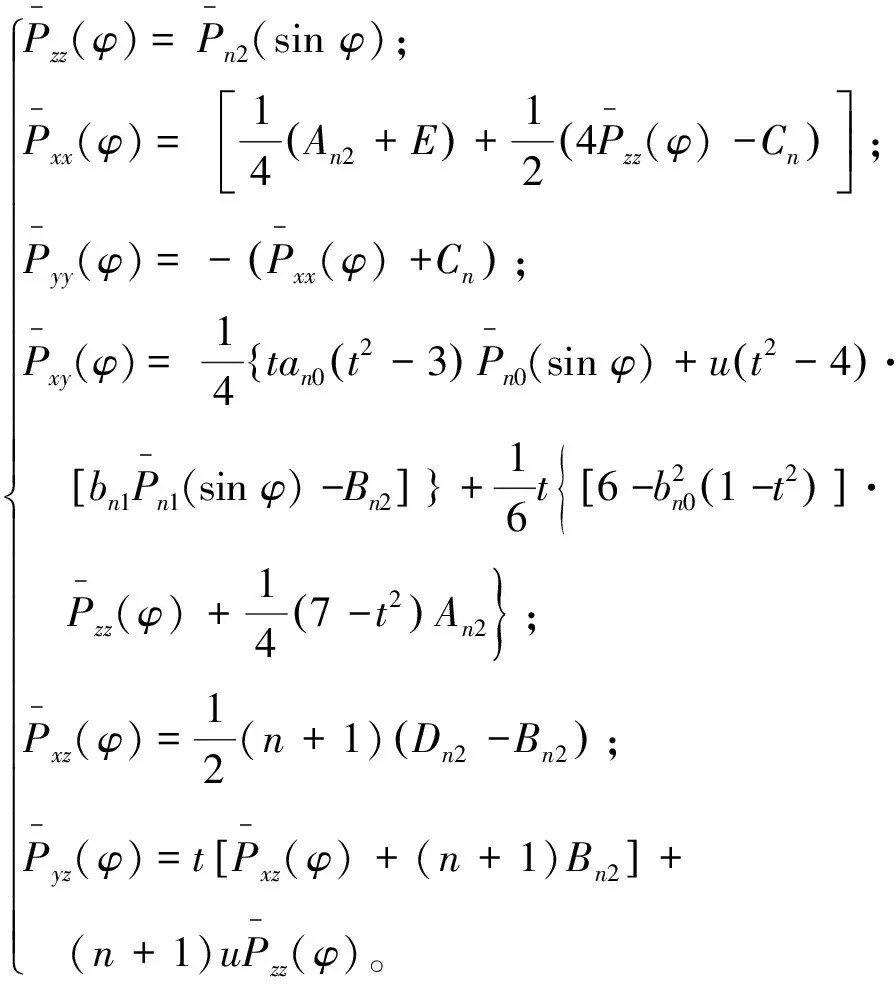
(10)

当m≥3时:

(11)

将式(6)—(11)代入式(4)中，即可获得扰动重力梯度全张量的简化计算公式。在实际编程计算时，采用交换积分次序的方法，将式(3)中三角函数的值存为中间变量，同一纬圈仅计算一次与纬度相关的量，同一经圈仅计算一次与经度相关的量。

2 异构并行算法设计

异构并行算法基于1.2节中的计算方法进行设计，利用CUDA实现GPU端的并行计算。CUDA是由英伟达(NVIDIA)推出的通用并行计算架构，可将用C、C++、FORTRAN等语言编写的程序在GPU端高性能并行执行。在设计并行算法时，需要考虑计算任务的划分粒度和运算量之间的平衡。若粒度过小，则单个任务的运算量较小，不利于发挥GPU核心的计算能力，并且会浪费过多的算力资源在线程的控制与调配上；若粒度过大，则单个任务的运算量较大，GPU核心的计算能力难以达到负载要求，同时会致使计算过程的并行化程度不高，浪费了线程资源。因此，本文算法综合考虑GPU核心的计算能力和扰动重力梯度计算过程的特点，采用分治的思想对计算任务进行递归划分[19](图1)。

第一层为待计算的扰动重力梯度格网；第二层为同纬度格网点的扰动重力梯度计算；第三层为单个格网点的扰动重力梯度计算。

在计算单个格网点的扰动重力梯度时，若计算的阶次较高，则单个GPU核心难以一次性完成计算。因此，进一步划分出更小的计算任务单元，也就是对函数fn(ρ,φ,λ)进行计算：

(12)

每个GPU仅计算其对应的fn(ρ,φ,λ)，最后将各GPU的计算结果求和，即可求得单个格网点的扰动重力梯度，即

(13)

式中，N为n的最大值，也称为最大阶数。众多GPU同时参与单个格网点的扰动重力梯度计算，可大幅减少计算耗时，进而减少整个扰动重力梯度格网的计算耗时。

3 算法可靠性与效率检验

本文基于EIGEN-6C4模型进行了扰动重力梯度的计算，计算时将模型截断至前2 160阶，利用扰动引力三分量Txx、Tyy、Tzz满足如式(14)所示Laplace条件的特性检核计算结果，并对比本文算法与传统串行算法的计算效率。

Txx+Tyy+Tzz=0。

(14)

EIGEN-6C4综合了来自LAGEOS(laser geodynamics satellite)、GRACE(gravity recovery and climate experiment)、GOCE(gravity field and steady-state ocean circulation explorer)卫星和DTU12、EGM2008、EIGEN-6C3stat模型的多源数据，最高阶次到达2 190，具有较高的精度[20]。实验计算平台为戴尔Precision 7530移动工作站，CPU为频率2.9 GHz的Intel Xeon，内存容量为32 GB，GPU为NVIDIA Quadro P3200，拥有1 792个CUDA核心。编译环境为Visual Studio 2015-Visual C++，CUDA版本10.0。

3.1 可靠性检验

利用本文算法计算了40°×60°区域内5′×5′分辨率的扰动重力梯度全张量。根据Laplace条件，即Txx、Tyy、Tzz三个分量之和为0，检核计算结果，通过求和结果相对于0值的偏差情况评判计算结果是否可靠。计算获得的三分量求和结果见表1。

由表1可以看出，扰动重力梯度三分量之和在0值附近波动，其最大值为7.816×10-13E，最小值为-9.948×10-13E，均方根为3.454×10-14E，大部分数值为10-15～10-14E。总体上三分量之和在10-12E的精度下接近于0，可认为本文算法所计算的扰动重力梯度Txx、Tyy、Tzz三个分量满足Laplace条件，算法具有较高的可靠性与准确性。

表1 三分量检核值

3.2 计算效率检验

为量化并行加速效果，引入并行加速比Sn作为参考量，其计算方式为[21]

(15)

式中：t1为串行计算所消耗的时间；tn为n个线程参与计算时消耗的时间。

分别利用本文算法与传统串行算法在Debug模式下完成如表2所示的计算任务。耗时对比结果如表3所示。由表3可见，本文算法完成各个计算任务的耗时都远低于串行算法，耗时分别缩短了91.425%、98.187%、98.444%和97.325%，并行加速比最高可达64.281。

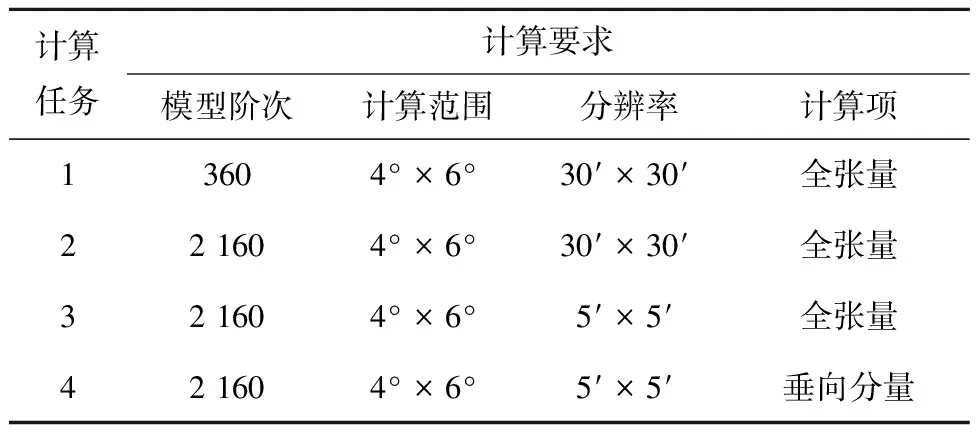
表2 计算任务

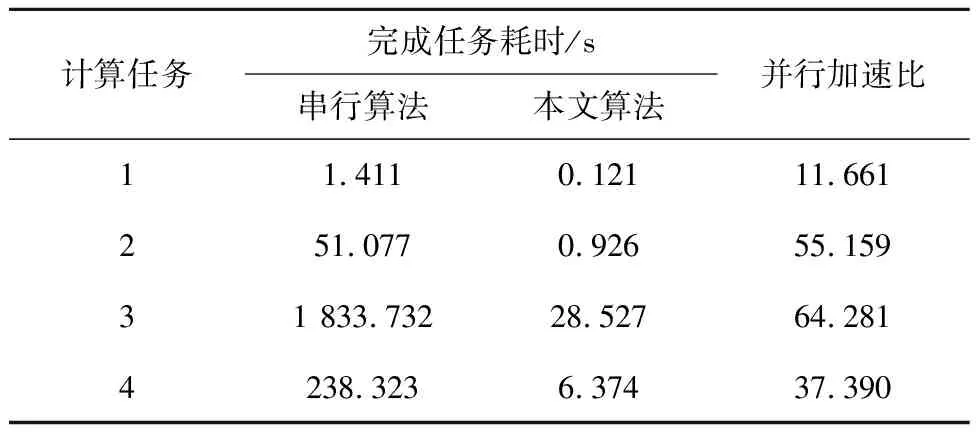
表3 算法完成任务耗时

对比本文算法完成各任务时的并行加速比可知：1)任务1由于计算量较小，此时线程分配与调度的时间占比较大，故加速效果不明显；2)由于本文采用的简化算法旨在减少大量计算梯度全张量时的重复运算，而任务4仅计算了垂向分量，因此加速比低于任务2、3；3)本文算法在采用高阶模型大量计算扰动重力梯度全张量时的加速效果最佳，且计算量越大加速效果越明显。综合来看，本文算法计算效率可达到传统串行算法的60倍以上,并且计算量越大越能凸显本文算法的优势。

4 全球扰动重力梯度全张量图构建

利用本文算法基于EIGEN-6C4模型构建了全球扰动重力梯度5′×5′分辨率的全张量图(图2)，计算了9 331 200个格网中心点，仅耗时3 h 43 min 56.326 s；而由表3推算传统串行算法需耗费时间近2月。

为便于展示和分析梯度全张量数值空间分布特征，在图2中将色标标值上下限固定为±100 E。由图2可以看出：1)梯度全张量与地形具有较高的相关性，较为清晰地反映出千岛海沟、马纳利亚海沟、四川盆地、青藏高原、柴达木盆地、埃塞俄比亚高原、东非大裂谷、大西洋中脊和安第斯山脉(图2中蓝线框住的区域)等构造特征，特别是Tzz分量，除陆地地形以外，其反映出的海底地形与文献[22]中的模型具有较高的符合度；2)环太平洋区域、喜马拉雅山脉以及东非大裂谷(图2中红线框住的区域)的梯度全张量都表现出较大的数值变化，表明这些区域质量分布变化较大，地质活动较为活跃，与全球主要的地震带与火山带的分布情况切合；3)在两极部分地区，如格林兰岛东南部海岸(图2中黑线框住的区域)，垂向分量明显大于其他分量，可认为其变化可能主要由垂向的质量损失，即冰川消融引起的，在一定程度上佐证了文献[23-25]中的发现。综合以上分析，高精度高分辨率的全球扰动重力梯度张量图在海底地形、地质变化和两极冰川等方面的研究具有一定参考意义，有助于在大尺度下把握变化规律和信息。

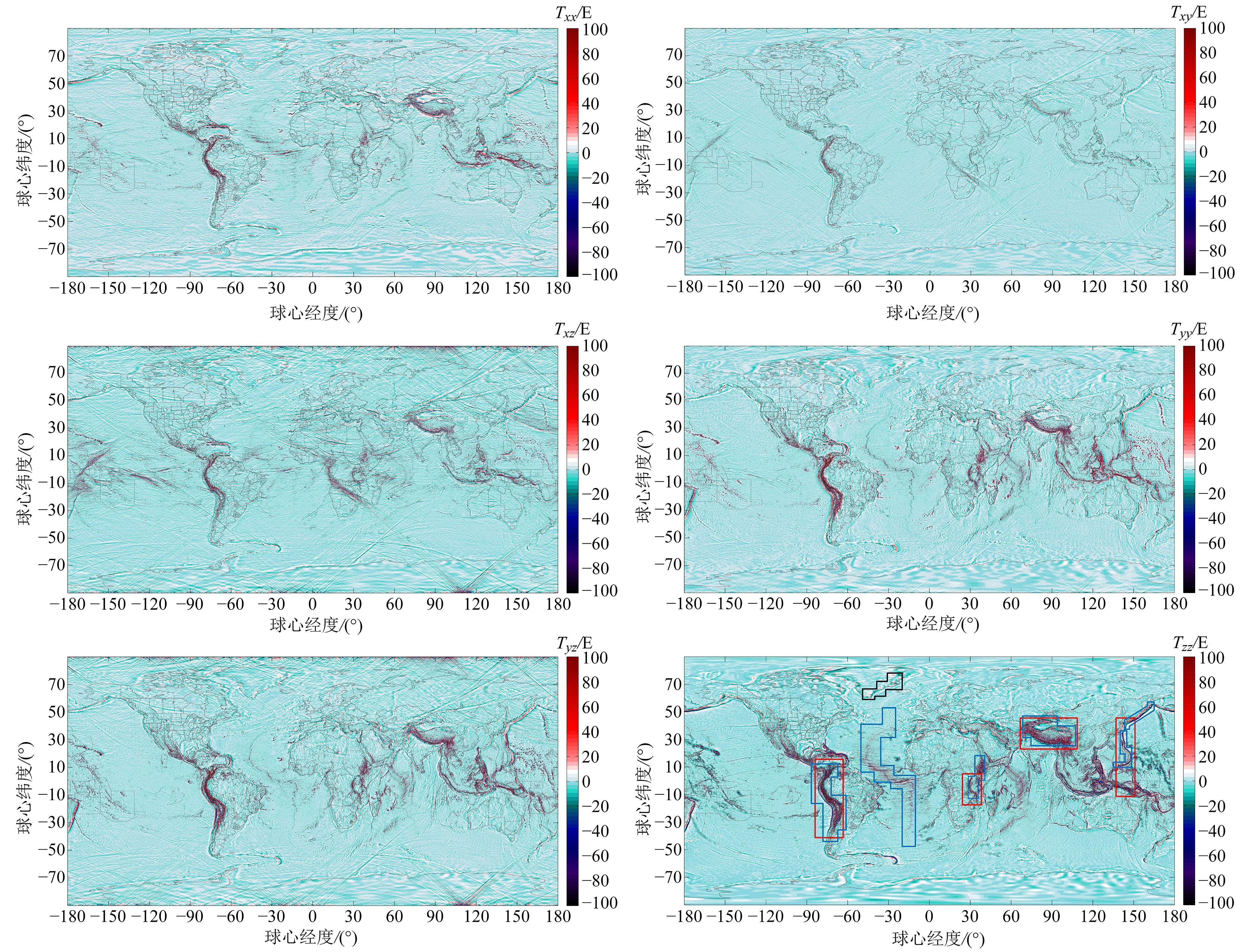
图2 全球扰动重力梯度全张量

表4反映了全球扰动重力梯度全张量的数值特征：Tzz分量数值变化范围最大，达到-557.843～785.223 E；Txy分量数值变化范围最小，仅为-138.612～149.166 E；各分量的平均值都接近于0 E，特别是Txy和Tyz分量，其均值在10-16量级上接近于0，表明扰动重力梯度的数值在全球范围内正负分布较为均匀；Tyy、Tyz、Tzz分量数值变化较为剧烈，能够较为清晰地反映扰动重力梯度的局部特征，而Txy分量数值变化较为平缓，难以反映出局部特征。

表4 全球扰动重力梯度全张量数值统计

5 结论

本文推导了扰动重力梯度张量的简化计算公式，提出了扰动重力梯度快速异构并行算法，实现了梯度全张量在GPU端的并行计算。根据Txx、Tyy、Tzz三个分量满足Laplace条件检验了算法可靠性，并与传统串行算法对比了计算效率。最后利用本文算法，基于EIGEN-6C4模型(截至2 160阶)快速构建了5′×5′分辨率的全球扰动重力梯度全张量图。得出以下结论：

1)利用本文算法计算的扰动引力三分量之和在0值附近的波动极小，振幅小于10-12，扰动引力三分量在10-12量级上满足Laplace条件，可认为计算结果准确可靠。

2)与串行算法对比，本文算法完成实验中各计算任务的耗时分别缩短了91.425%、98.187%、98.444%和97.325%，并行加速比最高达到64.281，总体上可将计算效率提高60倍以上，算法快速高效。

3)全球扰动重力梯度全张量的计算结果显示梯度全张量与地形具有较高的相关性，且能在一定程度上反映出局部区域质量分布变化情况。在数值分布方面，不同分量表现出不同的特征，Tzz分量数值变化范围最大，Txy分量则最小；Tyy、Tyz、Tzz分量数值变化较为剧烈，Txy分量数值变化则较为平缓；各分量的平均值都接近于0 E。

综合以上分析，本文算法能有效改善高阶模型计算扰动重力梯度张量时效率低下的情况，可为获取全球高分辨率扰动重力梯度数据提供高效可靠的实施方案；利用本文算法快速构建的全球扰动重力梯度全张量图可以了解掌握各分量在全球范围内的数值分布情况，对海洋地形、地质变化和两极冰川相关研究也具有一定的参考意义。