基于环绕测点子区分割的数字图像相关方法剪切带宽度测量研究
张博闻, 王学滨,2, 董 伟
(1.辽宁工程技术大学 力学与工程学院,辽宁 阜新 123000;2.辽宁工程技术大学 计算力学研究所,辽宁 阜新 123000)
1 引 言
剪切带是狭窄的具有高应变梯度的带状区域,是材料破坏的一种重要前兆。剪切带几乎可以在各种材料破坏过程中被观测到,例如,岩土、金属、陶瓷、复合材料和合金等。对剪切带的研究可以深化了解材料的破坏过程,有助于揭示材料变形破坏机理。目前,数字图像相关(digital image correlation,DIC)方法已成为剪切带研究的最经济有效的方法[1~4]。剪切带宽度是剪切带的重要特征之一,其准确测量一直得到密切关注。Nübel K[5]利用高斯拟合方法测量了剪切带宽度,认为剪切带宽度是正态分布标准偏差的2倍。王学滨等[6]提出了基于背景值方法的剪切带宽度测量方法,对黏土的剪切带宽度随纵向应变的演化演变规律进行了测量,并认为Nübel的高斯拟合方法不能准确测量含应变梯度的虚拟剪切带和真实剪切带的宽度。事实上,无论采用何种剪切带宽度测量方法,要得到比较准确的剪切带宽度,其根本在于准确测量剪切带边界附近的应变。在利用DIC方法测量剪切带的应变时会存在较大的误差,为此,学者们对DIC方法进行了各种修正[7~11]。其中,有代表性的方法是Poissant J等[10]提出的子区分割方法。在该方法中,利用对非连续变形位置线性拟合出的分割线将样本子区分割为主、副2个子代子区,以主子区的位移和应变作为结果,从而改善了裂纹附近的结果,但对剪切带边界附近的应变计算误差较大。为此,杜亚志等[11]提出了一种修正的子区分割方法。在该方法中,利用过子区中心点且倾角为剪切带倾角的分割线将子区分割成2个子代子区,将相关性好的子代子区的位移作为结果,从而改善了剪切带附近位移的结果。但是,在多条剪切带相交区域,由于准确测量剪切带倾角较为困难,从而难以确定该方法的子区分割线。这2种方法的实质都是将子区分割成不同形状的区域,计算过程相对较复杂。
本文提出了环绕测点子区分割一阶DIC方法,以提高剪切带应变测量精度,通过虚拟剪切带宽度测量验证了提出方法的有效性。在剪切带宽度测量中,将基于本文方法的结果与基于粒子群优化和Newton-Raphson迭代的粗-细方法的结果进行了对比,并从理论上分析了剪切带宽度的测量误差。
2 环绕测点子区分割一阶DIC方法
2.1 DIC方法的基本原理
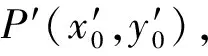
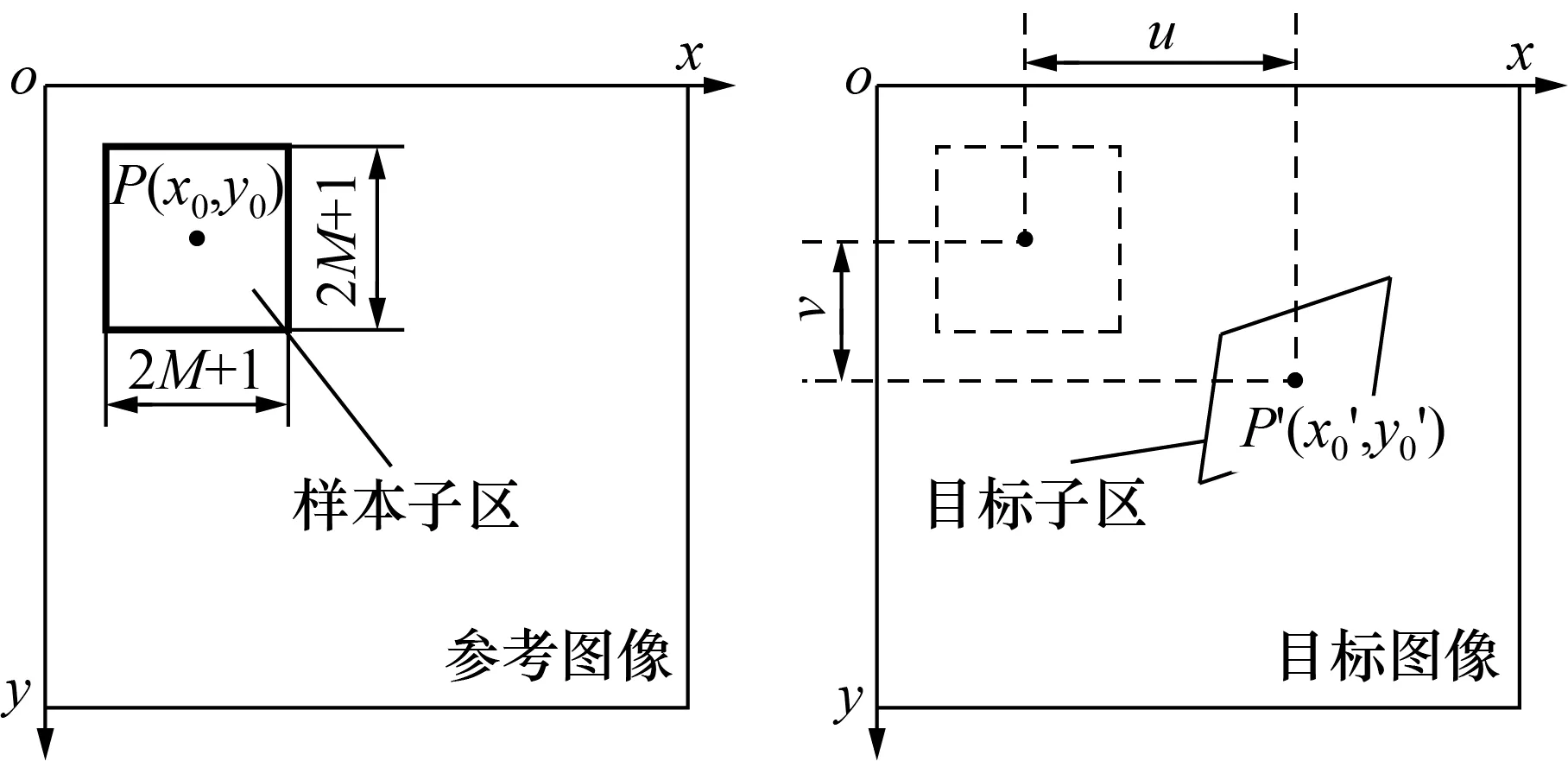
图1 DIC方法的基本原理
样本子区与目标子区的相关性用相关函数来表示。零均值归一化互相关函数CZNCC对图像灰度的波动和线性变化不敏感,被广泛使用[12]。CZNCC可以表示为:
(1)
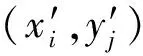
子区内任意一点的位移表达式称为形函数(或位移模式),常用的一阶形函数为:
(2)
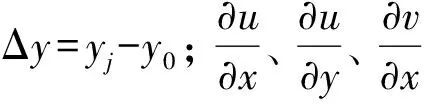
在传统DIC方法中,当测点远离剪切带时,一阶形函数可以较准确描述子区变形。但是,当测点位于剪切带边界附近时,由于剪切带内、外的变形差异较大,子区可能覆盖两种及以上的变形,从而影响计算精度。
2.2 环绕测点子区分割一阶DIC方法
鉴于传统DIC方法在剪切带边界附近测量精度较低和现有子区分割方法分割线不易确定的缺点[10~11],本文提出了环绕测点子区分割一阶DIC方法(改进子区分割方法)。该方法的基本原理是通过对选定测点(相关性不好)的原始子区进行有限分割,保证后代子区环绕在测点周围,使一些后代子区位于简单变形区域,从而可以搜索到较好结果,并将其中的最佳结果作为选中测点的结果。其具体流程图如图2所示。
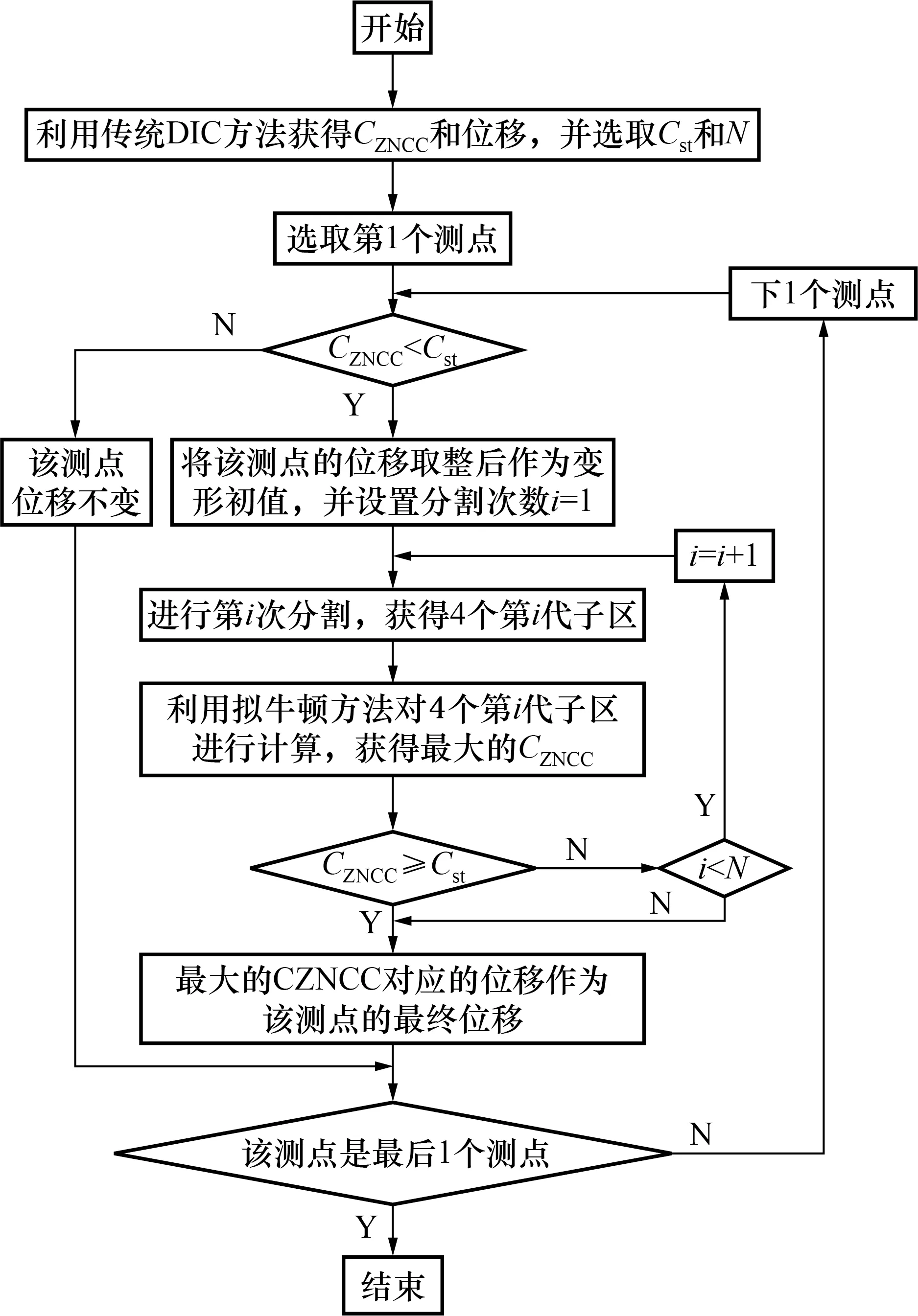
图2 改进子区分割方法的计算流程图
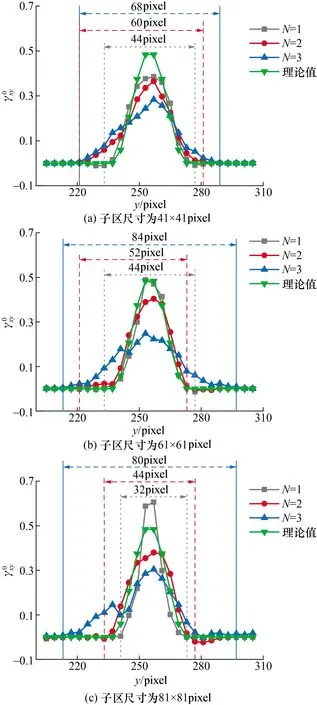
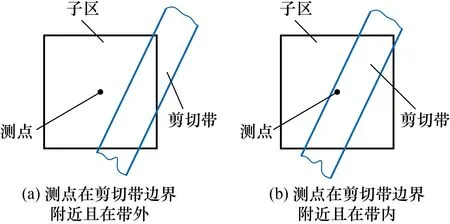
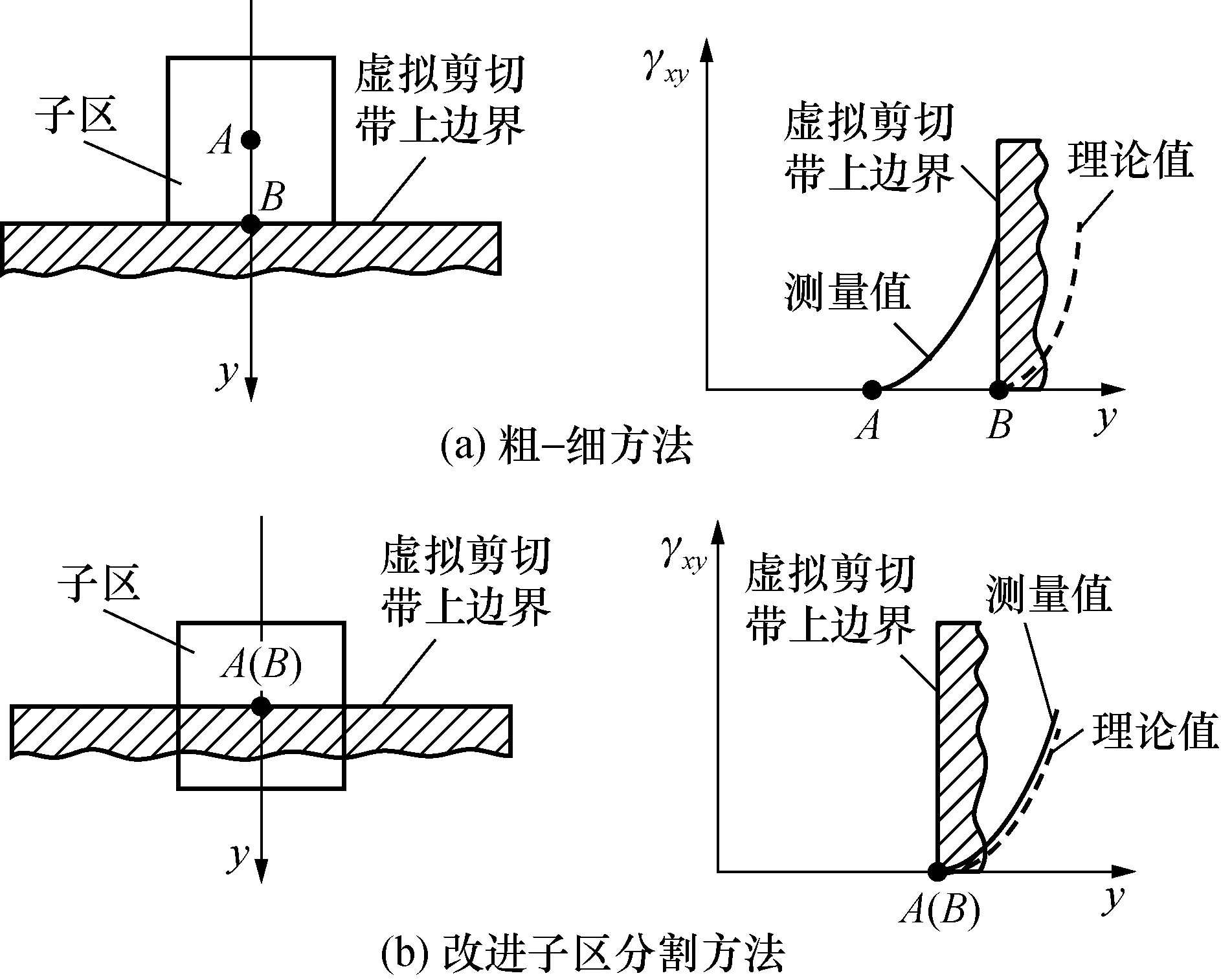
1)确定第0代子区。在传统DIC方法中,剪切带边界附近及带内测点的CZNCC较小(相关性不好)。因此,根据CZNCC的总体分布和子区尺寸,选取合适的阈值Cst。若CZNCC 2)分割子区并计算下一代子区的位移。将子区的水平和垂直对称线作为子区分割线,将第0代子区分割为4个第1代的后代子区,将选中测点的位移取整后作为变形初值,利用拟牛顿方法重新计算位移。一旦满足CZNCC≥Cst,则将最大CZNCC对应的位移作为选中测点的最终位移。否则,对后代子区继续分割,选择分割后子区中包含测点的4个,以构造第2代后代子区,计算并进行上述比较,以此类推。若始终没有满足上述条件,则将最终子区中最大CZNCC对应的位移作为选中测点的最终位移。应当指出,代数越大,后代子区的尺寸越小;选取的最大分割次数N不应太大,否则,分割后的子区包含的灰度信息会过少,导致相关搜索困难。经验表明,最终子区尺寸应大于3×3像素。此外,在分割后,各代子区拥有共同的中心点,这可以确保选中测点所在行、列的灰度信息参与各代子区的计算。 3)对于下一个测点,若CZNCC 根据Zhou方法[11]制作模拟散斑图(图3(a)),其尺寸为256×512pixel,散斑数量为5 000,散斑半径为3pixel,并建立如图3所示的直角坐标系。以图3(a)为参考图像,根据塑性梯度理论[13],利用仿射变换技术制作含应变梯度的水平虚拟剪切带的图像(图3(b))。 图3 参考图像与含水平虚拟剪切带的图像 在剪切带外,塑性剪切应变γP(y)≡0;在剪切带内,其理论值为: (3) 在制作剪切带的过程中,只允许剪切带发生简单剪切变形。此外,由于剪切带内只有塑性剪切应变,而无弹性剪切应变,所以,面内剪切应变γxy的理论值可以表示为: γxy=γP(y) (4) 选取基于粒子群优化和Newton-Raphson迭代的粗-细方法(粗-细方法)与改进子区分割方法进行对比,分别计算图3(a)变形至图3(b)时的位移,计算区域如图3(a)所示。在计算时,子区尺寸和测点间隔是粗-细方法和改进子区分割方法共有的计算参数,Cst和N为后者独有的计算参数。由于最小一乘拟合方法[14]可以较好抑制计算窗口内“异常值”的影响,从而可以较准确获得剪切带边界附近的非均匀应变。因此,本文利用最小一乘拟合方法分别获得γxy,其中,拟合窗口尺寸为5×5个测点。由于剪切带外的γxy理论值为0,因此剪切带实测宽度w应该为测线上γxy>0区域的宽度。考虑到应变测量的误差[15],将γxy>0.001的区域认为是剪切带区域。 图4 不同子区尺寸时2种方法的分布 由图4可以发现,随着子区尺寸的增加,粗-细方法的w逐渐变大;改进子区分割法的w变化不大,比粗-细法的更接近w0。当子区尺寸由31×31pixel增加到61×61pixel时,粗-细方法的w的相对误差分别为66.7%、88.9%、111.1%和133.3%,而改进子区分割方法的分别为11.1%、22.2%、0.0%和22.2%。由此可见,子区尺寸对粗-细方法的w影响较大,而对改进子区分割方法的影响较小。为了研究测点间隔对w的影响,分别选择测点间隔为2和3pixel,子区尺寸为61×61pixel,Cst=0.999,N=1进行计算。 图5 不同测点间隔时两种方法的分布 图6 不同Cst时改进子区分割方法的分布 由图6可以发现,随着Cst的增加,改进子区分割方法的w变化不大,当Cst分别为0.9、0.99和0.999 9时,改进子区分割方法的w均为44pixel,w的相对误差均为22.2%。由此可见,Cst对w的影响可以忽略不计。 图7 不同N及子区尺寸时改进子区分割方法的分布 由图7可以发现,当子区尺寸确定时,随着N的增加,改进子区分割方法的w逐渐变大;当子区尺寸较大时,与子区较小时的情况相比,较大N的结果更精确。例如,当子区尺寸为41×41pixel时,N=1、2和3时的w分别为44、60和68pixel,w的相对误差分别为22.2%、66.7%和88.9%,显然,N=1时的最接近理论值;当子区尺寸为61×61pixel时,N=1、2和3时的w分别为44、52和84pixel,w的相对误差分别为22.2%、44.4%和133.3%,显然,N=1时的最接近理论值;当子区尺寸为81×81pixel时,N=1、2 和3时的w分别为32、44和80pixel,w的相对误差分别为-11.1%、22.2%和122.2%,显然,N=1时的w相对误差限最小且w误差为负,而理论上使用DIC方法和最小一乘拟合方法会高估剪切带宽度(具体分析见第4节),w误差不应小于0,所以,N=2时的w更精确。综上所述,N对w的影响较大,当子区尺寸适中时,例如,当子区尺寸为41×41或61×61pixel时,选择N=1即可;当子区尺寸较大时,例如,当子区尺寸为81×81pixel时,选择N=2即可。 剪切带一般较窄,而子区尺寸一般为几十pixel。所以,通常剪切带宽度小于子区尺寸。当测点在剪切带边界附近时,子区会包含剪切带和带外区域。对于下列情形,即测点在剪切带外(图8(a))和测点在剪切带内(图8(b)),分别进行讨论。对于测点在剪切带外的情形,和带内的γxy相比,测点的本应较低。对于测点在剪切带内的情形,和带外的γxy相比,测点的本应较高。但是,在测量时,测点的γxy是子区的γxy的平均效果。对于测点在剪切带外的情形,测点的γxy将被高估,而对于测点在剪切带内的情形,测点的γxy将被低估。 图8 测点与剪切带的相对位置 设子区尺寸为(2M+1)×(2M+1)pixel,以剪切带上边界附近的子区为例进行分析。设子区中心点为A,过点A垂直于剪切带建立y轴,向下为正,y轴与剪切带上边界交于B点(图9)。 对于粗-细方法,当点A距离剪切带上边界的距离为M时,由于点A的子区全部在剪切带外,所以,有γxy=0(图9(a))。当上述距离小于M时,由于子区包含部分剪切带,所以,有γxy≠0。因此,图9(a)的情形应为一种临界情形。此时,w将被高估至w0与2M之和,即由子区尺寸引入的剪切带实测宽度理论误差wt为2M。 图9 子区尺寸对w影响示意图 对于改进子区分割方法,当点A在剪切带上边界上时,点A的1个后代子区在剪切带外总存在,所以,有γxy=0(图9(a))。因此,w与w0相等,由子区尺寸引入的wt为0,这充分体现了改进子区分割方法的优势。 应当指出,当有两个测点恰巧被分别布置在点A(图9(a))和点B(图9(b))时,测点间隔引入的wt为0。实际上,除了测点间隔为1pixel时之外,上述情形不容易出现。所以,通常w将被高估。测点间隔不应过大,以增加测点距离剪切带边界更近的可能性,从而减小由测点间隔引入的wt。 设最小一乘拟合窗口尺寸为(2K+1)×(2K+1)个测点,以剪切带上边界附近的子区为例进行分析(图10)。设最小一乘拟合窗口中心点为C,过点C垂直于剪切带建立y轴,向下为正。y轴分别交拟合窗口下边界和剪切带上边界于点D、E(图9(a))。应当指出,图10(b)中点D、E重合。 图10 最小一乘拟合窗口对w影响示意图 对于改进子区分割方法,当点D在剪切带上边界上时,点C的γxy=0(图10(b)),此时,剪切带宽度将被高估值至理论宽度与2K×测点间隔之和,即最小一乘拟合方法引入的wt为2K×测点间隔。 由第4.2节和4.3节可知,DIC方法和最小一乘拟合方法都会引入wt。这里,将修正后剪切带实测宽度w1定义为w与wt之差;通过对比两种方法的w1,以进一步验证改进子区分割方法的优势。对于测点间隔为4pixel、最小一乘拟合窗口为5×5个测点的情形,此时,剪切带的上、下边界上恰好被布置了测点。根据第4.2节和第4.3节,由改进子区分割方法和最小一乘拟合方法引入的wt分别为0和16pixel,即wt为16pixel。 表1给出了不同子区尺寸时2种方法的wt、w和w1。由此可以发现,粗-细方法的w1与w0相差较大,而子区分割方法的w1更接近w0,这表明改进子区分割方法更适于剪切带宽度测量。例如,当子区尺寸分别为31×31、41×41、51×51和61×61pixel时,粗-细方法的w1与w0相差分别为-22、-24、-26和-28pixel,而修正后改进子区分割方法的分别为-12、-8、-16和-8pixel。 表1 不同子区尺寸时2种方法的wt、w和w1 对于狭窄且具有高度应变梯度的剪切带,传统数字图像相关方法很难精确测量其宽度,提出了一种环绕测点子区分割数字图像相关方法,通过对制作的虚拟剪切带进行宽度测量验证了提出方法的有效性。基于粒子群优化和Newton-Raphson迭代的粗-细方法的剪切带宽度误差与子区尺寸密切相关,其剪切带宽度理论误差接近子区尺寸,而环绕测点子区分割方法的剪切带宽度理论上不受子区尺寸的影响。对于环绕测点子区分割方法,其最大子区分割次数依赖于测点的原始子区尺寸,常用的子区尺寸分割1次即可获得较好结果;测点分割相关系数阈值的影响微乎其微;但测点间隔不应过大,以减小测量误差。3 虚拟剪切带的制作及宽度测量
3.1 虚拟剪切带的制作

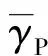
3.2 虚拟剪切带宽度测量
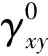
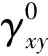
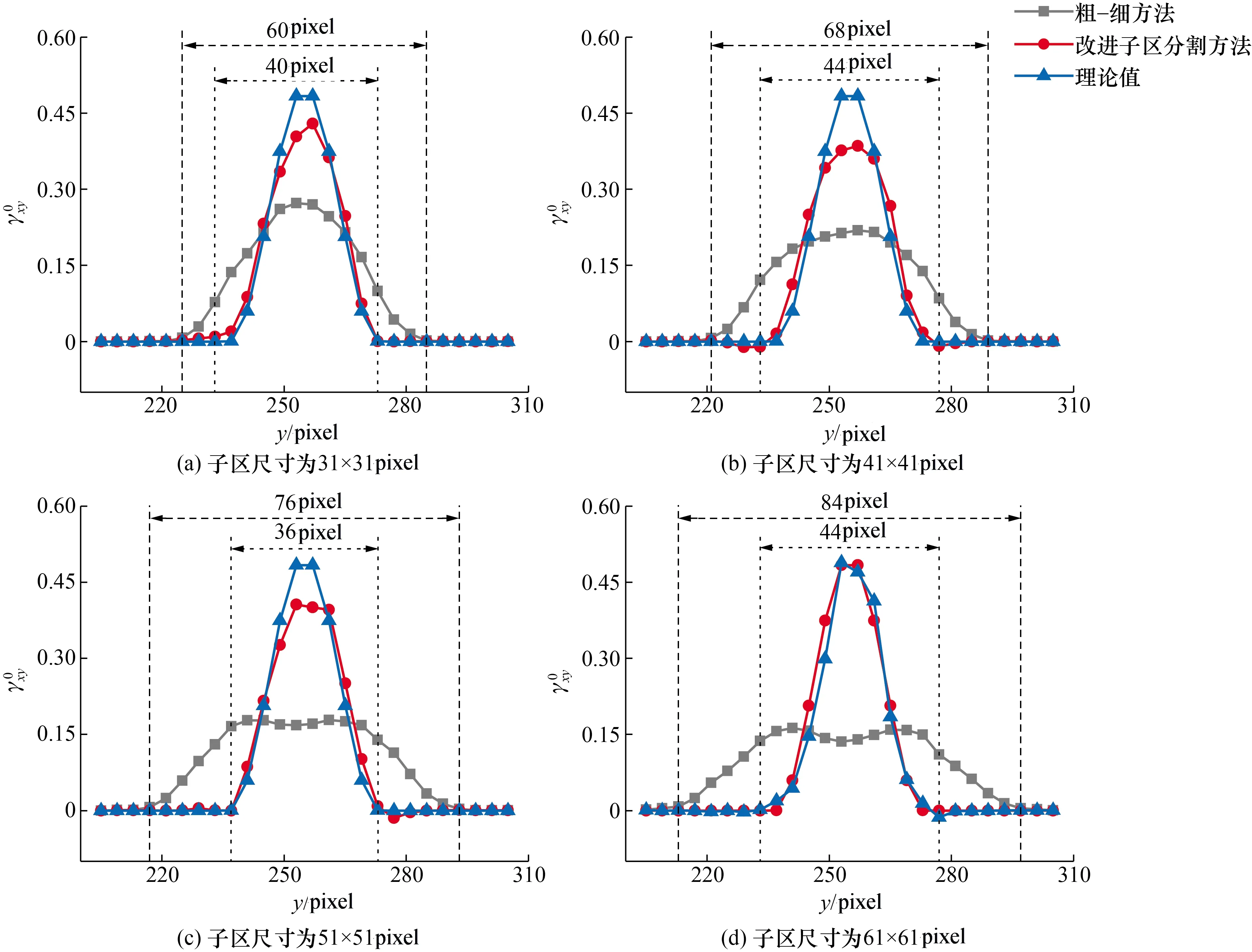
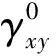
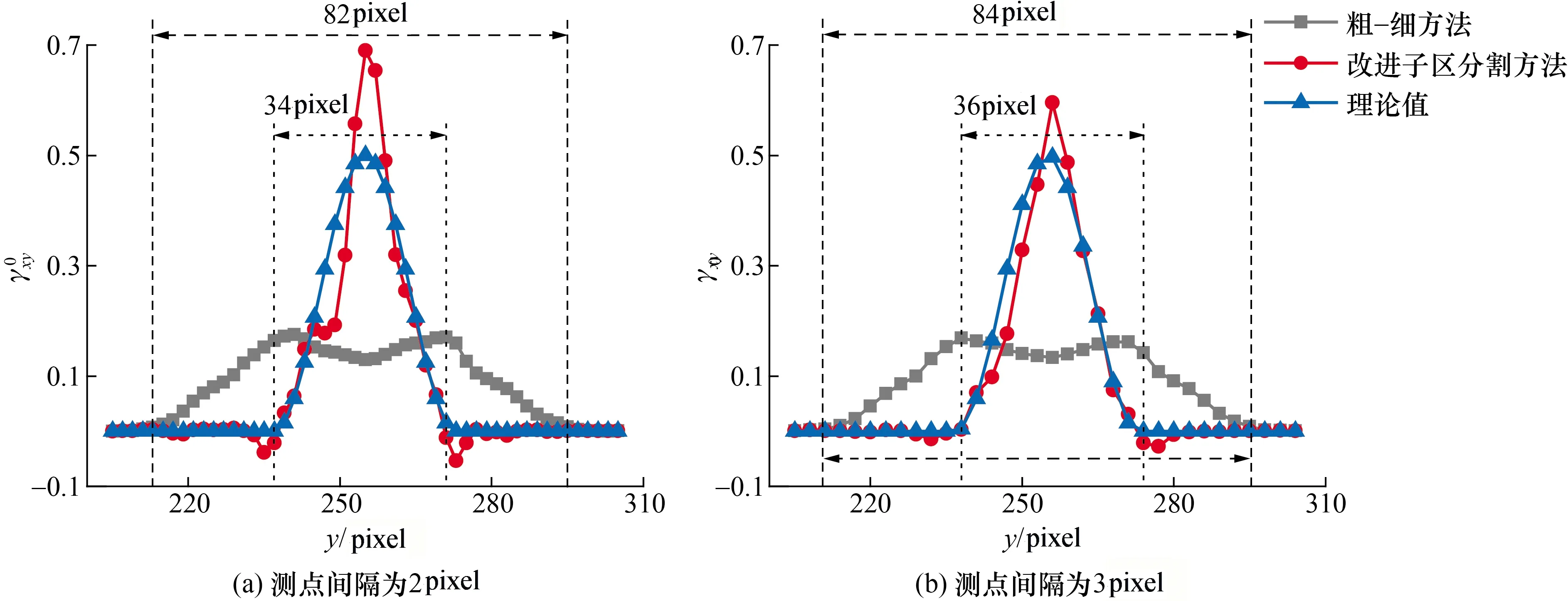

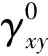
4 剪切带实测宽度理论误差分析
4.1 测点不同位置时粗-细方法的剪切带实测宽度理论误差分析
4.2 不同子区尺寸及测点间隔时的剪切带实测宽度理论误差分析
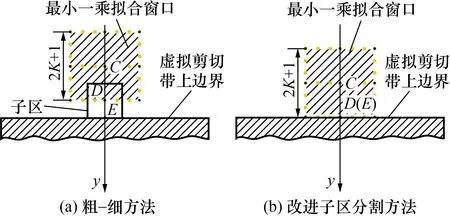
4.3 最小一乘拟合方法引入的剪切带实测宽度理论误差分析
4.4 w的修正及检验

5 结 论

