1 on 1损伤阈值测量结果不确定度分析

巴荣声， 李 杰， 周信达， 郑垠波， 徐宏磊，丁 磊， 李亚军， 那 进

(中国工程物理研究院 激光聚变研究中心，四川 绵阳 621900)

1 引 言

光学表面抗激光损伤性能是制约高功率激光器输出能力的瓶颈[1]。根据光学表面实际应用场景，评价光学表面激光诱导损伤阈值的方法主要包括 1 on 1、S on 1、R on 1等[2]。在标准ISO 11254、ISO 21254(国内等效标准GB/T 16601)中，明确了1 on 1、S on 1损伤阈值测试方法及结果测量不确定度分析方法，国内相关研究人员也开展了相关分析评定工作[3～5]。

ISO 21254推荐的1 on 1测试方法以激光在光学表面的能量密度表征激光辐照量，要求在测试样品上每个测试点只进行一次激光辐照，对于每个选定的脉冲能量至少选取10个测试点，分别计算不同脉冲能量辐照下损伤概率，拟合损伤概率-激光辐照量的关系曲线，获得损伤几率为零的最大激光辐照量，定义为光学元件损伤阈值或零概率损伤阈值。

采用1 on 1测试方法进行光学元件损伤阈值测试，影响测量结果不确定度的主要因素包括：

(1)激光脉冲能量测量引入的不确定度，主要来源于分光系数、能量台阶内激光脉冲能量波动及激光能量计；

(2)光斑面积测量引入的不确定度，主要来源于光斑面积测量装置、光斑面积波动、光斑有效区域确定方法；

(3)线性拟合引入的测量不确定度，主要来源于能量密度、损伤概率以及测试能量台阶数目。

在上述测量不确定度影响因素中，线性拟合引入的测量不确定度评定比激光脉冲能量及光斑面积测量引入的测量不确定度更复杂。为了降低零概率损伤阈值的测量不确定度，一般使用最小二乘法对待拟合实验数据进行拟合，获得最佳拟合参量。在最小二乘法直线拟合过程中，不同的残差模型影响计算结果，当残差模型较为复杂时，难以采用公式方法给出结果不确定度。

本文围绕1 on 1损伤阈值测量结果的不确定度，采用公式法分析评定能量密度、损伤概率的测量不确定度分量；针对损伤概率与能量密度的线性拟合，采用蒙特卡洛方法分析对比不同残差模型对线性拟合结果的影响规律，综合评定光学表面1 on 1损伤阈值测量结果的不确定度。

2 ISO 21254阈值测量不确定度评定方法讨论

ISO 21254推荐的损伤测试原理框图如图1所示。

图1 激光损伤测试原理框图

其测试原理为激光系统出射激光由会聚系统聚焦至样品室内样品光学表面，达到能量密度提升、引发光学表面损伤的目的。固定激光脉冲能量，采用随机抽样的方式对在该能量密度下表面是否发生损伤进行测试，在线损伤探测器通过对比光学表面激光辐照前后变化，确定该能量密度下表面是否发生损伤。每个测试点仅辐照1次，观察损伤与否后移动样品，开始下1个测试点的测试，直至在该能量下测试点数目满足要求。更改激光脉冲能量，重复上述步骤，直至损伤概率测试结果满足要求。

可变衰减器与波片的作用是调节激光脉冲到达样片表面能量密度及偏振态，获得相同偏振态、不同能量的激光脉冲。分光镜的作用是对主激光束进行固定分光比分束，分束后低能量光束进入光束诊断装置，由该装置给出激光脉冲空间分布、时间分布、分光能量等光束信息。

ISO 21254附录A中提供了损伤概率、损伤阈值以及其不确定度的计算方法。在附录A.4中，单能量段损伤概率Pi计算公式如式(1)所示，损伤概率测量不确定度如式(2)、式(3)所示。

(1)

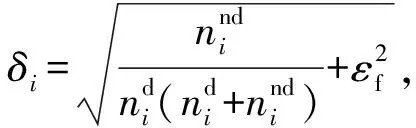
(2)

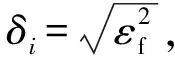
(3)

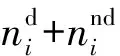
将损伤概率测量不确定度的倒数作为权重(1/δi)，采用加权线性拟合的方式，对能量密度H、损伤概率P进行线性拟合，获得二者函数关系，式(4)～式(6)是ISO 21254给出的拟合直线斜率M和截距b计算公式(为本文表述一致，将该标准中的直线拟合斜率符号m更改为M)。

(4)

(5)

(6)

“零”概率损伤阈值计算公式如式(7)所示，式(8)～式(10)是ISO 21254中提供的零概率损伤阈值测量结果不确定度评定公式。

(7)

(8)

(9)

(10)

ISO 21254对于损伤阈值测量不确定度评定主要存在以下几个方面的问题。

a)损伤概率P测量不确定度连续性问题

损伤概率测量不确定度的这种不连续性将导致有限抽样测试条件下，无损伤点的损伤概率测试结果在拟合过程中权重被过分的放大，按式(4)～式(6)进行加权拟合计算阈值时，阈值拟合结果偏大，示意图如图2所示。

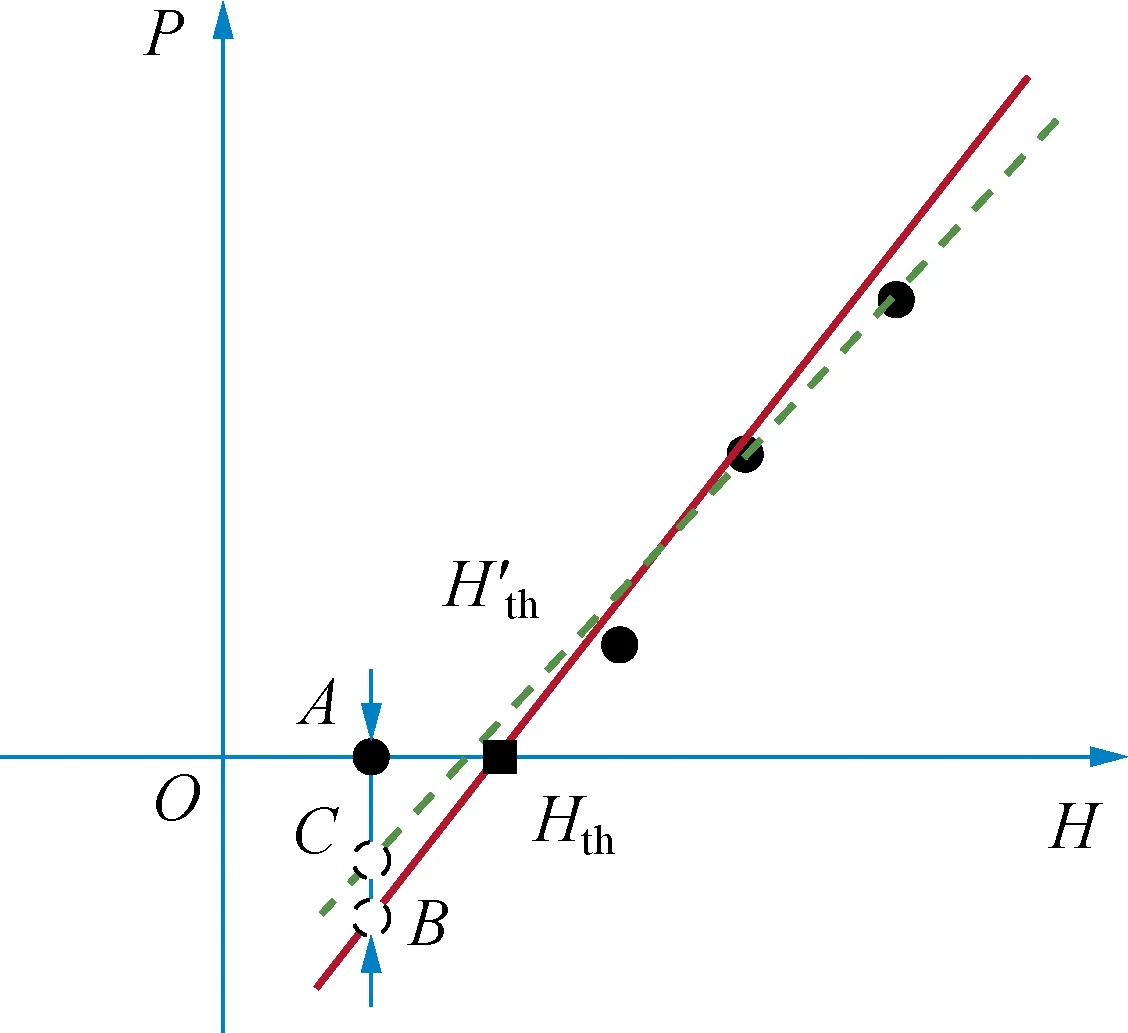
图2 阈值拟合过程示意图

b)损伤概率测量不确定度评定合成问题

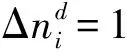
(11)

若认为损伤概率与能量密度独立不相关，应按平方关系进行合成，而式(2)直接以偏差代替损伤概率不确定度的平方，导致损伤概率测量不确定度评定存在问题。

c)损伤阈值测量不确定度评定合成问题

损伤阈值测量不确定合成式(8)成立的条件是斜率M与截距b独立不相关。

采用极大似然法求解M与b过程中，2个参数求偏导后联立成方程组，2个方程是相关的，不是独立的，式(6)的另一种表述如式(12)所示。

(12)

因此，在损伤阈值不确定度合成过程中，需要计算M与b的相关系数，并按不确定度相关合成方法进行计算[6](M、b相关系数实例计算结果见表5模拟结果)，而ISO 212154附录中直接按M与b独立不相关处理损伤阈值不确定度是不正确的。

针对上述问题，本文采用公式法分析评定能量密度、损伤概率的测量不确定度，采用蒙特卡洛方法评定光学表面1 on 1损伤阈值测量不确定度。

3 损伤阈值蒙特卡洛法测量不确定度分析

3.1 线性拟合最小二乘法残差模型

假定变量P、H满足式(13)所示线性关系，待拟合系数分别为a0、a1。

P=a1H+a0

(13)

均权最小二乘法求解系数a0、a1过程中，常见的不同残差模型其回归系数计算方法如表1所示[7～10]。

表1 残差模型与回归系数

表1中，第1个残差模型认为H无误差，仅考虑P的误差(Ⅰ型)。第2个残差模型认为P无误差，仅考虑H的误差(Ⅱ型)。第3个残差模型下，拟合直线在H方向与P方向的误差同时达到最小(Ⅲ型)。第四个残差模型为测试数据点到拟合直线的距离残差最小(Ⅳ型)。其中Ⅲ型、Ⅳ型残差模型涉及到一元四次方程和一元二次方程，需要数值求解或开方求解，表中仅给出了a0、a1的表达式。

3.2 能量测量结果不确定度评定

根据ISO 21254推荐的测试光路(图1)开展损伤阈值测试时，设到达测试样品表面激光脉冲能量为Q1，光束诊断装置中采集的激光脉冲分光能量为Q2，二者比值为分光系数N。分光系数在测量主激光能量Q1过程中涉及到激光能量Q2，二者是相关的，为了去除这种相关性，需要在阈值测量前独立标定分光系数，使之作为独立测量参量参与能量测量结果的测量不确定度合成。

(14)

(15)

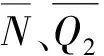
设uNA为分光系数A类不确定度，uNB为分光系数B类不确定度(激光能量计不确定度)，则分光系数不确定度分量uN如式(16)所示。

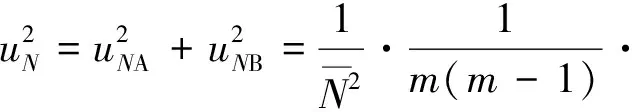
(16)

式中，uQ1B、uQ2B分别表示激光能量计B类测量不确定度(单位为“%”，k为包含因子)。

样品表面能量测量结果Q1的相对不确定度uQ1如式(17)所示。

(17)

式中uQ2表示激光能量Q2的相对不确定度。

3.3 光斑面积测量结果不确定度评定

影响光斑面积测量结果的因素包括：

1)共轭聚焦系统共轭距离偏差引入的相对不确定度uS1；

2)科学级CCD面响应非均匀性引入的相对不确定度uS2、响应线性拟合对引入的相对不确定度uS3；

3)不同激光脉冲能量下，光斑面积波动引入的相对不确定度uS4；

4)光斑有效区域确定方法引入的相对不确定度uS5。

近似认为影响光斑面积测量结果的不确定度分量独立不相关条件下，光斑面积测量结果的相对不确定度uS如式(18)所示。

(18)

共轭测量样品表面平顶光斑空间分布时，设激光脉冲进入聚焦系统前等效光斑半径为R，聚焦后样品表面等效光斑半径为r，样品表面光斑面积为S，聚焦系统等效焦距为F，样品与聚焦点距离为z，光斑大小变换采用几何光学处理时，光斑面积及相对不确定度如式(19)、式(20)所示。

(19)

(20)

能量测量不确定度一般大于1%，若Δz/z远小于1%(如Δz=10mm，z=1 600mm)，则在计算能量密度测量不确定度时可忽略由于光斑面积共轭测量过程中距离偏差引起测量不确定度uS1。

此外，科学级CCD的面响应非均匀性约2%，能量响应线性拟合度大于98%，对于像素数大于 1 024×1 024像素的面阵CCD而言，当样品表面的光斑分布为平顶光斑时，单像素点的响应均匀性以及能量响应引起的测量不确定度远小于1%，故可忽略CCD面响应均匀性、能量响应线性拟合度引起的测量不确定度uS2、uS3。

(21)

(22)

(23)

式中:下标i表示第i次测量。

不同光斑边缘确定方法将导致同一光斑面积计算出现差异，但该差异属于光斑确定方法定义引起的，因此不包含在光斑面积的重复测量结果(A类)不确定度uS4内。uS中uS4是由于激光脉冲能量波动引起，uS5是由光斑区域确定方式引起，二者是独立的，即相同激光能量下，光斑区域确定方式不同引起的面积测量结果不同与对应的激光能量无关。

3.4 能量密度测量结果不确定度评定

使用式(24)计算单能量台阶内的能量密度H时，能量密度相对标准测量不确定度uH如式(25)所示。

(24)

(25)

式中:uQ1表示脉冲能量Q1相对不确定度分量;uS表示光斑面积S相对不确定度分量。从式(25)可以看出，采用相对不确定度对能量密度不确定度评定过程中，能量密度测量不确定度主要受能量测量不确定度及面积测量不确定度影响。

3.5 损伤概率测量结果不确定度评定

损伤概率测量不确定度对应的是某一能量密度光学表面损伤概率与损伤概率“真值”差值范围，在无法获得真值的情况下，本文以均权拟合直线残差作为损伤概率的测量不确定度。

设能量密度Hi对应损伤概率Pi，能量密度与损伤概率关系曲线为 f(H)，则损伤概率的测量不确定度uP如式(26)所示。

(26)

式中:m表示能量台阶总个数;i表示能量台阶序数。

3.6 损伤阈值测量结果不确定度评定

根据中心极限定理，当样本数足够大时，平均值的概率分布为正态分布[11]，本文假定光学表面损伤阈值实测参数(能量、面积、损伤概率)平均值服从正态分布，对损伤阈值测量结果进行了蒙特卡洛模拟[12～16]。模拟使用的某次光学表面损伤阈值参数测量结果数据(k=1)如表2所示。

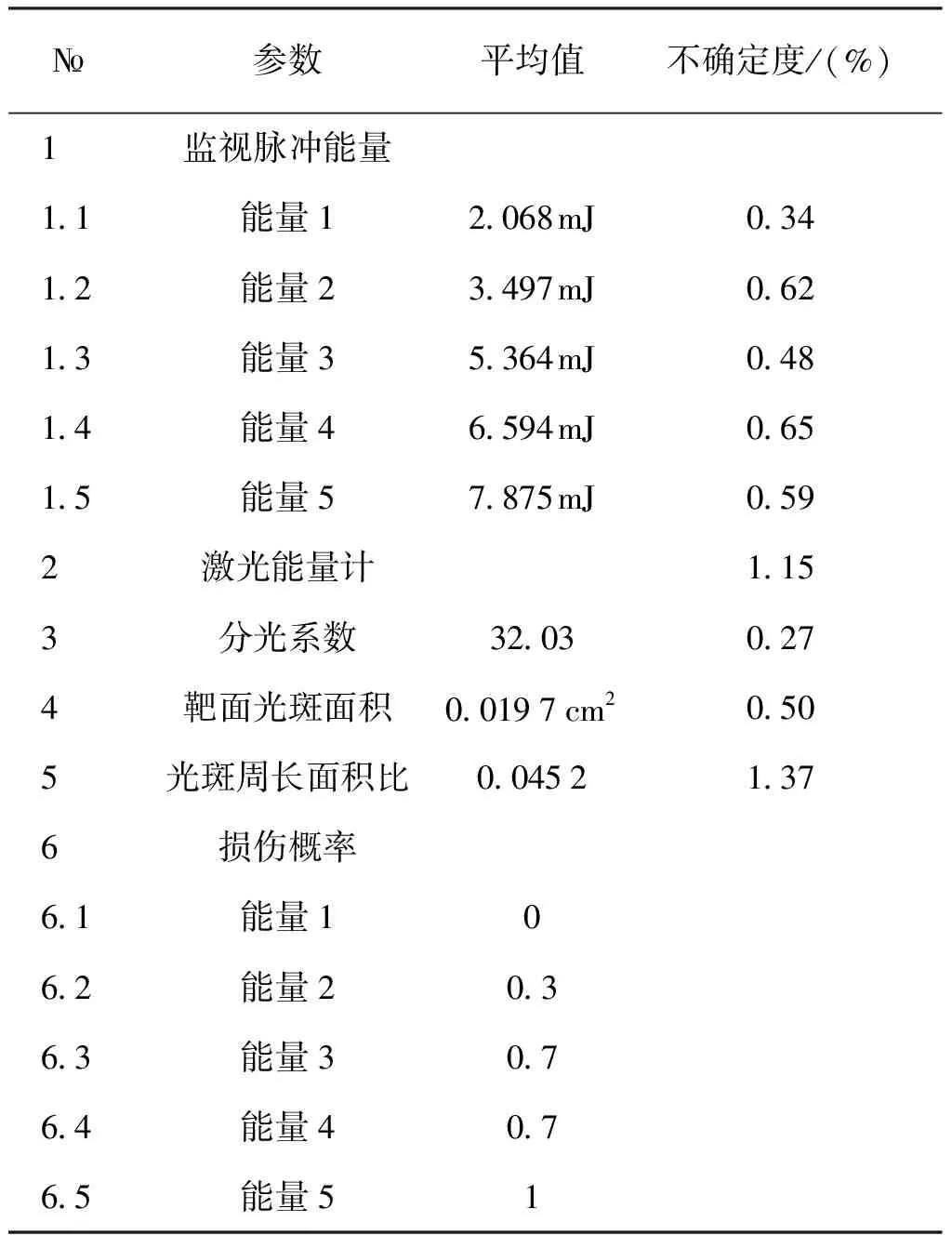
表2 损伤阈值参数测量结果

按照表1所列残差模型，不同残差模型阈值拟合结果如图3所示。

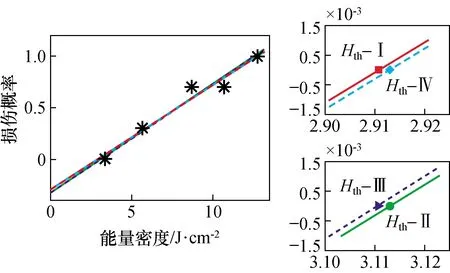
图3 损伤阈值拟合结果

图3中，Ⅰ型阈值拟合结果最小(约2.91 J/cm2)、Ⅱ型阈值拟合结果最大(约3.11 J/cm2)，其原因是表2数据中能量密度误差较大。Ⅳ型与Ⅲ型阈值拟合结果介于二者之间。

不同能量下能量测量结果A类不确定度最大值为0.65%，根据式(25)计算能量密度测量结果相对不确定度uH为2.57%(k=1)。

四种残差模型下损伤概率测量不确定度uP分别为0.088 0、0.089 7、0.089 7、0.088 0，模拟计算uP取最大损伤概率测量不确定度为0.089 7(k=1)。

随机生成一组数目为n、标准差为1、平均值为0的标准正态分布随机数randn(n)，按式(27)、式(28)随机生成一组能量密度和损伤概率数据。

(27)

(28)

损伤概率与能量密度典型模拟结果如图4所示。图4中，模拟数据点围绕实测数据点(Hi，Pi)成二维高斯分布，中心附近数据点较为密集。由于图4中未限制损伤概率的取值范围，因此出现损伤概率大于1和小于0的情况。图4表明，在表2数据测试精度以及均值正态分布假设下，单次测量得到图4中损伤概率大于等于“0”、小于等于“1”的任意数据点都是可能的。

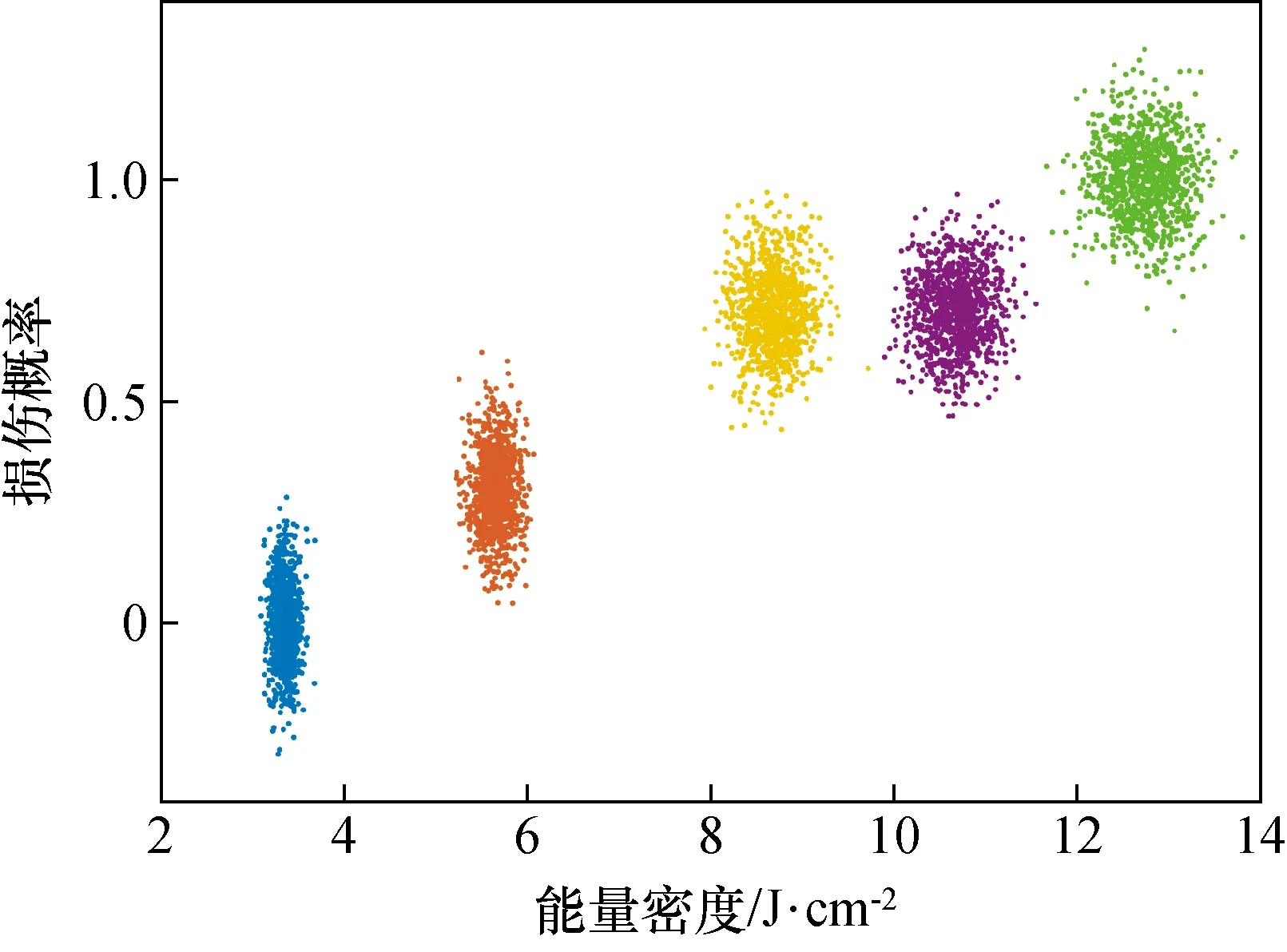
图4 能量密度与损伤概率模拟结果

对应图4按Ⅰ型～Ⅳ型残差模型数值模拟所获结果如表3所示。

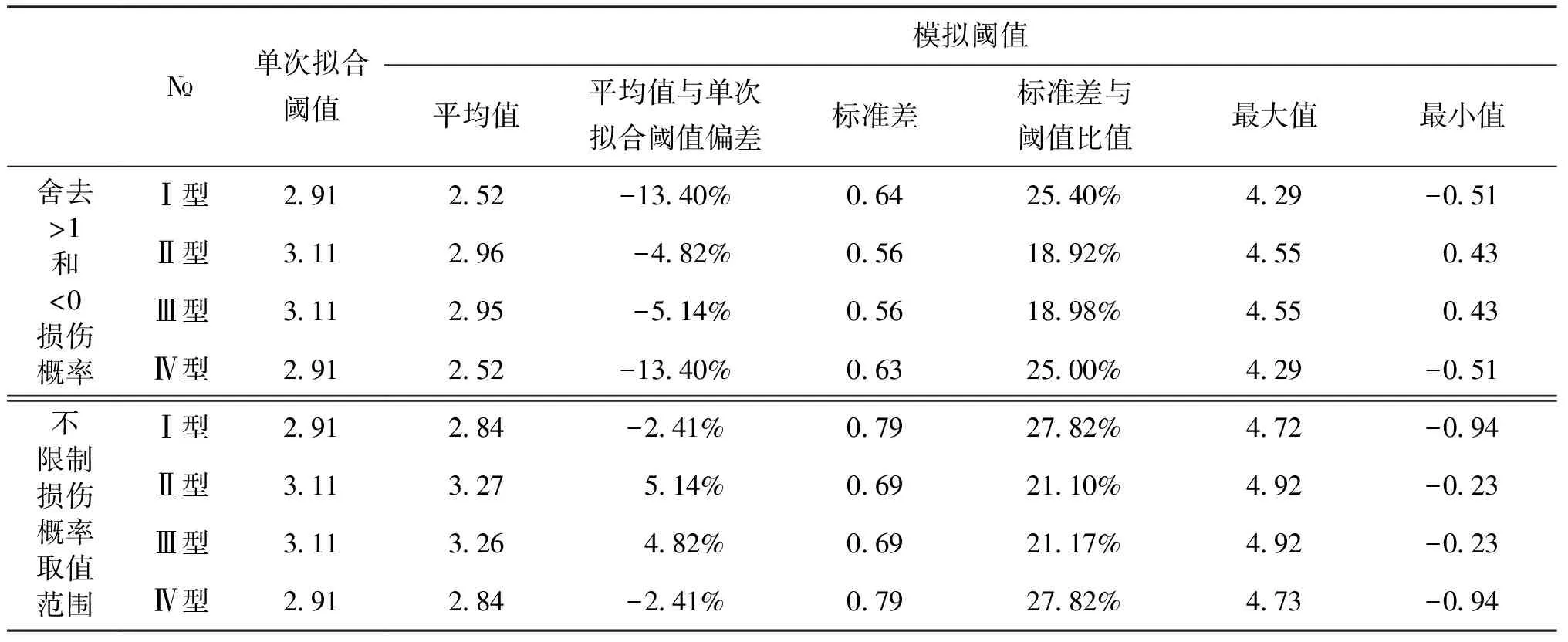
表3 损伤阈值模拟结果

表3中，对比限制损伤概率取值范围与不限制取值范围两种情况可以发现：限制损伤概率取值范围情况下，Ⅰ型、Ⅳ型残差模型获得的模拟阈值平均值与单次拟合获得的阈值之间的偏差约为-13.40%，Ⅱ型、Ⅲ型残差模型约-4.82%、-5.14%。不限制损伤概率取值范围情况下，Ⅰ型、Ⅳ型对应的偏差为-2.41%，Ⅱ型、Ⅲ型对应偏差分别为5.14%、4.82%、。另一方面，从模拟阈值标准差与模拟阈值平均值的比值上看，当限制损伤概率取值范围时，该比值约为25%，当不限制取值范围时，该比值约为19%。从模拟结果上看，不限制损伤概率取值范围的结果偏差较小，因此，后续分析采用不限制损伤概率取值范围的模拟结果。

4种残差模型及表2条件下，损伤阈值概率分布模拟结果如图5所示。

图5中，Ⅰ型损伤阈值概率分布与Ⅳ型结果相似，Ⅱ型与Ⅲ型结果相似，与图3内涵一致。

图5 损伤阈值分布

不限制损伤概率取值范围情况下，Ⅱ型、Ⅲ型残差模型模拟阈值标准差与模拟阈值平均值比值小于Ⅰ型、Ⅳ型所获比值，这意味着Ⅱ型、Ⅲ型残差模型受输入参数误差影响较小，结果较为稳定。

在表2输入条件下，能量密度测量误差对于损伤阈值拟合影响较大，因此Ⅱ型、Ⅲ型结果较为接近。但从表(1)所列残差模型上可以看出，当损伤概率误差较大时，由于Ⅱ型残差模型未考虑损伤概率误差，其模拟结果标准偏差必将增大。综合评价，残差模型Ⅲ更适合作为阈值拟合残差模型，因此，本文后续结果采用Ⅲ型残差模型结果。

连续进行6轮模拟(单轮1 000次)，结果如表4所示。多轮模拟结果表明单轮1 000次的模拟结果较为稳定，可以有效表征测试过程。

表4 损伤阈值多轮模拟结果

拟合直线斜率M与截距b相关系数计算结果如表5所示(6轮)，拟合直线斜率与截距存在相关性，二者不是独立的，在使用公式法进行不确定度评定过程中不能忽略二者的相关性。

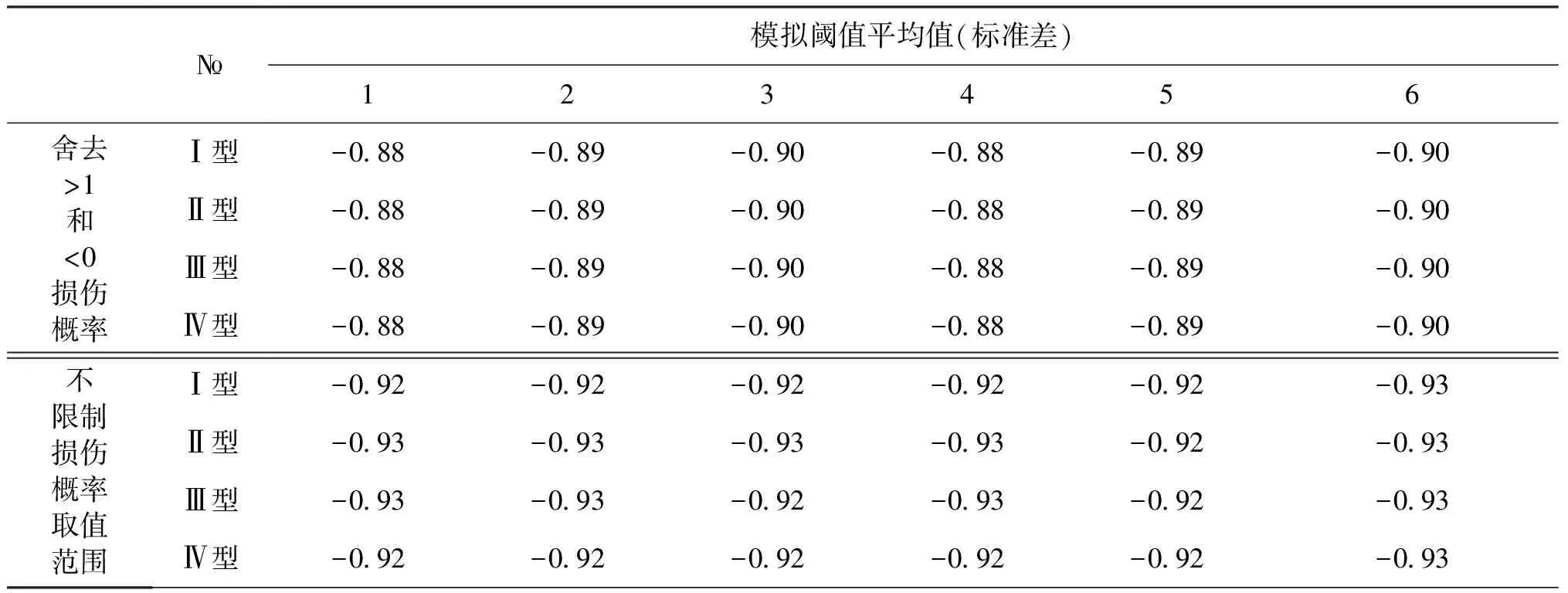
表5 斜率与截距相关系数

取Ⅲ型第一轮损伤阈值模拟标准差作为损伤阈值不确定度(k=1)，损伤阈值测量结果的表示如式(29)所示，取k=2。

Hth=H±kσH=(3.11±1.38)J/cm2

(29)

按Ⅲ型第一轮阈值模拟结果，能量密度区间[1.73 4.49]约占总区间95.7%，与理想正态分布2σ区间所占比例95.45%相差不大，证明蒙特卡洛模拟方法可以较为有效地计算该测量不确定度。

此外，若以[0 3.11]区间概率和作为单点阈值测量值的置信度，在Ⅲ型第一轮模拟结果下损伤阈值3.11 J/cm2置信度约为39.1%。

从损伤阈值测量结果表示上看，本文模拟的损伤阈值测量结果不确定度较大。究其原因是实测损伤概率精度较差、实测损伤概率密度分布与均匀分布偏离较大引起的。

若表2数据中，能量3对应的损伤概率为0.6、能量4对应的损伤概率为0.8时，按照上述计算方法，阈值结果如式(30)所示。可以看出，当损伤概率测试结果基本为均匀分布时，其测量不确定度将大大降低。

Hth=H±kσH=(3.09±0.45)J/cm2

(30)

本文也按照ISO 21254提供的损伤阈值测量不确定度评定方法进行了测量不确定度评定，评定结果如下。

损伤概率不确定度σi/(%):

σ1—2.57；σ2—48.37；σ3—20.86；σ4—20.86；σ5—2.57

不确定度分步计算结果:

M—0.106 1 cm2·J-1；σM—0.003 8 cm2·J-1；b—-0.354 7；σb—0.035 9；H—3.34 J·cm-2；σth—0.36 J·cm-2

结果如式(31)所示,k=2。

Hth=H±kσH=(3.34±0.72)J/cm2

(31)

从计算结果上看，ISO 21254方法所获得的阈值拟合结果偏大，测量不确定度偏小，这将带来测试样品损伤阈值的过高估计。

4 结 论

虽然“零”概率损伤阈值不代表在该能量密度下光学表面一定不发生损伤，但1 on 1激光诱导损伤阈值测试方法作为快速有效的器件抗激光损伤性能评价方法，其适用范围较广，测试成本较低，是一种值得保留的光学表面损伤特性测试评价方法。完整精确地获得零概率损伤阈值的测量不确定度，对正确使用光学表面,合理评价光学表面加工工艺有着积极的意义。

本文在公式法评定激光脉冲能量密度的基础上，基于蒙特卡洛方法对1 on 1损伤阈值测量结果不确定度进行了评定，获得如下初步结论：

(1)当测试光斑尺寸较小时，能量密度测量结果的不确定度主要受能量测量不确定度及光斑周长面积比影响，提高激光脉冲能量稳定性、增大测试光斑面积有助于减小能量密度测量不确定度。

(2)在线性拟合过程中，合理地选择残差模型对于减小拟合方法引入的测量不确定度较为重要。同时考虑损伤概率、能量密度误差的最小二乘法残差模型(Ⅲ型)，抗误差性能最好，可以有效抵消损伤概率、能量密度误差引起的损伤阈值测量值波动。

(3)ISO 21254提供的损伤阈值计算方法及不确定度评定方法，阈值计算结果偏大，测量不确定度偏小，容易发生损伤阈值的过高估计。