一种黏温修正方法的研究与建立

金 愿， 朱绚华， 乔家广

(上海市计量测试技术研究院，上海 201203)

1 引 言

黏度表征流体黏性程度的大小，表示流体抵抗形变的程度，使用过程中分为动力黏度和运动黏度。动力黏度是流体内部抵抗流动性的一种量度，是流动阻力的度量，运动黏度表示重力作用下的流动。流体黏度的大小取决于流体本身，与很多外部因素有关，如温度、压力等。在黏度计量的量传体系中，是以黏度计和标准黏度液交替传递直至样品的黏度值测量。

国内牛顿流体计量已得到较好解决，并开展了一些非牛顿流体计量的相关研究[1,2]。我国牛顿流体计量标准黏度液为精制石油产品、精制甲基硅油[3,4]，具备牛顿流体特性。其中，低黏度标准黏度液为精制石油产品，由精制基础油按一定比例配制；较高黏度标准黏度液为精制甲基硅油，甲基硅油的黏度随聚合度的增大而增大。该类物质黏度特性值均受温度影响很大，在标准黏度液定值及使用过程中需配套精密恒温设备以满足温控的需要。

然而，使用工作黏度计的诸多非标准环境实验室，因其样品黏度特性值受温度影响相对较低，配套恒温设备往往难以保证标准黏度液的使用。在日常校准检测中，常常遇到现场环境无法达到要求，且仪器用户无法将设备送至校准实验室进行校准，需在非标准环境实验室内进行黏温修正。目前，黏度计校准过程中尚未建立精确的黏温修正关系[5,6]。本文在标准毛细管黏度计适用的10～40 ℃最大温区范围内，采用精密恒温水浴槽按照标准黏度液定值方法对选取的精制石油产品、精制甲基硅油标准黏度液做了详细定值，在此实验基础上，采用经典的液体黏温方程系统地分析其黏温特性关系，探讨黏温修正方法。

2 实验部分

2.1 实验材料

实验所用主要材料为GBW(E)130205、GBW(E)130206、GBW(E)130235、GBW(E)130236，即标称值对应为100#、200#、500#、1000#的标准黏度液，前两者为精制石油产品，后两者为精制甲基硅油。

2.2 实验仪器

采用毛细管黏度计标准器组装置，主要包括标准毛细管黏度计组、恒温浴槽及测温设备、电子秒表等。密度测量采用振动式密度计。其中，恒温浴槽温度波动度±0.01 ℃/10 min，均匀性0.02 ℃/10 min；标准毛细管黏度计、振动式密度计、数字温度计、电子秒表均经检定合格或校准后使用。

2.3 黏度定值

对于牛顿流体而言，能够使用密度对运动黏度和动力黏度进行换算。在牛顿流体计量标准黏度液定值过程中，采用国家基准或标准毛细管黏度计定值其运动黏度，通过密度测量，换算出动力黏度，即关系式(1)，进而应用于各类工作黏度计量器具。低黏度标准黏度液为精制石油产品，校准使用时以其运动黏度值为主；较高黏度标准黏度液为精制甲基硅油，校准使用时以其动力黏度为主。

η=ρ·ν

(1)

式中：η为动力黏度，mPa·s；ν为运动黏度，mm2/s；ρ为密度，g/cm3。

按照JJG 154-2012《标准毛细管黏度计检定规程》和JJG 155-2016《工作毛细管黏度计检定规程》中的运动黏度定值方法和要求，选择合适内径的标准毛细管黏度计，在10～40 ℃范围内进行。100#、200#、500#、1000#运动黏度定值结果如图1所示。

图1 运动黏度定值结果

测量500#、1000#的密度值，结果如图2所示。

图2 密度测量结果

由动力黏度与运动黏度关系式(1)，换算500#、1000#的动力黏度，结果如图3所示。

图3 动力黏度结果

2.4 不确定度评定

诸多计量工作者做过关于标准黏度液定值结果的不确定度评定[7～9]。数学模型为：

ν=C·t

(2)

η=ρ·C·t

(3)

式中:ν为运动黏度，mm2/s；η为动力黏度，mPa·s；ρ为密度，g/cm3；C为黏度计常数，mm2/s2；t为流出时间，s。

该定值过程中，标准黏度液运动黏度定值结果不确定度来源包括：黏度计常数引入，时间测量过程中计时器引入、温度影响、重复测量引入。标准黏度液动力黏度定值结果不确定度来源还包括密度引入。标准不确定度分量如表1所示。

表1 标准不确定度分量

取包含因子k=2，求得运动黏度ν和动力黏度η的相对扩展不确定度分别为：

Uν,rel=0.49%

Uη,rel=0.53%

3 黏温特性

3.1 黏温关系方程

黏度来源于分子的热运动和分子间力的相互作用，和温度有着极其密切的关系，不同著者在理论分析与科学实验的基础上给出了一系列黏度-温度关系模型[10～22]。选取典型液体黏温关系方程:

(1)Arrhenius方程[10]：y=A·exp(ΔE/R·x),两边取指数得lny=A+B/x

(2)Walther方程[11]：lglg(y+0.7)=A+B·lg(x)

(3)Namburu方程[12]：lgy=A·exp(B/x)

(4)Andrade方程[13,14]：y=A·exp(B/x+C·x)

两边取指数得lny=A+B/x+C·x

(5)Jane方程[15]：y=A+exp(B/x+C/x2)

两边取指数得lny=A+B/x+C/x2

式中：y为运动黏度，mm2/s，或动力黏度，mPa·s；x为温度，K；ΔE为黏流活化能；R为摩尔气体常数；A、B、C是与流体有关的常数。

其中，Arrhenius方程具有理论意义，可以通过黏流活化能ΔE大致判断流体黏度的大小，在动力黏度-温度拟合中应用广泛。Andrade方程、Jane方程是基于Arrhenius方程的多项式，具有更好实用性。Walther方程常用于绘制石油产品运动黏度-温度关系图，被美国材料与试验协会的ASTM标准采用。Namburu方程遵循Arrhenius方程指数形式，由Namburu等人基于统计分析给出，对牛顿性质纳米流体有很好的拟合效果。

由实验测得的黏温关系只是一些离散点，采用上述多项式分别拟合黏温方程，并分析其拟合精度。为考察拟合参数对分析结果的影响，计算其拟合后的平均偏差β、最大偏差γ。

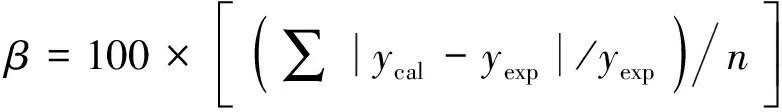
γ=100×Max[|ycal-yexp|/yexp]

式中：ycal为由黏温方程计算得到的黏度值；yexp为由实验测得的黏度值；n为拟合时使用的数据点数目；100×|ycal-yexp|/yexp为黏度拟合相对偏差。

用典者为了表达 “将出来做官或比喻相友善者援引出仕”与“将做官而互相庆贺”的典义，便决定运用《汉书》七二《王吉传》：“吉与贡禹为友，世称‘王阳在位，贡公弹冠’，言其取舍同也。”这一语典，为了适合不同的诗文创作语境，用典者创造了“弹冠”与“弹冠相庆”这两个典面。

3.2 结果与分析

实验在10～40 ℃最大温区范围内定值了所选100#、200#精制石油产品标准黏度液和500#、1000#精制甲基硅油标准黏度液，温度间隔约为2.5 ℃。采用选取的液体黏温关系方程对100#、200#进行运动黏度-温度回归拟合，对500#、1000#进行动力黏度-温度回归拟合。拟合参数及其统计分析结果如表2至表5所示。

表2 100#标准黏度液拟合参数及其统计分析结果

表3 200#标准黏度液拟合参数及其统计分析结果

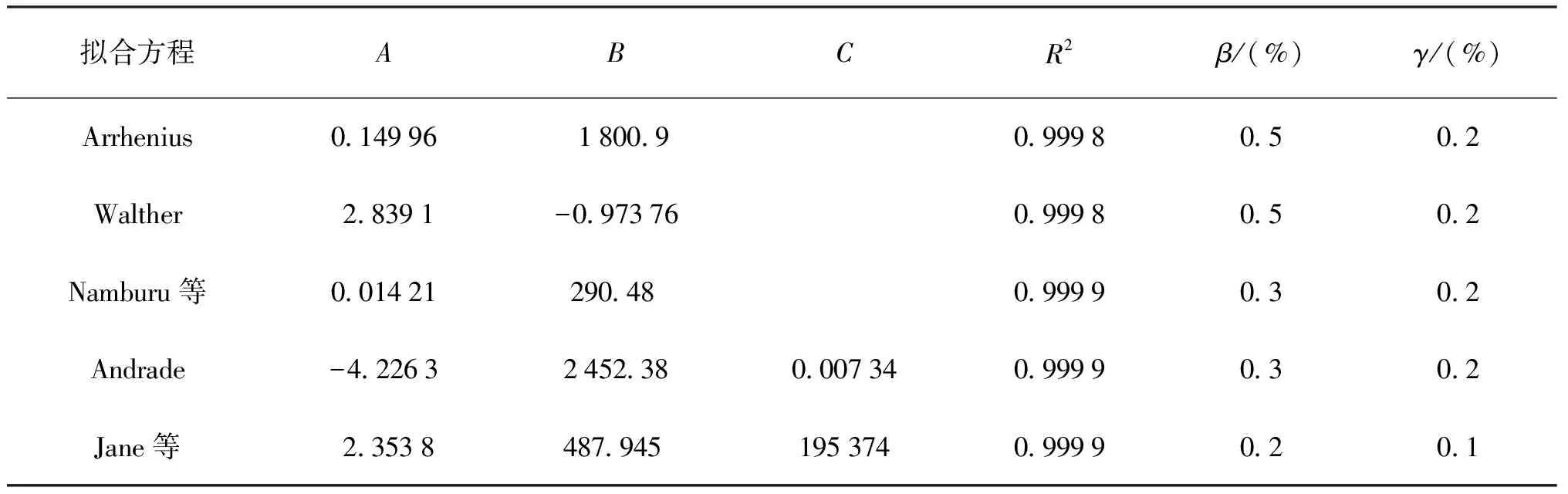
表4 500#标准黏度液拟合参数及其统计分析结果

表5 1000#标准黏度液拟合参数及其统计分析结果

可以看出，采用5个黏温关系方程拟合均具有较为不错的效果，所选精制石油产品和精制甲基硅油标准黏度液具有很好的黏温曲线拟合特性。其中，三项式Andrade方程和Jane方程拟合结果的相关系数均为0.999 9，说明对所选精制石油产品和精制甲基硅油标准黏度液在该温区具有很好的适用性。其中，对于精制石油产品标准黏度液，拟合结果最大偏差为0.9%，对于精制甲基硅油标准黏度液，拟合结果最大偏差为0.3%。

就二项式Arrhenius方程、Walther方程、Namburu方程拟合结果而言，Walther方程对于精制石油产品标准黏度液运动黏度-温度具有很好的拟合效果，Arrhenius方程对于精制甲基硅油标准黏度液动力黏度-温度具有很好的拟合效果。前者拟合结果的相关系数均为0.999 9，拟合100#标准黏度液平均偏差为0.3%，最大偏差为0.8%，拟合200#标准黏度液的平均偏差为0.3%，最大偏差为0.6%。后者拟合结果的相关系数分别为0.999 8、0.999 9，拟合500#标准黏度液平均偏差为0.2%，最大偏差为0.5%，拟合1000#标准黏度液平均偏差为0.1%，最大偏差为0.2%。

图4 黏温关系拟合

4 黏温修正

4.1 黏温修正方法

把Walther方程看成lg(T)的线性函数，Arrhenius方程看成是1/T的线性函数。线性函数具有2点式的函数特征，已知任意两点可以计算直线方程，即能求出其它温度所对应的黏度值。目前国家标准黏度液的标准值是在20 ℃下定值的，日常工作中往往另作25 ℃定值使用。鉴于Walther方程对于精制石油产品标准黏度液运动黏度-温度具有很好的拟合效果，Arrhenius方程对于精制甲基硅油标准黏度液动力黏度-温度具有很好的拟合效果，在此基础上建立黏温修正。

将20、25 ℃作为参考温度点，用100#、200#在20、25 ℃定值的结果计算出log(T)、lglg(ν+0.7)，500#、1 000#在20 ℃、25 ℃定值的结果计算出1/T、lnη，代入线性方程y=A+B·x。计算出相关常数A、B，即得黏温修正关系式，如表6和表7所示。

表6 精制石油产品标准黏度液黏温修正式

表7 精制甲基硅油标准黏度液黏温修正式

大量使用的常规工作黏度计，诸如旋转法黏度计及各类涂料杯等的精度在2%及以上，使用工作黏度计的诸多非标准环境实验室日常工作环境在15～30 ℃温区。

鉴于此，在该温度区间考察黏温修正关系式计算精确度，将黏温修正关系式计算结果与定值结果进行比较，相对误差与温度之间关系如图5所示，其中，横坐标表示温度，纵坐标表示相对误差。在15～30 ℃温区内计算结果较定值结果的最大偏差为0.65%。其中，对于低黏度标准黏度液的运动黏度值，100#的最大偏差为0.60%，200#的最大偏差为0.62%；对于较高黏度标准黏度液的动力黏度值，500#的最大偏差为0.65%，1 000#的最大偏差为0.35%。该修正方法的计算精确度能满足需要。

图5 计算结果与实验结果的比较

4.2 准确性验证

校准结果示值误差以系数K表示，实验值计算的系数记为参考值Kref，计算值计算的系数记为检验值Klab，校准结果如表8和表9所示。

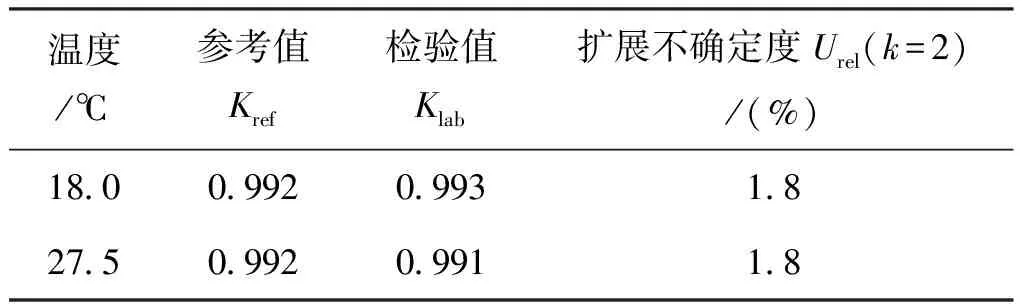
表8 黏度杯校准结果

表9 旋转黏度计校准结果

校准结果满足检定或校准结果的验证公式[25]，结果可信。

5 结 论

本文依据实验定值的黏温数据，系统地分析了所选精制石油产品和精制甲基硅油标准黏度液的黏温特性；选择优化了Walther方程、Arrhenius方程，对精制石油产品标准黏度液的运动黏度-温度、精制甲基硅油标准黏度液的动力黏度-温度建立了黏温修正关系式。将黏度校准工作温度范围拓展到15～30 ℃温区，采用黏度杯和旋转黏度计进行应用尝试，结果表明本修正方法能满足该类工作计量器具校准的需要，实现了在非标准环境实验室内较为准确的黏温修正。