基于天线方向图与近场SBR的海面舰船复合散射研究

张颖 刘伟 时卫莉 郭立新

（西安电子科技大学物理与光电工程学院，西安 717071）

引 言

目标特性是雷达回波中携带的目标特征信息，而近场目标特性往往包含有更多的目标特征信息，其研究具有广泛的应用前景[1]. 在近场条件下舰船目标不能被看成点目标，而是由多个散射中心组成的分布式目标，且各散射中心到天线之间的距离不同，因此各散射中心接收到的入射波有较大的相位差，而不再是平面波. 此外，由于受到天线方向图的影响，目标上各面元接收到的能量有较大差异，当天线和目标之间的距离足够小使得天线的主瓣不能完全照射目标时，会出现局部照射现象.

Gendelman等[2]为了加快物理光学(physical optics,PO)算法计算近场电磁散射的速度提出多级曲面网格法，这种方法将目标平面部分采用大网格，曲面部分采用曲率半径调制网格剖分尺寸，从而减少目标的总体剖分面元数目以此来减少计算量. Gordon[3]为了得到目标近区散射场，将目标剖分成小面元，使用PO获得每个小面元的复散射幅值，再叠加独立的近场相位信息. 孔蓓蓓等[4]提出了新的矩量法-物理光学法(method of moment-physical optics, MoM-PO)混合方法，该方法使用Gordon积分计算目标的PO区域对MoM区域的作用，并加入近场近似处理. 由于PO仅考虑了入射场照明区域的表面积分，忽略了目标表面棱边绕射效应，Ufimtsev[5]提出了物理绕射理论(physical theory of diffraction, PTD)，从经典二维劈边结构的解析解中去掉PO分量得到PTD绕射系数. 梁子长等[6]使用迭代物理光学(iterative PO, IPO)方法计算了角反射器和腔体的近场雷达散射截面积(radar cross section, RCS). 崔铁军等[7]提出了一种时域方法来计算近场时域物理光学(time domainphysical optics, TD-PO)积分，修正Green函数将表面积分简化为一个围线积分，分析脉冲平面波照射下三维导体目标的瞬态电磁散射. Jeng[8]对目标模型采用小面元剖分，修正PTD与弹跳射线(shooting and bouncing ray, SBR)混合方法，计算了球面波入射下目标近场电磁散射. 郭广滨等提出了一种精确有效的物理光学近场积分表示方法，并将其引入到SBR法中计算了偶极子照射下电大尺寸复杂目标的近场散射[9]；又通过引入表面梯度定理和表面散射定理建立了理想导体表面在偶极子照射下近场后向散射的TD-PO轮廓积分表示方法[10]；还对电偶极子照射下目标近场做了分析[11]. 赵华[12]基于高频近似算法探讨了在实际喇叭天线照射下目标的近场散射特性. Wei Yang等[13]基于格林函数的扩展相位近似，提出了一种基于高频方法的近场PO公式，用于模拟电大尺寸目标在近场区域的电磁散射. T. He等[14]提出了一种半解析的方法来计算均匀和各向异性等离子体中极低频电偶极子的近区场. B. Chen等[15]提出了一种改进PO和等效边缘电流积分计算近场散射的算法，其保持了经典算法的简单性和计算效率，可直接应用于近场散射问题.

但鲜有文献报道研究实际天线波束照射下目标和海面的复合近场散射问题. 因此，本文将近场PO方法和SBR法相结合，解决舰船及其与海面多次散射问题. 根据实际天线的方向图建立波束照射目标的散射模型图，研究了天线和目标之间距离以及天线方向图对目标近场散射特性的影响，此外还分析了天线波束照射下目标和海面的近场复合电磁散射问题.

1 仿真模型介绍

1.1 天线方向图与局部照射

瑞利远场准则给出了满足远场条件的最小距离[1]

式中：D表示目标线度；λ表示入射电磁波的波长. 当目标和天线之间的距离大于Rmin时，目标处于远区场，否则目标处于近区.

由于受到天线方向图的影响，目标各个部分在近场条件下接收到的发射天线电磁波的幅值、相位、角度会有较大差别. 如图1所示，D为目标的最大尺寸，Rlocal为发射天线与目标之间的距离， θA为发射天线主瓣宽度， ψ为目标对天线张角. 可知当ψ=2arctan(D/2R)时，将出现局部照射现象[16]，即

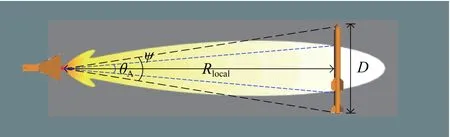
图1 天线波束照射目标示意图Fig. 1 Schematic of target illuminated by antenna beam

由于天线的主瓣宽度一般较小，即当 θA小于0.21时[17]，可给出判定局部照射的最大距离：

当发射天线和目标之间的距离大于Rlocal时，发射天线的主瓣完全覆盖目标. 否则，目标不能被发射天线的主瓣完全覆盖，此时将会出现局部照射现象.

为说明局部照射现象，将图1中的天线放置于目标正上方且垂直指向目标的中心位置，目标为某型号舰船，长约为150 m. 主瓣宽度约为0.24 rad. 由式(3)计算得知当目标距离导弹625 m时，该舰船被天线主瓣完全覆盖. 图2给出了天线位于舰船正上方时舰船的局部照射情况. 可以看出当导弹和目标间的距离为100 m时，舰船只有一小部分被照亮，此时的舰船处于局部照射情况. 当距离增加到400 m时，舰船被天线主瓣照射的部分有所增加，但是船头和船尾仍然没有被主瓣照射. 当距离增加到1 000 m时，虽然都处于被主瓣照射的情况，但舰船各部分的电场强度可以看出并不均匀. 当距离增加到5 000 m时目标相当于一个点目标，目标各部分被天线均匀照射，接收到的电磁波可以被看成是平面波.

图2 导弹位于舰船正上方不同距离时的照亮情况Fig. 2 Illumination of missile over ship with different illumination distances

1.2 近场SBR算法

如图3所示，在近场条件下，目标上各部分接收到的入射场强度、方向和相位是有差异的，此时不宜将基于远场近似的算法应用于目标. 按照入射波长的三分之一或者其他尺度将目标表面剖分成小三角面元网格. 以粗剖(λ /3)面元为例，按照远近场的划分条件即 2D2/λ，可以计算得到小面元的近场距离范围是 2λ/9，显然对于每个面元来说基本上满足远场条件. 因此，即使目标处在近场区域，对单个面元依然可以采用远场近似方法计算其散射场，如图3所示.

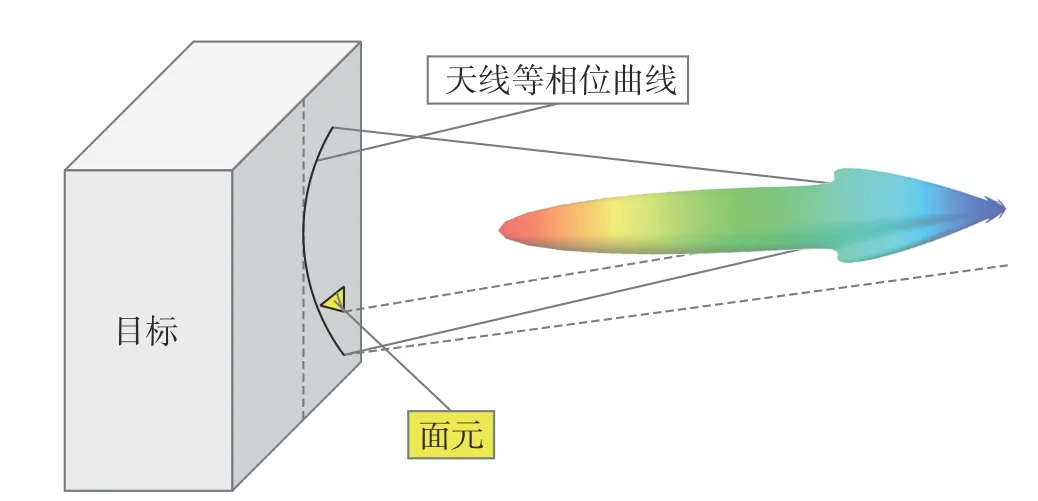
图3 目标近场但面元处于远场的示意图Fig. 3 Sketch of target in near field and facet in far field

如图4所示假设三角面元Sn的最大尺寸为d，S和P分别代表发射天线和接收天线的位置，其位置矢量分别为rS和rP，三角面元上的位置点到场点的距离为R，三角面元中心点O′的 位置为rn.

图4 天线照射三角面元散射示意图Fig. 4 Scattering diagram of triangular panel irradiated by antenna

如果发射天线到目标三角面元Sn上 点的距离 ρ满足|ρ|>2d2/λ， 目标上的面元Sn接收到的电磁波为

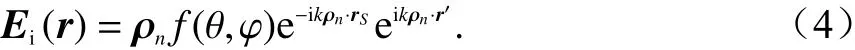
式中，f(θ,φ)是发射天线的方向图函数. 远场条件下的PO公式为

式中，k和η分别表示波数和空间波阻抗. 同样，如果接收天线到目标三角面元Sn上点的距离R满足式(1)远场条件，则R可以近似表示为

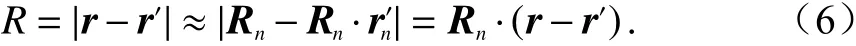
因此，式(5)可以写为

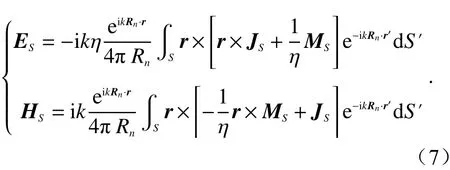
其中面电流JS和 面磁流MS分别表示为：

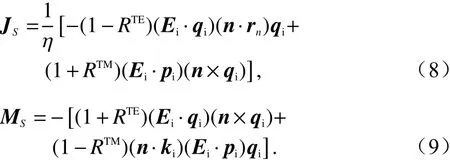
式中：qi表 示入射电场方向；pi表示入射磁场方向；RTE、RTM分别表示TE波和TM波在介质分界面处的反射系数. 将式(8)、(9)代入式(7)，可得

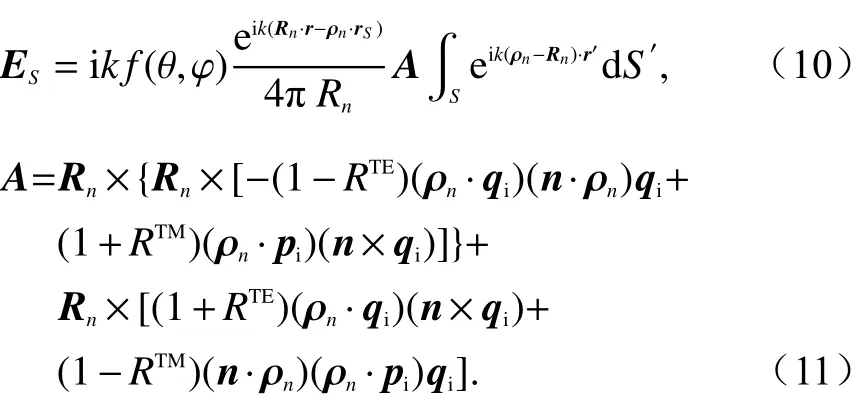
积分可以用Gordon积分计算：

式中：T为w在多边形上的投影长度；M为多边形棱边的数量，在本文中使用的是三角面元所以M=3；am为 多边形第m条棱边的矢量；rm为多边形第m条棱边中点的位置坐标；w=ρn−Rn.

2 算例与分析

2.1 简单目标电磁散射特性

为验证本文波束照射下目标近场散射特性计算方法的正确性，通过使用同一天线源照射平板上立方体目标模型，对比本文方法的计算结果和数值方法的计算结果. 如图5所示，一个边长为2 m的正方形平板正中心放置一个边长为0.4 m的立方体；然后将入射频率为3 GHz的电偶极子在图5的右上角照射目标. 图6所示为电偶极子在距立方体底部中心位置半径1 m处，入射频率为3 GHz，水平极化，分别从入射角为 θi=0°到 θi=85°， 且 φi=0°照射目标时的单站近场RCS. 虚黑线为MoM的计算结果，实红线表示SBR-PO的计算结果. 将MoM与本文方法计算单站近场RCS的结果对比，二者相比的均方根误差为2.77 dB，且在多数角度范围内吻合较好，说明用本文方法计算近场RCS是可行的. MoM运行时间和占用内存分别为32 min和480 MB，SBR-PO运行时间和占用内存分别为3.5 min和62.59 kB，显然运用SBR算法计算近场复合散射时在计算时间和占用内存上都更有优势.

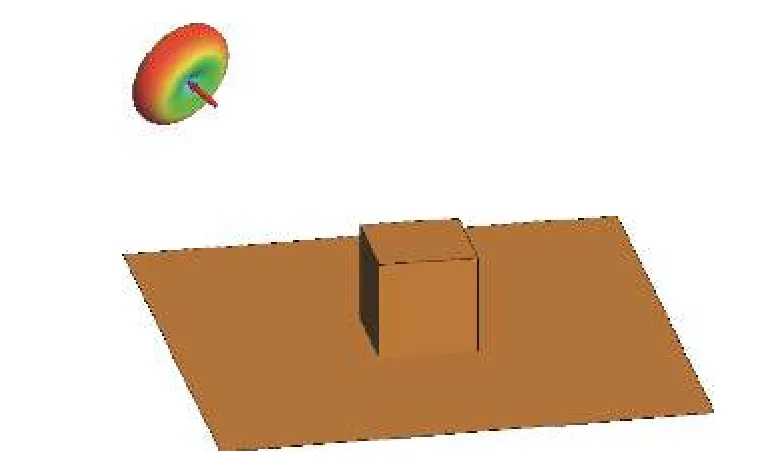
图5 电偶极子照射组合目标示意图Fig. 5 Composite target of electric dipole irradiation

图6 电偶极子照射下组合目标的单站近场RCSFig. 6 Near field monostatic RCS of composite target irradiated by electric dipole

2.2 单纯舰船近场散射特性

如图7(a)所示，矩形孔天线照射一个缩比的舰船模型，长、宽、高分别为4.38 m、0.6 m和0.84 m.发射天线频率为3 GHz，主瓣宽度为0.24 rad. 依据前文推导可得远近场判定距离为383.7 m，局部照射判定距离为18.25 m. 发射天线从舰船的正上方照射，接收天线俯仰角为−90°到90°，图7(b)～(d)分别给出了天线距目标不同距离情况下的双站散射强度，其中实线表示发射天线仅考虑主瓣照射时目标的近场RCS，虚线表示天线有旁瓣时目标的近场RCS.图7(b)显示在距离较近时考虑旁瓣照射的目标RCS比仅考虑主瓣照射时的目标RCS大，造成这种现象的原因是目标上没有被天线主瓣照亮的部分天线的副瓣对其散射特性起到了重要作用. 总体而言两个结果之间的差异随着距离的增加而变小，当距离大于18.25 m，图7 (d)计算结果趋于一致. 此时主瓣可以完全照亮目标，副瓣对目标RCS几乎没有影响.

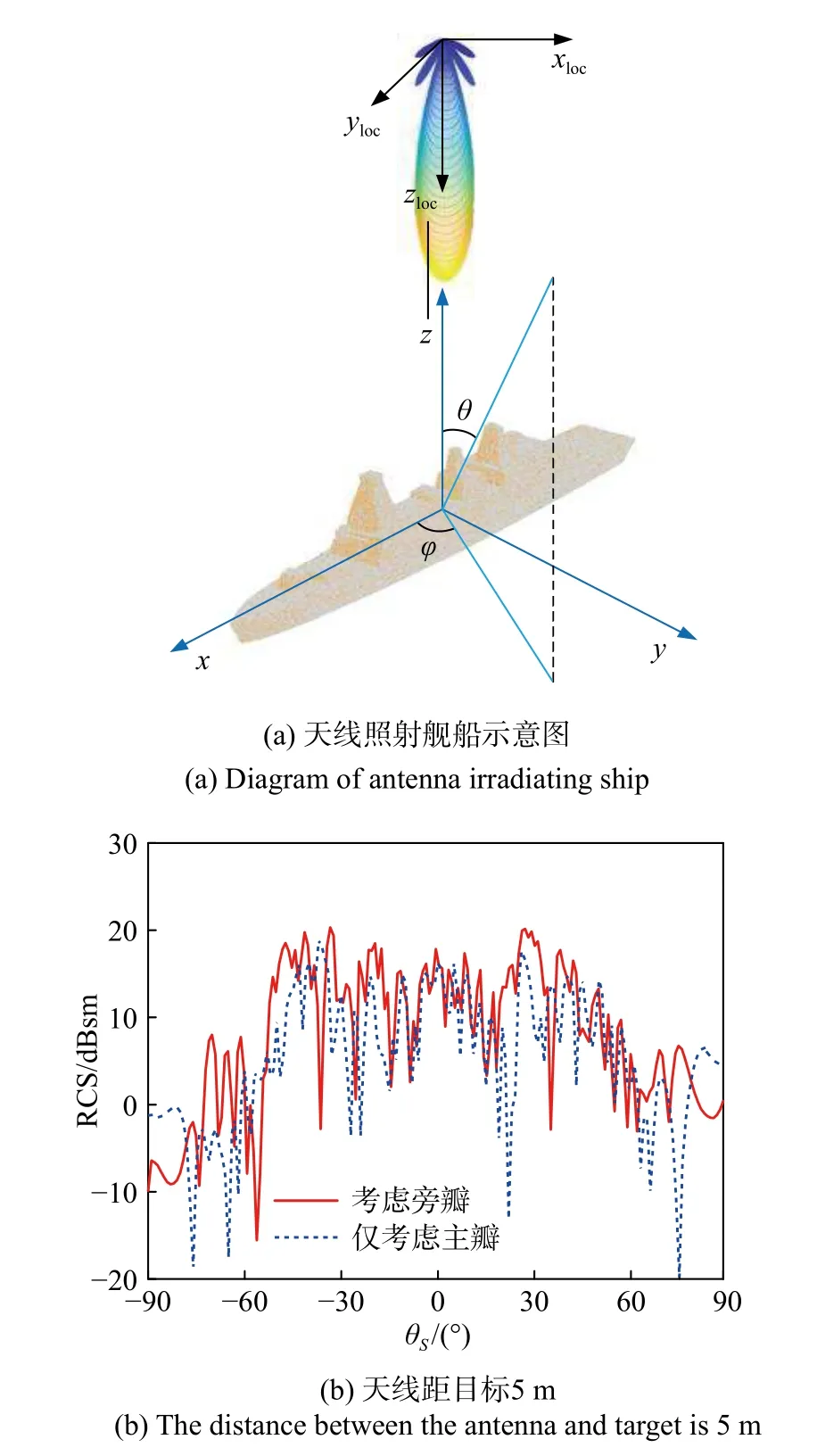
图7 天线与目标在不同距离下天线方向图对舰船RCS的影响Fig. 7 Near field RCS of ship at different distances between antenna and target

图8为矩形孔衍射天线在方位角为 9 0° (拦腰)和0° (迎头)入射时，不同天线和舰船间的距离条件下舰船近场RCS随俯仰角的变化情况. 舰船目标的线度是0.6 m，局部照射判定距离仅为2.5 m. 可以看出：在入射方位角为 90°时，随着天线和目标之间的距离增加，舰船近场RCS也在明显增加；在入射方位角为0°时，散射结果并没有明显的增加，只在俯仰角−15°到 1 5°之间有明显的变化. 这是因为在入射方位角为 90°时，局部照射判定距离为18.25 m，不同照射距离或存在局部照射现象，或存在天线波束对舰船的非均匀照射；而在入射方位角为 0°时，特别是在大角度入射时，天线主瓣可以覆盖整个目标，基本不存在局部照射现象，不同照射距离对舰船RCS的影响较小；在俯仰角 −15°到 1 5°范围内，由于方位角的影响减弱，舰船的长度又成为影响波束照射的主要原因.

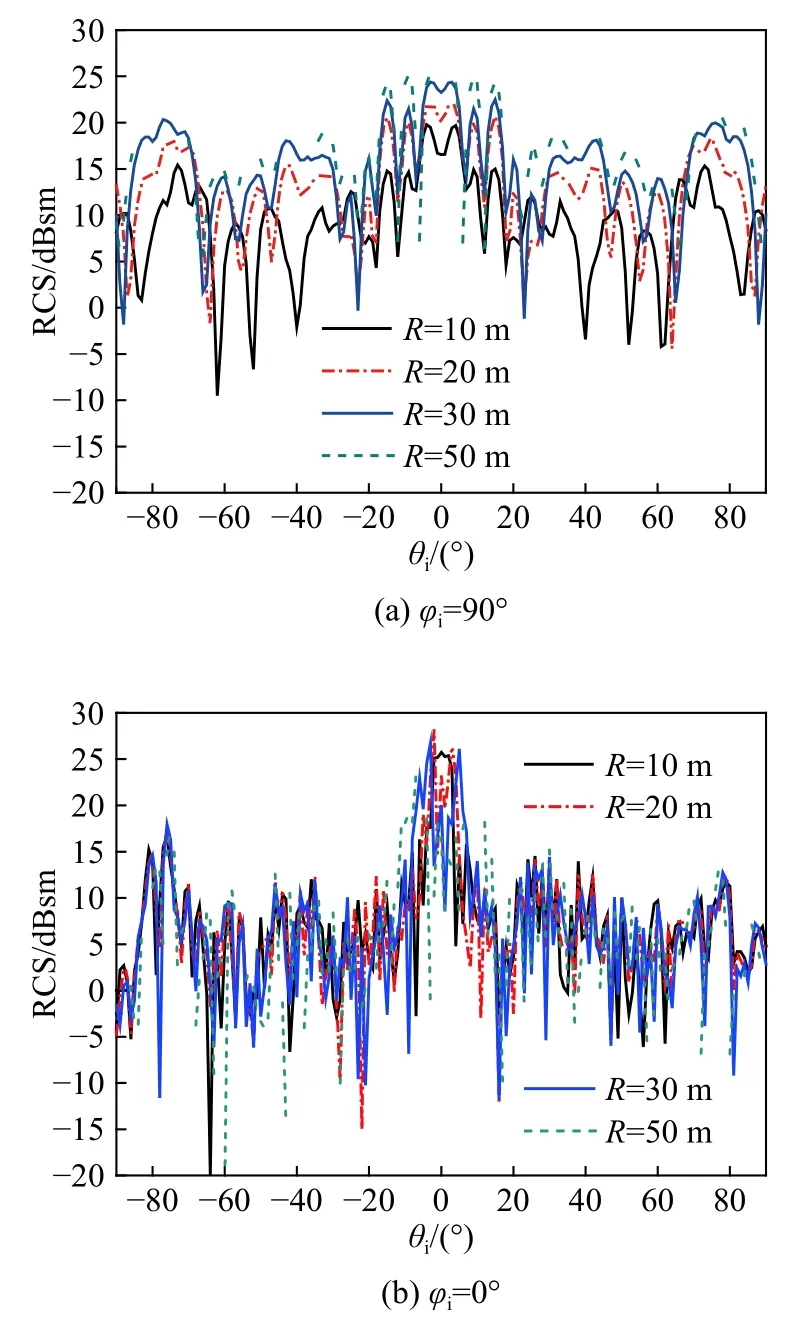
图8 不同方位角下天线距目标不同距离时目标的单站近场RCSFig. 8 Near Field RCS of ship at different distances between antenna and target

2.3 海面舰船近场复合散射特性

取海面大小为100 m×50 m，风速U10为5 m/s，风向角为 0°，舰船目标长、宽、高分别为60 m、10 m和20 m，图9为喇叭天线和复合模型的距离为100 m时，入射方位角为 90°，入射频率均为3 GHz，俯仰角在−90°到90°范围内的单双站近场复合电磁散射，其中图9(b)的入射角为60°. 如图9(a)所示，在小角度时海面对单站复合电磁散射的结果影响较大，而在大角度入射时，海面对复合散射几乎没有影响. 图9(b)所示在后向上目标对复合散射的影响较大，而海面对复合散射影响较小，但在镜向方向上海面对复合散射的结果影响较大；此外双站散射结果中在入射方向的镜向和后向上有峰值，这和远场情况下的散射特性是一致的.

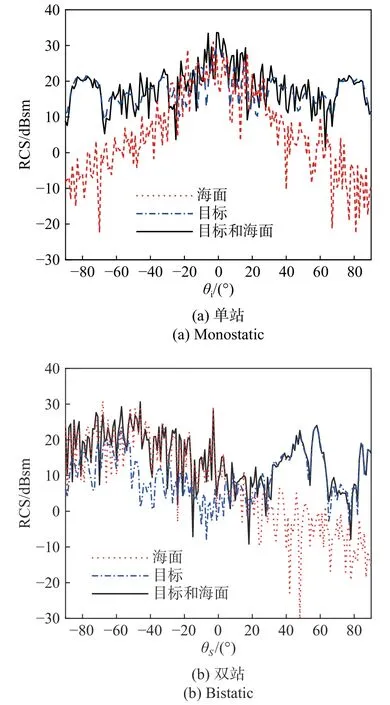
图9 波束照射下船与海面的复合单双站近场RCSFig. 9 Composite monostatic near-field RCS from target above sea surface under beam irradiation

取波束入射方位角为 90°，图10所示为yoz面内天线在俯仰角为 −90°到 9 0°范围内风速对复合模型近场后向散射的影响，这里天线与复合模型中心的距离为1 000 m，即处于近场散射区域. 可以看出：图线的左右两部分具有高度的对称性，这是因为此时天线正对舰船侧面，而舰船的两侧是对称的；舰船目标在单站近场复合电磁散射特性中影响较大，这和远场情况下一致的. 另外风速越大，复合散射镜向散射强度越小，这是因为风速越小，海面的镜向散射强度增大，同时海面镜向散射强度的增大会增强海面与舰船目标的耦合作用.

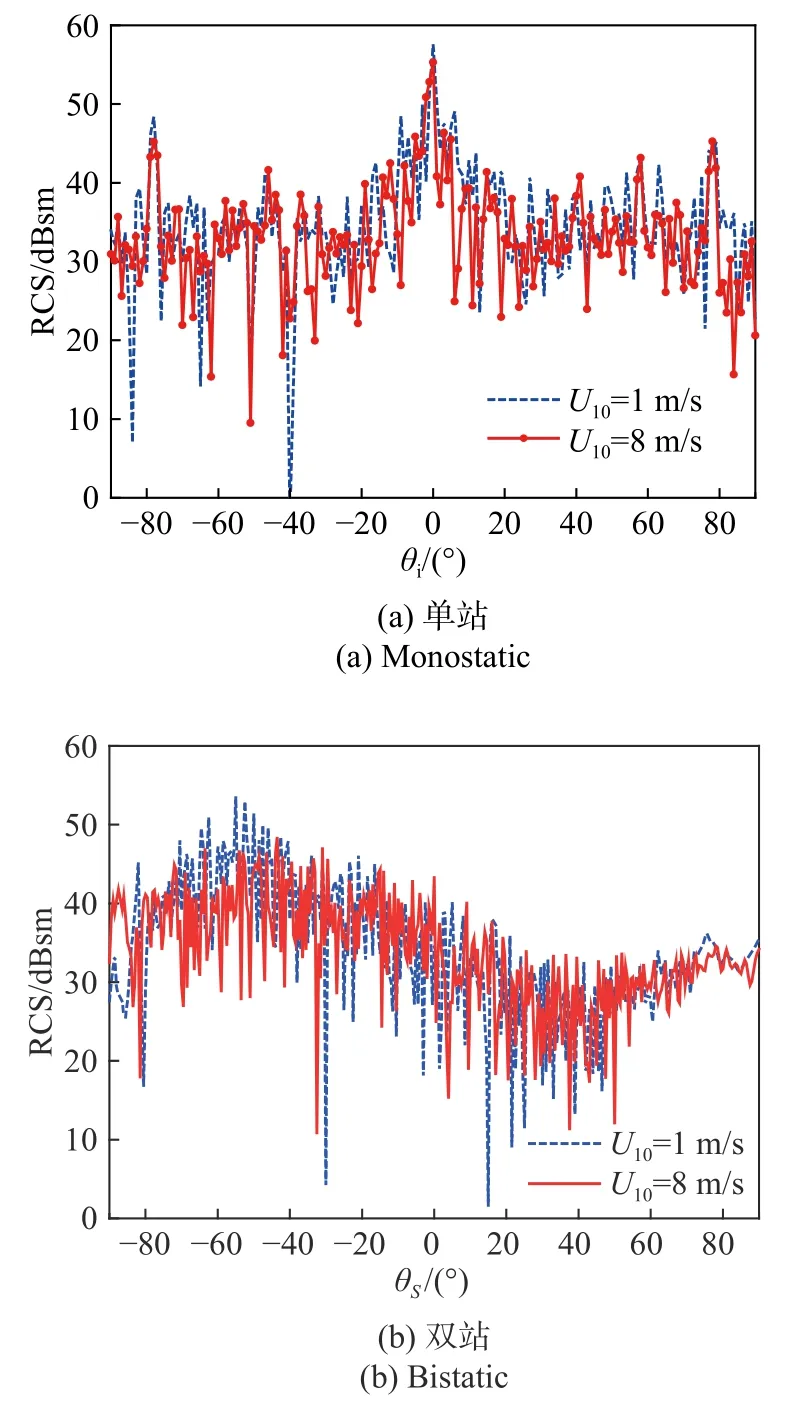
图10 不同风速下目标和海面的复合近场RCSFig. 10 Near field composite electromagnetic scattering of target above sea surface under different wind speeds

3 结 论

针对实际天线照射下复合电磁散射特性研究，本文给出了目标近场面元的远场PO公式，并结合天线方向图应用于SBR法计算目标近场散射特性. 通过相关分析可知：舰船与天线之间的相对方位对单站近场散射特性具有重要的影响；在小角度时海面对目标和海面的单站近场复合电磁散射结果影响较大，而在大角度入射时几乎没有影响；在后向散射区域内目标对近场双站复合散射的影响较大，海面影响较小，而在镜向方向上海面对复合散射的结果影响较大，且风速的影响不能忽视. 本文研究海上目标在天线波束照射下的近场复合散射特性，对引信和导引头的雷达体制设计、地海杂波的抑制具有重要的应用价值，同时天线波束对海上舰船目标的局部照射研究，为提升导弹打击精度与效能提供了理论支撑.

不足之处在于分析波束照射下目标及目标与海面的近场电磁散射特性时，没有考虑距离变化时的电磁散射特性；此外天线始终是正对模型的中心即坐标原点，实际应用中天线不可能一直正对目标中心.