南海海域海表面温度对低空大气波导数值模拟的影响研究

成印河 徐剑辉 张玉生 郭相明 游志伟

（1. 江苏海洋大学海洋技术与测绘学院，连云港 222005；2. 江苏海洋大学海洋遥感大数据应用中心，连云港 222005；3. 中国电波传播研究所 电波环境特性及模化技术重点实验室，青岛 266107）

引 言

大气中异常大气折射率结构会导致电磁波被陷获在一定厚度的大气层内，这种现象被称为大气波导传播[1]. 大气波导环境的存在对无线电通信、雷达探测等系统产生重要影响，导致超视距传播[2]和探测盲区[3]. 大气波导环境参数可以用大气折射率垂直梯度小于零时来描述. 而大气折射率是气温、大气压和水汽压等物理量表示的经验函数[4]，一般采用修正大气折射率M表示，对于微波波段，通常采用以下形式：

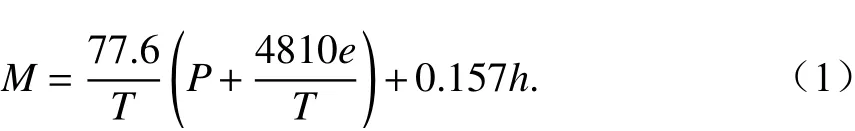
式中：M是无量纲单位，数值上采用M单位；T为气温，K；P为大气压，hPa；e为水汽压，hPa；h为海拔高度，m.

由式(1)可知湿度随高度锐减或者温度随高度递增，或两者同时发生是大气波导形成的必要条件，这种大气结构往往与大气边界层结构密切相关. 已有研究表明，海洋下垫面的海表面温度(sea surface temperature, SST)分布对大气边界层数值模拟具有重要的影响. Doyle等[5]利用中尺度模式MM5(mesoscale model5)分析了不同分辨率的SST对大西洋海域的海洋大气边界层分布的影响；孟宪贵等[6]研究了夏季黄海SST对大气边界层的影响；霍志丽等[7]根据部分海上观测SST分析了东海黑潮海洋锋过程中大气边界层高度的变化. 在海洋大气边界层顶部往往伴随着逆温及湿度锐减的大气结构，容易发生大气波导事件. 由此可知SST可改变海洋大气边界层高度及结构，进而影响大气波导环境特征.

除了海上大气边界层结构变化会直接影响到海上大气波导环境，实际上还有多种因素的影响如地形、风场、海岸线、SST等. 刘桂艳[8]利用中尺度天气预报模式天气研究与预报(weather research and forecaoting, WRF)分析了海陆风过程中发生的大气波导；丁轩茹等[9]研究表明夏季风爆发对南海蒸发波导产生影响；成印河等[10]分析了夏季风爆发对南海南北部低空大气波导的影响；Burk和Thompson[11]使用NORAPS (Navy Operational Regional Atmospheric Prediction System)模拟研究了加州南部海陆风对海洋大气折射率环境的影响；Brooks等[12]指出波斯湾表面波导厚度是沿着风向变化的，跟离岸距离成正比；Atkinson和Zhu[13-14]使用MM5模式研究了海风、沿岸结构、地形等因素对大气波导的影响；Reddy等[15]研究表明在热带近岸海域大气波导环境同样受海陆风环流的影响. 由此可知海洋大气折射率环境受到多种因素的影响，风场是其中一个重要的因素，然而SST是否是影响大气波导形成的一个重要因素呢? Haack等[16]2010年利用4种中尺度数值模式研究分析了美国东海岸的SST对大气波导数值模拟的影响，但其模拟结果是否适用于南海，有待于进一步研究.

南海是西太平洋最大的边缘海，其大气环境受大陆海岸线、季风及下垫面SST分布等因素影响，已有的研究表明海洋边界层高度存在日变化[17-18]，也是低空大气波导的高发区[19-23]，究竟每种因子对南海大气波导环境影响怎样，需要有针对性的研究. 本文基于中尺度天气数值模式WRF，拟开展不同SST分布对南海低空大气波导数值模拟影响的研究.

1 研究方法

1.1 WRF模式配置

为了开展下垫面不同SST对南海低空大气波导数值模拟的影响，本文利用中尺度天气数值模式ARW(Advanced Research WRF)3.6版本开展数值模拟研究. WRF模式是新一代中尺度天气预报模式，已经被广泛地应用于降水、台风等方面的研究. 在WRF模式中，以美国国家环境预报中心提供的气候预报再分析系统(climate forecast system reanalysis,CFSR)再分析资料作为模式的初始场，积分步长为60 s，以(15°N, 115°E)为中心设置了四重嵌套区域，分为南、北两部分共6个区域，具体见图1. 模式垂向采用不等间距分层，底层加密，共分为42层，模拟时间为1998年5月到6月.

图1 研究海区(表示“科学1号”和“实验3号”观测站)Fig. 1 Map of the study area and the cross-shaped stars show the “Kexue 1”and “Shiyan 3” observation stations

为了区别不同下垫面SST分布对低空大气波导的影响，本文数值模拟过程中采用相同的比较成熟的积云、辐射、微物理等参数化方案，具体见表1.

表1 WRF模式通用的参数化方案Tab. 1 Universal parameterization schemes applied in the WRF model

1.2 试验方案设计

在下垫面SST驱动模式过程中，主要设计了3种数据设计试验方案，分析其对南海低空大气波导的影响. 3种数据分别为国家环境预报中心(National Centers for Environmental Prediction, NCEP)提供的CFSR再分析资料中的SST数据、欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)提供的ERA-I (ERA-Interim)再分析资料中的SST数据和美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)提供的OISST(optimum interpolation sea surface temperature)数据[24]，具体时间、空间分辨率见表2.同时表2给出了4组下垫面SST驱动试验方案，其中：Exp-N方案仅保留通用设置，无下垫面驱动场；Exp-C方案和Exp-E方案每6 h更新一次下垫面驱动场SST；而Exp-O方案每24 h更新一次.

表2 SST数值试验方案设计Tab. 2 SST experiment schemes setting

为了研究不同SST对南海低空大气波导的影响，首先我们分析不同SST的差异. 以1998年5月5日为例，我们给出了0时(UTC，下同)的3种SST数据以及ERA-I和 CFSR提供的SST在6时、12时和18时相比0时刻的变化情况，如图2～4所示，并以此估计SST对低空大气波导的影响.

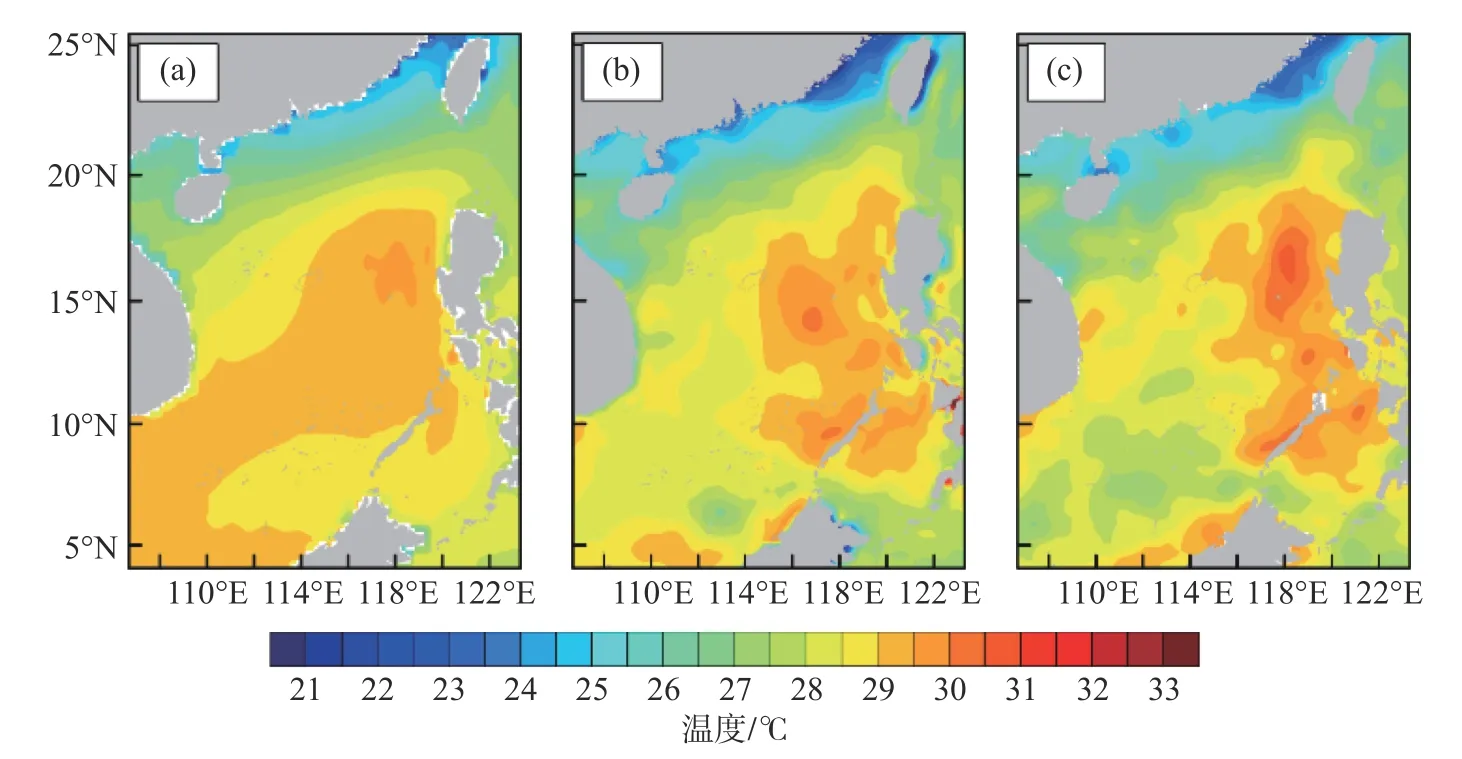
图2 1998年5月5日0时3种SST数据((a)表示ERA-I, (b)表示CFSR, (c)表示OISST)Fig. 2 Distributions of three SST datasets at 0 UTC on May 5, 1998((a) ERA-I SST, (b) CFSR SST, (c) OISST)

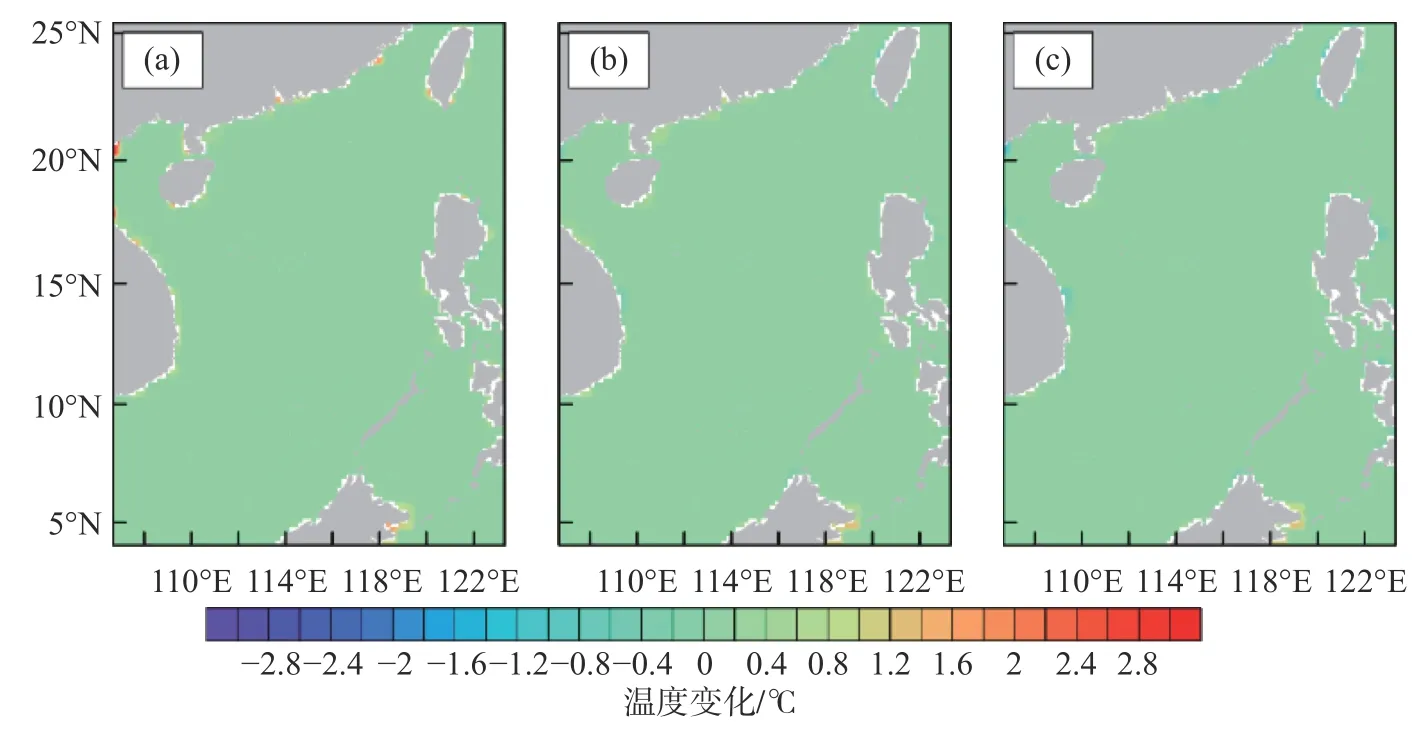
图3 1998年5月5日ERA-I SST数据日变化((a)、(b)和(c)分别表示6时、12时、18时数据减掉0时的差值)Fig. 3 Diurnal variation of the ERA-I SST dataset on May 5, 1998((a)，(b) and (c) show the difference between each time(6，12,18 UTC) and 0 UTC, respectively)

图4 1998年5月5日CFSR SST数据日变化((a)、(b)和(c)分别表示6时、12时、18时数据减掉0时的差值)Fig. 4 Diurnal variation of the CFSR SST dataset on May 5, 1998((a)，(b) and (c) show the difference between each time(6，12,18 UTC) and 0 UTC, respectively)

从图2～4可知，SST区别非常明显. 由于空间分辨率的不同，3种数据都能够表现出SST从南到北的区域空间变化，但ERA-I给出的SST比较平滑，温度跨度比较大，而其他场分辨率较高，能够表征一些海洋现象细节特征. 如以(15°N, 118°E)为中心的区域均有大小不等暖涡，但也有区别，OISST 给出的暖涡范围大，靠近吕宋岛，同时南部有多个的冷涡. 在日变化方面，从低分辨率的ERA-I给出的SST几乎无日变化情况，而CFSR给出的SST存在较为明显的日变化情况，如南海中西部的冷暖涡变化从小变大，然后变小；同时研究区域中陆地西海岸海域存在明显的温差变化，如中南半岛南部海岸附近6时温差由2.8 ℃减弱为凌晨18时的−2.4 ℃以上. 由此推测这种SST分布的不同可能会对南海低空大气波导模拟具有重要的影响.

1.3 探空数据与分析方法

为了对比分析不同试验方案的数值模拟结果，我们与1998年5月5—25日和6月5—25日南海季风试验期间“实验3号”和“科学1号”科考船的GPS探空观测数据作对比. 科考船分别位于南海北部和南部，见图1，北部为“实验3号”科考船位置(20.36°N, 116.84°E)，南部为“科学1号”科考船位置(6.23°N,109.83°E). 在南海季风试验期间分别采集在0、6、12和18时4个时次的气温、相对湿度、露点温度、海拔高度等廓线数据，采样频率为1 s或2 s.该数据经过质量控制[25]后有296个探空廓线用于对比WRF模式的输出结果，该探空站数据几乎平均分布在南海南北两个区域. WRF模式输出的气温、比湿等以两科考船观测时间、空间为中心，时间上相同，空间上采用周围邻近插值方法获得匹配数据，用于开展对比研究.

分析方法主要采用列联表方法用于统计波导发生情况，平均误差和标准差用于波导特征参数定量分析. 列联表是一种矩阵格式的表格，用于多元分类变量的频率分布. Haack等[26]曾利用列联表对美国海军COAMPS(Coupled Ocean-Atmosphere Mesoscale Prediction System)模拟结果与无线电探空仪采集的数据对比分析，研究其预报准确率、虚报率等. 针对低空大气波导特征参数采用平均误差和标准差等公式进行量化，具体见公式(2)和(3).

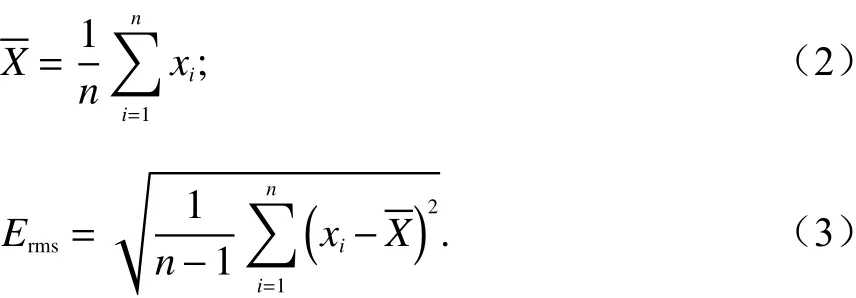
2 结果分析与讨论

2.1 低空大气波导统计分析

为分析不同SST对低空大气波导发生事件的影响，利用各模拟方案的第四重嵌套输出数据分析大气波导发生情况，并与南海两个观测站探空数据进行对比分析，结果见表3.

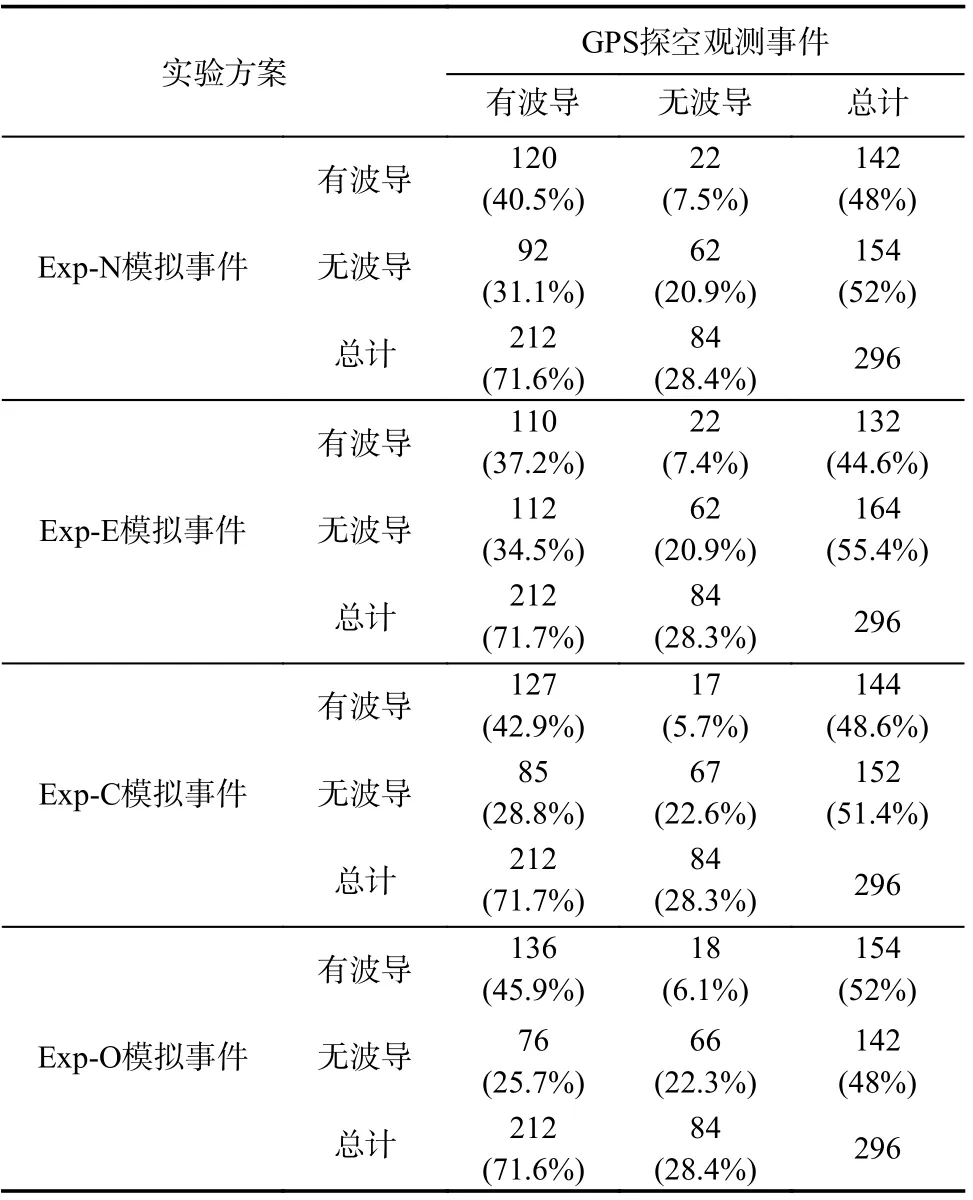
表3 各试验方案中数值模拟与观测的低空波导事件统计Tab. 3 Ducting events statistics for numerical simulation based on each experiment scheme and GPS radiosonde data

由表3可知，各方案的模拟正确率为对角线上两组数据之和(都无波导和都有波导)与观测总数的比值，虚报率为各方案仅数值模拟有波导数与观测中无波导总数的比值，例如Exp-N方案模拟正确率为61.5%，即 (120+62)/296，虚报率为26.2%，即22/84.

从各方案模拟正确率数据可知：Exp-O试验方案最好，正确率最高为68.2%；其次是Exp-C方案(正确率为65.5%)和Exp-N方案(正确率为61.5%)，正确率最低的为Exp-E方案(正确率为58.1%)，即NOAA提供的每24 h更新一次的SST驱动场最好，每6 h更新一次的ERA-I数据中SST的方案模拟最差. 从虚报率数据可知，Exp-O和Exp-C两种试验方案虚报率相当，为21%左右，其他两种方案虚报率都超过26%. 综合正确率和虚报率的结果，在设计的4种试验方案中，Exp-O方案最好，即精细化的SST对数值模拟的低空大气波导事件具有重要的影响，其次是下垫面的更新周期.

为了定量地研究不同SST对低空大气波导模拟参数的影响，基于式(2)和(3)，我们开展模拟的波导参数与探空观测的大气波导参数的对比分析，结果见表4.

标准差用来表征一组数据中离散程度，值越小说明数据越集中；平均误差和其标准差越小，表明该方案越好. 从表4可知，在波导底高中Exp-O方案平均误差与标准差最小，其次为Exp-C方案，Exp-N方案的平均误差最大而Exp-E方案的标准差最大. 在波导强度中Exp-N方案平均误差最大而标准差最小，Exp-E方案平均误差最小而标准差最大，Exp-C与Exp-O方案平均误差与标准差整体较小. 在波导厚度中Exp-N方案平均误差与标准差最小，Exp-C方案平均误差与标准差最大，而Exp-E与Exp-O方案整体较小. 综合波导特征参数平均误差与标准差的模拟结果，在设计的4种试验方案中，Exp-O方案最好，其模拟的波导底高最好，波导强度与波导厚度相对较好，即精细化的SST对数值模拟的低空大气波导事件具有重要的影响，其次是下垫面的更新周期.

表4 数值模拟波导特征参数与探空数据的对比分析Tab. 4 Contrastive analysis of the duct parameter characteristics between simulated results and radiosonde data

为了直观地了解大气波导误差存在位置及原因，以1998年5月13日6时南海南部和1998年6月8日12时南海北部为例，做出了各方案数值模拟和GPS探空观测的修正大气折射率、相对湿度和气温随高度分布，见图5～6.

图5 1998年5月13日6时南海南部模拟和实测参数随高度分布((a)大气折射率, (b)相对湿度, (c)气温)Fig. 5 Profiles of the simulated results and observed parameters in south SCS at 06 UTC, May 13, 1998((a)atmospheric modified refractivity index, (b) relative humidity, (c) air temperature)

从图5(a)与图6(a)不同日期的两种数据的修正大气折射率随高度分布可知，Exp-O方案模拟修正大气折射率随高度分布与GPS探空观测最接近. 由于湿度锐减与逆温是形成大气波导的必要条件，从图5(b)与图6(b)可知，Exp-O方案模拟的相对湿度随高度分布与GPS探空观测整体上最接近，有明显的湿度锐减现象. 从图5(c)与图6(c)可知，各个方案模拟的气温随高度分布相对接近但是在图5(c)中仅Exp-O方案模拟出逆温现象. 综上所述，NOAA提供的每24 h更新一次的SST驱动场最好，其模拟相对湿度与气温的变化更准确，该结果表明精细化的SST对相对湿度和气温数值模拟的重要性，同时也影响了低空大气波导发生概率以及特征参数.

图6 1998年6月8日12时南海北部模拟和实测参数随高度分布((a)大气折射率, (b)相对湿度, (c)气温)Fig. 6 Profiles of the simulated results and observed parameters in the north SCS at 12 UTC, June 8, 1998((a)atmospheric modified refractivity index, (b) relative humidity, (c) air temperature)

2.2 子、母网格模拟结果分析

由于嵌套网格层数的增加，模式的运算时间也随之增加. 在使用WRF模式进行数值模拟研究时，时间成本也是需要考虑的一个重要因素. 以最优的SST数据为驱动场，利用Exp-O方案对比分析了子、母网格数值模拟结果，见表5.

表5 第三、四重嵌套网格模拟结果的低空波导统计Tab. 5 Ducting events statistics for the third and fourth nest grid simulation results.

由表5可知：在都有波导分类中，四重嵌套样本数明显提高，而在都无波导分类中变化不大，这导致四重嵌套网格模拟正确率提高了11.8%；同样地，四重嵌套网格模拟虚报率降低了2.4%. 此外，从三、四重嵌套的有波导总计中可知，模式在四重嵌套网格下模拟发生低空大气的概率为52%，比三重嵌套41.6%提高了10.4%. 表明子网格虽然增加了运算时间但其提高了模拟正确率、降低了模拟虚报率并且提高了模拟发生低空大气波导的概率.

为进一步讨论该方案模拟结果，对比分析三、四重嵌套网格下波导特征参数，见表6.

表6 第三、四重嵌套网格模拟波导特征参数统计Tab. 6 Statistical characteristics of duct parameters for the third and fourth nest grid simulation results

由表6可知，四重嵌套网格模拟的波导底高平均误差与标准差大于三重嵌套而波导厚度平均误差与标准差则小于三重嵌套，四重嵌套网格模拟的波导强度平均误差小于三重嵌套而标准差大于三重嵌套. 表明子网格由于提高了模拟发生低空大气波导的概率，在一定程度上提高了模拟波导底高的误差，但同时也降低了模拟波导厚度的误差.

3 结 论

本文基于先进的中尺度大气模式WRF，利用不同SST开展了南海低空大气波导数值模拟试验，并与GPS探空观测数据进行了对比分析，初步得到了以下结论：

1)在设计的4种方案中，SST精度最高的Exp-O方案模拟结果最好，其正确率为68.2%，虚报率为21.4%，波导底高平均误差以及标准差最小；

2)SST分辨率对南海低空大气波导的模拟影响最大，较高的分辨率可以提高模拟正确率、更准确模拟波导特征参数，其次是SST的更新周期，在一定程度上能改进模拟结果；

3)在最优的SST驱动下，子网格提高了模拟正确率和发生概率，降低了虚报率和波导强度、厚度误差，但在波导底高上优势不明显.

上述结论对南海低空大气波导数值预报具有重要的科学意义和应用价值.