全封闭设备舱对隧道内160km/h地铁气动声源影响
杨志刚,高建勇,谭晓明,余永革,刘慧芳,吴雨薇
(1.中南大学 交通运输工程学院 轨道交通安全教育部重点实验室,长沙 410075;2.合肥工业大学 汽车与交通运输工程学院,合肥 230009;3.长春轨道客车股份有限公司 铁路客车开发部,长春 130062)
近年来,我国城市轨道交通系统发展迅速,新一代地铁列车运行速度由80 km/h 提升至120 km/h~160 km/h区间。由于气动噪声与车速呈现6倍以上指数关系,速度的倍增将显著增加车外气动激励噪声和车内噪声。线路试验表明,地铁列车在隧道内160 km/h 运行时,车内噪声水平较明线增加了11.2 dB(A)~18.7 dB(A)[1],会严重降低乘客乘坐舒适度。地铁列车气动噪声问题已经成为发展新一代地铁列车的关键问题之一。
地铁列车的气动/声学问题有其特殊性。高速列车隧道线路阻塞比一般在0.12~0.14,高速列车在300 km/h 时,列车表面声源能量是明线的3 倍左右[2-3],车内噪声强度增加5 dB~10 dB。而地铁线路阻塞比远大于高速列车,在0.5 左右,同等速度级下地铁列车周围流场受到隧道壁面影响明显更强。因此,尽管160 km/h速度并不高,但其气动激励效应已不容忽视。且一般而言,增加头车流线型长度能较好的改善列车气动性能[4-5]。而地铁列车由于司机室视野和载客量要求[6],车头多为钝形或短流线型[7-9]。这进一步增强了车体的气动激扰效应。
传统地铁运行速度低,结构复杂的车下设备直接挂装在车底。列车以160 km/h 运行时,裸露的车底设备会成为流场恶化的主因。已有研究表明,车体底部气动激扰是车内噪声的主要来源之一[10]。朱剑月等[11]利用延迟分离涡模型和FW-H 方程研究了由轮对、轴和框架组成的简单转向架的流场和气动噪声特性,发现峰值噪声来自车轴,车架对总噪声的贡献率低于轮对。Latorre等[12]和Yamazaki等[13]的研究表明:上游转向架区域的气动噪声大于下游转向架区域的气动噪声,转向架舱后缘的噪声大于前缘的噪声;具有弧形前缘和侧裙板的转向架腔可有效降低自身产生的气动噪声。
到目前为止,针对地铁列车气动噪声优化的公开文献研究较少。本文尝试针对车底气动激扰的焦点问题,采用全封闭设备舱疏导底部流场,采用LES(Large Eddy Simulation)方法数值研究全封闭设备舱设计对隧道内160 km/h地铁列车气动噪声的影响规律,这能够为我国新一代地铁噪声控制提供技术参考。
1 数值计算模型
1.1 几何模型及计算域
如图1所示,本文所用模型为4 车编组、带转向架、无受电弓的1:8 缩比地铁列车模型;从上游至下游,四节车分别为头车、中车1、中车2 与尾车,每节车分为车体上部与车体底部;模型分为无设备舱设计模型和全封闭设备舱设计模型(其区别仅在于车底设备封装形式)。全尺寸列车长约94 m,高约3.5 m。在160 km/h 时,以车高为特征长度计算的雷诺数约为1.34×106。

图1 列车模型图
全尺寸计算域如图2所示,列车车轮最低点距离地面0.2 m。隧道计算域全长894 m,车头鼻尖距离隧道入口300 m,尾车鼻尖距离隧道出口500 m。采用B型地铁列车矩形隧道截面,截面面积为17.46 m2,无设备舱和全封闭设备舱列车的隧道阻塞比分别为0.44和0.50。

图2 全尺寸计算域示意图
1.2 计算方法和边界条件
采用可压缩理想气体。列车壁面设置为固定壁面;地面和隧道壁面定义为滑移壁面,滑移速度与来流速度一致;为消除出口和入口压力波反射对声场的影响,将计算域入口和出口分别设置为压力远场入口和压力出口,压力出口设置为声学无反射边界条件[3,14]。
计算分为稳态与瞬态计算两部分。稳态计算基于压力基隐式求解方法。湍流模型选用SST-kω模型,近壁面选用加强壁面函数。选用压力-速度耦合的SIMPLE算法,压力采用Standard离散格式,动量、湍动能、湍动能耗散率采用2 阶迎风离散格式。瞬态计算的湍流模型选用LES,亚格子模型为Smagorinsky 模型,选用压力-速度耦合的COUPLE 算法[3,14-15]。
本文瞬态计算的时间步长取5×10-5s,每个时间步长内迭代30 步,共计算10 000 个时间步,共计0.5秒,以保证列车周围流场充分发展。
1.3 网格划分方法
采用ICEM划分网格,车体表面为三角形网格,空间为四面体网格,设置内外嵌套的三层加密区,从内到外全尺寸空间网格分别为100 mm、250 mm 和500 mm。头车/尾车面网格尺度为40 mm,中车面网格尺度为50 mm。列车表面附面层为三棱柱网格,第一层网格高度为0.1 mm,增长率为1.2,共15 层;壁面及地面附面层第一层网格高度均为5 mm,增长率为1.2,共8 层。全封闭设备舱和无设备舱的列车模型网格规模分别为8 100万、7 700万。图3为局部网格切片图。

图3 局部网格切片图(全尺寸,计算时采用1:8缩比)
时间步长对应的最高分析频率为10 kHz,但根据第一层加密区空间网格尺度,本文分析频率最高约为4 500 Hz;考虑到列车的主要声源能量一般在4 kHz以下[3,16],本文的分析频率上限取4 kHz。
为验证网格无关性,调整三层加密区网格尺寸得到粗网格和细网格列车模型,如表1所示,网格量分别为5 233万和9 334万。三套网格得到的稳态气动阻力系数分别为2.14、2.10、2.11,计算网格和细网格整车阻力系数之间的偏差小于3%,可认为本文计算网格模型满足网格无关性要求。

表1 网格模型数据(全尺寸/mm)
瞬态计算要求空间网格尺度处于当地惯性子区,即空间网格尺度要小于当地积分尺度[2]。图4给出模型的网格参数图,可见在所有区域网格参数都在1以下,证明本文网格能满足LES模型计算要求。

图4 网格参数
本文网格划分方法、湍流模型和边界条件等已在文献[2]完成校核。校核模型仿真结果和风洞试验[17]结果吻合。详细校核过程见附录。
2 结果与分析
2.1 无设备舱列车脉动激扰流场结构
图5给出无设备舱列车空间Q判据辨识的三维涡结构云图,采用速度幅值着色。整体而言,相对明线,车体周围的气动激励加剧。无设备舱模型脉动激扰流场结构具有以下特征:
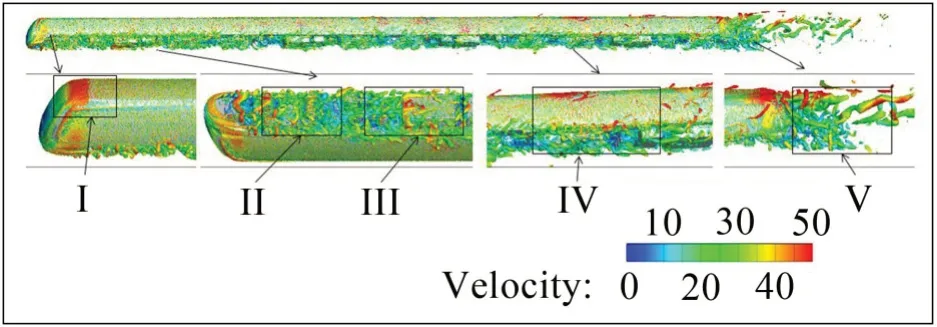
图5 无设备舱Q=200 000/s2等值面空间涡结构云图
(1)车体、尤其是顶部的气流加速效应增强。小尺度涡结构I沿车顶向后发展,并在后部出现了明显的分离再附现象。
(2)头车排障器底部的周期性脱落涡受头车一位转向架阻挡,部分涡结构向两侧发展成单脚发夹涡;另一部分涡结构在转向架部位破碎形成较丰富尺度的混合型脱落涡II;涡结构II向下游发展,在车底设备周围破碎、掺混,形成不同尺度的涡结构III。
(3)转向架区域溢出流向后上方发展,扰动逐渐贴近车体侧面,并在尾部和车顶高速气流部分掺混IV。
(4)在尾车及尾流区,车顶高速气流、两侧泄露气流以及车底气流强烈掺混,形成相对明线时更强的大尺度尾涡结构区V。
底部设备舱区域的调整能够直接或间接影响这5个近壁面的主要气动激扰特征,进而改变列车气动噪声源特征。
2.2 全封闭设备舱对流场结构的影响
图6给出了全封闭设备舱三维涡结构云图,该图和图5采用相同的色度条着色。
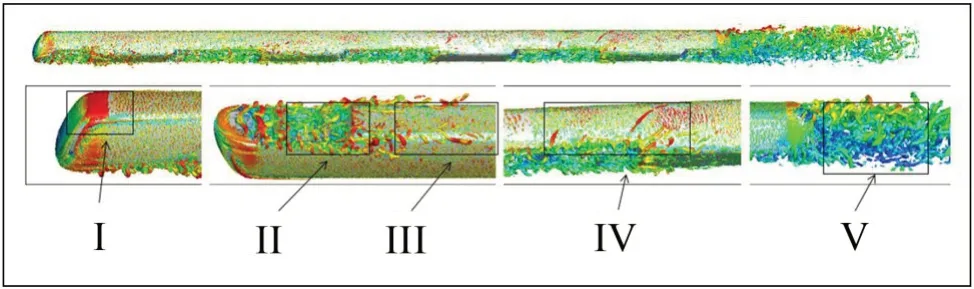
图6 全封闭设备舱Q=200 000 s2空间涡结构云图
由图可见,全封闭设备舱设计增强了隧道阻塞效应,使得列车周围气流速度不同程度的增加,车顶区(I)、车底区(II、III)及尾流区(V)的气流速度分别增加约12.8%、7.9%、8.3%、19.0%。车顶区和尾流区的涡量强度得到较大幅度增加,I区和V区涡量强度分别增加了78.4%和82.2%;而较多抑制了车底设备区域的低速强涡量区域,车底区II和III的涡量强度分别减小15.5%和27.4%。迫使列车底部相对低速扰流结构更多的集中在转向架舱溢出并向车顶发展、部分掺混,导致车体侧面区IV 的涡量强度和气流速度均有小幅减小,分别约4.9%和7.0%。
从涡结构尺度来看,区域I的涡结构主尺度几乎无改变;全封闭设备舱使得车底的扰动结构尺度变大,II区和III区分别增大了20%和36%,进而影响车体侧面的扰动结构尺度也增大了37%;区域V,由于车顶高速气流和车底低速气流的剧烈掺混,导致主要涡结构尺度减小50%。列车周围流动变化的具体数据如表2所示。

表2 列车流场结构变化(相对于无设备舱模型)/(%)
其中“—”表示变化可忽略不计。应该注意到,涡结构运动形态和气动噪声源的能量分布及谱型特征关系密切。下文对列车声源能量强度和频谱变化进行分析。
2.3 全封闭设备舱对列车等效声源能量强度的影响
对于噪声源,可通过等效声源声功率表示其强度变化,其计算公式可通过Curl积分方程推导,推到过程见文献[15],这里仅给出等效声源声功率计算公式:

其中:p是高速列车表面脉动压力,可以理解为声源声强,“—”表示时域平均值,S为声源面积。该公式表明,列车表面脉动压力的时间变化率值p′rms可以反映列车表面声源能量强度。
地铁列车表面脉动压力对应的偶极子气动噪声源是车内气动噪声的主要来源。这里不讨论次一级的隧道壁面以及尾流区的激扰、掺混噪声,也不讨论隧道的混响效应(这是传播效应)。图7给出采取全封闭设备舱后各列车部件等效声源能量相对于无设备舱列车整车等效声源能量的变化情况,对应数据见表3所示。具体如下:

表3 各部件声源能量变化/(%)

图7 车体表面脉动压力时间变化率均方根p′rms分布云图(隧道)
(1)对车体上部,声源能量高的区域集中在转向架舱下游,而中车2 和尾车顶部和两侧的高声源能量区域减少;对应的,头车和中车1的等效声源能量分别增加约13.2%和9.4%;而中车2上部和尾车上部的等效声源能量分别减小约3.3%和12.0%,整车车体上部的等效声能量增加7.3%。
(2)对于车底部件,由于车底设备被包裹,车底声源能量强度高的区域减少,集中在设备舱上游和转向架部位。车体底部部件声源能量减小,头车、中车1、中车2和尾车等效声源能量分别减小约7.5%、0.1%、0.9%和1.8%,整车减小10.3%。
(3)对于各节车厢,即将车体上部和车体底部综合考虑:头车、中车1分别增大5.7%和9.3%,中车2和尾车分别减小4.2%和13.8%,表明各节车体声源能量分布更加均匀。
(4)对于整车:声源能量减小约3.0%。
2.4 全封闭设备舱对声源频谱的影响
对列车表面脉动压力时间变化率进行傅里叶变换,应用公式(1),得到列车不同频率的等效声源声功率值。这里仅展示列车整车、头车车底和尾车上部的频谱能量占比特征变化,如图8和图9所示。
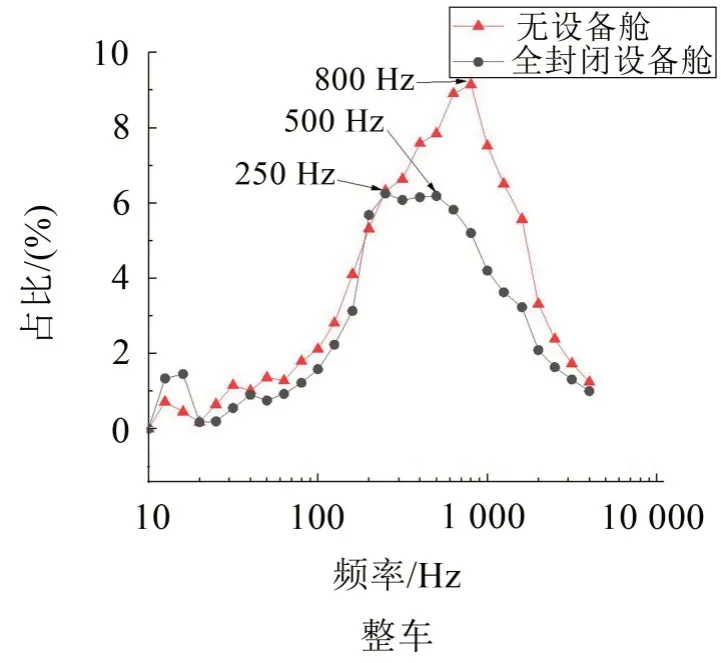
图8 整车等效声源声功率频谱曲线(1/3倍频程)

图9 列车部件等效声源声功率频率图(1/3倍频程)
图中的百分比数据为采用全封闭设备舱的整车或各部件的各频段等效声源声功率与原型车等效声源声功率的百分比值。
等效声源声功率频谱变化如下:
(1)无设备舱整车、头车车底和尾车上部均具有明显的单峰值特性,峰值频率均为800 Hz,采用全封闭设备舱后800 Hz峰值频率能量被削弱,其峰值频率分别变为250 Hz~500 Hz、400 Hz和630 Hz。
(2)整车:全封闭设备舱使400 Hz~2 000 Hz 频率段内等效声源能量减小幅度超过1%,峰值频率声源能量减小约4.0%;并出现250 Hz 和500 Hz 两个峰值频率,且250 Hz~500 Hz 频率段等效声源能量相差不大。
(3)头车车底:全封闭设备舱对涡结构III的抑制是各频段等效声源能量减小的主要原因;250 Hz~1 600 Hz频段的等效声源能量减小幅度超过1%,峰值频率声源能量减小约2.4%。
(4)尾车上部:该部位主要受车底气流和尾流区共同作用影响,车底气流主要影响尾车两侧声源能量,尾流主要影响尾车流线型区声源能量。无设备舱模型车底激扰气流漫过尾车车顶,主导尾车上部频谱特征。采用全封闭设备舱后,一方面,车底激扰气流主要涡结构尺度变大,引起尾车上部两侧高频等效声源能量减小,另一方面,尾流区气流对流线型区的影响增强,而尾流区掺混气流的主要涡结构尺度较车底主要涡结构尺度大,使得低频声源能量相对增强。尾车上部630 Hz~1 250 Hz的等效声源能量减小幅度超过1 %,峰值频率声源能量减小约1.8%。
3 结语
本文利用大涡模拟,对无限长隧道内1:8缩比地铁列车模型的气动噪声源进行数值模拟,研究全封闭设备舱对列车本体气动噪声源的影响。全封闭设备舱通过疏导车底流场减小列车底部气动声源能量;但同时增加了阻塞比,并使车底激扰气流集中在转向架舱两侧溢出,增加车体上部声源能量。全封闭设备舱设计对流场和气动噪声源的影响如下:
(1)列车周围气流速度增加,而涡量强度得到抑制,除尾流区外主要涡结构尺度增大。在对车体声源能量影响最大的车底区域,头车一位转向架、设备舱底部区域气流速度分别增加7.9%和8.3%;涡量强度分别减小15.5%和27.4%;主要涡结构尺度分别增大20%和36%。
(2)在车体上部,头车和中车1受车底激扰气流影响增强,声源能量增加13.2%和9.4%;中车2 和尾车受车底气流影响减弱,声源能量分别减小3.3%和12.0%。车体底部部件声源能量则不同程度的减小,减小程度最大的是头车车底,约7.5%。
(3)将车体上部和车体底部综合考虑:头车、中车1分别增大5.7%和9.3%,中车2和尾车分别减小4.2 %和13.8 %,表明各节车体声源能量分布更加均匀。
(4)无设备舱整车、头车车底和尾车上部峰值频率均为800 Hz,采用全封闭设备舱后峰值频率分别为250 Hz~500 Hz、400 Hz和630 Hz,并且列车高频声源能量减小,如整车、头车车底和尾车上部的峰值频率声源能量分别减小4.0%、2.4%和1.8%。
附录:
在某声学风洞进行高速列车气动噪声试验。试验模型为1:8 缩比的三车编组模型。列车模型安装在长11.72 m,宽0.9 m,高0.06 m的路基上。在试验模型一侧,安装30 个远场传声器。图1为试验现场图,图2给出了远场传声器位置。

图1 声学风洞试验现场图

图2 远场传声器安装位置
采用与和本文相同的网格划分策略和湍流模型,数值模拟风洞试验中高速列车周围的流场扰动,并利用FW-H 方程预测高速列车的远场辐射噪声。对30 个远场传声器的噪声结果[17],与仿真结果进行对比,其频谱结果对比绘制于图3中。
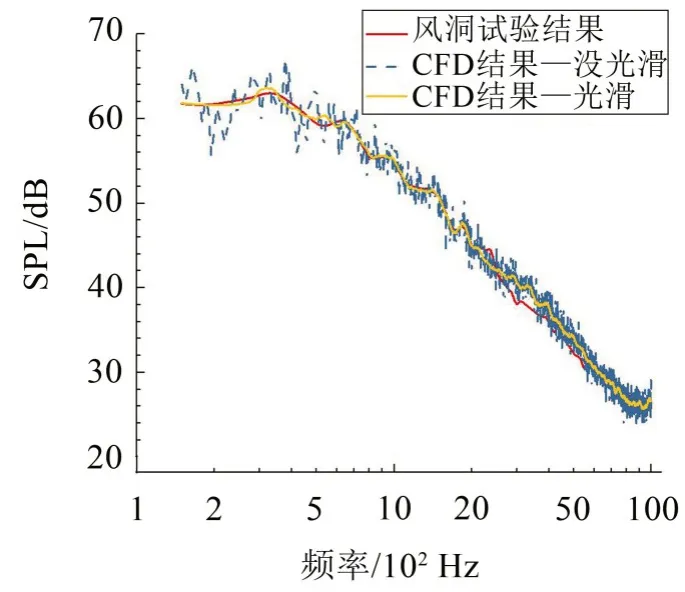
图3 仿真结果与声学风洞试验结果对比图(来流速度55.56 m/s)
对比结果表明,试验和仿真数据变化趋同,在2 kHz 以下结果吻合良好,在2 kHz 以上吻合稍差,但差值在2 dB以内。这表明本文采用的湍流模型、网格划分策略符合精细化数值仿真要求,能用于地铁本体气动噪声源的研究。

