基于简化模型的Y型偏心支撑钢框架滞回性能分析

段文峰，曹晓娇，刘文渊

1吉林建筑大学 土木工程学院,长春 130118;2南京理工大学泰州科技学院,江苏 泰州 225300

0 引言

偏心支撑钢框架由框架柱、框架梁、斜向支撑及耗能梁段4个部分组成.该结构体系将抗弯钢框架及中心支撑框架两者的优点有机结合，偏心支撑结构在弹性范围内刚度很大,能够满足结构侧移要求,是适用于高烈度地震地区的一种有效的结构体系[1-2].在地震发生时,耗能梁段先屈服,通过塑性变形消耗能量,从而达到保护主体的作用.

于安林、赵宝成等[3]人对K型和Y型偏心支撑钢框架结构进行低周往复荷载试验.结果表明,K型和Y型偏心结构在小震或中震作用下满足结构变形要求,同时在大震作用下可以提供良好的变形能力和耗散地震能量的双重功能.舒伟伟等[4]人为了研究高强钢组合Y型偏心支撑框架的滞回性能,运用 ABAQUS软件建立了单层单跨结构的壳单元模型,对有限元模型进行循环加载分析.Tian X等[5]人为了研究3层K型偏心支撑的抗震性能,使用ANSYS软件建立实体单元结构模型.刘文渊等[6]人将传统偏心支撑中耗能梁段制作材料更换为形状记忆合金,并采用ANSYS软件建立精细化全实体有限元模型进行滞回性能分析,发现结构具有较好的自复位性能.为评估SMA耗能梁自复位偏心支撑钢框架的抗震性能,刘文渊[7]等采用ANSYS有限元软件建立多尺度有限元模型进行地震时程分析，梁、柱及支撑采用BEAM188梁单元,耗能梁采用SOLID185实体单元,梁单元与实体单元连接处自由度不协调问题,梁单元与实体单元之间通过MPC算法实现点-面接触来对新型自复位钢框架.刘美子[8]运用 ABAQUS 有限元软件中建立K型偏心支撑结构的梁壳混合单元模型,进行数值模型并对结构抗地震倒塌分析.苏明周等[9-10]人为进一步研究高强钢组合Y型偏心支撑框架结构的抗震性能,将1∶2缩尺的Y型偏心支撑结构模型试件进行振动台试验.在结构恢复力模型及等代拉杆模型的基础上,把耗能梁和支撑简化为斜向杆件,利用SAP2000程序中的多线段塑性Kinematic代替杆件.随后,又以一个3层3跨的高强钢组合Y型偏心支撑框架结构为例,采用子结构混合试验方法进行试验研究,并运用OpenSees有限元软件进行模拟.

关于偏心支撑滞回性能研究方面的试验及有限元成果较为丰硕.已有的有限元研究成果主要集中在采用全实体、全壳、杆件与实体或壳混凝土单元对该类结构进行滞回性能模拟,模拟中易出现收敛性问题及复杂接触问题(不同自由度的单元连接问题)，且采用该类模型进行高层建筑地震时程分析时问题更为突出.将耗能段简化为杆件单元并考虑耗能梁腹板剪切变形的影响，使计算更为便捷，这是解决此类问题的关键.因此，本文尝试采用钢板剪力墙的统一等代模型对剪切型耗能梁段腹板进行简化,建立偏心支撑钢框架结构的全杆件模型,既解决了不收敛问题,又提高了建模速度,为后续研究结构的层剪力分布模式做铺垫.研究时对已有试验的耗能段进行简化模型的有限元分析,并与试验结果进行比较,进一步验证简化模型的正确性及可靠性.

1 耗能梁的分类及简化

1.1 耗能梁的分类

耗能梁可分为剪切屈服型、弯曲屈服型及弯剪屈服型,一般通过耗能梁长度系数ρ来划分[11]：

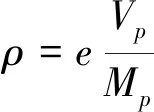
(1)

式中,e为耗能梁长度,m；Vp为腹板塑性抗剪承载力,kN;Mp为耗能梁塑性抗弯承载力,kN·m.当ρ≤1.6时,耗能梁为剪切屈服型;当ρ≥2.6时,耗能梁为弯曲屈服型;当1.6≤ρ≤2.6时,耗能梁为弯剪屈服型.

1.2 钢板剪力墙的统一等代模型

剪切型耗能梁腹板可按钢板剪力墙的统一等代模型进行简化.钢板剪力墙的力学性能一般由高厚比λn来控制,按高厚比不同可分为3类[12]：当λn≤0.8时,钢板墙的剪切屈服不先于全截面剪切屈服,属于厚板范畴;当0.8<λn≤1.2时,钢板墙剪切屈曲发生在弹塑性阶段,归为中厚板;当λn>1.2时,钢板墙在弹性范围发生剪切屈曲,归为薄板范围.

由于传统等代模型不能用于任意厚度的钢板墙，郭彦林等[13]人提出统一等代模型,该模型可用于任意厚度钢板墙的简化,且具有较高的精度.

当为厚板时,墙板表现为“完全剪切机制”的受力特征,钢板墙全截面受剪屈服,墙板可替换成倾斜正交的“拉压同性”杆件.

当为薄板时,墙板表现为“完全拉力场机制”的受力特征,钢板墙受拉屈服,墙板等效倾斜正交“只拉不压”杆件.

当为中厚板时,表现出厚板与薄板之间的特性,此时钢板墙的受力特征为“完全剪切机制”和“完全拉力场机制”在某一比例下的组合.

统一等代模型中将杆件截面积分为:剪切作用部分面积和拉力场部分面积,分别用式(2)，式(3)表示:

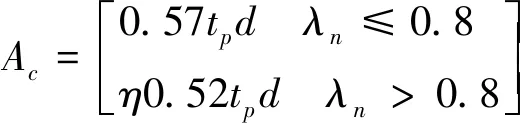
(2)

As=(1-η)tpd

(3)

式中,tp为墙板厚度,mm;d为从属宽度,mm;η为剪切作用部分比例,用式(4)表示:

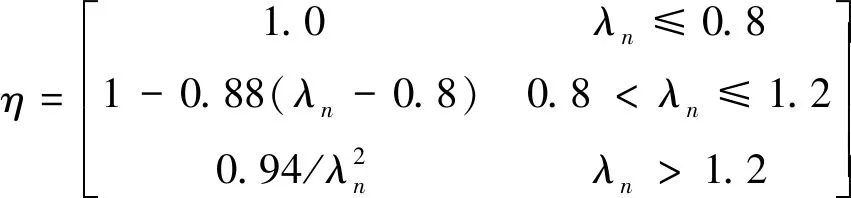
(4)

1.3 耗能梁的简化

在有限元模拟中,由于耗能梁模型构建比较复杂耗时及不收敛等一系列问题,故本文将钢板剪力墙的统一等代模型用于剪切型耗能梁腹板中,在有限元模拟时把耗能梁腹板等效简化成杆件单元.通过上述板的类型及其统一等代模型的简化,对于腹板λn≤0.8的耗能梁,此时耗能梁的受力特征为“完全剪切”机制,但由于耗能梁尺寸较小,以加劲肋为界,把腹板进行区域划分,分别简化为两根“拉压同性”的杆件单元.

2 试验验证

为验证简化模型的正确性,采用SeismoStruct有限元软件建立高强组合单层单跨Y型偏心支撑结构滞回性能试验[14]的简化数值模型,并进行往复加载,研究其滞回性能.

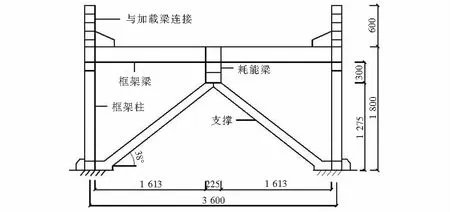
图1 试件尺寸(单位：mm)Fig.1 Specimen size(Units：mm)

2.1 试验介绍

焦培培[14]对1∶2缩尺的高强组合单层单跨Y型偏心支撑钢框架进行低周往复加载试验,且耗能梁设计成剪切型,梁与柱、梁与梁、支撑与梁、支撑与柱均采用焊接连接,柱与基础梁采用高强螺栓连接,加劲肋位于耗能梁中间位置.框架层高为1.8 m,跨度为3.6 m,框架梁、框架柱、支撑均采用Q460C钢,耗能梁采用Q345B钢,试件尺寸如图1所示,框架柱、框架梁、耗能梁段及支撑构件截面尺寸见表1.材料弹性模量、屈服强度、极限抗拉强度、伸长率及泊松比见表2.

表1 Y型偏心支撑框架试验模型构件Table 1 Y-type eccentrically braced frame test model components

表2 钢材的力学性能参数Table 2 The mechanical property parameters of steel

2.2 有限元模型

本文采用通用有限元程序SeismoStruct Y型偏心支撑结构的滞回性能进行了pushover分析.SeismoStruct是一款能够对静态或动态载荷作用下结构可同时考虑几何非线性和材料非线性的通用有限元程序.单元类型选用Inelastic force-based plastic hinge frame element(简称:infrmFBPH)单元,各杆件单元分别被划分为6个infrmFBPH单元,截面纤维数均取150个.钢材本构选用软件中自带的Bilinear steel model (简称:stl-bl)模型来模拟其力学性能,此模型为双线性弹塑性硬化模型,钢材屈服强度见表2,屈服后切线模量取0.005E,采用 Mises 屈服准则进行屈服判定.建立Y型偏心支撑结构等效的杆件模型.在有限元模型中,对钢柱底部施加固定约束;钢梁与钢柱刚接;耗能梁段所有杆件单元之间均为铰接;支撑杆件与耗能梁、钢柱底部均为刚接,如图2(a)所示.

基于钢板剪力墙的统一等代模型理论,将耗能梁的腹板等效简化为杆件单元,建立全杆件模型.耗能梁段腹板尺寸150 mm×205 mm,板件厚度为6 mm,属于厚板的范畴,此时耗能梁腹板的受力特征与厚钢板剪力墙的受力特征相同,均为“完全剪切机制”,tp=6 mm,d=254 mm,根据公式(2),确定杆件截面面积Ac=868.68 mm2,将耗能梁腹板简化成矩型截面,其尺寸为29.47 mm×29.47 mm.有限元模型如图2(b)所示.腹板四周杆为刚性杆,其尺寸与耗能梁翼缘的尺寸相同(刚性杆截面尺寸对试件分析几乎无影响).

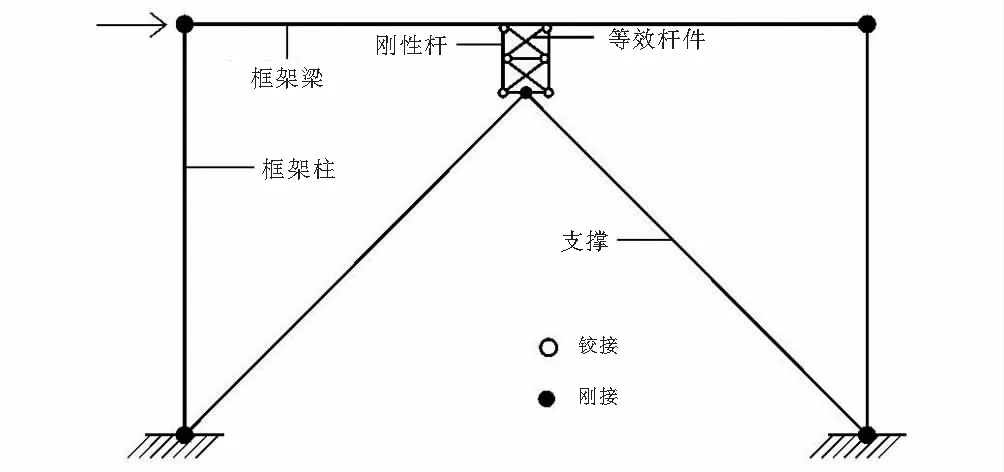
(a) 模型简图

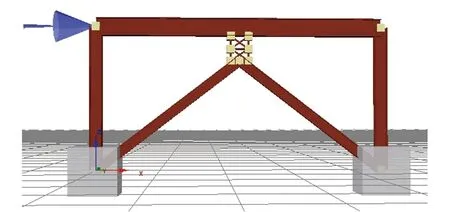
(b) 有限元模型

2.3 加载制度

在有限元模拟的过程中对试验的加载制度进行了简化,加载方式采用位移控制，其目标位移分别为9 mm(Δ),18 mm(2Δ),27 mm(3Δ)，…n×Δ.每级荷载循环1次.

3 试验与有限元对比

3.1 滞回曲线

图3给出了试件的试验与模拟的对比滞回曲线,试验的滞回曲线与有限元的曲线大致吻合.试验曲线和模拟曲线形状接近,均呈纺锤状,曲线饱满、无明显的捏缩现象,试验加载到最大位移时结构的承载力为661.3 kN,而有限元模拟值为650.6 kN,试验值与有限元模拟值差异较小(两者相差约为1.64 %).

3.2 骨架曲线

骨架曲线是滞回曲线上同向各级加载中荷载极值点依次相连得到的包络图,能够直观地反应试件的强度、刚度、耗能能力等特征.图4给出试件的试验与有限元模拟的对比骨架曲线.由图4可以看出,试验和有限元模拟的骨架曲线基本吻合.试验和有限元模拟的骨架曲线在层间位移角达0.5 %之前增长较快;层间位移角到0.5 %后增长缓慢,都趋于平缓状态,曲线未出现下降段,且试验值略低于模拟值(最大差异在4 %以内).总体来说,试验与有限元模拟的骨架曲线吻合较好,试件的有限元模拟骨架曲线能够较好的反映试验,进一步说明了有限元模拟的正确性.

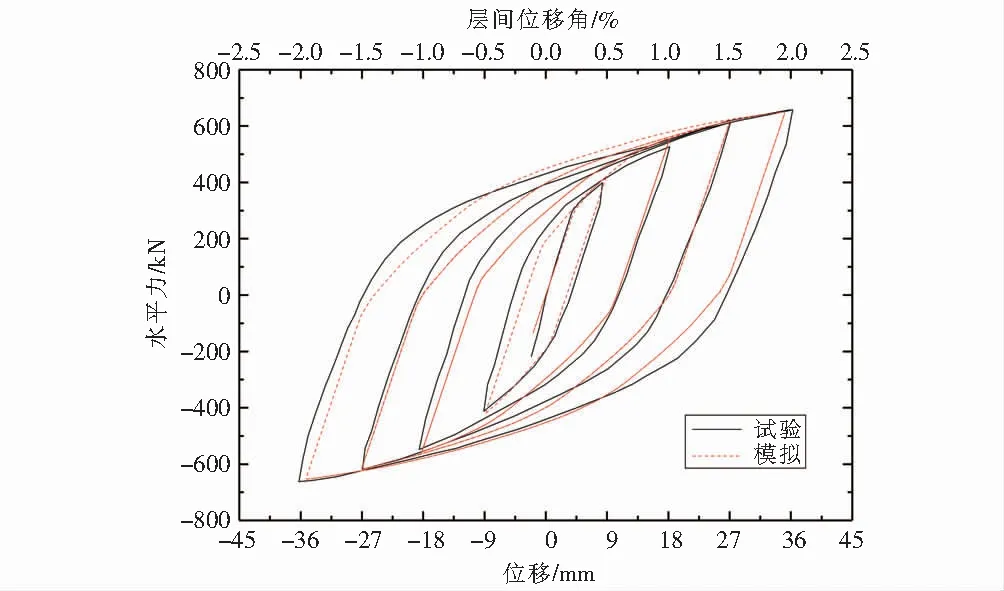
图3 滞回曲线Fig.3 Hysteretic curves

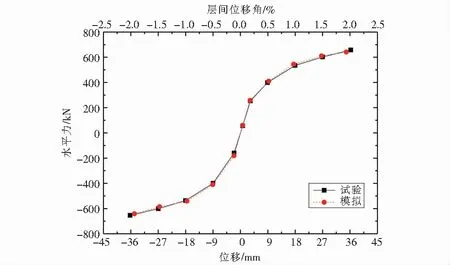
图4 骨架曲线Fig.4 Skeleton curves

3.3 刚度退化

割线刚度能够反映试件在加载过程中刚度退化规律,割线刚度K可按下式(5)计算：

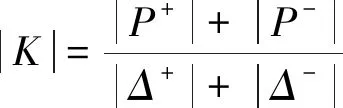
(5)

式中,P+,P-为同一滞回环内的正、负向顶点荷载,kN;Δ+,Δ-为同一滞回环内的正、负向顶点位移,mm.

图5给出试件加载过程中试验与有限元模拟的刚度退化对比曲线.由图5可以看出,试验得出的初始刚度为71.9 kN/mm,有限元模拟的初始刚度值为63.7 kN/mm,两者相差6.9 %;最后一圈加载时,试验与有限元模拟的刚度都退化至约18 kN/mm;层间位移角在1 %之前抗侧刚度曲线下降较快,在1 %之后抗侧刚度曲线下降较为平缓.因此,试验与有限元模拟得到的曲线吻合较好,有限元模拟能够较好的反映试验状况,进一步说明了有限元模拟的可靠性.

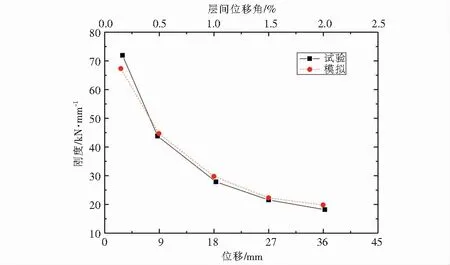
图5 刚度退化曲线Fig.5 Stiffness degradation curves

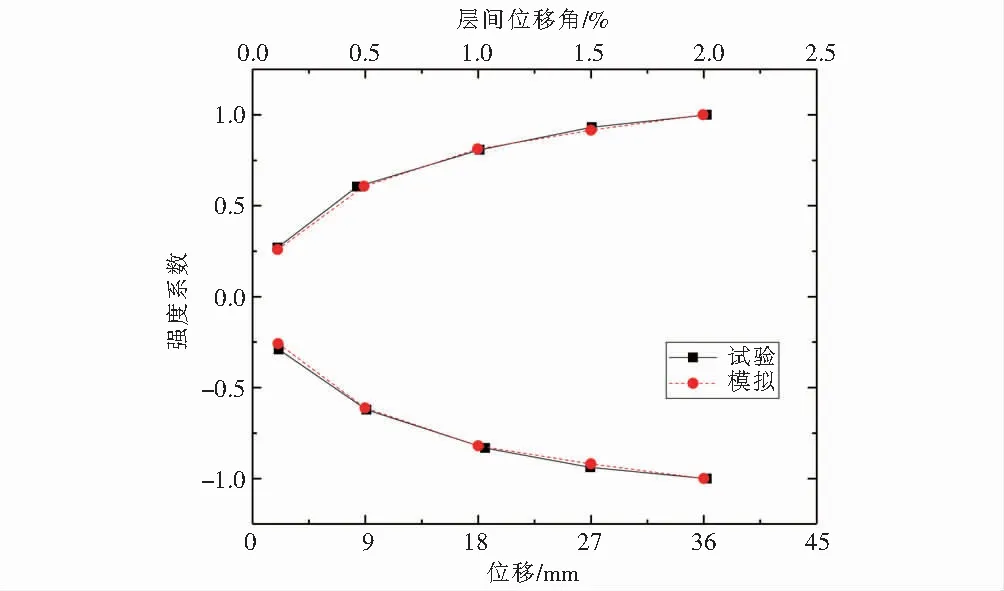
图6 强度退化曲线Fig.6 Strength degradation curves

3.4 强度退化

强度退化曲线能够直观地反应结构的受损程度及规律,为更好地观察随荷载增加试件的强度退化情况,引入整体强度系数λj,λj为试件在j级荷载下第1次循环的荷载峰值与试件整个加载过程中的最大荷载的比值,可按式(6)计算：

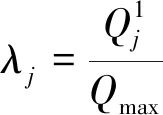
(6)

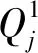
图6给出试件在异级荷载作用下试验与有限元模拟的强度退化曲线的对比.试件的初始强度系数大约在0.25左右,加载到最后一圈时,强度系数在1.0左右;层间位移角在1 %之前刚度退化较快,在1 %之后强度退化曲线较为平缓.总体来说,试验与模拟的强度退化曲线吻合良好,简化规则能够较好地反应剪切型高强钢组合Y型偏心结构的刚度退化规律.

3.5 耗能能力

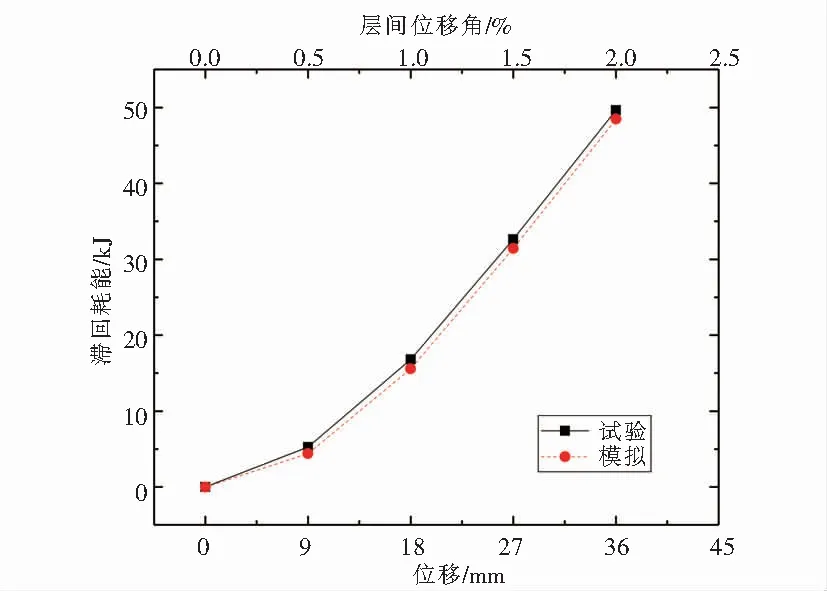
图7 耗能能力Fig.7 Energy dissipation capacity

耗能能力是衡量结构抗震性能的主要指标之一,曲线包围的面积越大,说明结构的耗能能力越强.图7给出试件加载过程中试验与有限元模拟的能量耗散对比曲线.由于试件的滞回曲线呈饱和的“纺锤体”型,所以试件的耗能能力较强.由图7中可以看出,试验与有限元模拟的结果大致相同,实验值略高于模拟值,均呈现上升的趋势.当层间位移角达到0.5 %时,试验与有限元模拟耗能能力相差最大,试验的滞回耗能为5.263 kJ，有限元模拟的滞回耗能为4.386 kJ,相差约为20 %.当层间位移角达到2 %,试验和有限元模拟的滞回耗能均达到48 kJ以上.综上所述,剪切型高强钢组合Y型偏心支撑框架耗能能力较强.

4 结论

基于钢板剪力墙统一等代模型理论,对耗能梁进行等效，并将简化模型用于对高强钢组合Y型偏心钢框架的滞回性能进行数值模拟,模型采用通过有限元SeismoStruct软件建立.将简化模型分析结果与试验值进行对比,得到以下结论:

(1) 基于钢板剪力墙的统一等代模型理论,对剪切型耗能梁腹板等效简化为交叉杆件单元,并对整体结构进行滞回分析,验证了Y型偏心支撑钢框架结构的全杆件单元模型具有较好的可行性.

(2) 数值分析得出的滞回曲线、骨架曲线、刚度退化、强度退化与耗能能力均与试验值吻合较好,验证了有限元模型的可靠性.

(3) 通过有限元SeismoStruct软件建立杆件单元模型计算速度较快,且分析过程中未出现收敛性问题.该模型可用于后续开展复杂偏心支撑钢框架结构的地震时程分析.