中美经贸摩擦与制造业股票的系统性风险——基于随机矩阵理论的实证研究

黄春敏 刘桂荣

（华东理工大学商学院 上海市 200237）

一、引言及文献综述

2018 年3 月23 日，美国对中国600 亿美元商品加征25%的关税，拉开了中美经贸摩擦的序幕。国际货币基金组织的2018 年度报告指出，中美经贸摩擦将造成中国金融市场动荡。众多学者密切关注着经贸摩擦对中国金融市场的影响，并进行了一系列研究。有学者认为经贸摩擦降低了中国股市收益率且加剧了股市波动（吕频捷和顾艳伟，2020；陈奉功和张谊浩，2021；杨平，2020）。赵军产等（2021）利用2016-2019 年上证行业指数构建格兰杰因果网络，分析经贸摩擦对中国上证103 个行业的冲击。研究结果显示，上证行业的金融风险传播在经贸摩擦发生初期更快。Yanshuang Li 等（2020）基于复杂网络理论，分析经贸摩擦对中国股市的影响。结果表明，经贸摩擦对中国股市各个板块的风险溢出效应有显著影响。尹志超等（2020）采用事件研究法，研究表明经贸摩擦的负面事件比正面事件对中国股市的影响时间更长。张峥（2019）采用事件研究法分析经贸摩擦对中国制造业股价的影响，研究表明市场对中美经贸摩擦表现出消极态度，多数人认为中国制造业前景堪忧。除此之外，还有一部分学者对经贸摩擦前景呈乐观态度。黄纯辉（2018）和龚婷（2018）都认为贸易战对制造业的负面影响是短期的，长期来看，经贸摩擦有助于提升中国制造业的创新能力和促进产业转型。

关于经贸摩擦对中国股市影响的研究，学者多从价格收益率和风险传播的角度入手，鲜有关注经贸摩擦对中国股票相关性结构特征影响的定量研究。经贸摩擦的焦点以中国高端制造业产品为主，经贸摩擦必将影响中国制造业相关产品的生产和出口，引发制造业上市公司股价的变动。与现有关于经贸摩擦对中国制造业影响的事件研究法不同，本文运用随机矩阵理论（Random Matrix Theory，RMT）实证分析经贸摩擦对中国制造业股票相关性结构的影响，着重比较原始相关矩阵和偏相关矩阵之间的特征值偏差和特征向量偏差所含的信息，揭示经贸摩擦对制造业股票系统风险的影响。

股市是一个非常复杂的经济系统，股票收益相关性是股票市场的基本规律。根据马科维茨的均值-方差模型，运用相关矩阵进行金融风险管理具有普遍性。然而，Ang 和Chen（2002）的分析指出，市场信息会对股票的相关性结构产生显著影响。如，在经济冲击产生时，股票间的相关性提升（谢邦昌和游涛，2015；马丹等，2016）。市场相关性结构的时变性、股票市场的非平稳性以及样本时间跨度有限等问题，导致基于市场数据构建的相关矩阵很大程度存在“噪声”。因此在进行投资决策时，不能盲目使用马科维茨最优投资组合理论（Laloux 等，1999）。“噪声”的存在会干扰最优投资组合的获得，误导金融决策。为解决上述问题，进行有效的投资风险估算，可以借助随机矩阵理论，通过比较真实收益相关矩阵和随机相关矩阵的统计特性，区分股票价格相关性的“噪声”和真实信息部分。

随机矩阵理论是处理高维数据的有效方法，由数学物理学家Wigner 在1951 年研究复杂原子系统能级的统计特性时首次提出。随机矩阵理论自提出就被广泛应用于信号处理、地震预测、股票市场分析等多方面。金融体系中存在大量复杂的数据，这是RMT应用于金融市场的基础。1999 年，随机矩阵理论被首次应用于金融市场的相关性分析。二十多年来，学者们已经将随机矩阵理论广泛应用于成熟金融市场（Laloux 等，1999；Plerou 等，1999；Plerou 等，2002；Utsugi 等，2004）和新兴市场（Kulkarni 和Deo，2007；Namaki 等，2011；Oh 等，2011；Han 等，2017），并得出具有普遍适用性的结论。例如，影响股票收益率的真实信息蕴藏在偏离RMT 预测范围的特征值和特征向量中（Laloux 等，1999；Plerou 等，2002）。部分文献通过偏离特征值分析股票相关性结构的动态演变（Hao 等，2014；Ren 和Zhou，2014），另有部分学者研究利用偏离特征值对应特征向量分析比较不同行业的股票相关性结构特征（Han 等，2017；Kumar 和Deo，2012；Jiang 等，2014）。此外，偏相关系数分析还可以剔除部分中介效应，更深层次地揭示股票的相关性特性。Kenett 等（2010）、Kenett 等（2015）、Han 等（2017）[和杨红伟等（2018）通过比较原始相关矩阵和剔除市场指数因素的偏相关矩阵来分析相关性结构的变化情况。

本文的贡献在于：第一，利用随机矩阵理论，研究分析经贸摩擦爆发前后中国制造业股票相关性结构的变化，揭示制造业股票在不同时期的相关性结构差异，反映经贸摩擦对制造业股票系统性风险的影响；第二，基于偏相关系数理论，更深层次分析剔除市场指数因素后，制造业股票相关性结构中的市场效应。

二、基于随机矩阵理论的股票相关性分析原理

随机矩阵理论通过对比研究对象和随机系统在特征值和特征向量上的统计特性，能够区分“噪声”和真实信息。股票市场环境是非平稳的，难以确定两只股票价格变化相关性是随机的还是真正来源于两家公司之间的相互作用。利用随机矩阵理论，将真实收益相关矩阵和随机相关矩阵进行统计性质比较，能够有效解决这个问题。

另一方面，基于收益序列构建的Pearson相关系数能够提供有效信息，但是要提取这些信息存在困难。偏相关是一种统计度量，通过消除一些中介效应计算的偏相关系数，能够表明剔除的中介效应如何影响两个变量之间的相关性（Baba 等，2004）。基于偏相关系数的功能，将偏相关分析应用到股票收益时间序列中，可以剔除任意两只股票收益时间序列之间的共同影响因子，分析共同影响因子分别对这两只股票的影响。偏相关矩阵应用于股票相关性结构分析，能够更进一步研究相关性结构特征及其所含信息。本节主要介绍基于随机矩阵理论的股票相关性分析原理。

（一）随机矩阵理论简介

如果有N 个长度为T 的收益率序列，随机相关矩阵记为R，那么：

其中，A=（a）表示N×T 的随机矩阵，元素a都是随机的，且服从均值为0、标准差为1 的正态分布。

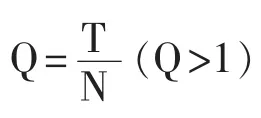
λ ∈［λ，λ］，λ和λ分别为RMT预测的最大特征值和最小特征值，且

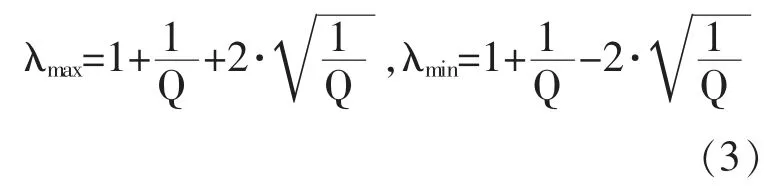
Laloux 等（1999）研究指出，若随机相关矩阵R 的特征值不含任何信息，则对应的特征向量分量的概率密度函数P（u）服从标准正态分布，见式（4）：

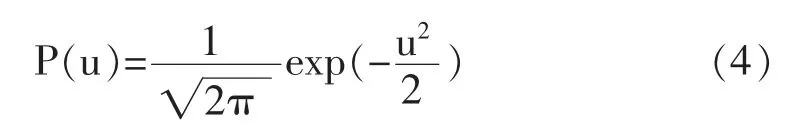
（二）真实收益相关矩阵

在股票相关性结构研究中，一般选取股票收益率构建真实收益相关矩阵。利用式（5）计算股票价格对数收益率r（t）：

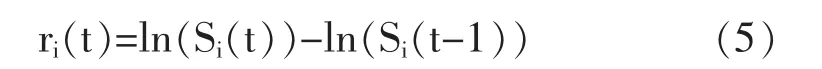
其中，r（t）表示第i 只股票第t 日的价格对数收益率，i=1，2，…，N，t=1，2，…，T，N 表示股票总数，T 为时间长度，S（t）表示第i 只股票第t 日的当日收盘价。

由于不同股票的价格波动程度不同，需要对股票价格对数收益率进行标准化处理，见式（6）：

采用Pearson 相关系数公式计算不同股票之间的相关系数，并构造相关矩阵。利用式（7）计算股票和股票之间的相关系数。

真实收益相关矩阵C=（C），C代表股票i 和股票j 之间的相关系数。由相关系数的定义可知，C的取值范围是［-1，1］。C∈（0，1］表示股票i 和股票j 正相关，即两只股票的价格同涨同跌；C∈［-1，0）表示股票i和股票j 负相关，即两只股票的价格变动方向相反；C=0 表示股票i 和股票j 不相关，即股票i 的价格和股票j 的价格互不影响。

（三）真实收益偏相关矩阵

根据Han 等（2017）的研究，对于任意的股票收益率时间序列，可以剔除共有的市场因素，采用单因子模型提取特质分量：

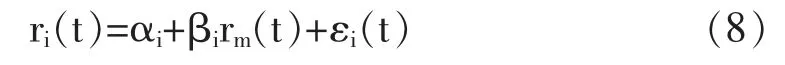
式中，r（t）为市场指数对数收益率时间序列，ε（t）为残差，代表股票i 自身的特性。通过残差间的相关系数p定义股票i 和股票j 相对于市场指数的真实收益偏相关系数，见式（9）：

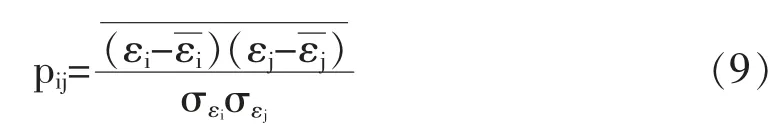
其中，σ和σ分别为ε（t）、ε（t）的标准差。对于单只股票而言，单因子模型中的市场指数代表所有股票的共同影响因子，反映的是股票的系统风险，即对全体股票收益产生影响的全局性因素。本文计算过程采用简化计算公式（Kenett 等，2010），偏相关矩阵P 的元素为P：

其中，C和C分别为r、r和r的相关系数。

根据上述公式，可以计算股票对数价格的真实收益相关矩阵，以及剔除市场指数效应后的真实收益偏相关矩阵。基于RMT 理论，将两种性质的矩阵进行相关系数、特征值和特征向量的比较，可以很好地分析经贸摩擦爆发前后制造业股票相关性结构特征的变化以及股票间相关性结构含有的市场信息，从而分析经贸摩擦对制造业股票系统性风险的影响。

三、制造业股票相关性结构特征演变的实证分析

（一）数据描述

本文选取中国证监会行业分类中的计算机、通信及电子设备制造业的230 只A 股股票和沪深300 指数的日收盘价作为原始数据，其中上海证券交易所A 股58 只，深圳证券交易所A 股172 只，样本时间跨度为2016 年1 月1 日至2020 年12 月31 日，共1218 个交易日。考虑数据的有效性，本文剔除了连续停盘超过100 个交易日的29 只股票，其中上海证券交易所8 只，深圳证券交易所21 只，仅对剩余的201 只股票进行实证分析，数据来源于wind 数据库。样本选取理由如下：一是样本时间跨度正好包含所要研究对比的2016-2017 年和2018-2020 年两个时间区间。二是美国“301 调查”涉及各项关税加征，征税内容大多集中在中国知识产权领域（如高端制造业），选择计算机、通信和电子设备制造业能够较好地代表中国知识产权类产品，对这一行业进行研究能够了解中美经贸摩擦对制造业股市的直接影响。三是选择沪深300 指数作为A 股市场代表，能够反映沪深两个市场的整体走势，与本文研究的样本相契合。

（二）相关矩阵和偏相关矩阵的比较分析

1.相关系数和偏相关系数的统计特性比较分析。根据式（5）、式（6）、式（7）和式（10），通过分析2016-2017 年间（即经贸摩擦爆发之前）和2018-2020 年间（即经贸摩擦爆发之后）两个时间段内A 股中201 只计算机、通信及电子设备制造业股票价格对数收益率的相关矩阵C、C和偏相关矩阵P、P，得到相关系数C的概率密度分布{f（C），i≠j}、偏相关系数P的概率密度分布{f（P），i≠j}以及相关系数和偏相关系数的描述性统计，结果见图1 和表1。

图1 和表1 表明：（1）制造业股票真实收益相关系数分布和偏相关系数分布都偏离标准正态分布。2016-2017 年间和2018-2020 年间均以正均值为中心，这表明中国制造业股票市场上，股票价格波动的相关性中，正相关比负相关更为普遍。2018-2020 年间的相关系数矩阵中，最小值为0.06，说明经贸摩擦爆发后，制造业股票间价格变动更为趋同，股价同涨同跌。经贸摩擦的爆发加剧了制造业股票系统性风险。

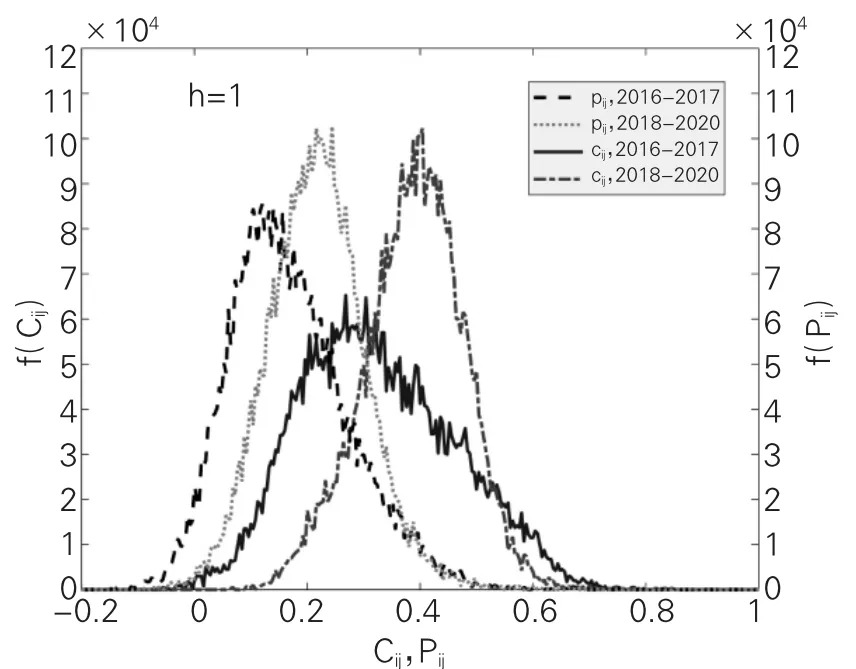
图1 真实收益相关系数Cij 和偏相关系数Pij 概率密度分布

表1 真实收益相关系数和偏相关系数描述性统计（下三角元素）

（2）经贸摩擦爆发前后制造业股票的真实收益相关系数概率密度分布存在较大的差异。2016-2017 年间相关系数均值为0.32，小于2018-2020 年间的均值0.39，这进一步表明经贸摩擦爆发之后，中国制造业股票市场的系统性风险上升。两个时间段内的真实收益相关系数分布的标准差存在差异，意味着中国制造业股票间的相关性具有时变性。特别是经贸摩擦爆发后股票间的相关性高于经贸摩擦爆发之前。

（3）经贸摩擦爆发前后的真实收益偏相关系数概率密度分布差异与相关系数分布差异相比没有缩小。剔除沪深300 指数后，2016-2017 年和2018-2020 年的偏相关系数分布都发生了较大变化，平均偏相关系数（分别为0.17 和0.22）显著变小，比相关系数均值更接近于0。然而，经贸摩擦爆发前后的偏相关系数分布没有出现缩小的现象。我们对2016-2017 年和2018-2020 年的平均偏相关系数进行T 均值检验。结果显示，在显著水平5%下，经贸摩擦爆发前后偏相关系数均值显著不相等。这表明沪深300 指数不能完全代表对制造业股市产生共同影响的市场效应，可能的原因是选择的样本是制造业并非全行业，即针对中国制造业增加关税的经贸摩擦对中国制造业行业造成严重的冲击，增强了整个行业内股票间的联动性，加剧了制造业股票的系统性风险，这与潘攀（2015）的研究结论相一致。该实证研究表明，各行业之间的股票相关性高于全行业的股票相关性（潘攀，2015）。所以，在剔除市场指数后，对制造业股票有着一致影响的共同因子很有可能来自行业效应。

2.特征值分布比较分析。2016-2017 年间N=201、T=488，2018-2020 年间N=201、T=729，根据式（3）计算得出2016-2017年的RMT预测特征值范围为[0.1283，2.6955]，2018-2019 年的RMT 预测特征值范围为[0.2255，2.3259]。真实收益相关矩阵和偏相关矩阵的特征值同RMT 预测特征值的比较见表2 和图2。

最大特征值可以反映市场效应（Plerou等，2002；Kulkarni 和Deo，2007；Namaki 等，2011；Wilcox 和 Gebbie，2004；Wilcox 和Gebbie，2007），同时可以同平均相关系数一样起到衡量系统风险的作用（Han等，2017；Billio 等，2012）。从表2 和图2可以看到：（1）经贸摩擦的爆发提高了相关矩阵最大特征值和偏相关矩阵最大特征值。C的最大特征值为80.2370，大于C2的最大特征值70.9499，剔除沪深300 指数，P的最大特征值为46.5778，大于P的最大特征值39.6369。

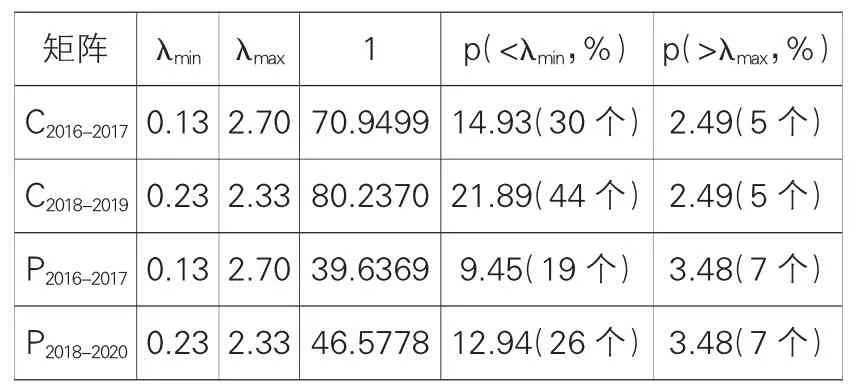
表2 真实收益相关矩阵和偏相关矩阵特征值同RMT 预测特征值的比较

（2）经贸摩擦的爆发增大了真实收益相关矩阵和偏相关矩阵的偏离特征值比例。C2超出RMT 预测范围的特征值有35 个，占比17.42%；P超出RMT 预测范围特征值的比例为12.94%；C有49 个特征值超出预测范围，占24.38%；C超过预测范围的特征值比例为16.62%，共有33 个。结果表明，经贸摩擦的爆发提高了中国制造业股市的系统性风险。

图2 分别显示了真实收益相关矩阵和偏相关矩阵的特征值与RMT 预测特征值的概率密度分布情况。可以看到，偏相关矩阵特征值概率密度分布更加接近RMT 预测特征值的分布，原始相关矩阵特征值的分布明显偏离RMT 的预测。

图2 真实收益相关矩阵和偏相关矩阵特征值与RMT 预测的特征值概率密度分布比较

3.特征向量分布的动态分析。特征向量分量分布表示样本股票对特征向量的贡献，偏离特征值的特征向量分量的符号含有一定的经济信息（Han 等，2017；杨红伟等，2018；Jiang 等，2012）。因此，特征向量分量分布的变动情况可以反映股票相关性结构的动态演变。图3 展示的是2016-2017年和2018-2020 年两个时间段内真实收益相关矩阵和偏相关矩阵前五大特征值对应的特征向量分量分布。前五大特征值对应的特征向量分量分别记为u、u、u、u和u。可以明显看到，P和P的u对应分量符号方向相反，说明经贸摩擦的爆发使得制造业股票相关性结构发生明显变化。

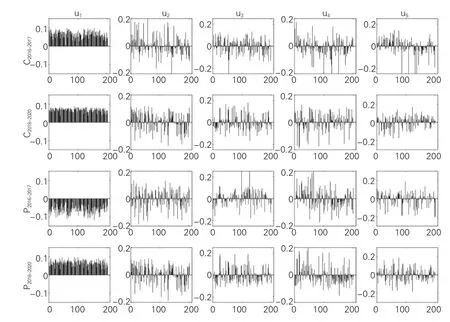
图3 不同阶段C 和P 的前五大特征值对应特征向量的分量分布

图4展示的是C、P、C和P的u-u相关关系热力图，清晰地显示了前五大特征向量分量分布的变化情况，揭示了中美经贸摩擦对股票市场相关性结构的动态影响。第一行的两个图分别展示 了C和P（左图）、C和P（右图）的前五大特征值对应特征向量的相关关系。由图4 可知，C和P的u、u之间呈现显著的负相关关系，u之间的相关系数为-0.90，表明剔除市场指数效应后，201 只股票之间的相关性发生了较大变动，进一步证实市场指数对股票相关性结构的影响；C和P的u-u之间的相关性显著为正，说明剔除市场指数后股票间的关联性依旧稳健，这是因为经贸摩擦爆发后，剔除市场指数虽然能够减弱股票间关联性，但是经贸摩擦增强了制造业股票间的关联性，加剧了对所有制造业股票有共同影响的行业效应。

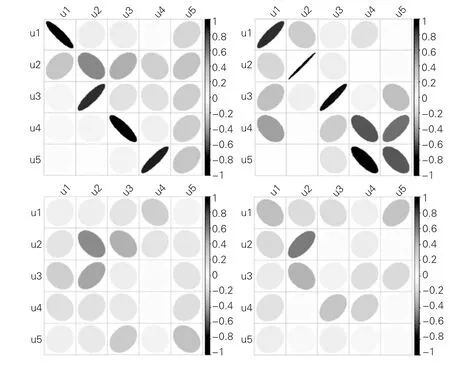
图4 相关矩阵和偏相关矩阵前五大特征向量的相关性热力图

第二行的结果展示了不同时间段的相关矩阵或偏相关矩阵的前五大特征值对应特征向量之间的相关关系图。C和C的u是正相关的，u-u则是负相关关系或者无明显的相关关系；P和P的u间存在负相关关系。结果表明，无论是否剔除市场效应，201 只制造业的股票相关性结构在中美经贸摩擦爆发前后都有着显著变化。再次揭示了经贸摩擦给制造业带来的行业冲击，使得股票间相关性增强。

（三）偏相关矩阵的市场效应分析

市场效应是指对所有股票有着共同影响的市场特征。市场效应的特征是最大特征值对应特征向量定义的投资组合收益序列和市场指数收益序列间存在良好的线性关系（Plerou 等，2002）。相关文献研究指出（Plerou 等，2002；Han 等，2017；Kumar 和Deo，2012；Patrick 等，2019），偏 离RMT 预测特征值范围的真实收益相关矩阵能够反映不同股票群体的集体行为，大的偏离特征值反映出行业特性，最大特征值通常反映市场效应，即式（8）中的共同因子——市场指数。据此，预测剔除市场指数的影响后，偏相关矩阵的最大特征值与市场不再相关。然而，前文的分析中得出，剔除沪深300指数得到的偏相关矩阵的最大特征值依旧含有对201 只股票有着共同影响的市场信息。本节通过比较经贸摩擦爆发前后偏相关矩阵最大特征值对应特征向量定义的投资组合与沪深300 指数的对数收益序列，分析偏相关矩阵的最大特征值的信息含量，进一步揭示经贸摩擦爆发对制造业整个行业的系统性影响。

投资组合的收益率时间序列根据如下步骤确定（Han 等，2017）：

（1）确定组合权重w，w 定义为最大特征值对应特征向量的每个元素在201 个元素中的比重，投资第i 只股票的权重w的计算公式为：

（2）确定投资组合的组合收益序列R（t），由组合中201 只股票的收益率r（t）和各自的投资比重w决定：

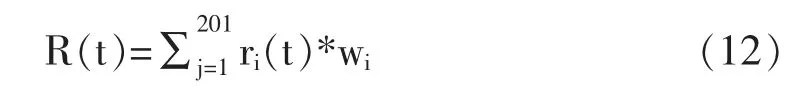
（3）计算沪深300 指数收益率时间序列R（t）：

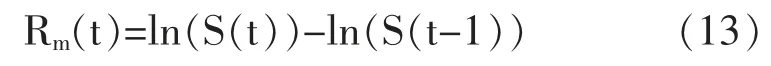
其中，S（t）为第t 日沪深300 指数的收盘价。

利用式（11）、式（12）和式（13），计算分别由2016-2017 年和2018-2020 年偏相关矩阵P 的最大特征值对应特征向量定义的投资组合收益序列R′，次大特征值对应特征向量定义的投资组合收益序列R′，以及沪深300 指数收益序列R，对应的收益时间序列见图5。可以看到，经贸摩擦爆发前后，R′和R呈现明显的一致性，而R′和R没有显著的相似性。进一步地，图6 展示了经贸摩擦爆发前后真实收益相关矩阵与偏相关矩阵的最大特征值对应特征向量定义的投资组合收益序列R和R′分别与R的回归拟合图。结合表3 可以明确，在0.01显著性水平下，经贸摩擦爆发前后，R和R′分别与R有显著的线性正相关关系。结果表明，剔除沪深300 指数，偏相关矩阵中还存在制造业股票的共同影响因素，该信息存储在偏相关矩阵的最大特征值及其相应的特征向量中。

图6 最大特征值对应特征向量定义的投资组合收益与市场指数关系

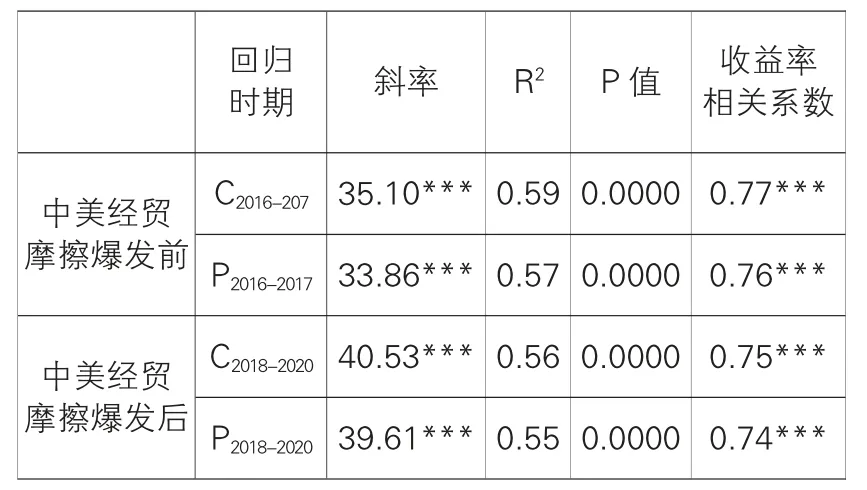
表3 最大特征值对应特征向量定义的投资组合与沪深300 指数收益序列回归结果及相关性

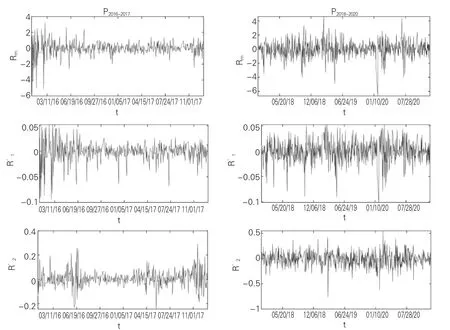
图5 偏相关矩阵的u1 和u2 定义的投资组合收益序列和沪深300 指数收益序列

经贸摩擦爆发后，相关矩阵最大特征值对应特征向量定义的投资组合收益率与沪深300 指数的收益率之间的相关系数为0.75，偏相关矩阵对应值为0.74，两者变化不大，说明经贸摩擦不仅强化了整个股票市场间的关联，还增强了制造业股票间的相关性，表现为偏相关矩阵最大特征值中含有的信息对制造业股票的共同影响依旧显著。

前文提到，C 和P 的最大特征值代表市场效应，对应的特征向量分量分布集中；波动时期市场效应会增强，最大特征值会增大。据此，我们推测，波动时期最大特征值对应特征向量分量的分布比稳定期集中。我们通过比较C、C、P和P的最大特征值对应的特征向量分布进行验证。从图7 可以看到，C的最大特征值对应特征向量概率密度比C更加高而窄，C和C的最大特征值对应特征向量的分布均比P和P的分布集中。综上所述，可以验证相对不稳定时期相关矩阵的最大特征值对应特征向量的分布更加集中，系统性风险更高。同时证明了剔除市场指数效应后，偏相关矩阵最大特征值代表的市场效应减弱。

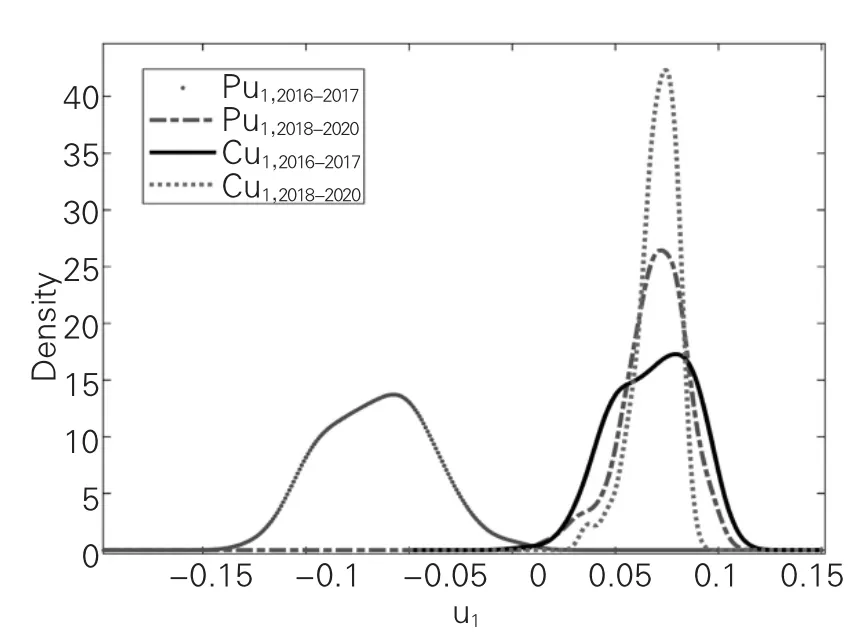
图7 最大特征值对应特征向量的概率密度分布图

四、相关结论与讨论

本文基于随机矩阵理论，运用偏相关分析方法，以2016-2020 年中国证监会行业分类中的计算机、通信及电子设备制造业A 股股票日收盘价为原始数据，对2016-2017 年和2018-2020 年的制造业股票相关矩阵和偏相关矩阵的平均相关系数、最大特征值和特征向量的信息进行了比较，探讨中美经贸摩擦爆发前后制造业股票相关性结构的变动，进一步揭示经贸摩擦对制造业股票系统性风险的影响。研究表明：

第一，经贸摩擦对中国制造业股票的相关性结构有显著的动态影响，经贸摩擦增强了制造业股票间的相关性，加剧了制造业股票的系统风险。经贸摩擦爆发前后，相关系数分布和偏相关系数分布都存在差异，表明中国制造业股票相关性结构具有时变性。经贸摩擦爆发后，相关系数全为正数，偏相关矩阵最大特征值对应特征向量分量符号由负变为正，相关系数均值、相关矩阵最大特征值以及偏离RMT 预测范围的相关矩阵特征值比例均有所提高，表明中美经贸摩擦爆发之后制造业股票间的相关性更为密切，股票价格波动方向一致，加剧了制造业股票的系统风险和市场的系统风险。

第二，沪深300 指数是制造业股票相关性结构的重要影响因素，可部分代表对制造业股票产生共同影响的市场效应，剩余的市场效应来自制造业的行业效应。因为本文所选样本来源于同一个行业而非全行业，经贸摩擦不仅加据了市场的系统风险，还增强了制造业股票间的关联性，制造业股票价格同涨同跌，扩大制造业股市系统风险。经贸摩擦爆发前后，剔除沪深300 指数的偏相关系数均值和最大特征值与相关矩阵相比有明显的降低，表明市场指数能够影响制造业股票间的相关性；然而，两个阶段偏相关系数分布存在差异，经贸摩擦增大了偏相关系数平均值和偏相关矩阵最大特征值，揭示了经贸摩擦对制造业上市股票相关性结构的显著影响。通过对偏相关矩阵进行市场效应分析可知，R′与R有显著的线性正相关关系，揭示了剔除沪深300 指数的影响之后，仅消除了部分市场效应的影响，偏相关矩阵中依旧含有对所有股票有着相同作用的因素，这类因素可能包含行业信息。

第三，对比不同阶段的真实收益相关矩阵和偏相关矩阵，发现市场波动时期最大特征值对应特征向量分布更集中。这是因为市场的波动增大了最大特征值，加大了市场对股市的共同作用力。从前五大特征值对应特征向量的分析来看，中美经贸摩擦的爆发的确改变了股票间的相关性结构。

基于上述研究结论，本文建议：一是市场监管者可以考虑将股票间的相关性结构的演化纳入市场风险管理中，当股票间的联动增强时，表明市场系统风险提高，监管者可以设置股票相关性结构预警线，将风险控制在一定范围之内；二是投资者进行投资决策时，应当考虑不同股票间相关性结构的变动，不能忽略市场整体环境的影响，同时不能仅仅根据市场环境的变动而忽略公司本身的价值，完全受市场主导决策，要综合多方因素考虑，进行投资风险管理；三是上市公司价值反映在股票价格当中，经贸摩擦背景下中国制造业股价的下跌表明股民对制造业公司发展前景担忧，制造业企业必须加大自身研发力度，加快技术创新步伐，提高效率，降低成本，增强企业竞争力，从而增强股民对企业发展的信心，有效缓解经贸摩擦带来的负面影响。