基于深度学习的工业机器人摩擦力补偿方法研究
汪朋朋 殷兴国 寇斌














文章编号:1007-2373(2022)01-0027-08
摘要 非线性摩擦力极大影响了机器人的运动性能,摩擦力补偿问题是机器人运动控制中的共性问题。传统的线性和非线性摩擦力补偿模型在实际应用中效果并不理想,而神经网络模型具有固有的非线性特性,对于处理非线性摩擦力具有较大的优势。文章基于深度学习算法,将动力学模型中的非线性环节作为广义的摩擦力处理,根据转矩、速度、位置等相关量学习出系统的摩擦力模型,然后在规划力矩中加入一个大小相同、方向相反的力将摩擦力抵消,从而实现机器人关节摩擦力的补偿。通过构建摩擦力补偿实验平台,测试了机器人在不同路径下的力矩相对误差。研究结果表明基于深度学习的摩擦力补偿模型对于提高力矩精度具有重要作用。
关 键 词 非线性摩擦;摩擦力补偿;深度学习;注意力机制
中图分类号 TP242 文献标志码 A
Research on friction compensation of industrial robot
based on deep learning
WANG Pengpeng1,2, YIN Xingguo1, KOU Bin2
(1. Shanghai Gene Automation Technology Ltd, Shanghai 201112, China; 2. Academy for Engineering and Technology, Fudan University, Shanghai 200433, China)
Abstract Non-linear friction greatly affects the robot's motion performance, and friction compensation is a common problem in robot motion control. Traditional linear and non-linear friction compensation models are not ideal in practical applications. However, neural network models have inherent non-linear characteristics and have greater advantages in processing non-linear friction. Based on the deep learning algorithm, the article treats the nonlinear part in the dynamic model as a generalized friction force, learns the friction force model of the system according to related quantities such as torque, speed, and position, and then a force of the same magnitude and opposite direction is added to the planning torque to offset the friction force, so as to realize the compensation of the friction of the robot joints. By constructing an experimental platform for friction compensation, the relative error of the torque of the robot under different paths was tested. The research results show that the friction compensation model based on deep learning plays an important role in improving the torque accuracy.
Key words non-linear friction; friction compensation; deep learning; attention mechanism
0 引言
机器人在工业生产、服务、医疗等领域的应用不断增加,对机器人的运动性能提出了更高的要求。在机器人运动控制中,摩擦、温度、磨损、空气阻力等非线性环节是动力学模型误差的主要来源,这些非线性环节极大影响了机器人的运动性能。其中,机器人的关节摩擦是其动力学模型误差的最主要来源,非线性摩擦是影响机器人低速运动性能的主要因素之一。摩擦力的影响使得机器人存在难以消除的稳态误差,从而使定位精度降低;在低速运动时产生爬行现象;在往复运动中产生不连续运动,从而引起振动;在高速运动时产生较大的跟随误差。摩擦补偿问题成为机器人运动控制中的共性问题。
摩擦力的建模常使用簡单的多段线性模型,但该方法准确度不高,不适用于需要精准力控、高速和高精度的场合。Canudas[1]提出了LuGre非线性模型,其能较好的描述预滑动位移、变静摩擦力、Hess滞后效应[2]、爬行、Stribeck效应[3]等动静态摩擦特性,但实际应用中,存在建模困难,摩擦力在静止和低速的时候难以精确测量,难以确定模型中的参数等问题,因此无法达到预想的控制效果。近年来,模糊控制[4]、自适应控制[5]、神经网络[6]等智能算法被引入到摩擦补偿之中,由于智能算法处理非线性的能力比较强,在摩擦补偿中有着广阔的应用前景。
文章基于深度学习算法,将动力学模型中的非线性环节作为广义的摩擦力处理,根据转矩、速度、位置等相关量学习出系统的摩擦力,在前馈控制力矩中加入一个大小相同、方向相反的力将摩擦力抵消,从而实现机器人关节摩擦力矩的补偿。
1 摩擦模型
1.1 机械臂的摩擦力
机械臂运动过程中,存在静摩擦、库仑摩擦、粘性摩擦等摩擦力,且具有非线性特性。通常,接触面由相对静止到相对运动的过程中,按决定摩擦力大小的不同主要因素,可以分为4个阶段[1]:1)弹性形变阶段;2)边界润滑阶段;3)部分液体润滑阶段;4)全液体润滑阶段。认为在第1阶段,摩擦力与速度无关,在第2阶段表现为摩擦力(库仑摩擦)小于静摩擦力[Fs],第3阶段滑动摩擦与速度并不是简单的线性关系,第4阶段则会引入粘滞摩擦系数。
考虑到摩擦力的静态特性与动态特性,无论是使用经典的数学模型还是使用神经网络模型,在构建完整的摩擦力补偿方案时,需要考虑如下3种具体场景:
1)微观启动/停止阶段:摩擦力补偿算法应重点关注“启动/停止”临界阶段的表现,即需要更多地考虑针对微观静摩擦的启动/停止阶段进行建模和数据采集,针对图1中的前两个阶段。
2)宏观加/减速阶段:机械臂有实际宏观的加减速运动。此时考虑到摩擦力动态效应中的滞后效应(当物体作单向变速运动时,摩擦力的变化会滞后于速度变化大约几到几十毫秒),說明摩擦既是即时速度和负载的函数,又是历史速度和负载的函数。
3)宏观匀速运动阶段:聚焦于摩擦力补偿算法在宏观匀速运动阶段的表现,此时数据采集相对简单,但仍然需要考虑由于机械臂位姿变化导致的轴向荷载变化对摩擦力大小的影响。
1.2 机器人动力学中的摩擦力模型
基于关节空间的机器人动力学模型可以描述如下,将摩擦力显式表达出来:
式中:[q∈Rn]是机器人在关节空间中的位置(n表示机器人第n个关节);[q]为机器人关节速度;[q]为机器人关节加速度;[M(q)]为机器人惯量矩阵;[Cq,qq]表示机器人科氏力与离心力;[G(q)]为机器人重力;[Fq]表示机器人摩擦力;[τ]表示各关节的驱动力矩。
理论上,不使用机器人动力学建模,仅利用深度学习进行摩擦力建模,也可以学习出相应的摩擦力补偿模型。但这种简单的建模方式,摩擦力与其他各项力矩(惯性力矩、科氏力与离心力、重力)之间存在非线性耦合,不利于实际的力矩解耦控制。因此应尽可能精确求解出动力学模型中的惯性力矩、科氏力与离心力、重力,从而得到经过解耦的摩擦力补偿模型。
2 摩擦补偿方案设计
2.1 整体方案设计
机械臂运动过程中,多种摩擦力作用于实际系统,给机器人带来诸多不利影响。为了降低甚至消除摩擦力对机器人系统的影响,一种可行的方案是:在控制器给实际系统发送控制命令时,同时在控制命令中加入一个抵消摩擦力的力矩,即摩擦力补偿力矩,如图2所示。研究试图得到其中的摩擦模型,考虑到摩擦力的影响因素较为复杂,存在静摩擦、滑动摩擦、粘性摩擦等摩擦力,且存在非线性特性,研究采用深度学习神经网络模型,得到摩擦模型以后,在前馈控制力矩中加入一个大小相同、方向相反的力将摩擦力抵消,从而实现机器人关节摩擦力矩的补偿。
通过采集机械臂运行中的位移、速度、力矩等数据,利用动力学模型计算理论力矩,并采集伺服系统反馈的实际转矩,得到理论力矩和实测力矩的误差,即摩擦损失力矩。求出各个模型对该损失力矩的参数梯度,并利用优化算法优化模型中的参数,最终得到摩擦力补偿模型。
通过上述方案,得到某一型号机械臂的通用摩擦补偿模型以后,可以将模型迁移到该型号新出厂机械臂上。但由于同一型号的不同机器臂生产制造差异、实际工况不同,各机器臂的摩擦力也存在一些差异。可以通过对每台机械臂执行单独的微调学习过程,从而得到针对具体一台机械臂最优的摩擦力补偿模型。
另外,随着机械臂的使用和工况变化,机械臂有可能产生磨损,润滑效果变差等情况,原有的摩擦补偿参数可能不适用,因此需要构建一个能够针对当前工况的即时模型,即能够自动采集数据,自动训练、自动部署的摩擦力补偿模型在线平台。
2.2 数据
2.2.1 数据采集
根据上述方案,摩擦力补偿模型的主要输入数据量为理论力矩与实际力矩的误差。因此在数据采集过程中,应重点考虑引起系统转矩误差的影响因素,根据这些影响因素,确定数据采集方案。引起系统转矩误差的主要因素有:
1)各轴电机运动的瞬时(角)速度ω不同,引起的转矩误差随瞬时速度大小的变化;
2)各轴转动过程中由于转轴不同位置q的物理特性、齿轮间隙等不完全一致,引起的转矩误差随位移的变化;
3)各轴的电机减速器的温度T变化导致的微观接触面膨胀、收缩、润滑差异,引起的转矩误差随温度的变化;
4)动力学模型的计算理论力矩和实际力矩之间存在的力矩误差;
5)各轴测量转矩与实际转矩的力矩误差。
根据以上影响因素,确定数据采集的方案:1)采集不同速度下的转矩值;2)采集机器人在不同位置下的转矩值;3)采集不同温度下的转矩值;4)利用动力学参数辨识提高动力学参数的精度,减小动力学模型的力矩误差;5)利用传感器测量实际转矩,校准伺服系统的转矩精度等。
具体可以如下操作:编程指定机械臂的运动路径,让机器人每个轴单独以不同的位姿、不同速度进行运动,过程中每隔4~10 ms采样间隔记录机械臂的负载、位置、速度、转矩、温度等数据。
2.2.2 数据类型和数据量
数据采集共43列数据,其中,各轴数据包括机器人1至6轴的数据;各轴理论计算力矩为根据动力学模型计算的理论力矩,各轴实际力矩为通过伺服采集的力矩;如表1所示。
2.2.3 数据划分
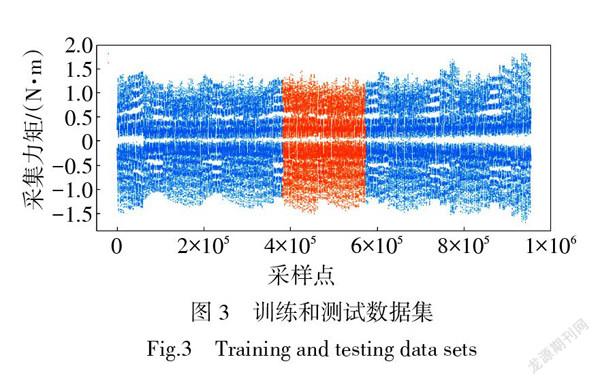
研究将采集到的数据集划分为训练集、测试集。按照不同运动路径,80%的数据用于训练,20%的数据用于测试,如图3所示。
2.2.4 数据处理
在模型训练之前,使用了必要的方法对采集数据进行处理,主要包括数据清洗,数据划分,数据均衡,数据增强等。1)数据采集时,由于机器人运动的路径数据可能存在重复采集、数据缺失等问题,利用数据清洗可以保證数据的完整性、唯一性、一致性等。2)针对机器人运动中存在的加减速、匀速运动的情况,以及存在的低速、高速运行的情况,采用数据划分方法,可以提前对数据进行分类,方便得到针对性的神经网络模型。3)数据采集时,由于不能遍历机器人所有工况下的运动数据,为了避免数据不平衡的问题,采用数据均衡可以使模型补偿效果更佳。4)为了提高模型的鲁棒性,对采集的数据利用正负变换、平移变换、加噪音等数据增强手段,从而提升摩擦力补偿模型的泛化能力。
2.3 模型
机器人关节摩擦力具有明显的非线性特性。神经网络模型是一种非线性的映射方式,具有固有的非线性特性。利用神经网络建立的摩擦力补偿模型,能将输入的特征量(转矩、速度、位置、温度等)映射到网络的输出结果(摩擦力),并可依照其误差大小的损失函数,来调整网络中的加权值使模型达到收敛。
研究中,通过构建深度学习网络模型,搭建如图4所示的前馈结构。所构建的神经网络模型包括若干个堆叠结构模块,模块数量可通过程序API更改。其中,每个堆叠结构模块包括批量标准化层、全连接层和激活层(Tanh Shrink),如图4所示。
神经网络的结构主要由输入层,隐藏层,输出层构成。输入层的神经元个数由输入量的特征数目来决定,针对摩擦补偿算法的模型,输入量为各轴位置、速度、理论力矩、实际力矩、温度这5项,因此输入层的神经元个数为5。输出层的神经元个数根据解决的问题来确定,即各轴的摩擦力,因此输出层的神经元个数为1。
隐藏层的层数及各层的神经元个数是可以调节的参数,而不同的层数和各层的神经元个数对模型的影响非常大。Jeff Heaton[7]指出,没有隐藏层时神经网络只能用于表示线性分离函数;隐藏层为1时可以拟合任何“包含从一个有限空间到另一个有限空间的连续映射”的函数;隐藏层为2时搭配适当的激活函数可以表示任意精度的任意决策边界,并且可以拟合任何精度的任何平滑映射;多个隐藏层可以学习复杂的描述。隐藏层的神经元太少将导致欠拟合(under fitting),相反,隐藏层中的神经元过多可能会导致过拟合(over fitting)。针对摩擦力补偿模型,由于机器人的摩擦力是非线性函数,并且与多种影响因素相关,因此隐藏层需要两层及以上,各隐藏层神经元个数不少于输入层的神经元个数且不宜过多。综合考虑模型的拟合能力和收敛难易程度,隐藏层的层数选择3层,各层的神经元个数选择5个,如图5所示。
研究基于PyTorch机器学习和深度学习库,网络模型参数可通过函数进行设置,构建模型的样例代码如图6所示。
值得注意的是,为解决模型在一些速度段补偿效果不佳的问题,在训练中引入注意力机制。如在电机换向、速度过零点时(此时的摩擦力比较复杂),存在补偿退化的现象,引入注意力机制,可以改善零速附近的补偿效果。注意力(Attention)机制[8]的定义如式(2):
式中:[Q(query)]、[K(key)]与[V(value)]3个矩阵均来自同一输入;注意力公式即计算[V]的加权表示;权重即[softmaxQKTdk],softmax操作是将结果归一化为概率分布,即和为1,softmax中的[QKTdk]为注意力的原始分数,通过计算[Q(query)]与[K(key)]的点积得到相似度分数,[dk]为一个query和key向量的维度,起到调节作用,使softmax不至于过大或过小(避免非0即1的情况)。
2.4 训练
研究中使用两种方式对数据进行划分,每种划分的数据会训练出两个不同的模型。这两种数据划分方式分别为:1)低速、高速情况(以100 rmp/min来区分高低速,根据经验选取);2)加减速、匀速情况。比较这两种数据划分方式,分析各模型的收敛情况,得到神经网络模型收敛过程如图7所示。
根据上述结果,可有如下结论:按照加减速/匀速进行数据划分的摩擦力补偿模型算法收敛最快,在迭代次数为20至30之间算法即收敛;匀速转态下的算法收敛速度最快,因为匀速状态下的摩擦力最为稳定,算法收敛最快符合常识;低速情况下算法收敛速度最慢,且经历多段收敛过程,这是由于低速情况下的摩擦力存在多种转态转换过程,可能涉及弹性形变阶段、边界润滑阶段、部分液体润滑多个阶段,需要对低速情况下的摩擦力模型更多关注。综合以上结论,本文后续实验均采用加减速/匀速方法进行数据划分。
3 摩擦补偿实验
3.1 实验平台
实验采用智昌川崎GRB007N型号机械臂,该型号机械臂负载7 kg,广泛用于焊接,上下料等场合,如图8a)所示,该机器人的标准DH参数定义如图8b)所示,其中,Z0为世界坐标系,Z1~Z6为1~6轴的轴线。
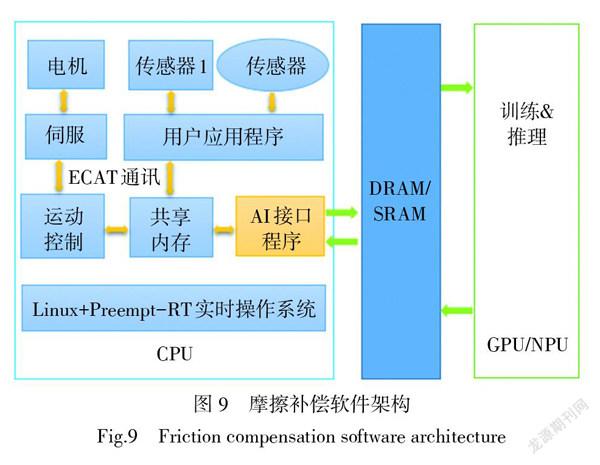
在自主开发的x86机器人运动控制器基础上,实验采用英伟达TX2 ARM嵌入式边缘计算平台,用于摩擦力补偿模型计算。针对ARM嵌入式智能计算平台,设计了如图9所示的软件架构。在CPU侧(机器人控制器)建立一块共享内存,将机器人运动控制的实时数据、外部传感数据等存入该内存,供AI接口程序调用、处理后,通过DRAM/SRAM加载到神经网络输入层。经模型训练或者推理运算后,输出的摩擦补偿力矩再经DRAM/SRAM传输到AI接口程序,最后送入共享内存区域,供运动控制程序和用户程序调用。
3.2 摩擦补偿实验
经算法补偿后,机器人的各轴力矩精度有较大提高。如图10所示:Axis1表示机器人的1轴(其轴线Z1,以此类推),各轴补偿前的规划力矩(蓝色曲线)与实际反馈力矩(黑色曲线)的误差较大,经摩擦补偿后的力矩(红色曲线)与实际反馈力矩(黑色曲线)之间的误差较小。
将训练好的模型,部署到实际系统中,即在前馈控制力矩中加入摩擦力补偿力矩,如图11为伺服系统采集的实际数据(以轴5数据为例):前两个周期的规划力矩中使用了摩擦補偿力矩(蓝色曲线所示),后两个周期未使用摩擦力补偿。可见,补偿后的力矩精度较补偿前有了很大提高。
针对机器人的不同工况,选取了机器人实际应用中的几种路径,比较无摩擦力补偿和有补偿后的力矩精度,定义相对误差如下式:
式中:[δ]为相对误差;[τref]为根据机器人动力学规划的理论力矩(不包括摩擦力矩);[τF]即根据深度学习模型计算得到的摩擦力补偿力矩;[τfdb]为通过伺服系统采集的实测力矩。
如表2所示,未进行摩擦力补偿时,[τF]即为0。平均相对误差指各轴在不同路径下的相对误差的平均值;经摩擦力补偿后,机器人各轴在不同路径下的相对误差[δ],较补偿前均有不同程度的减小,大幅提高了力矩精度。
4 总结
文章利用深度学习算法,将动力学模型中的非线性环节作为广义的摩擦力处理,根据机械臂运行中的转矩、速度、位置等相关量学习出系统的摩擦力模型,然后在前馈控制力矩中,加入摩擦力补偿力矩,从而实现机器人关节摩擦力的补偿。通过构建摩擦力补偿实验平台,测试了机器人在不同路径下的力矩相对误差,补偿后机器人不同路径下各轴的平均相对误差[δ]较补偿前减小了28%~61%。结果表明,基于深度学习的摩擦力补偿模型对于提高力矩精度具有重要作用。为后续机器人的力控应用奠定了基础,对于降低机器人的成本,提升机器人的运动性能具有重要意义。
参考文献:
[1] CANUDAS DE WIT C,OLSSON H,ASTROM K J,et al. A new model for control of systems with friction[J]. IEEE Transactions on Automatic Control,1995,40(3):419-425.
[2] HESS D P,SOOM A. Friction at a lubricated line contact operating at oscillating sliding velocities[J]. Journal of Tribology,1990,112(1):147-152.
[3] RABINOWICZ E. The nature of the static and kinetic coefficients of friction[J]. Journal of Applied Physics,1951,22(11):1373-1379.
[4] MOSTEFAI L,DENAI M,SEHOON O,et al. Optimal control design for robust fuzzy friction compensation in a robot joint[J]. IEEE Transactions on Industrial Electronics,2009,56(10):3832-3839.
[5] TAN K K,HUANG S,LEE T H. Adaptive friction compensation with a time-delay friction model[J]. Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2004,218(3):173-183.
[6] KIM H M,PARK S H,HAN S I. Precise friction control for the nonlinear friction system using the friction state observer and sliding mode control with recurrent fuzzy neural networks[J]. Mechatronics,2009,19(6):805-815.
[7] HEATON J. The number of hidden layers[EB/OL]. (2017-06-01)[2021-10-15]. http://www. heatonresearch. com/2017/06/01/hidden-layers. html.
[8] VASWANI A,SHAZEER N,PARMAR N,et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems,December 4-9,2017. Long Beach,California,USA. 2017,12:6000-6010.
收稿日期:2021-10-28
基金项目:上海市科学技术委员会科研计划项目(18DZ1112600,18DZ1112602)
第一作者:汪朋朋(1991—),男,博士研究生。通信作者:殷兴国(1974—),男,高级工程师,xingguo.yin@geneautomation.com。

