分数阶离散Lorenz系统的动力学行为

梁雪峰, 刘晓君

(1.天水师范学院 数学与统计学院,甘肃 天水 741001; 2.西安邮电大学 理学院,陕西 西安 710121)

分数阶微积分虽然具有和经典微积分几乎同样长的研究历史,但是由于发展初期缺少合适的几何解释和实际应用而致使其发展较慢.近几十年,研究人员逐渐意识到分数阶微积分在建模等方面具有比整数阶微积分更加准确和恰当的特性[1]，同时在非线性动力学领域,分数阶非线性系统的动力学研究已经成为非常重要和热门的研究方向[2-4].

在对离散系统动力学的研究工作中,被研究比较早的是一维Logistic映射.由于二维映射起着从一维到高维的衔接作用,因此对二维映射中混沌现象的研究有助于认识和预测更复杂的高维动力系统的性态.在分数阶非线性动力学领域,人们提出了很多连续系统,并详细地研究了它们的动力学行为[5-8].相比之下,分数阶离散系统具有更加简单的形式和更加丰富的动力学行为.

本文中,笔者所研究的系统为一个分数阶离散Lorenz映射系统,其形式较一般的二维离散系统复杂[9].首先研究了系统随不同参数变化的动力学行为,发现系统发生了周期倍分岔和Hopf分岔.然后为了进一步研究系统的动力学行为,基于数值模拟,得到了系统随参数和分数阶的阶数同时变化的三维分岔图.通过三维分岔图可以发现,该映射系统随着阶数的逐渐减小,动力学行为变得越来越简单,最后完全进入周期窗口;随着阶数逐渐增大,动力学行为变得越来越复杂,周期窗口和混沌运动反复叠加.

1 系统描述

经典的Lorenz混沌系统的离散形式为

(1)

其中x(n),y(n)为状态变量,γ,δ为系统参数.系统(1)的一阶差分形式为

(2)

利用类Caputo差分,得到系统(1)所对应的分数阶Lorenz映射系统

(3)

其中0⟨q≤1为分数阶的阶数.系统(3)的数值解为

(4)

下述讨论中，积分下限a设定为0.当系统参数选择γ=1.25,δ=0.75,分数阶的阶数q=0.99时,系统(3)处于混沌态,其混沌吸引子如图1所示.

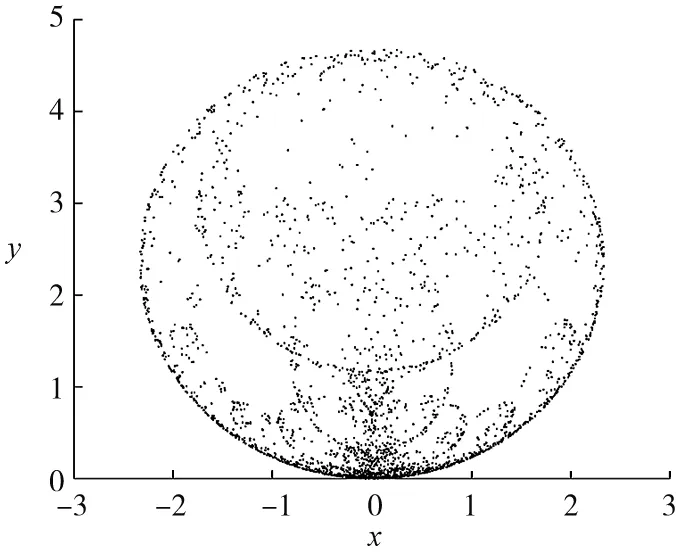
图1 系统(3)的混沌吸引子

2 动力学行为分析

通过数值模拟得到了系统(3)在不同参数值的动力学行为.当q=0.95时,系统在δ=0.46收敛到了不动点(图2a),当δ=0.47时系统有一个极限环吸引子(图2b).由此可见,系统随参数的变化发生了Hopf分岔.

图2 当q=0.95时,系统(3)关于不同δ的相图

为了从全局角度进一步研究系统(3),取属于不同吸引域的2个初值(x0,y0)=(0.1,0)和(x0,y0)=(-0.1,0),数值模拟得到系统(3)在2个初值条件下随δ变化的动力学行为,结果见图3.当δ=0.30时,系统收敛到了2个不动点(图3a);当δ=0.50时,系统收敛到了2个极限环(图3b);当δ从0.50增加到0.55时,极限环吸引子逐渐增大,并彼此靠近(图3c);当δ=0.56时,2个极限环破裂形成锁相(图3d);当δ从0.59增加到0.60时,2个极限环合并成一个混沌吸引子(图3e,f).

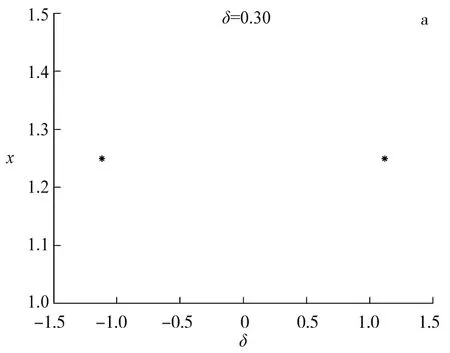
图3 系统(3)在2个初值(x0,y0)=(0.1,0)和(x0,y0)=(-0.1,0)的相图

取γ=1.25,δ=[0.2,1],q=[0.6,0.99],数值模拟得到了系统(3)随δ和q同时变化的分岔图,结果见图4.可以看到，系统具有丰富的动力学行为,发生了一系列的周期倍分岔和Hopf分岔.类似地,取δ=0.75,γ=[0.2,1.3],q=[0.7,0.99],图5给出了系统(3)随γ和q同时变化的分岔图.从2个分岔图可以看到,随着q的逐渐减小,离散分数阶Lorenz系统(3)的动力学行为变得越来越简单,最后完全处于周期运动状态;随着q的逐渐增大,离散分数阶Lorenz系统(3)的动力学行为变得越来越复杂,周期窗口和混沌窗口反复叠加.

图4 系统(3)随δ和q变化的三维分岔图

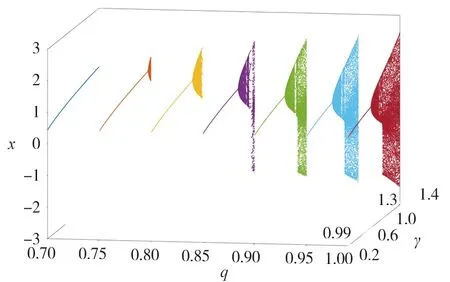
图5 系统(3)随γ和q变化的三维分岔图

3 结 论

所探讨的系统为一个分数阶离散Lorenz映射系统,其形式较一般的二维离散系统复杂.首先研究了系统随不同参数变化的动力学行为,发现系统发生了周期倍分岔和Hopf分岔.为了进一步研究系统的动力学行为,基于数值模拟,得到了系统随参数和分数阶的阶数同时变化的三维分岔图.通过三维分岔图可以发现,该映射系统随着阶数的逐渐减小,动力学行为变得越来越简单,最后完全进入周期窗口;随着阶数的逐渐增大,动力学行为变得越来越复杂,周期窗口和混沌运动反复叠加.