帝王蝶优化算法在铣削参数优化中的应用

张克道，陈向坚，王平心

（1.江苏科技大学 计算机学院，江苏 镇江 212100；2.江苏科技大学 理学院，江苏 镇江 212100）

0 引言

在进行切削加工时，选择合适的切削参数可以有效降低企业的生产成本，提高生产效率［1］。目前，企业通常根据加工经验或参考手册来进行参数的选择，这些参数往往较为保守，达不到最优值，虽然可以保证加工零件参数符合标准，但对于提高生产效率和降低生产成本帮助不大。

随着数学建模方法的不断完善和智能算法的发展，越来越多的学者通过数值优化选取合适的切削参数。文献［2］采用遗传算法进行切削参数优化，以加工时间和碳排放量为优化目标，但并未考虑加工成本，其优化后的切削参数虽然在加工时间和碳排放方面表现较好，但明显增加了加工成本；文献［3］运用混合多目标粒子群算法进行切削参数优化，将生产成本和生产效率两个目标通过协调系数转换为单目标问题，但转换系数通过经验确定，很大程度上影响了优化结果；文献［4］建立了以加工时间和能耗为目标的优化模型，采用粒子群算法寻优求解，实验验证了其有效性，但其模型所考虑的约束条件不够全面。文献［5］以加工时间为目标，采用多变异位遗传算法求解，仅考虑了零件表面粗糙度和机床有效功率两个约束条件，且没有考虑加工成本。

根据上述学者的研究结果及存在问题，本文从以下三方面改进。

（1）同时考虑生产效率和生产成本两个目标，避免出现高生产效率、高生产成本的情况。

（2）考虑实际加工时存在的各种约束条件，运用约束违反度方法处理约束，避免罚函数法中的罚因子取值问题影响优化结果。

（3）运用改进后的帝王蝶优化算法求解模型，将差分进化算法和粒子群算法中的一些思想加入其中，加快了寻优速度的同时有效避免陷入局部最优。

1 铣削参数优化

进行切削加工时，在保证加工零件参数符合标准的前提下，应追求更低的生产成本和更高的加工效率［6］。合理的切削参数的选择可以有效降低生产成本和提高生产效率，同时，正确的切削参数的选择也是加工零件质量的保障。但是由于切削参数的优化具有非常高的复杂性，工厂在实际加工时往往根据加工手册或以往的经验来进行切削参数的设置［7］，但是不管是根据加工手册还是以往的经验，这些切削参数往往较为保守，对降低生产成本和提高生产效率的帮助不大。因此，有必要对切削参数进行优化［8］。

1.1 铣削参数优化模型

进行铣削参数优化，首先要建立铣削参数优化的数学模型，主要包括变量的设计、约束条件和目标函数［9］。铣削参数有铣削速度v、进给量f和每次铣削深度ap。相比较于进给量和铣削速度，铣削深度对系统的影响较小，并且铣削深度可以由工件加工剩余量和实际加工时的具体要求来确定，所以此时可将铣削深度当作已知量进行后续的处理［10］。

1.1.1 模型目标函数

本文以最低生产成本和最大生产效率作为铣削参数优化目标。在进行铣削加工时，进行一次铣削加工的总加工时间Tw计算方式如下［10］：

其中，Tc为每道工序的换刀时间，Tot为辅助时间，通常情况下这两个时间为常量，与铣削参数优化关系不大。Tm为刀具的实际工作时间，刀具实际铣削时间可由下面公式求得：

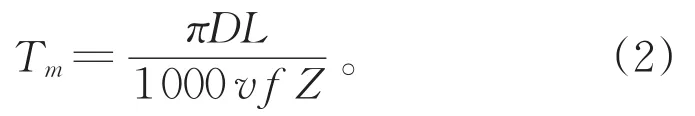
Th是一道工序的换刀时间，进行一道工序的换刀时间可由下面公式求得：

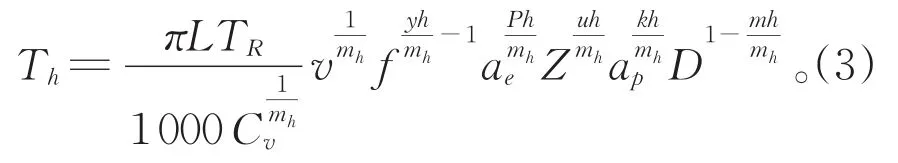
在上述这些公式中，D是刀具的直径；L是切削长度；v是切削速度；f是进行铣削加工时铣刀每齿的进给量；Z是铣刀的齿数；TR是换刀时间；ae是铣削的宽度；ap是切削的深度；Cv、kh、yh、mh、uh、Ph、qh都是刀具的耐磨度系数。

此时，最大生产效率函数为：

在进行铣削加工时，一道铣削加工的成本Cp计算方式如下：

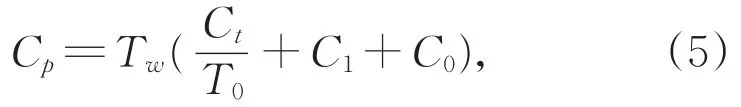
其中，Ct是刀具成本，T0是刀具的耐磨度，C1是单位时间里所需要的人工成本，C0是单位时间的管理成本。

那么最低生产成本函数可以表示如下：

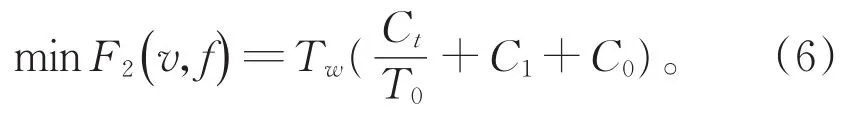
1.1.2 模型的约束条件

在进行生产加工时，由于加工材料、工件质量、工人安全和所用机床的主轴转速N、进给量f等因素的影响，需要对切削速度、进给量、切削力、机床功率和零件加工表面的粗糙度进行必要的约束［11］。

（1）切削速度约束如下：

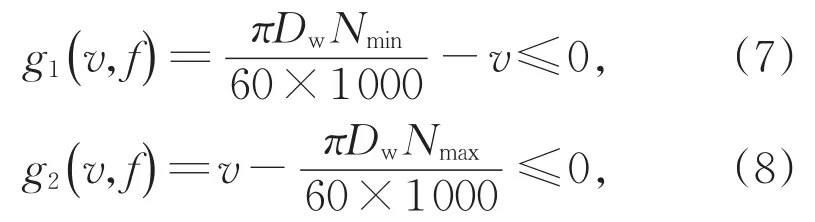
其中，Dw是加工零件的直径，Nmin是加工机床的最低主轴转速，Nmax是加工机床的最高主轴转速。

（2）进给量约束如下：

其中，vfmin是机床的最小切削进给速度，vmax是机床的最大切削进给速度。

（3）切削力约束：

其中，cF、xF、yF、uF、wF、qF、KFC是切削力参数，Ffmax是加工机床主轴最大进给力。

（4）加工机床功率约束：

其中，kp是比例系数，Pmax是最大有效切削功率，η是加工机床的转动系数。

（5）零件表面的粗糙度要求约束表达式如下：

其中，rε是刀尖的圆弧半径，Ramax是零件表面粗糙度的最大值。

经过上面的约束分析，切削加工参数的优化模型可以总结如下：

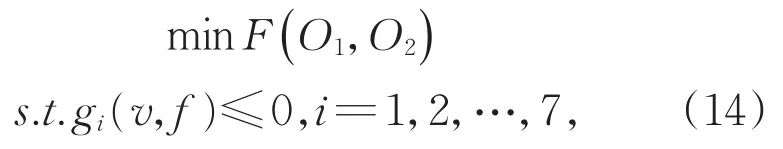
其中，O1是 F1(v，f)，O2是 F2(v，f)。

1.2 约束处理

从上面建立的铣削参数优化模型可以看出，铣削参数优化存在大量的非线性的约束条件。使用帝王蝶优化算法进行切削参数优化时，需要进行相应的约束处理。目前常见的约束处理办法是将约束优化问题转化为等价的无约束优化问题，目前使用较多的是罚函数法和约束违反度法进行无约束化处理。但由于罚函数法中罚因子的取值较为困难，影响优化效果，所以本文采用约束违反度法［12］。

约束违反函数G(X)的表达式如下：

其中，X是函数变量，gi(X)是第i个不等式约束，Pn是不等式约束的个数，hj(X)是第j个等式约束，qn是等式约束的个数，δ是形状系数，一般为一个值很小的实数，这里取δ=0.0001。约束违反函数G(X)的值越大，表示变量X的可行性越差，它的大小就是约束违反度。

2 优化算法

2.1 帝王蝶优化算法（monarch butterfly optimiza⁃tion，MBO）

2.1.1 帝王蝶迁移规则

在MBO算法中，所有蝴蝶被理想化，并遵循以下几个规则［13-14］：

（1）所有蝴蝶只在Land1、Land2活动，即这两个地区的蝴蝶就是整个蝴蝶种群。

（2）所有蝴蝶后代都由Land1或Land2中的蝴蝶经过迁移操作生成。

（3）为了保证蝴蝶种群的规模固定，规定如果产生的子代蝴蝶的适应度好于父代，则父代被子代所替换；若子代适应度低于父代，则子代直接被丢弃。

（4）适应度最好的蝴蝶将被保留并直接进入下一代，以此来保证种群的质量不会下降。

2.1.2MBO算法

进行MBO时，在初始化所有的参数后，首先要生成初始种群并计算初始种群的适应度值；按照适应度值对蝴蝶进行排序，然后根据规则更新蝴蝶的位置，直到满足终止条件。为了保证种群规模的稳定及尽可能减少适应度值的计算次数，对Land1和Land2位置的蝴蝶分别进行迁移操作和调整操作更新蝴蝶位置。

迁移操作：

迁移操作是指更新帝王蝶在Land1和Land2之间的位置。若将蝴蝶的总数设为NP，蝴蝶的迁移率为p，则Land1位置的蝴蝶数为ceil(p×NP)，Land2位置的蝴蝶数 为 NP-ceil(p×NP)，其中ceil(x)是指将x四舍五入取整数，为了方便表述，分别记Land1和Land2处的蝴蝶为Subset1和Subset2。则Subset1=ceil(p×NP)，Subset2=NP-ceil(p×NP)。

蝴蝶的迁移操作可表示为：

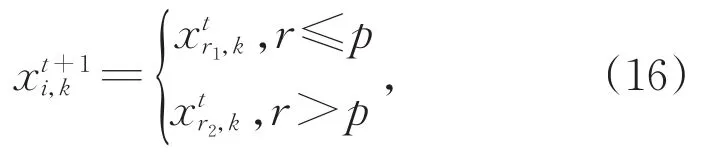
由公式（16）可知，迁移率p的大小决定了蝴蝶种群迁移操作的方向，若迁移率较大，则新生成的蝴蝶大多出现在Subset1中，若迁移率较小，则Subset2中有较多的子代蝴蝶。根据现实中蝴蝶有5个月在Land1，将p设置为5/12。

调整操作：

迁移操作是用子代蝴蝶来更新亲代，而调整操作是指更新蝴蝶个体的位置，而不需生成新的蝴蝶个体。

对于蝴蝶个体j，生成一个随机数rand，若rand≤p，则蝴蝶j按下面公式更新位置信息：

若rand>p，则蝴蝶j按下面公式更新位置信息：

2.2 快速非支配排序

对于任意解p，计算其两个属性：一是支配解p的解的数量np；二是解p支配的解的集合Sp。计算步骤如下：

Step1：令 i=0，支配解的数量 np=0，支配的解的集合Sp=∅。

Step2：对于集合P中的每个个体q，如果p≺q，将个体q添加到解p支配的解的集合Sp中；如果q≺p，支配解p的解的数量np=np+1。最后可以得到每个个体的支配数np和支配的解的集合Sp。将np=0的个体放到前端F1中，令p的非支配等级Prank=1。

Step3：令Q=∅，对于Fi中的每个个体p，进行以下操作：对于Sp中的个体q，nq=nq-1，若此时nq=0，则q的非支配等级qrank=i+1，然后将个体q添加到集合Q中。

Step4：若 Q≠∅，i=i+1，Fi=Q，转Step3；若Q=∅，停止。

2.3 多目标MBO算法

2.3.1 算法步骤

本文是将MBO算法应用于铣削参数优化，在铣削参数优化问题中会涉及多个优化目标，修改后的求解步骤如下［13-14］：

第一步，初始化参数。令t=0，随机生成父代种群P0，计算种群P0中各个解的目标函数值，将值赋给对应的解。

第二步，将搜索过程中找到的非支配解保存到外部档案Rep中。此时保存非支配解存在两种情况：若外部档案Rep为空，则直接判断该解是否为非支配解。若该解是非支配解，则将其加入到外部档案Rep中。若外部档案Rep不为空，先判断该解是否为非支配解，如果是非支配解，再判断该解是否不被外部档案Rep中的解支配，如果满足，则将该解加入到外部档案Rep中，然后将被该解支配的其他解删除。

第三步，进行帝王蝶优化算法生成下一代种群。重复以上过程直到满足停止条件。

对于上面第二步存储非支配解的过程，下面进行详细描述。下图1和图2分别是外部档案Rep为空时和不为空时非支配解的存储。

图1 外部档案为空时的存储情况Fig.1 Storage when the external file is empty

图1是外部档案Rep为空时的存储情况，此时直接判断该解是否为非支配解，如果该解不是非支配解，则直接舍弃（如Case1所示），如果该解是非支配解，则直接将该解加入外部档案Rep中（如Case2所示）。图2是外部档案不为空时的情况，此时首先判断该解是否为非支配解，若该解不是非支配解，则直接舍弃（如Case1所示），若该解是非支配解，则需要进一步判断该解是否被外部档案Rep中已有的解支配，若该解被外部档案中的解支配，则舍弃（如Case1所示），若该解不被外部档案中已有的解支配，则将该解加入外部档案Rep中，此时将外部档案中被该解支配的其他解删除。图2的Case2表示外部档案中不存在被该解支配的其他解，则直接将该解加入外部档案Rep中，Case3表示将新解加入外部档案中后，x2和x3被新解支配，此时需要将x2和x3从外部档案中删除。

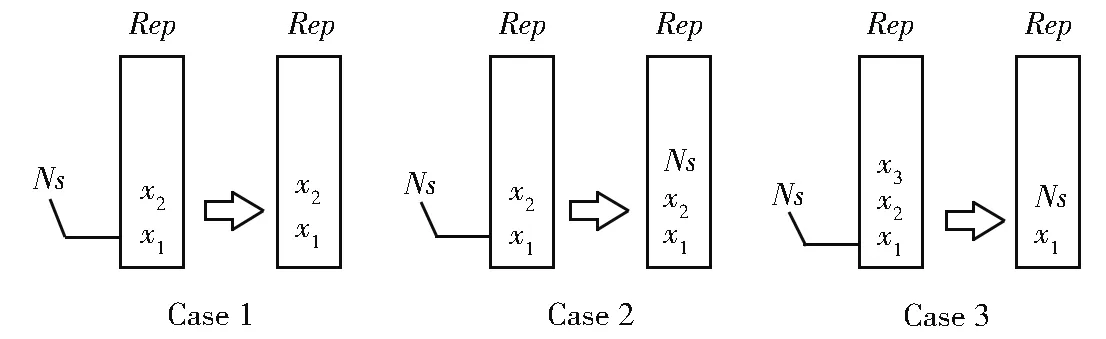
图2 外部档案不为空时的存储情况Fig.2 Storage when the external file is not empty

2.3.2 迁移操作的改进

MBO算法在进行迭代更新时，是将随机选出的个体的相对应维度值直接赋值给新的个体，这样会使种群的多样性受到限制，不利于种群的进化。为此，将差分进化算法［15］和粒子群优化算法中的一些思想加入到MBO算法中，增加种群的多样性。在差分进化算法中，将两个个体相对应维度上的值相减产生一个差分向量，给差分向量分配一个权值后与另一向量相加从而产生变异向量，增加了种群的多样性；粒子群优化算法在进行迭代更新时，会根据个体极值和全局极值进行更新，这样可以加快收敛速度。根据上面的分析，在迁移操作中加入下面的操作：

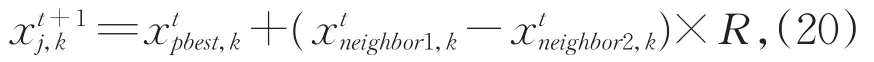
从上式可以看出，R是-1到1之间的随机数，R越大，差分向量对变异向量的影响就越大。

2.3.3 交叉算子

NSGA-Ⅱ采用了快速非支配排序方法，降低了计算的复杂度［16］。在MBO算法中加入NSGA-Ⅱ中的一些操作，可以实现更好的性能。

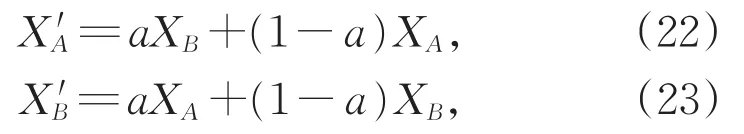
其中，a是-0.5到1.5之间的随机数。进行上面操作可以更好保持种群的多样性。

MBO算法的流程见图3。

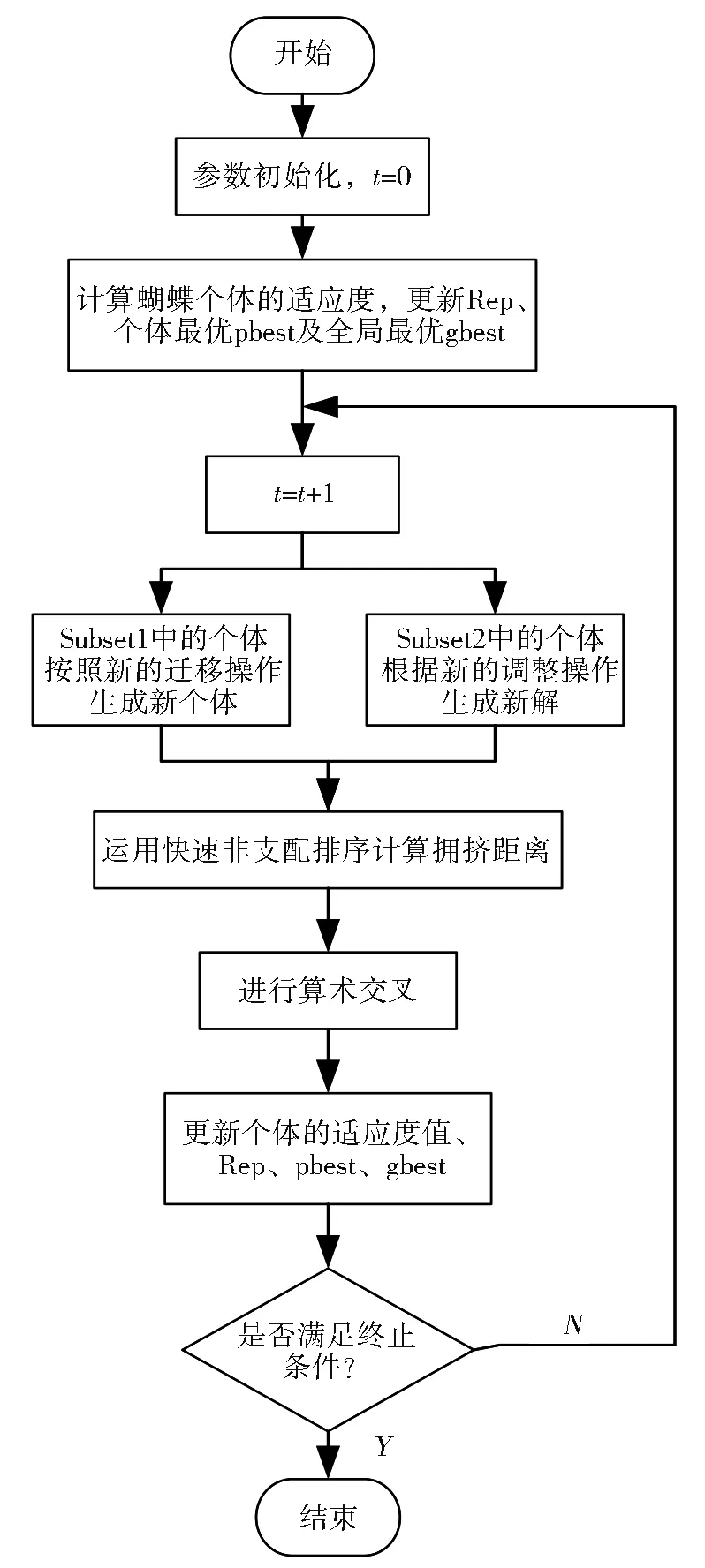
图3 改进的MBO算法流程图Fig.3 Flow chart of improved MBO algorithm

3 实验验证

加工模型规格如表1所示，根据切削手册可以查到刀具的耐磨度系数和切削力系数（表2）。

表1 模型规格Table 1 Model specifications

表2 刀具耐磨系数和切削力系数Table 2 Tool wear coefficient and cutting force coefficient

参照文献［17］，将成本参数Ct设置为60，单位时间所需人工成本C1和管理成本C0之和为2.39元/min，每道工序的换刀时间Tc为2.39 min，辅助时间 Tot是 0.1 min。

将MBO算法在Matlab 2017b中进行仿真计算。种群规模设置为120，进化迭代次数为50次［18］。与相同种群大小和迭代次数的NSGA-Ⅱ算法和PSO进行比较，如图4所示，帝王蝶优化算法具有更好的优化效果。

由图4可以看出，MBO算法比其他智能算法有更好的优化结果。加工时间较短时，生产效率较高，但此时对刀具的磨损严重，因此生产成本较高。延长加工时间后，虽然可以降低对刀具的磨损，但同时也会降低生产效率。当加工时间达到10.3 min后，继续延长加工时间，此时生产成本降低并不明显。

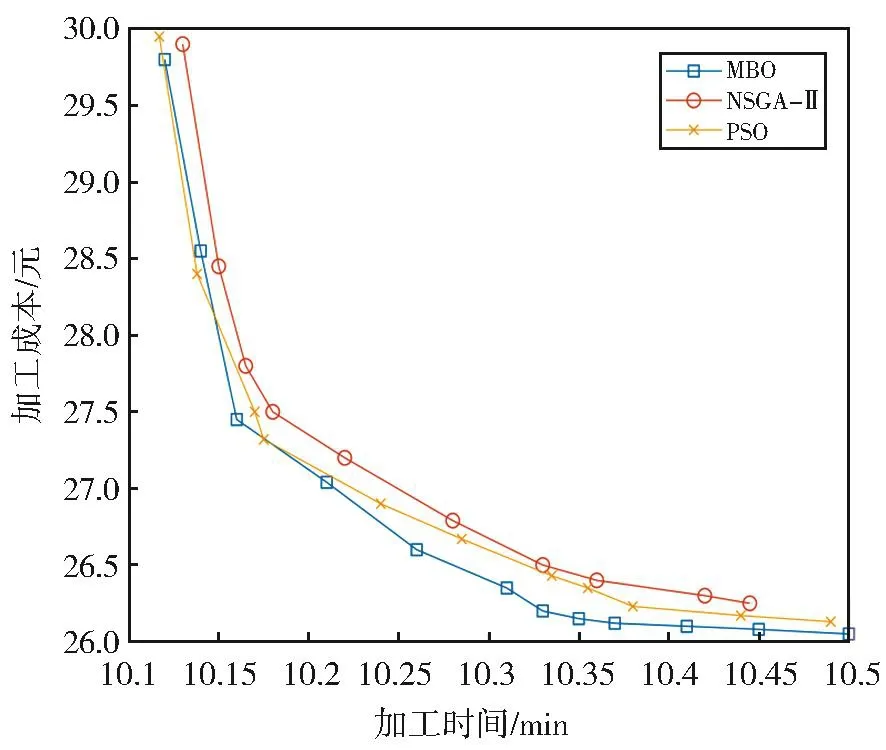
图4 三种算法的Pareto图Fig.4 Pareto diagrams of the three algorithms

采用机电产品再制造综合评价方法对选取较优的六组数据进行分析［19］。该方法为层次分析法。采用逐级细化和层次比较的方式确定权值，然后合成各个子目标对总目标的权值。将加工时间函数和生产成本函数所得值作为准则层，将最优参数结果作为目标层，方案层对准则层的比较矩阵如下：

最大特征值分别为6.07和6.35，取准则层对目标层的权向量为W2=[0.5，0.5]T，一致性指标CI=0，求出T和C最大特征值对应的特征向量，然后归一化处理得到方案层到准则层的权向量W1为：

根据总排序W可以得到最后一组权重最大，由表3和表4可知，当切削速度为12.91 m/min，进给量为0.16 mm/Z时，加工单个零件所需时间为10.41 min，单位成本为26.10元，此时的生产效率和生产成本可以达到较优的值。由此可见，不同的铣削参数对生产效率和生产成本有着重要的影响。

表3 最后五组加工时间（分钟）Table 3 Processing time of the last five groups（min）

表4 最后五组加工成本（元）Table 4 Last five groups of costs（Yuan）

4 结论

本文以最小生产成本和最大生产效率为目标建立了铣削参数的数学优化模型，并且考虑到了实际加工时的限制约束，运用约束违反度的方法进行约束处理。用改进的多目标MBO算法求解优化模型，求得较好的参数组合。通过和其他优化算法比较，表明改进后的MBO算法在进行多目标优化时具有一定的优越性。在实验中发现改进后的MBO算法在接近最优解时有较低概率出现收敛速度过慢的情况，值得进一步研究。