再论“声纳测向精度海上动态测量计算公式”

袁富宇，代志恒，刘 凯，崔 杰

（江苏自动化研究所，江苏 连云港 222061）

0 引言

声纳是水下作战平台的主要探测设备。为保持隐蔽性主要以被动方式接收（探测）目标航行噪声信号，从中提取出目标方位等信息。为保证装备性能，声纳在正式交付使用前都要进行海上测向精度的测量评估，以判断声纳探测精度是否达标。声纳量测精度评估属于量测误差分析与处理范畴［1-3］，包含对随机误差、系统偏差和粗大误差（跳点）的分析处理，其中已知误差序列时随机误差均方根（标准差）的估计方法有Bessel 公式法、Peters 法、极差法、最大误差法和最大残差法。文献［4］描述了一种误差序列未知的随机误差计算公式：“声纳测向精度海上动态测量计算公式”，并对其进行了深入探讨，给出了原公式完整的理论推导，提出了更加精确的计算公式。目前，声纳设备的海上测向评估仍在使用该公式。由于声纳实际测向误差不仅含有随机误差，也常常含有系统偏差，因此，该计算公式已经不再满足声纳量测精度评估的需求了。

本文对该计算公式进行了较为深入的分析，给出了一种改进变形，推广了计算公式适用的试验态势范围；同时也给出一些新的测向精度（随机误差）评估方法，提出了一种存在系统偏差时测向精度评估方案。

1 测向精度计算公式描述及其原理分析

计算公式的试验态势要求：

1）水下观测平台与水面目标船同向匀速直航（平台航向Co=目标航向CT）；

2）观测平台低速航行（Vo=5 kn～7 kn），目标船高速航行（VT=20 kn～25 kn）；

3）目标船起航点比观测平台靠后，以便其通过观测平台大于90°和小于90°的舷角范围；

4）两者航线间距DV=20～30 链（V：Vertical）；

5）同时起航，并确保两者航速稳、航向准；

6）观测平台每10 s 记录一个舷角数据（Qk），共记录n=100 个数据。如图1 所示。

图1 海上测量态势示意图

为了方便证明，作目标船的相对运动如图2 所示。如文献［4］的做法。

图2 目标船相对运动图

OP⊥AM，OP=DV，A、B、C 为目标船的相邻量测点，Q2k-1、Q2k为相邻的两个量测舷角，记两者的差为ΔQ2k-1，即

最终的测向误差均方根为［4］：

其中，A 由式（7）迭代后求出，初值由式（5）计算。

为方便下文比较分析，由计算式（5）、式（6）生成的算法简记为A1，由计算式（7）、式（8）生成的算法简记为A2。

2 测向精度计算公式的分析及改进

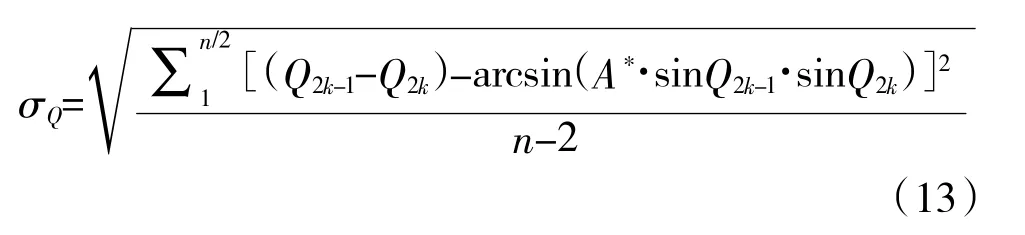
由计算式（12）～式（13）生成的算法简记为A3。

从计算公式的预设态势可以看出，上述计算公式主要是针对舷侧阵或拖线阵而言。对于艇艏阵（圆柱阵、球形阵或者共形阵）而言，上述态势设置就不太合理了，因为艇艏阵的高精度探测区域位于观测平台航向左、右一定角度的扇形区域，最好在量测过程中让目标船经过艇艏，比如让观测平台航向与目标船的航向垂直就可以做到了。如此一来，上述计算公式就不满足要求了。

另一方面，在两者平行航行中，操作者的愿望当然是保持平行，但船舶航向控制机构总是有误差的（航向偏航误差），如期望船只按90°航行，实际上会沿着90.1°方向航行。如果观测平台和目标船的航向同时朝一个方向偏，可能还抵消一些影响，而若两者同时朝外或同时朝内偏，那么对精度估计肯定会有不小的影响。

因此，第2 种改进之处就是允许观测平台和目标船的航向可以不相同，但必须皆匀速直航。

如图3 所示，目标船的相对航向为rCT，相对航速为rVT，观测平台航向为CO。过O 点作rCT的平行线，显见，可以找出无穷多的观测平台、目标船运动参数：CO=rCT，CT=rCT，VT-VO=rCT，满足两者平行航行的要求。实际量测舷角Qk是相对真正CO方向，此时要变换舷角，让其相对目标船的相对航向rCT。变换后的舷角记为Qk'，那么有

图3 非同向时目标船相对态势图

这样一来，就可以把{Qk'}带入到上述系列公式中估计测向量测精度了。由此变换生成的算法简记为A4。

不难看出，上述计算公式的中心思想就是首先估计出相邻舷角差的期望值，之后根据样本方差公式计算出测向精度σQ。依据此思路，还可以通过其他途径计算测向精度σQ。

1）要素解算方法［10-11］

3 存在测向系统偏差时的一种计算方案

在实际应用中发现，声纳测向误差中不仅有随机误差，还存在着不可忽视的系统偏差。声纳测向系统偏差对鱼雷武器的导引效果有着影响，尤其对指控系统中各种目标运动要素解算算法有着“要命”的影响。因为目前指控系统中大多数要素解算算法都是基于极大似然估计原理推得的，对于白噪声量测误差往往能够达到其最优精度，而对于含有系统偏差的量测误差其表现往往很差。目前数理统计中各种估计方法常是建议先去除掉量测中的系统偏差（从产生源头去除、或估计出来等等），而后再套用各种估计方法去实际应用。

因此，对于声纳测向误差，不仅要考察其随机误差，而且还要考察其系统偏差。实际装备中不可能没有一点系统偏差，而是能否限制其在一定范围内，以满足指控系统的应用要求。

易见，第1 节、第2 节描述的测向精度计算公式（方法）估计不出系统偏差，因为相邻舷角之差ΔQ2k-1中已基本不含有系统偏差（假定系统偏差光滑变化），因此，有必要考虑其他的途径。下面给出一种方案，在目前试验条件下是能够做到的，大致有以下几个步骤（都是事后处理）：

几点说明：

1）关于“精确”方位Bk的计算

式（20）中的（xTk，yTk）和（xOk，yOk）分别表示在量测时刻tk目标船和观测平台的位置坐标，其值可以由两者的北斗导航信息精确地计算出来，因为目前北斗导航信息的后期处理可以达到厘米级精度，可以认为Bk没有误差。

4）关于系统偏差的评估

可以有3 种方式，第1 种是把随机误差和系统偏差综合起来考察，此时

第3 种方式随机误差和系统偏差分开考察，但对系统偏差不仅考察其最大、最小值，还要考察其变化过程，即绘制出所有有效航次的系统误差曲线（随量测时刻变化）。这是指控系统最为关注的一种方式。

4 仿真验证与分析

4.1 仿真态势选择与误差仿真

对于测向误差的仿真，随机误差和系统偏差分开独立仿真叠加到舷角真值上。对于舷侧阵和拖线阵来说，系统偏差随着方位线与阵垂线夹角的增大而增大，呈现某种非线性变化（变化系数为δ）；对于圆柱阵或球形阵来说，系统偏差随舷角Qk的（绝对值）增大而增大，近似呈现线性变化（变化系数为ρ）。

实际上，随机误差也不是恒定不变的，它会随着目标船的距离而变化，也会随着上述两个角度（绝对值）的增加而增加。由于变化规律复杂，为简单起见，声纳测向精度指标按距离和角度划分不同的区域，在每一区域内认为随机误差服从相同的分布。因此，在仿真中假定随机误差均方根σQ是常数，随机误差服从高斯分布N（0，σQ2）。

对于舷侧阵，取σQ=0.1°～1°；对于拖线阵，取σQ=1°～4°；对于圆柱阵，取σQ=0.1°～0.7°。

4.2 无误差时的验证

仿照文献［4］，先考察没有误差时各计算公式/方法的表现，选择文献［4］建议的验证态势（针对舷侧阵和拖线阵设计的态势），总时间T=1 000 s（dt=10 s），结果单位为度（下同）。

从理论上讲，当没有任何误差时表1 中的所有σQ=0。但由于方法的近似性使得其中的方法A1、A6、A7、A8的估计值并不接近零。

表1 无误差时的验证结果

4.3 随机误差计算验证

当舷角叠加有随机误差时，对于各种计算方法的考察，不能仅观察一个航次的结果，应该多观察几个航次，统计计算其平均值和二次原点矩。记EσQ表示估计误差均方根均值，σσQ表示估计误差均方根的原点矩均方根，即

N 为设定的航次数，本文取N=10 000，rσQ为舷角误差均方根真值。

1）舷侧阵验证

DV=30 链，CO=CT=π/2，量测间隔取dt=10 s（量测点数n=100）和dt=1 s（（量测点数n=1 000）。当σQ=0.5°时，计算结果如下页表2 所示。

表2 σQ=0.5°时舷侧阵统计结果

当σQ=1°时，计算结果如表3 所示。

表3 σQ=1°时舷侧阵统计结果

2）拖线阵验证

取DV=300 链，其余量取值同上。当σQ=2°时，计算结果如表4 所示。

表4 σQ=2°时拖线阵统计结果

3）圆柱阵验证

取DV=100 链，CT=π/2，CO=0，量测间隔取dt=10 s（量测点数n=100）和dt=1 s（量测点数n=1 000）。当σQ=0°时，计算结果如表6 所示。当然，在这种交叉航次态势下，方法A1～A3都不再适用，其余方法理论上仍适用。仍放在一起考察，看一下A1～A3竟有多不适用。

表6 无任何误差时dt=10 s 及dt=1 s 时圆柱阵计算结果

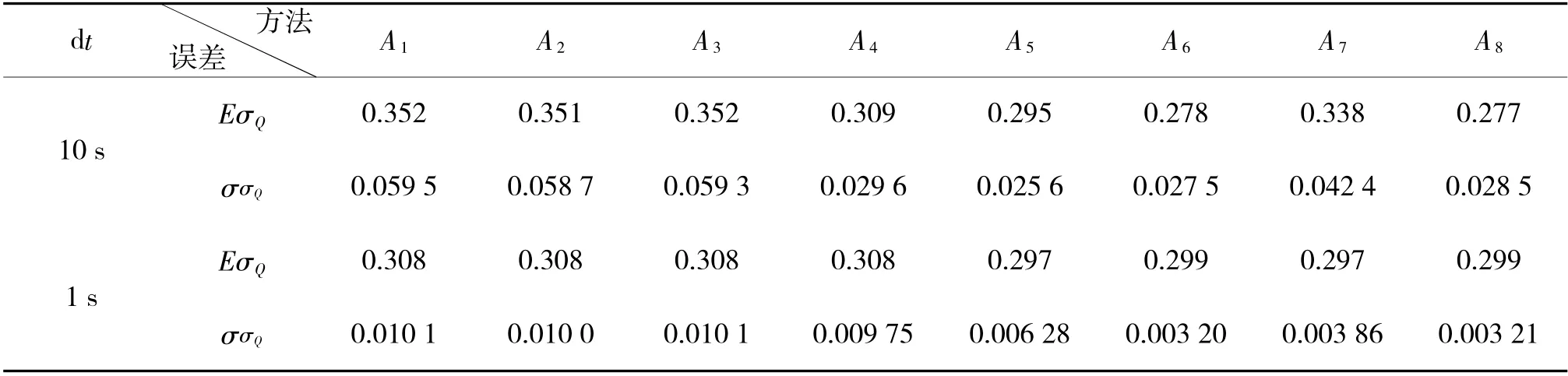
表7 σQ=0.3°时圆柱阵计算结果

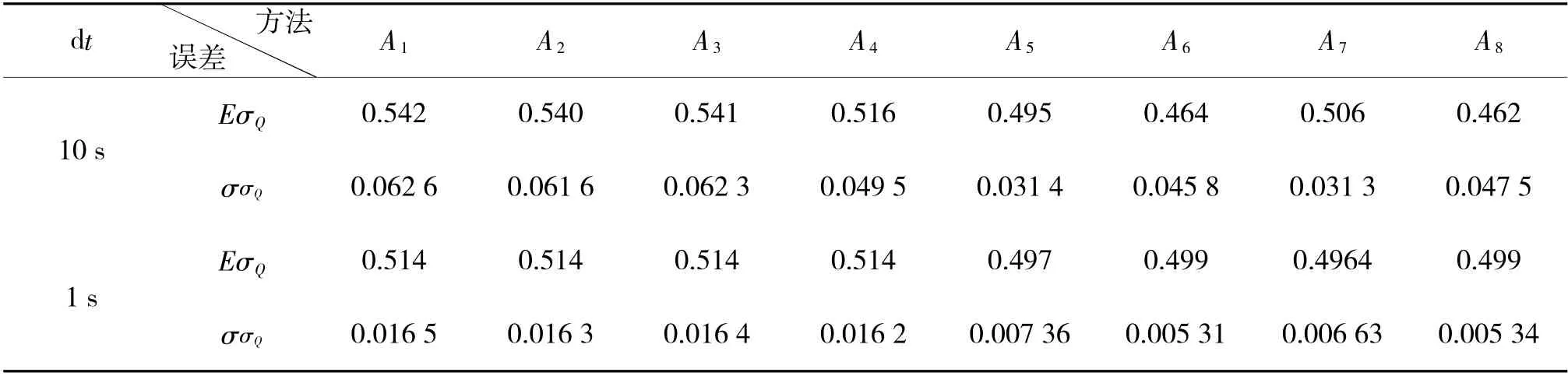
表8 σQ=0.5°时圆柱阵计算结果

4）结果分析

先看舷侧阵和拖线阵的验证结果。从表2～表5 可以看出，文献［4］给出的两种计算方法A1、A2及其本文给出的改进方法A3（此时A3、A4等价），其测向随机误差的估计是有偏的：当量测点数n=100（dt=10 s）时，σQ=0.5°的偏差期望值约为0.016°，二阶原点矩均方根约为0.05°；σQ=1°的偏差期望值约为0.031°，二阶原点矩均方根约为0.099°；σQ=2°的偏差期望值约为0.062°，二阶原点矩均方根约为0.198°；σQ=4°的偏差期望值约为0.13°，二阶原点矩均方根约为0.397°。当量测点数n=1 000（dt=1 s，总时间不变）时，σQ=0.5°的偏差期望值约为0.014°（与0.016°相比改进不大），二阶原点矩均方根约为0.016°；σQ=1°的偏差期望值约为0.028°（与0.031°相比改进不大），二阶原点矩均方根约为0.032 5°；σQ=2°的偏差期望值约为0.056°（与0.062°相比改进不大），二阶原点矩均方根约为0.065°；σQ=4°的偏差期望值约为0.112°（与0.13°相比改进不大），二阶原点矩均方根约为0.13°。

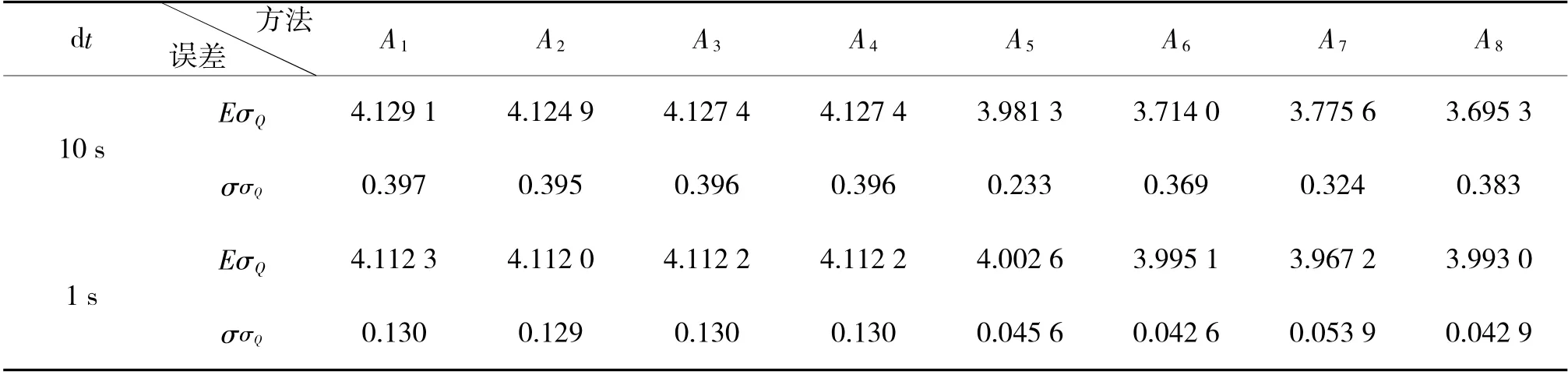
表5 σQ=4°时拖线阵统计结果

本文提出的4 种新方法A5（要素解算方法，基于极大似然估计）、A6（多项式拟合方法）、A7（小波滤波方法）和A8（非参回归法），当n=100 时，A6、A7和A8的估计误差（包括期望值与二阶原点矩均方根）都很大，A5方法估计效果最好（比A1、A2和A3），期望值接近真值，但二阶原点矩均方根还不够小。当n=1 000 时，A5～A8表现都比方法A1～A3好，不论是期望值或是二阶原点矩，其精度都高出1～2 个数量级。其中方法A6和A8效果最好。

再看圆柱阵的验证结果。由于选取了航线交叉态势，从原理上方法A1～A3已经不适用于此情形。从表6～表9 可看出，即使不迭加任何误差（表6），A1～A3的估计结果也不为0（约为0.17°（n=100）和0.017°（n=1 000））；添加误差时，n=100 的估计值也有0.04°～0.05°的偏差，而改进的算法A4则表现良好。此时本文提出的方法A5仍然表现优异（相对A1～A3）。当n=1 000 时，A1～A4表现趋同（这倒与直观不符）。此时A5～A8表现都很好，精度远超方法A4：均值更接近真值，二阶原点矩更小。

表9 σQ=0.7°时圆柱阵计算结果

从以上分析可以看出，文献［4］的测向精度计算方法（包括本文改进的）A1～A4，原理上是正确的，但对于高精度测向误差评估来讲还是稍显粗糙；本文提出的4 种新途径（A5～A8）效果更好些，尤其在增加量测点的条件下。对于圆柱阵的测向误差评估，提出了改进方法A4，在n=100 时效果好于A1～A3，而当n=1 000 时A1～A4效果也趋同，但都逊于A5～A8。因此，在进行声纳测向随机误差评测时建议加大量测点数（如n=1 000）以提高估计精度，同时建议选用本文提出的新方法A5～A8，因为文献［4］的方法A1～A3有估计偏差。

4.4 系统偏差估计验证

仅采用第3 节推荐的计算方案，因为上述方法只能估计随机误差：A1～A3方法中相邻舷角之差已把系统偏差减掉，剩下的ΔQk中不含有系统偏差信息；A5～A8方法中系统偏差要么作为低频信号也被减掉，要么被拟合入回归系数中，最终也被减掉。观察如下算例。

针对舷侧阵，取σQ=1°，并迭加上系统偏差，A1～A8统计结果如下（n=1 000，N=10 000）：

表10 存在系统偏差时上述各方法的估计期望

4.4.1 舷侧阵例子

取σQ=1°，系统偏差系数δ=0.02。随机误差加上系统偏差的综合误差σ=1.159 179°。

表11 说明：

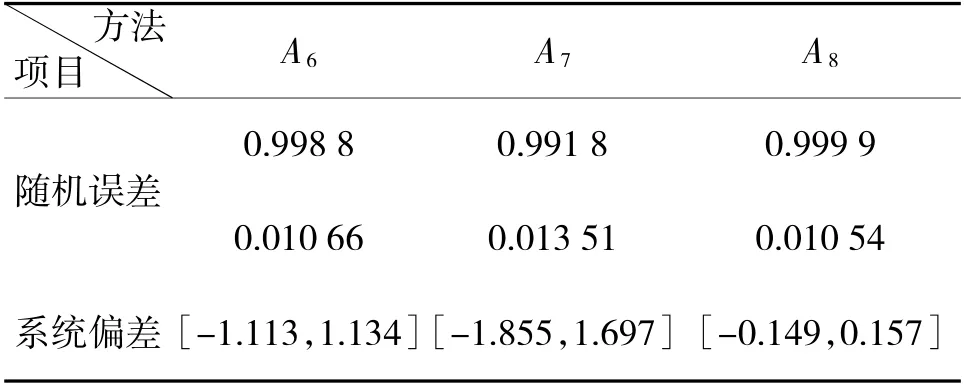
表11 方法A 6～A 8 的随机误差估计及系统偏差估计误差区间

1）随机误差栏目中对应每一方法的上格数值表示估计期望值，下格数值表示估计的二阶原点矩均方根；

2）系统误差栏目中对应每一方法的估计误差区间，是从n×N 个差值（每一时刻系统偏差估计值减去仿真迭加的系统偏差真值）寻找出的最小值和最大值。

下面给出方法A6～A8估计的系统偏差过程值，每隔10 s 挑选出一个，包括首尾两时刻的值。

图示说明：图4、图6、图8 的纵坐标表示舷角系统偏差差值（各方法系统偏差估计值与系统偏差真值之差）绝对值之均值（单位：°），横坐标为量测舷角点数；图5、图7、图9 的纵坐标表示舷角系统偏差差值的均方根（单位：°），横坐标为量测舷角点数。

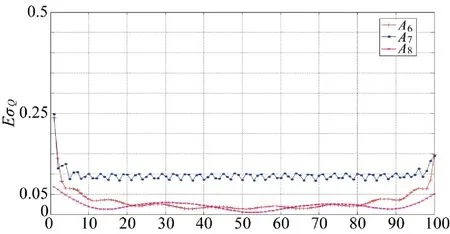
图4 舷侧阵算例舷角系统偏差估计误差绝对值均值曲线

图5 舷侧阵算例舷角系统偏差估计误差均方根曲线

4.4.2 拖线阵例子

取σQ=4°，系统偏差系数δ=0.03。随机误差加上系统偏差的综合误差σ=4.095 033°。如下页表12 所示。

表12 方法A 6～A 8 的随机误差估计及系统偏差估计误差区间

表中各项含义同表11。

方法A6～A8估计的系统偏差过程值（均值、均方根）如图6、图7 所示（每隔10 s 挑选出一个，包括首尾两时刻的值）。

图6 拖线阵算例舷角系统偏差估计误差绝对值均值曲线

图7 拖线阵算例舷角系统偏差估计误差均方根曲线

4.4.3 圆柱阵例子

取σQ=0.7°，系统偏差系数ρ=0.013 33，ΔQ0=0.4°（系统偏差=ρ·Q+ΔQ0）。随机误差加上系统偏差的综合误差σ=1.150 254°。

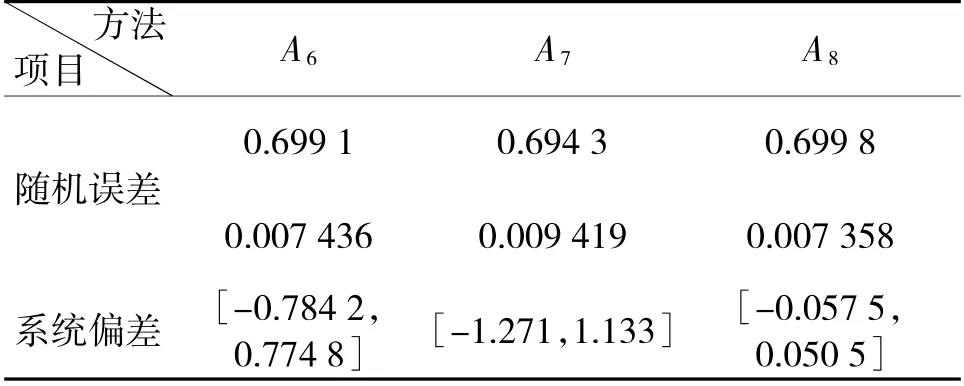
表13 方法A 6～A 8 的随机误差估计及系统偏差估计误差区间

表中各项含义同表11。

方法A6～A8估计的系统偏差过程值（均值、均方根）如图8、图9 所示（每隔10 s 挑选出一个，包括首尾两时刻的值）。

图8 圆柱阵算例舷角系统偏差绝对值均值曲线

图9 圆柱阵算例舷角系统偏差差值均方根曲线

4.4.4 结果分析

当舷角量测次数n=100 时，三阵估计结果都不好，导致结果不太可信（因此，没有展现结果）。

当n=1 000 时，3 种方法A6～A8的随机误差估计效果很好，表现在随机误差估计期望与真值相差很小，二阶原点矩均方根也很小，精度较高符合实际需求。对于系统偏差估计，A8（非参回归方法）效果最好，表现在误差区间小，各时刻的估计误差（绝对值）期望及相应二阶原点矩均方根都很小，“两头翘”（边界误差偏大）的幅度很小。另外两种方法A6（小波）和A7（多项式）效果较差（每时刻的估计误差期望及二阶原点矩均方根偏大），尤其是系统偏差的估计误差区间降不下来。

也不难发现，随着σQ增大，相应的估计精度，尤其是系统偏差的估计精度会下降。因此，对于大误差情形，建议增加量测次数以提高估计精度。

5 结论

本文对目前工程中仍在使用的一种声纳测向精度计算公式进行了更进一步的分析讨论，推广了这种公式，使之能够适用交叉航行试验态势，以满足艇艏圆柱阵/球形阵的精度测试。同时提出了几种新的计算方法，仿真结果表明，原有的计算公式是有偏的（即使增加量测点数也降不下来），而新方法是渐近无偏的，即量测点数越多，估计精度越高。

针对存在系统偏差情形，提出了一种计算途径。仿真试验表明上述方法仅能估计随机误差，而新的计算途径不仅能精确估计随机误差，也能较准确地拟合出系统偏差。

为满足指控系统对测向误差的要求，建议声纳测向的随机误差和系统偏差各自单独进行测试评估，同时建议增加观测平台在转向机动段的这两项误差评估指标，因为1 min～2 min 的机动段的测向信息对于武器导引尤其是缩短目标运动要素解算时间及提高解算精度至关重要。