基于多尺度卷积神经网络的结构损伤识别研究

张健飞，蔡东成

（河海大学力学与材料学院，江苏 南京 210098）

引言

工程结构在服役期间，由于受到环境侵蚀、材料老化、疲劳效应和自然灾害等因素作用，将会不可避免地产生损伤累积，一旦关键构件的损伤累积到一定程度，将会导致结构破坏。因此，为了能够保证结构性能、延长结构寿命，需要及时发现结构损伤并进行维修处理。基于振动的结构损伤识别方法利用结构的动力测试信号进行结构整体损伤状况检测，且检测期间不需要中断结构的使用，相较于传统的无损损伤检测方法具有很大的优越性［1］，但是在实际应用过程中，会不同程度地遇到易受环境影响、模型依赖性强、系统容错性差等问题的困扰。人工神经网络最初用于模拟人的大脑功能，它由大量相互连接的简单神经处理单元组成，可以不依赖于模型，具有较强的容错性和鲁棒性以及学习联想能力等特征，因而在结构损伤识别领域受到了广泛的关注。人工神经网络用于结构损伤识别的基本原理就是通过建立特征参数与结构的损伤状态之间的输入输出映射关系来实现损伤识别，目前已经构建了许多结构动力特征作为神经网络的输入参数，如：固有频率［2］、振型［3］、模态曲率［4］和加速度二次协方差［5］等。然而这些人为设计的特征参数并不一定是最优的，不可能在所有类型的损伤识别中都取得最优效果，以卷积神经网络为代表的深度学习网络可以直接从原始信号中提取最优的特征，从而最大程度上提高识别准确率［6］。

卷积神经网络（convolutional neural networks，CNN）是一类受生物视觉感知机制启发而建立的深度学习代表性网络结构，其研究始于20世纪80至90年代，最早出现的经典卷积神经网络是LeNet-5［7］。由于卷积神经网络的局部连接、权值共享及池化操作等特性使之可以有效地降低网络的复杂度，减少训练参数的数目，使模型具有强鲁棒性和容错能力，且易于训练和优化网络结构，卷积神经网络已经在计算机视觉、语音识别等领域得到了广泛应用［8］。在结构损伤识别领域，近年来卷积神经网络也得到较多研究和应用。罗雨舟等［9］通过有限元数值模拟试验提取结构多点加速度信号组成矩阵，搭建卷积神经网络模型对该加速度矩阵进行特征提取并实现损伤诊断，研究了结构在不同激励类型作用下和不同噪声强度下的损伤诊断精度。李雪松等［10］以IASC-ASCE SHM Benchmark 结构的数值模拟数据为研究对象，用卷积神经网络直接从加速度信号自动提取特征，并与小波包频带能量、本征模态函数能量特征对比，分析卷积神经网络提取特征的有效性，同时提出混合噪声训练模式，加强特征抗噪能力，取得了良好的识别效果。李书进等［11］以多层框架结构节点损伤位置的识别问题为研究对象，构建了可以直接从结构动力反应信号中进行学习并完成分类诊断的基于原始信号和傅里叶频域信息的一维卷积神经网络模型和基于小波变换数据的二维卷积神经网络模型。何浩祥等［12］将车桥耦合振动下的原始结构响应信号进行小波包滤波和重构，通过递归分析获取不同损伤工况的递归图，将其作为卷积神经网络的输入，提出基于卷积神经网络和递归图的桥梁结构损伤识别计算流程和方法。Khodabandehlou等［13］将一座钢筋混凝土公路桥缩尺模型振动台试验测得的加速度数据组成的矩阵作为输入，采用二维卷积神经网络对结构损伤进行识别，取得了很好的识别效果，并检验了网络对微小损伤的鲁棒性和敏感性。Lin等［14］采用卷积神经网络从简支梁有限元模拟生成的加速度数据中提取损伤特征，在有噪声情况和多损伤情况下都取得了很高的损伤识别精度，同时通过隐层可视化对所提取的特征进行了物理解释。Liu 等［15］将传递函数和一维卷积神经网络相结合对结构损伤识别方法进行了研究，并以ASCE Benchmark 结构动力响应的传递函数作为卷积神经网络的输入数据，对方法的有效性进行了验证，通过与时间序列和FFT数据相比较，显示了传递函数数据中获取的特征具有更高的损伤敏感性。

实际结构的动力响应中通常包含多阶模态成分，而且外界激励通常也在不断变化，因此振动信号在不同时间尺度上具有不同的特征。传统卷积神经网络由于采用固定尺寸的卷积核，缺乏多尺度特征提取能力，难以捕捉到动力信号中的多尺度特征。为此，多尺度卷积神经网络开始得到关注。Jiang 等［16］针对风机齿轮箱振动信号的多尺度特征，通过对原始信号施加不同尺寸窗口的滑动平均操作，得到表征不同尺度的信号，并作为卷积神经网络的输入，获取不同尺度上的特征信息，提升了齿轮箱故障诊断的性能。Liu 等［17］针对发动机在不同运行状态下振动信号的多尺度特性，提出了一种采用多尺度卷积核的卷积神经网络，并通过实测数据验证了方法的有效性和优良性能。Zhang等［18］首先采用具有不同尺寸卷积核的一维卷积神经网络对振动信号进行处理，然后将处理结果连接形成二维矩阵作为二维卷积神经网络的输入数据，减少了网络层数，提高了在小样本情况下机械故障分类精度。

文中通过对振动信号下采样、滑动平均和采用不同尺寸卷积核的策略实现了3个多尺度卷积神经网络，并将之应用于结构的损伤识别，通过数值试验和振动台试验，验证了方法的有效性，较之单一尺度的卷积神经网络，取得了更好的损伤识别效果。

1 卷积神经网络

卷积神经网络主要由卷积层、池化层和全连接层组成，其基本结构如图1所示。卷积层的作用是从输入数据中学习其内在的特征表示，卷积层由一系列卷积核组成，用于计算不同的特征图，每一个特征图在生成时，卷积核对于输入来说是共享的，使用不同的卷积核就得到不同的特征图。特征图中的每一个神经元跟上一层的某一个区域的神经元相互连接，这部分区域被称为神经元在上一层的感受野。特征图的计算一般包含2步：首先利用卷积核对输入数据进行卷积操作，然后对每个卷积计算结果施加非线性函数。第l层第k个特征图中（i，j）位置处的数值计算如式（1）所示，

图1 卷积神经网络的基本结构Fig.1 Basic structure of the CNN

典型的激活函数有sigmoid、tanh和ReLU等。

池化层的作用是对卷积层中提取的特征进行汇总并对信息进行压缩，从而使卷积神经网络能够抽取的特征范围更广。池化层通常位于2 个卷积层之间，池化层的每一个特征图与它前面的卷积层相关联。记池化函数为pool( · )，则对于每一个特征图，可以得到

式中，ℜij为（i，j）周边的邻近区域，常见的池化操作有取平均值和取最大值。

在经过多个卷积和池化操作之后，卷积神经网络已经完成了输入信号的特征提取和压缩。在卷积神经网络结构中，经多个卷积层和池化层后，连接着1 个或1 个以上的全连接层，将前一层的所有神经元与该层的每一个神经元相连接，以获取全局信息。卷积神经网络的最后一层全连接层的输出值被传递给一个输出层，通常采用softmax逻辑回归进行分类，该层也可称为softmax层。

卷积神经网络的训练是一个全局优化问题，令θ代表卷积神经网络的所有参数（权值向量和偏移值），N个输入-输出数据对记为{ (x(n),y(n));n∈[ 1,2,…,N]}，其中x(n)为第n个输入数据，y(n)是与第n个输入数据相应的标记值。o(n)为卷积神经网络的输出值，则卷积神经网络的损失函数可以表示为，

通过最小化损失函数，可以得到参数的最优值，随机梯度下降法是常用的卷积神经网络优化方法。

2 多尺度卷积神经网络的实现

多尺度卷积神经网络的主要思想是将多尺度特征学习能力融入传统卷积神经网络，文中采用2 种做法实现多尺度卷积神经网络：一种是对输入的振动信号进行多尺度处理；另一种是在卷积神经网络中采用多尺度卷积核。

第1种做法就是采用固定尺度的卷积核，但是对输入的振动信号进行多尺度处理。设振动测试得到的振动加速度信号为x={ }x1,x2,…,xN，其中xi为时刻点i的加速度值，信号中共有N个时刻点，即信号长度为N。然后对振动信号进行粗化，构建具有不同尺度特征的振动信号序列，粗化的策略主要有下采样和滑动平均两种方式。

下采样就是对振动信号序列间隔s个样值取样一次，这样得到新序列就是原序列的下采样，如式（5）所示。

滑动平均就是以宽度为s的窗口在原始振动信号上以s为间隔滑动，对窗口内的数据进行平均运算，如式（6）所示。

对振动信号进行下采样或者滑动平均后就得到不同尺度的振动信号，然后将这些信号并行地输入分支卷积神经网络进行卷积和池化运算，再将各个分支卷积神经网络的输出合并为一个融合多尺度特征的向量作为全连接层的输入，最后由softmax层输出损伤识别结果，如图2所示。图中原始信号处理成3种不同尺度的信号，其下采样间隔（或者滑动窗口宽度）s分别等于s1、s2和s3。由于各分支卷积神经网络对不同尺度的振动信号进行处理采用相同的卷积核大小，从而使得大尺度信号的感受野要比小尺度信号来的大，这样不同的卷积神经网络就提取到了不同尺度的特征。

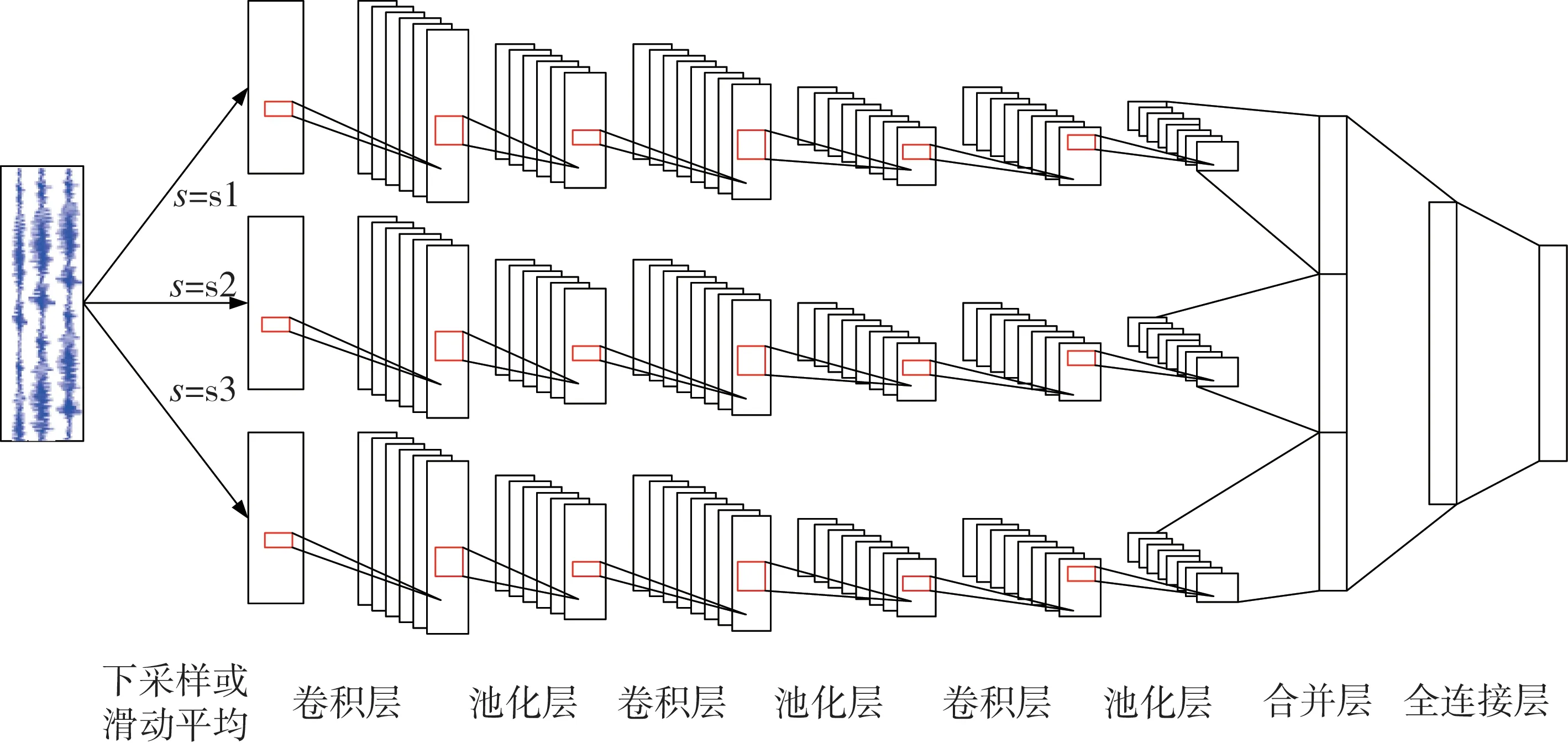
图2 多尺度输入卷积神经网络Fig.2 Structure of multi-scale CNN with multi-scale inputs

第2 种实现多尺度卷积神经网络的做法就是在卷积运算中采用多种不同尺度的卷积核，从而实现对振动信号多尺度特征的提取。通过多个采用不同尺度卷积核的分支卷积神经网络提取信号的不同尺度特征，然后将这多个卷积神经网络的输出合并为一个融合多尺度特征的向量作为全连接层的输入，最后由softmax层输出损伤识别结果，如图3所示。图中采用3个不同尺度卷积核的分支卷积神经网络，卷积核尺寸分别为于s1×t1、s2×t2和s3×t3。

图3 多尺度卷积核卷积神经网络Fig.3 Structure of multi-scale CNN with different kernel sizes

为了下文描述方便，分别将下采样、滑动平均和多尺度卷积核这3 个多尺度卷积神经网络记为MSCNN1、MSCNN2和MSCNN3，将单一尺度卷积神经网络记为SSCNN。

3 试验验证

3.1 网络结构和参数

卷积神经网络的结构和参数对其性能具有很大的影响，文中通过大量的试验，选定了较优的卷积神经网络结构和参数。MSCNN1、MSCNN2 中下采样间隔（滑动平均窗口宽度）s=1，2，4 即包含3 个分支卷积神经网络。每个分支卷积神经网络采用相同的固定尺寸卷积核，包含3 个卷积层和池化层，第1 层包含8个32 × 3 卷积核的卷积层和4×1 的池化层；第2 层是16 个32×3 卷积核的卷积层和4×1 的池化层；第3 层是32 个32×3卷积核的卷积层和4×1的池化层。然后将各个分支卷积神经网络的输出合并为一个向量作为全连接层的输入，最后连接输出层，输出层的神经元个数对应损伤模式的个数，每个神经元输出对应不同损伤模式的发生概率，如图2所示。

MSCNN3中的卷积神经网络采用不同尺度卷积核，包含3个采用不同尺寸卷积核的分支卷积神经网络。每一个分支卷积神经网络包含3 个卷积层和池化层，第1 层包含8 个卷积核，紧接着4×1 的池化层；第2 层是16 个卷积核，紧接着4×1 的池化层；第3 层是32 个卷积核，紧接着4×1 的池化层。第1 个分支卷积神经网络的卷积核尺寸为8×3，第2个分支卷积神经网络的卷积核尺寸为32×3，第3 个分支卷积神经网络的卷积核尺寸为128×3。然后将各个分支卷积神经网络的输出合并成全连接层的输入向量，最后连接输出层，输出层的神经元个数对应损伤模式的个数，每个神经元输出对应损伤模式的发生概率，如图3所示。

为了比较和分析多尺度卷积神经网络的性能，文中以单尺度卷积神经网络作为基准，单尺度神经网络同样包含3个卷积层和池化层，第1层包含8个32×3卷积核的卷积层和4×1的池化层；第2层是16个32×3卷积核的卷积层和4×1的池化层；第3层是32个32×3卷积核的卷积层和4×1的池化层，并将其输出作为全连接层的输入；最后由输出层输出各个损伤工况的发生概率。

网络中除了全连接输出层的激活函数为softmax，其余各层的激活函数均为ReLU。为了防止过拟合，在全连接层的后面插入一个丢弃层（Dropout）［8］，丢弃概率为0.5。训练时设置批尺寸为64，训练总批数为30次，训练时保存最优模型用于损伤识别。

3.2 数值试验

3.2.1 悬臂梁

文中首先建立了一个悬臂梁有限元模型进行数值试验，悬臂梁材质为钢材，长1 200 mm，方形截面尺寸为20 mm×20 mm，底部为固定端，顶部为自由端。在悬臂梁一侧不同高程处分别设置深2 mm的水平裂缝（记为C1～C6）模拟不同位置的损伤（截面损伤程度为10%），另一侧设置7个测点（记为m1～m7）记录悬臂梁水平向加速度，悬臂梁裂缝位置和测点位置如图4所示。每个损伤工况为不同位置处的单个裂缝，如表1所示。

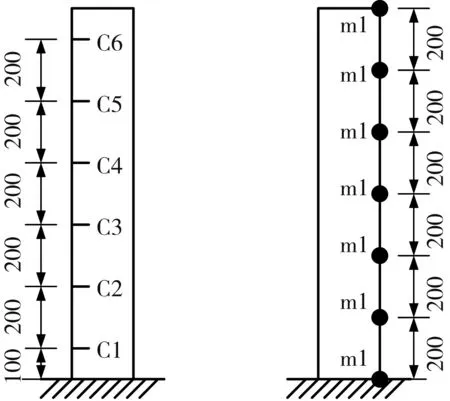
图4 数值试验中悬臂梁裂缝位置和测点图（单位：mm）Fig.4 Positions of the cracks and accelerometers on the cantilever beam in numerical test（unit：mm）

通过在悬臂梁底部施加水平向白噪声加速度模拟环境激励，有限元计算时间步长取为0.000 1 s，采用Rayleigh 阻尼。按照表1 所示的损伤工况，生成7 个测点上7 种不同损伤工况的时长为30 s 的加速度响应信号序列，每个序列包含300 000 个时刻点，即每种损伤工况可得到一个300 000 × 7 的加速度信号矩阵。然后从每个信号矩阵中随机抽取1 000 个大小为1 024 × 7 的子矩阵作为卷积神经网络的输入样本矩阵，共得到7×1 000=7 000 个样本矩阵。将样本按照7∶2∶1 的比例划分，分别作为卷积神经网络的训练集、验证集和测试集，训练集和验证集用于网络的训练，测试集用于测试网络的泛化性能。

表1 数值试验中悬臂梁的损伤工况Table 1 Damage cases of the cantilever beam in numerical test

在实测信号中，噪声总是存在的，这些噪声一般可以假设为符合高斯分布的白噪声［19］。文中在有限元计算所得的各测点加速度信号中加入白噪声数据来模拟实测信号，即：

图5 给出了单尺度卷积神经网络和多尺度卷积神经网络在本例数据集上的训练曲线，限于篇幅只给出了在无噪声数据集beam-n00 上的曲线，图中横坐标为训练批次，纵坐标为准确度和损失函数。可以看出：单尺度卷积神经网络在本例数据集上未能收敛，且验证集上的损失函数不下降、准确率也不提高，存在过拟合的现象。而多尺度卷积神经网络最终都收敛到理想水平，准确率接近100%，训练集和验证集上的训练曲线基本吻合，未出现过拟合现象。表2给出了各个网络在不同噪声水平下训练集和验证集上的准确率，可以看出：随着噪声水平的提高，各个网络在训练集和验证集上的准确率均有所下降，当噪声水平达到5%时，验证集上准确率明显低于训练集，说明网络泛化性能也在下降。

表2 卷积神经网络在悬臂梁数值试验数据上的训练准确率Table 2 Training accuracy of the CNNs on data from numerical test of cantilever beam

图5 卷积神经网络在悬臂梁数值试验数据上的训练曲线Fig.5 Training curves of the CNNs on data from numerical test of cantilever beam

为了进一步检验多尺度卷积神经网络的泛化性能，文中在测试集的每一种损伤工况中随机抽取了100个样本，用于测试各个网络的损伤识别性能。表3给出了各个网络在测试集各个损伤工况上的识别性能，可以看出：根据概率最大损伤判别法则，单尺度卷积神经网络在本例数据集上未能准确识别出损伤工况，这与训练曲线的结论是一致的；各个多尺度卷积神经网络虽然随着噪声水平的提高，识别精度不断下降，但仍然都能准确识别出7种不同的损伤工况，具有较好的抗噪性。

表3 卷积神经网络在悬臂梁数值试验测试集上的损伤识别概率Table 3 Damage identifying probability on test data set from numerical test of cantilever beam

3.2.2 钢框架

为了检验文中方法对于较为复杂结构的有效性，建立了一个两跨钢框架有限元模型，该框架由2根纵梁和7 根横梁刚性连接而成，纵梁和横梁采用相同的工字型截面，截面积和惯性矩分别为1.054 × 10-3m2和1.039 × 10-6m4，如图6 所示。在结点A、H处采用铰支座与基础相连接，D、G、K和N结点处为辊轴支座。在B、C、E、F、I、J、L、M结点上设置测点记录竖向加速度。损伤工况模拟了实际桥梁工程中常见的一些病害：基础沉降引起的支座脱空、锈蚀老化引起的支座活动受限和螺栓松动引起的结点连接失效等，如表4 所示。

图6 数值试验中钢框架结构图Fig.6 Structure layout of the steel frame in numerical test

表4 数值模拟中钢框架的损伤工况Table 4 Damage cases of the steel frame in numerical test

在结点B处施加竖向白噪声随机荷载激励，分别对表4所示的损伤工况进行有限元模拟，计算时间步长取为0.002 s，采用Rayleigh 阻尼。在8 个测点上生成6 种不同损伤工况的加速度响应信号序列，记录时长为500 s，即每种损伤工况得到一个250 000×8 的加速度信号矩阵。然后从每个信号矩阵中随机抽取2 000 个大小为256×8 的子矩阵作为卷积神经网络的输入样本矩阵，共计6×2 000=12 000 个样本矩阵。为了模拟实测信号中的噪声影响，样本中加入2%和5%水平的噪声，再按照7∶2∶1 的比例，将样本划分为训练集、验证集和测试集，分别将含有0%、2%、5%噪声的数据集记为frame-n00、frame-n02和frame-n05。

各个网络在不同噪声水平下训练集和验证集上的准确率如表5所示，可以看出：在本例数据上单尺度网络的训练准确率随着噪声水平增大而下降较快，多尺度网络的训练准确率均高于单一尺度网络，达到95%以上。表6给出的是各个网络在测试集各个损伤工况上的识别性能，可以看出：虽然各个卷积神经网络在本例数据集上均能准确识别出损伤工况，但是多尺度网络的识别精度要更高一些，具有较强的抗噪性。从各个损伤工况的识别精度可以看出：损伤工况1、2、3 的识别精度明显高于损伤工况4、5，说明本例中损伤工况1、2、3对结构动力特性的影响程度要大于损伤工况4、5，从而相对更容易被识别。

表5 卷积神经网络在钢框架数值试验数据上的训练准确率Table 5 Training accuracy of the CNNs on data from numerical test of steel frame

表6 卷积神经网络在钢框架数值试验测试集上的损伤识别概率Table 6 Damage identifying probability on test data set from numerical test of steel frame

3.3 振动台试验

为了进一步验证方法的有效性，文中在实验室中进行了悬臂梁振动台试验。试验所选用的悬臂梁材料和几何参数以及边界约束条件同第3.2.1节，损伤采用人工切割缝模拟，包括不同裂缝数量和不同裂缝深度等5个损伤工况如表7所示，其中2 mm深度裂缝相应的截面损伤程度为10%，4 mm深度的截面损伤程度为20%。试验采用电动振动台产生的随机激励模拟有限带宽白噪声振动，激励的功率谱密度取0.1（m/s2）2/Hz，激振频率带宽为5 Hz～1 000 Hz。悬臂梁从自由端到固定端布置7个加速度传感器采集悬臂梁水平加速度，测点布置如图4所示，试验装置如图7所示。悬臂梁各个测点的加速度信号采样频率为5 000 Hz，每一种损伤工况采集时长为30 s 的加速度信号，即每个测点150 000 个时刻点，从而每种损伤工况可得到一个150 000×7 的加速度信号矩阵。然后从每个序列中随机抽取1 000个大小为1 024×7的子矩阵作为样本矩阵，共得到5×1 000=5 000个样本矩阵作为卷积神经网络的输入样本，按照7∶2∶1的比例划分成训练集、验证集以及测试集。

表7 振动台试验悬臂梁损伤工况Table 7 Damage cases of the cantilever beam in shaking table test

图7 悬臂梁振动台试验装置图Fig.7 Device for shaking table test of cantilever beam

图8 给出了单尺度和多尺度卷积神经网络在实测加速度信号的训练集和验证集上的训练曲线，表8 给出了训练准确率，可以看出：单尺度卷积神经网络的准确率和损失函数收敛相对比较缓慢，而多尺度卷积神经网络均能快速收敛到理想水平，训练集和验证集的训练曲线基本一致，没有过拟合现象；单尺度卷积神经网络在本例的实测数据上也取得了较好的训练效果，准确率在90%以上；多尺度卷积神经网络的训练准确率在训练集和验证集上几乎都达到了100%。

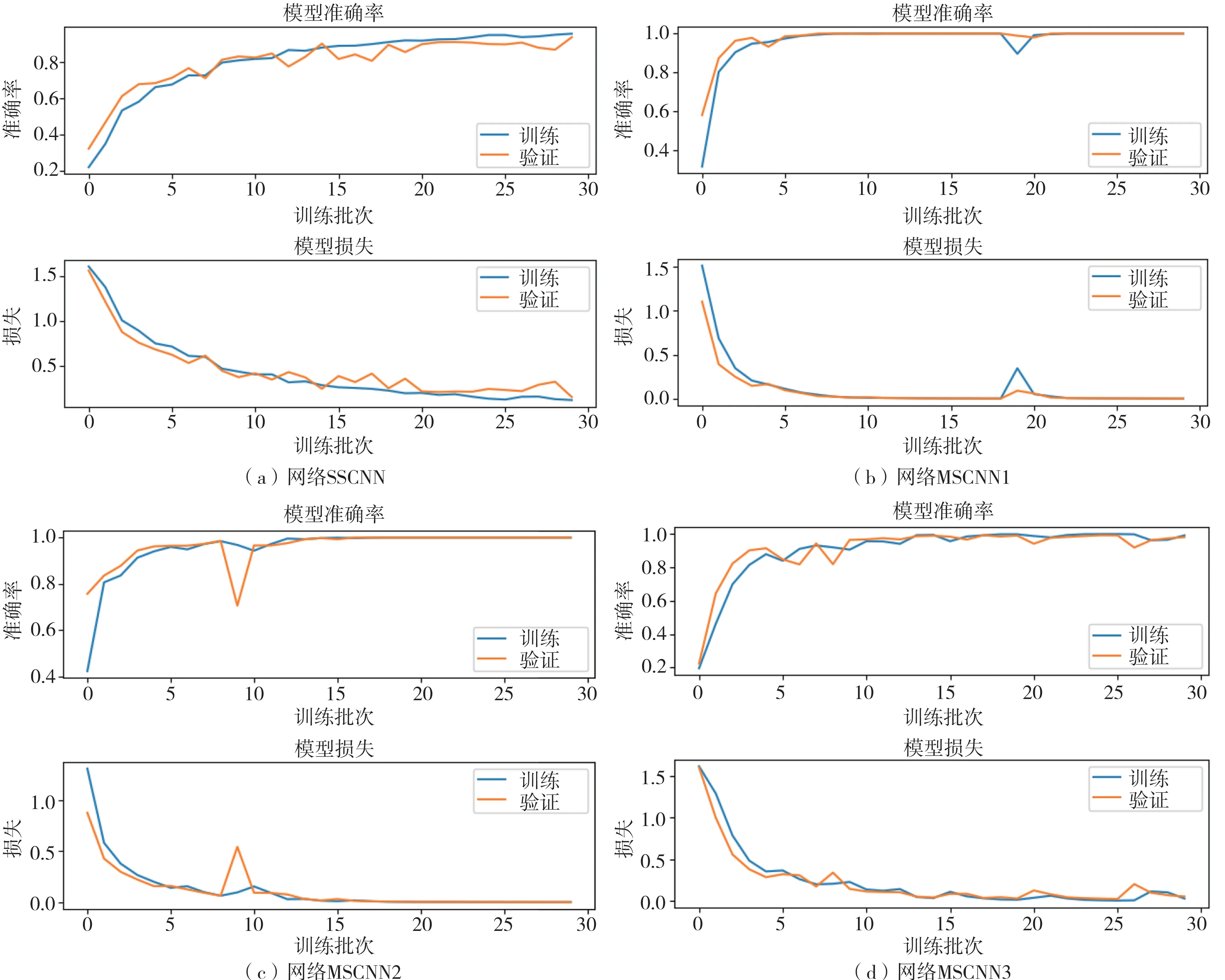
图8 卷积神经网络在振动台试验数据上的训练曲线Fig.8 Training curves of the CNNs on data from shaking table test

表9给出了训练好的各种卷积神经网络在测试集上对各个损伤工况的识别精度，可以看出：按照概率最大损伤判别法则，每种卷积神经网络都能准确识别出各个损伤工况，但是相对于其它损伤工况，工况3和工况4的识别精度要低一些，这是由于损伤工况3和工况4比较接近，只相差了一道深度为2 mm的浅裂缝。图9给出了各种卷积神经网络识别各个损伤工况的混淆矩阵，可以看出：单尺度卷积神经网络在识别损伤工况0、工况1和工况4时可以达到很高的识别精度，但是工况2和3之间存在一定程度的混淆。比如：在识别工况2时，100个样本中76个识别正确，24个被误判成损伤工况3；识别工况3时，100个样本中87个样本识别正确，13个样本误判成工况2。再次说明，由于损伤工况2和工况3之间比较相似，辨别难度较大，存在一定的误判混淆度。对于多尺度卷积神经网络，这种混淆程度大大降低，损伤工况0、工况1和工况4的识别精度达到100%，损伤工况2和3的识别精度几乎都在90%以上，较之单尺度卷积神经网络，损伤识别性能大大提升。

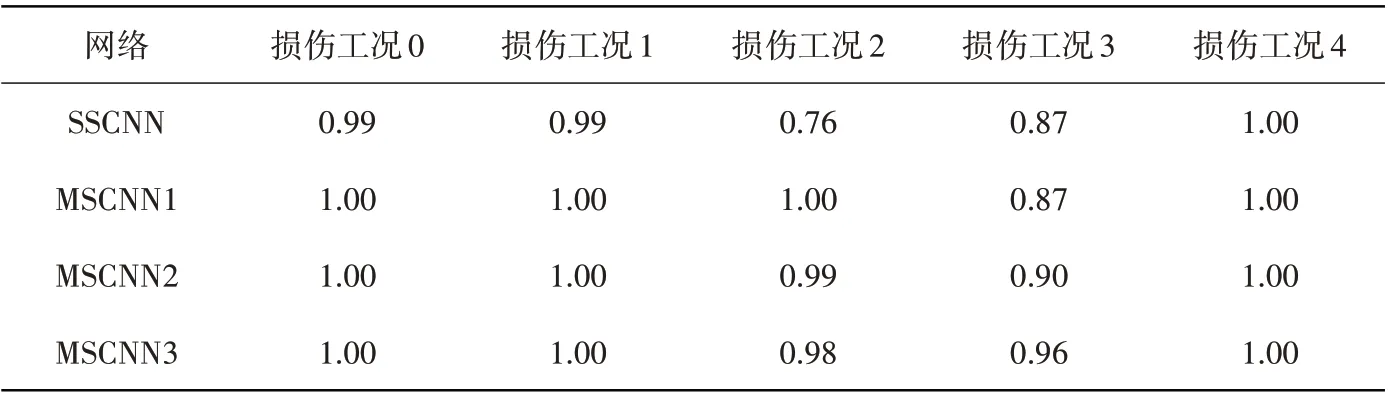
表9 卷积神经网络在振动台试验数据测试集上的损伤识别概率Table 9 Damage identifying probability on test data set from shaking table test

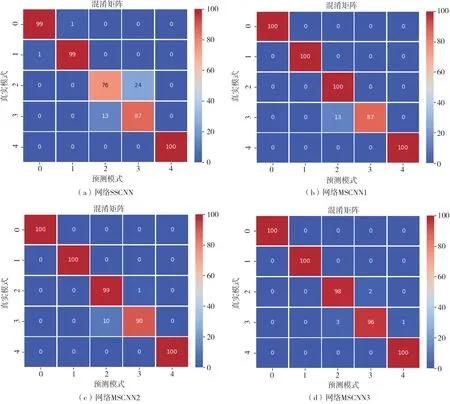
图9 振动台试验数据测试集上的损伤识别混淆矩阵Fig.9 Confusion matrix for damage identification test data set from shaking table test

4 结论

文中通过对输入的结构振动加速度信号进行下采样和滑动窗口平均处理以及在卷积运算中采用不同尺寸的卷积核，实现了两种多尺度卷积神经网络，即多尺度输入卷积神经网络和多尺度卷积核卷积神经网络；并给出了两种卷积神经网络的结构和参数取值的建议。数值试验和振动台试验表明：由于能够提取加速度信号中的多尺度特征，与单尺度卷积神经网络相比，多尺度卷积神经网络具有更高的损伤识别精度和良好的抗噪性；对于损伤特征相近的损伤模式，具有更高的辨识能力和较低的误判率。多尺度卷积神经网络虽然具有优良的损伤识别能力，但是与单尺度卷积神经网络一样存在网络结构和网络参数的优选问题，为了确定合理的网络结构和参数，需要进行大量的试验，存在一定的主观性，因此需要进一步研究网络结构和参数的自动优选问题；此外，文中仅仅对简单结构的损伤定位进行了研究，对于损伤程度判别以及复杂结构和实际工程结构的损伤识别需要做进一步研究。