基于参数化模型的架空直立式码头损伤诱因反演*

左良栋，周世良，曹诗宝，吴 俊

(1.重庆交通大学 河海学院，重庆 400074；2.重庆交通大学，重庆西南水运工程科学研究所，重庆 400016)

内河架空直立式码头的数量越来越多、应用越来越广泛。由于对架空直立式码头结构损伤机理研究认识不深刻，且无相应的结构监测措施，码头损伤破坏问题普遍存在。针对码头损伤诱因分析可分为5种类型：1)材料劣化。Wall等[1]测量并分析了钢筋混凝土构件锈蚀速度及其影响因素，Paul等[2]分析了钢筋混凝土碳化深度影响因素和演化过程。2)超载、野蛮靠泊和水流作用。范云生等[3]、Xie等[4]利用有限元方法分别对船舶撞击架空直立式码头的碰撞过程、靠泊能力、最大撞击力、码头基桩应力、位移变化进行仿真分析。3)超限堆载。李越松等[5]、Zeng等[6]指出后方堆载导致土体水平位移和承台构件相对错位，王元战等[7]研究了堆货荷载下架空直立式码头结构损伤特性。4)岸坡失稳。吴红霞等[8]、袁和平等[9]、Li等[10]得出岸坡滑动或不稳导致码头变位和损伤，施斌[11]指出架空直立式码头不均匀性沉降导致桩帽竖向开裂。5)地震。张文敬[12]、Li等[13]、Heidary等[14]建立了桩-土-结构有限元模型，分别针对码头面板及桩的位移和加速度动态响应、桩基内力变化、非结构性构件在地震作用下的响应特性等进行深入研究。

现有桩基检测方法主要有：静载荷试验法、钻孔取芯法、声波透射法、低应变检测法、高应变检测法、模态参数识别法、光纤传感检测法等。但这些技术仅能实现对桩基结构的不定期结构检测，有些还会对桩基造成损伤。

本文拟通过综合利用力学分析、有限元计算、信息融合等方法，建立码头桩基受力特性与损伤诱因之间的内在关联机制与反演模型，对主要损伤诱因的相关参数进行反演，并对反演结果和模型性能进行分析，使桩基由传统的承力结构上升为具有自感知能力与“窗口”作用的智能结构，实现内河架空直立式码头不良诱因反演功能。

1 参数化有限元模型

神经网络模型具有非常强大的泛化能力和非线性映射能力，模型的输入对模型预测结果优劣发挥至关重要的作用，当输入的样本数量少时会造成模型欠拟合，模型对于给定的数据集能够得到较好的预测，但对于新数据集预测较差，显然不利于损伤诱因的识别，为了得到良好的预测结果，需要采集大量的数据样本。对于实体单元模型而言，其单元数量多、本构关系复杂、边界条件复杂，软件计算存储开销大、计算时间长，不利于大数据大样本的获取。故通过Python的subprocess库调用有限元计算程序的方式进行参数化模型的计算和数据的提取。

1.1 建模方式简化

采用ANSYS Parametric Design Language和铁木辛柯梁理论进行参数化建模。对于码头结构桩基、纵梁、横梁、立柱等构件采用beam188单元，其余码头面板采用shell181，将基岩层和抛填层考虑成弹性体，采用combin14弹簧单元。钢筋混凝土与钢结构材料均采用线弹性模型，与实体单元模型相同。见图1。

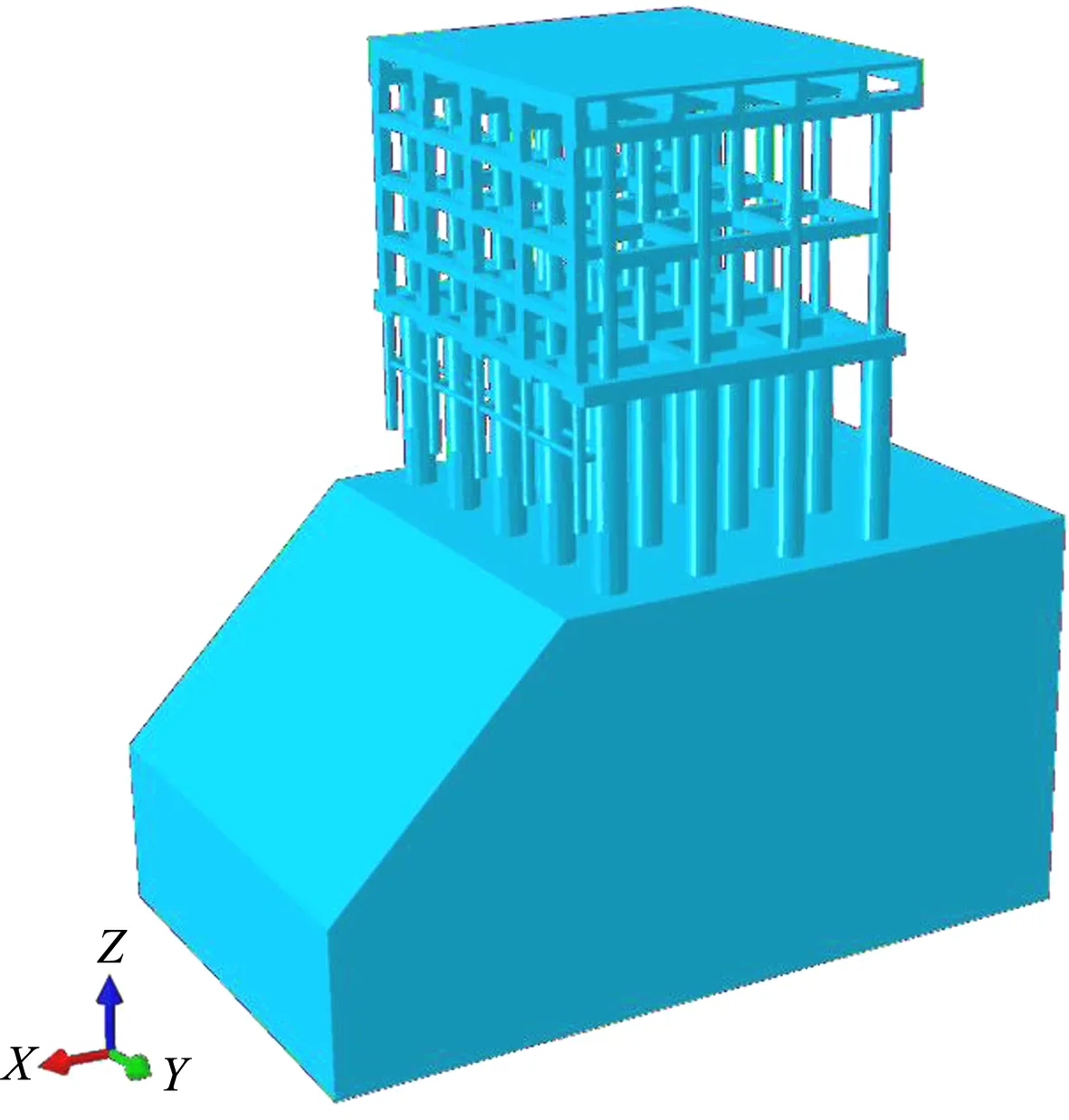
图1 架空直立式码头实体模型

1.2 边界条件简化

假定岸坡作用为水平推力，则桩基在岸坡作用下为水平受荷桩，因此可以考虑采用弹性地基梁法模拟简化模型的桩土约束。将抛石层和基岩层假定为弹性体，将桩视为弹性地基上的梁。嵌岩和抛填部分采用土弹簧combin14进行模拟，在水平面上做双向弹簧约束，桩基底端采用固结形式。

1.3 加载方式

选取船舶靠泊、岸坡滑动、不均匀堆载这3种高桩码头的代表荷载，在load分析步中分别施加，各种荷载的加载方式如下：船舶吨位按照6 000 t，靠泊速度取值为20 cm/s，计算得到靠泊力大小取值为420 kN，作用点分别取X方向160、165、170 m 共3个位置。

按照GB 50007—2011《建筑地基基础设计规范》附录Q的相关规定，当桩基上部横梁最大位移为0.04 m时，抛填块石层后方岸坡推力为2 MPa的稳定荷载，施加位置为岸坡后方X方向。不均匀堆货荷载采用码头前方堆货荷载作用的大小取20 kPa，为距前沿10 m范围内；后方取30 kPa，为距后沿20 m范围内均布，作用方向为-Z。

1.4 损伤诱因参数化

根据JTS 144-1—2010《港口工程荷载规范》及GB 50007—2011《建筑地基基础设计规范》的有关规定，结合三峡库区架空直立式码头受力特点，将损伤诱因确定为3个：码头不均匀堆载、船舶靠泊和岸坡推力。作用范围见图2和表1，各损伤诱因的参数化指标见表1。

图2 损伤诱因作用点分布(单位：m)

表1 损伤诱因参数量化

1.5 参数化模型验证

为验证参数化模型的准确性，与实体单元模型做对比，将相同位置、相同大小的荷载同时施加在两个模型上进行计算。对比中间排架4根桩顶竖向位移和应力。

由表2的计算结果可得，桩顶竖向位移值平均相差14.5%，简化模型平均竖向位移比实体单元模型要大。因为实体单元模型下部是基岩和抛填层，对桩基起到了嵌固作用，减少了桩顶的竖向位移。

表2 桩顶竖向位移计算结果 mm

表3为桩顶竖向应力值对比，平均相差5.3%。简化模型和实体单元模型桩顶竖向应力整体相差较小。

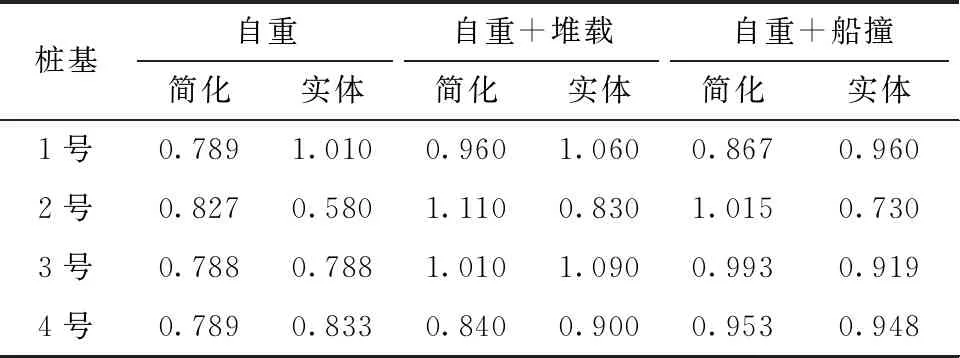
表3 桩顶竖向应力计算结果对比 MPa

由以上对比分析，参数化简化模型与实体模型计算结果差异不大，可以作为反演分析的模型使用。将简化有限元模型设置为调用模型，随机抽取量化的不良作用参数，将参数载入求解文件(求解文件是ANSYS命令流文件，包含调用有限元模型的命令，所有的荷载的命令，后处理提取应力的命令，以及导出数据的宏文件)，Python的子程序库subprocess进入MANSYS模块，导入求解文件，让其自行调取有限元模型进行计算采集数据并导出。

2 单一损伤诱因效用反演

为了测试神经网络模型对于复杂应力特征的适应性，本节主要采用抽样的方式抽取单一诱因的样本工况，将其投入简化模型进行计算，提取批量的应力特征数据。

2.1 堆载作用反演分析

参数优化采用Python的机器学习库sklearn中的网格搜索算法Gridsearch，对神经网络的隐含层，惩罚因子进行搜索，利用交叉验证精度来验证参数优化后的神经网络模型的性能。经过网格搜索得到神经网络反演模型优化参数，见表4。

表4 神经网络模型最优参数

2.1.1位置识别

位置识别属于分类问题，分类学习器采用交叉熵损失作为模型损失指标，由图3可知，当神经网络模型迭代117次时，模型收敛。

图3 堆载作用下分类学习器损失曲线

为检验模型对堆载诱因各个作用位置处的泛化能力，将训练集和测试集按位置进行统计，并通过训练好的模型分别对训练集和测试集进行评分，得到具体指标见表5。

表5 位置识别结果

由表5可见，对于训练集4个区域的位置识别精度达到0.989，测试样本的识别精度也达到0.978，精度表示模型对位置识别的准确性，最优值为1；F1表示对样本召回数量和准确率的调和平均数，最优值为1；汉明损失表示模型计算值与真实值之间的差值，最优值为0。F1指标和汉明损失指标均比较理想，并且训练集和测试集的指标和评分相差较小，说明神经网络模型性能调校较好、泛化能力较强、能够正确识别堆载诱因的位置。

2.1.2大小识别

大小识别属于回归问题，回归学习器采用方差作为模型损失指标，由图4可知，当神经网络模型迭代225次时，损失误差达到0.001左右，此时即可判定模型收敛。

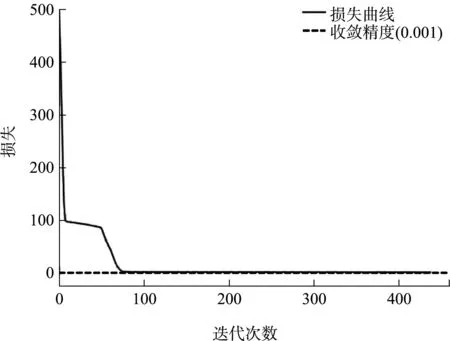
图4 堆载作用下回归学习器损失曲线

将训练集和测试集按位置进行统计，得到模型的结果，见表6。

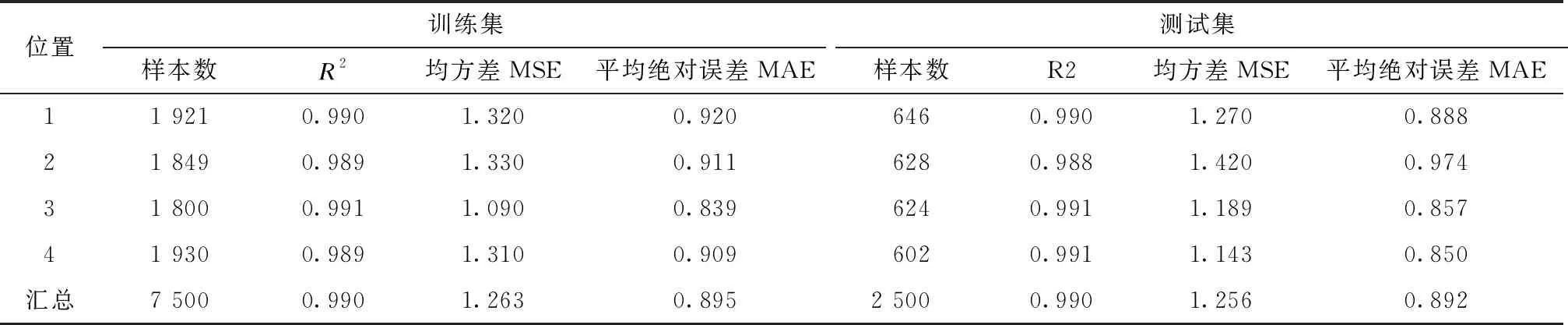
表6 大小识别结果

由表6可以知，训练集和测试集拟合优度指标R2最小值达到了0.98，对于回归模型而言，拟合优度指标不能完全判断预测值的精度，还要看均方差和平均绝对误差，表中均方差和平均绝对误差结果相对较低，为比较平均绝对误差相对于堆载作用的取值的大小，绘制了测试集绝对误差图和相对误差图，并随机抽取了预测样本中的20个样本进行预测值和真实值对比，见图5。

图5 大小识别结果曲线

由图5可见，绝对误差均小于4.0 kPa，平均绝对误差在0.892 kPa左右，平均相对误差为2.97%，对堆载诱因大小识别，模型表现比较优秀。对堆载诱因作用1万个样本，训练集和测试集的指标和评分相差较小，说明构造的神经网络反演模型预测能力较好，不存在拟合能力欠缺和多度的情况；泛化能力较强，能够对堆载作用的位置、大小进行准确高效的预测，满足一般条件下损伤诱因的判别要求。

2.2 船舶靠泊和岸坡推力作用反演分析

限于篇幅，以2.1中的分析方法，开展船舶靠泊和岸坡推力损伤诱因的详细过程不再表述。经分析，文中使用的方法对两种损伤诱因均能取得良好的反演效果。

3 混合损伤诱因效用反演

在相同类型的不良作用下，码头应力特征具有相似性，将具有相似性特征的样本输入模型，必然会导致模型识别精度的提升，而神经网络反演模型对样本数据特征非常敏感，将三类损伤诱因作用的数据集整合成一个数据集作为反演模型的输入，观察一个反演模型对损伤诱因的类型、位置和大小的适应性和识别精度。分析结果见表7。

表7 混合损伤诱因识别结果

由表7可见，模型可非常准确地判断所有样本分属损伤诱因作用的类型，说明不同损伤诱因类型下的桩基应力分布具有清晰的边界，模型可根据样本特征进行准确识别；堆载作用下样本位置识别精度达到0.980，船撞作用位置识别精度达到0.900，相较于单一船撞样本精度有所下降，但仍具有较好的识别效果；岸坡作用仅有一个作用位置，不必识别；堆载作用下样本位置识别精度达到0.965，相较于单一船撞样本精度有所下降，船撞作用位置识别精度达到0.990。

总体而言，反演模型对混合样本整体表现较好。相较于单一作用类型的样本，对堆载作用，位置识别精度基本不变，大小识别精度有所降低；对于船撞作用，位置识别精度降低了5%作用，大小识别的精度保持不变；对于岸坡作用，精度不变。

4 结论

1)通过Python的subprocess模块调用MANSYS模块进行分析，证明了批量计算的可行性，并通过与实体单元模型进行应力特征对比，分析知两种模型差别不大，简化模型数据可以进行替代计算。

2)通过网格搜索的方式搜索神经网络模型的最优参数，交叉验证得到模型评估指标的得分，并分别对堆载作用、船撞靠泊和岸坡推力损伤诱因进行分析。经分析，堆载作用位置识别精度为0.980，大小识别的平均绝对误差在0.892 MPa；船撞作用位置识别精度为0.940，大小识别的平均绝对误差在5.5 kN；堆载作用位置大小识别的平均绝对误差在1.2 kN；反演模型对单一损伤诱因样本具有非常好的泛化能力。

3)将所有样本整合，进行混合损伤诱因分析并检测神经网络反演模型的性能，分析得知混合样本集反演结果，类型识别精度在1.00，位置识别精度0.940，大小识别平均绝对误差为2.2；模型在个别损伤诱因识别指标上出现了精度和评分的下降，但其总体预测精度仍满足了反演识别的一般要求。

4)本文施加的外部荷载为竖向和横向，未考虑纵向水流力和系缆力的作用的影响，纵向荷载的作用必然会对模型识别精度造成一定影响，但考虑到码头结构纵向刚度较大，加之纵向荷载对结构物整体安全性的影响不是主导因素，为此本文未作单独讨论。

5)实际工程中，岸坡沉降和结构变形等数据均为长期累积结果，本文计算中未考虑长期作用效应，这对反演结果的真实性有一定影响，实际应用中可将沉降和变形稳定后的数据作为反演样本。