局部损失系数数值仿真研究*

沈方荣 ，何正为 ，侯英岢 ，章勇杰 ，黄政晖 ，杨维鑫

（浙江农林大学光机电工程学院，浙江 杭州 311300）

0 引言

弯管局部损失系数应用的领域极其广泛，例如冷板作为液冷散热系统重要的组成部分[1]，其内部流道复杂多变，压力损失是影响冷板性能的指标之一，而局部损失系数是管道内压力损失的重要系数，但不同弯管的局部损失系数差别很大[2]。

Zhang Hao等[3]研究了局部阻力系数随雷诺数、直径比和壁面粗糙度的变化规律。研究表明，流体的局部阻力系数随雷诺数变化不大，壁面粗糙度对局部阻力系数有显著影响。邵敬宇等[4]对直角弯管进行了数值模拟，探求雷诺数和相对曲率半径对直角弯管局部损失系数的影响。杨少东等[5]针对大管径通风弯管，对450 mm、750 mm、1 000 mm、1 500 mm、2 000 mm和不同曲率半径比的90°进行数值模拟，获得其局部损失系数，研究了流体流动特性并分析了弯管局部损失产生的主要原因。杨任等[6]用fluent对弯管进行数值模拟，研究表明，沿程阻力系数和局部损失系数都与雷诺数有关并随着雷诺数的减小而增加。陈晓等[7]针对90°弯管的 Z 形组合进行数值模拟研究，研究表明，弯管间会产生不同程度的局部损失相邻影响。秦明坤等[8]针对90°弯曲管道内湍流流动进行数值模拟，研究表明，二次流强度随r/d减小和Re数的增大而增加。

课题组研究方管管径、曲率半径比和弯管角度对局部损失系数的影响规律，获取弯管压力损失系数计算公式；对冷板模型进行理论计算和数值模拟，将理论计算结果与数值模拟结果对比，验证计算公式准确性。

1 弯管局部损失系数的数值仿真

1.1 弯管几何模型的建立

目前，局部损失系数没有具体统一计算方法和数值[9]，本研究以常见的90°和180°弯管为研究对象，研究方管直径、曲率半径比对局部损失系数的影响规律，将方管管径d设置为6种（5 mm、10 mm、15 mm、20 mm、25 mm、30 mm），曲率半径比r/d设置14种（0.6、0.8、1.0、1.2、1.4、1.6、1.8、2.0、2.5、3.0、3.5、4.0、4.5、5.0）。图1为一个单直角弯管；图2采用两个串联弯道，为了减少串联型流道中相邻180°弯管对局部损失系数产生的影响。取入口段管长为20d。

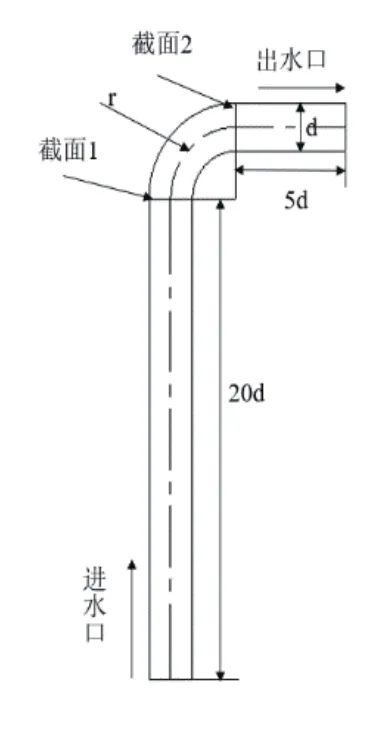
图1 90°弯管

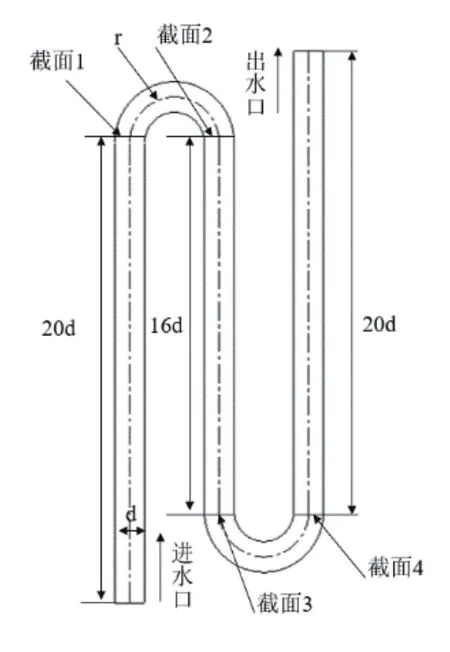
图2 180°弯管

1.2 数值仿真结果及分析

第一步，导入弯管几何模型；第二步，设置边界条件及材料，进口流速1.415 m/s，流体是水，流动状态为湍流；第三步，划分网格；第四步，设置迭代步数。数值模拟获得图1与图2中截面中心点的压强，两个截面的中心点的压差即为弯管压力损失ΔP。采用以下计算公式获取局部损失系数ζ：

式中，ΔP——弯管压力损失；ρ——流体密度；v——流体流速。

图3、图4为90°和180°弯管的局部损失系数，随不同曲率半径比和方管管径的变化规律。在相同管径下，局部损失系数随着曲率半径比的增大呈现先减小后增大的趋势。曲率半径比r/d≈1.6，90°弯管局部损失系数最小；曲率半径比r/d≈1.7，180°弯管局部损失系数最小。原因是曲率半径比越小，流体在弯管处受到的惯性力和离心力的作用就越明显，产生二次流，从而导致局部损失系数就越大。但随着曲率半径比的增大，流体在弯管处的二次流减弱。而曲率半径比相同的情况下，局部损失系数随着管径的增大而减小，且管径越大局部损失系数减小的趋势越缓。原因是管径越小，流体在弯管处扰动越剧烈，压力损失越大，局部损失系数也就越大，而管径越大，水在弯管处的紊乱程度越平稳，压力损失就越小，局部损失系数也就越小。

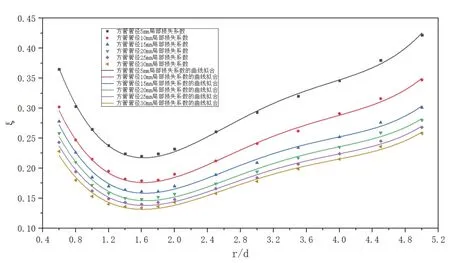
图3 90°弯管局部损失系数的变化规律

图4 180°弯管局部损失系数的变化规律

表1和表2为拟合得到的局部损失系数计算公式。可应用于机械、土建、石油、化工、水利、液压传动等各个领域，解决管路中压力损失计算的问题[10]。

表1 90°弯管局部损失系数计算公式

表2 180°弯管局部损失系数计算公式

2 弯管局部损失系数计算公式验证

2.1 冷板几何模型建立

如图5所示，为冷板内部流道结构示意图。已知环境温度20 ℃，冷板材料为6061铝合金，尺寸为300*300*20 mm，流道截面积为15×15 mm；冷却液为水，温度20 ℃，流速为2 m/s。

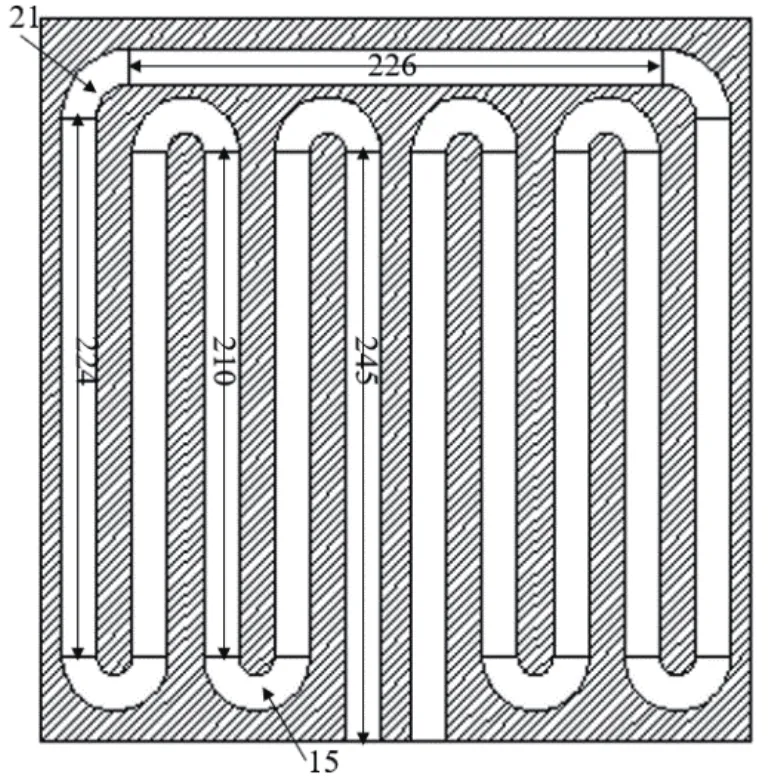
图5 冷板内部流道示意图

2.2 数值模拟

首先，将冷板模型导入Icepak；其次，设置各部件材料属性、基本参数与边界条件，选用Zero equation湍流模式，网格设置为Mesher-HD，网格最大尺寸x、y、z设置为0.6、0.3、0.6；最后，设置求解步骤为100步。如图6所示，冷板进出口压力损失为16 422 Pa。

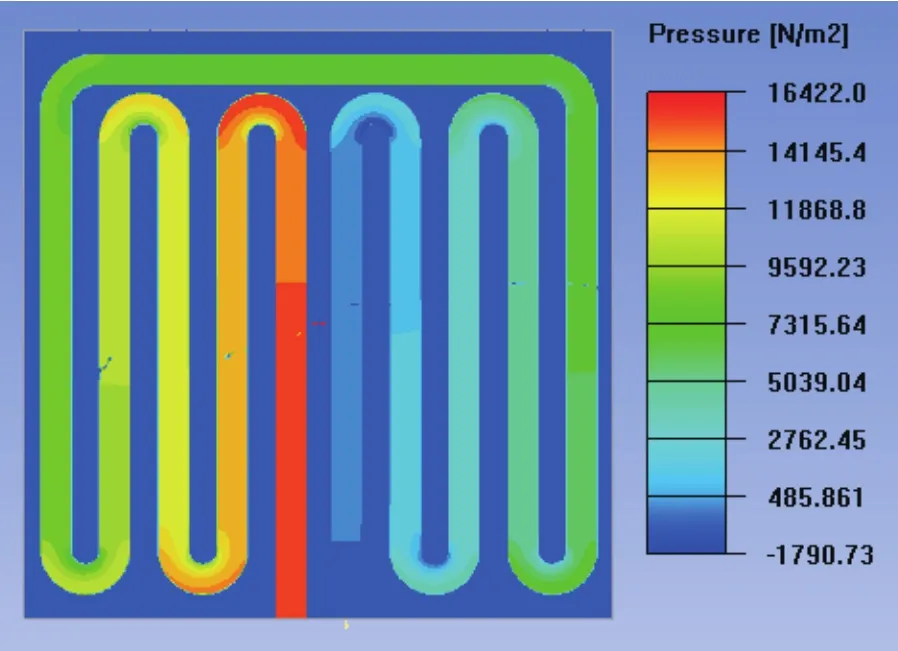
图6 进出水口压力

2.3 压力损失的理论计算

流道中总的损失包括沿程损失与局部损失。沿程损失：在流道的直道段上单位重量的流体因与管壁发生摩擦以及流体之间的内摩擦而造成能量损失。局部损失：流体在流道的某些局部地方，由于管径的改变以及方向的改变，或者由于安装了某些配件而产生额外的能量损失。

雷诺数Re是一种可用来表征流体流动情况的无量纲数。利用雷诺数可区分流体的流动是层流还是湍流，也可用来确定物体在流体中流动所受到的阻力。

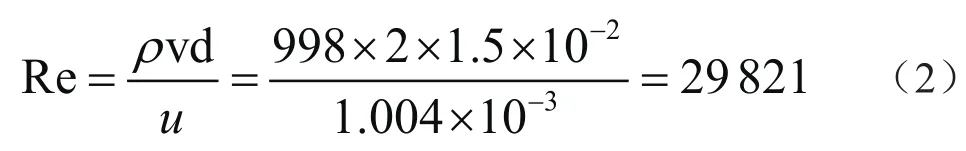
式中：d——当量直径；u——水的动力黏度。

Re＜2 300为层流状态，Re=2 300~4 000为过渡状态，Re＞4 000为湍流状态。可见本研究中流体在流道内的状态为湍流。

沿程损失系数f，采用布拉修斯公式：

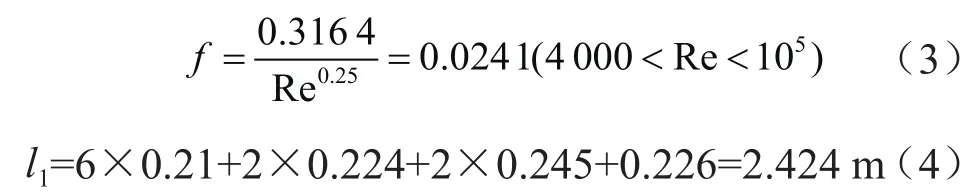
式中：l1——流道直道长度。

沿程损失hf的计算，通常采用达西公式：

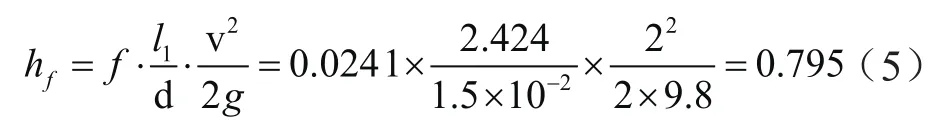
该冷板结构由8个180°且曲率半径比为1的弯管和2个90°且曲率半径比为1.4的弯管组成。利用表1、表2中的计算公式可求得局部损失系数ζ1、ζ2分别为0.162和0.456。

流道中总的局部损失系数ζ：

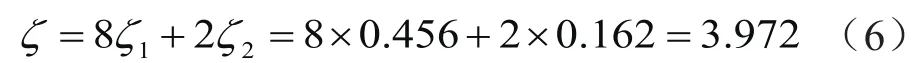
关于局部损失hj，采用以下计算公式：

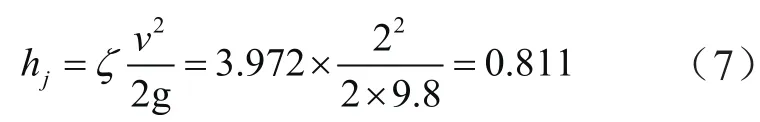
冷板的压力损失ΔP：

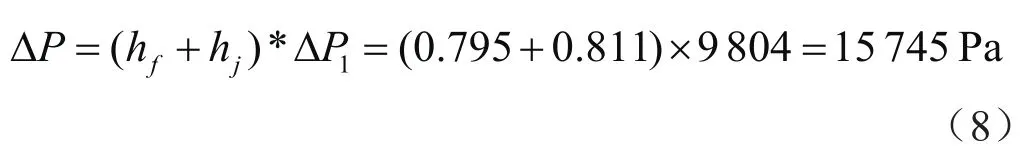
2.4 理论值与模拟值对比验证

表3为压力损失的理论值与模拟值，分别为15 745 Pa和16 422 Pa，比较计算结果与仿真结果误差值，验证了计算公式的准确性。

表3 压力损失理论值与模拟值

3 结论

本研究以90°和180°弯管为研究对象，得出以下结论：在管径相同的情况下，随着曲率半径比r/d的增大，局部损失系数先减小后增大。曲率半径比r/d≈1.6，90°弯管局部损失系数最小；曲率半径比r/d≈1.7，180°弯管局部损失系数最小。在曲率半径比相同的情况下，局部损失系数随着管径的增大而减小。通过理论计算与仿真结果对比，理论计算与数值模拟的压力损失分别为15 745 Pa 、16 422 Pa，误差为4.29%，其误差在合理范围内，验证了计算公式的准确性。