一种鲁棒的分布式雷达主瓣干扰抑制方法

蒲伟铭 梁振楠 陈新亮 吴建新 刘泉华

（1.北京理工大学信息与电子学院雷达技术研究所，北京 100081；2.中山大学电子与通信工程学院，广东广州 510275；3.北京理工大学重庆创新中心，重庆 401135）

1 引言

现代战争中的电磁环境日益复杂，电磁干扰成为雷达对抗中的关键问题［1］，当干扰信号从天线主瓣进入而形成主瓣干扰时，受到天线的高增益调制，能够造成严重的干扰效果［2］。目前抗主瓣干扰技术主要从时域、空域、极化域展开：

（1）频率捷变技术［3］，雷达通过不断调频使干扰机跟不上雷达的频率切换速度以达到抗干扰的目的，但面对瞬时复制雷达信号并转发的数字射频存储转发式（DRFM）干扰时该方法失效；

（2）自适应变极化干扰抑制技术［4］，通过检测干扰信号的极化方向，改变雷达发射信号的极化方式与其正交以实现对干扰的抑制，但实际场景中可能部署多部极化方式不同的干扰机导致该方法失效；

（3）传统的空域自适应处理方法［5］应用于主瓣干扰抑制时会造成主瓣偏移和主波束变形等问题。

综上所述，单基地雷达的各种抗干扰手段均不能有效抑制主瓣干扰。分布式雷达［6-7］由一部主雷达和多部辅助雷达按照特定位置进行部署并协同工作以形成等效大孔径阵列，借助全阵列极高的角度分辨率对消主雷达的主瓣干扰［8-9］。

在实际应用中，各单元雷达相对位置难以准确标定、各雷达信号传输到处理机的时延不同，这类非理想因素最终会造成通道间的幅相误差，严重影响分布式雷达系统的抗干扰性能。分布式雷达系统依靠空域滤波对干扰进行抑制，常用的准则有MVDR 准则［10］和LCMV 准则［11］等，当通道间存在幅相误差时，准则中所用的导向矢量与实际的导向矢量不一致，造成信噪比损失；最具有代表性的稳健波束形成算法是对角加载算法［12］，但其性能严重依赖于对角加载因子的选取，而在复杂的干扰场景下，对角加载因子的选取变得十分困难。

因此，分布式雷达需要在抑制干扰前校正系统的幅相误差。传统的幅相误差校正方法分为有源校正和自校正，有源校正是指在信源个数和方向已知的情况下对误差进行估计［13-14］，但分布式雷达由于基线较长，部署后进行有源校正比较困难；自校正是指在信源已知信息较少或完全未知的情况下对误差进行估计［15-16］。由于信源角度信息与相位误差耦合，自校正需要对角度和相位误差进行联合估计，难度较大。已有的幅相误差自校正算法一般对阵列有一些要求［17-18］，文献［17-18］要求阵列为部分校正阵列，即部分阵元已经被精确校正，不存在幅相误差，依赖这部分阵元对剩余的存在幅相误差的阵元进行校正；文献［15］则是要求阵列构型为均匀线阵。

为了在非理想条件下实现主瓣干扰对消，本文提出一种在干扰对抗阶段先通过广义内积法提取出单一干扰信号，利用干扰信号进行角度-幅相误差的先后估计，再采用MVDR 波束形成器进行主瓣干扰抑制的方法。并证明该方法虽然存在相位误差残余的问题，但能使主瓣内信源的相位维持与阵元位置的线性关系，提升了干扰抑制后的输出信噪比。

本文第1节简述了分布式雷达的研究背景与现状，简述了本文主要内容；第2节介绍了分布式雷达系统存在幅相误差时的信号模型；第3 节介绍了样本选取和幅相误差估计的算法原理，并对幅相误差补偿后的误差残余的影响进行了分析；第4 节通过仿真验证了本文方法的有效性；第5 节对本文进行了总结。

2 信号模型与问题描述

2.1 系统描述

分布式雷达系统由一个主雷达和N个辅助雷达组成，如图1 所示。X0为主雷达，X1～XN为辅助雷达。由于伴飞干扰机离目标距离较近，当主雷达单独工作时，干扰机全部位于主雷达的主瓣以内（如图1实线所示）；但当多个辅助雷达与主雷达协同工作时，由于阵列基线变长，全阵列的合成主瓣变窄（如图1虚线所示）。

2.2 信号建模

设主雷达接收到一远场窄带信号s0(t)，波达方向与主雷达法线夹角为θ0。则一维分布式雷达系统全阵列的接收数据可表示为：

式中a为该信号的导向矢量，a=，λ为信号波长，di为第i个雷达相对于相位中心（一般设主雷达为相位中心）的距离，N(t)为高斯白噪声。

各雷达的位置误差和传输时延等非理想因素会给分布式雷达系统引入随机的幅度和相位误差，则接收数据为：

式中Λ为幅度误差矩阵，Λ=diag(η0，η1，η2，…，ηN)，ηi为第i个通道的相对于参考通道的幅度误差，Γ为相位误差矩阵，Γ=为第i个通道的相对于参考通道的相位误差。

引入幅相误差后导致导向矢量a发生变化：

从式中可以看出相位误差与信号的角度信息耦合，给后续的信号处理造成了极大的困难。

3 基于干扰样本的幅相误差补偿方法

本文提出的方法先通过干扰样本选取算法提取出压制干扰数据段，再使用所提取出来的数据段进行幅相误差的估计，最终用补偿后的数据进行MVDR准则下的主瓣干扰抑制。

3.1 基于广义内积的干扰样本选取

广义内积算法是一种常见的非均匀样本检测算法（NHD）［19］，其计算公式如下：

式中M为采样点总数，RY′为数据样本Y′的协方差矩阵。

从上式可以看出广义内积是数据白化矢量的内积，可以从白化矢量的能量角度检测数据的均匀性：对于统计意义上均匀的数据（噪声式干扰等），RY′可将其白化，得到的GIP 值等于其数据维度；而对于统计意义上非均匀的数据（欺骗式干扰等），RY′则无法将其白化，其GIP 值则要远远大于其数据维度，以数据维度值为门限，即可将数据中存在欺骗干扰的数据段剔除，得到仅有压制干扰的数据段。由于噪声和其他非理想因素影响，门限值可能需要根据实际情况进行调整。

此外，由于Y′中可能含有非均匀数据，导致剔除效果不佳，为了能够有效剔除非均匀数据点，需要进行迭代处理。比如在第一次样本选取中仅挑选出了部分非均匀数据，则将该部分数据从Y′中移除重新计算协方差矩阵RY′再进行一次样本选取，设置迭代次数上限或剔除点数上限中止迭代，以达到更好的剔除效果。

3.2 基于牛顿迭代法的幅相误差补偿

仅有压制干扰的数据段形式如下：

式中aj为该压制干扰的导向矢量，aj=，θj为压制干扰的波达角。

对每个通道做自相关即可得到幅度补偿矩阵，即协方差矩阵的对角线元素的逆矩阵：

进行幅度补偿后仅剩相位误差：

由于相位误差与角度信息耦合，需预先对信源进行角度估计，对回波数据进行方位角度范围C的常规波束形成：

yθ(t)为θ角度的波束数据，通过求和的方式对该干扰在各个波束下的增益进行估计：

根据响应图峰值估计强干扰所在角度，得到对应角度导向矢量a(θj′)。

数据估计的协方差矩阵为：

忽略噪声影响，则：

则：R=A◦(ββH)，式中◦为Hadamard 积，β=，此时先假设对角度的估计准确，即R，A均为已知矩阵。

设定φ为取一个复数的相位角的函数，则φ(ejφ)=φ。

只取ββH的相位角构成矩阵得到：

取B的第一行，忽略0项，组成如下矩阵：

每一行都能转换成如上式矩阵，则问题转换为一个用N(N-1)个方程解N个未知数的方程组求解问题。

根据上述优化问题，可得到目标优化函数为：

式中Ψ为去相位折叠函数，形式如下：

作用是将相位角限制在-π到π之间。

牛顿迭代法实现过程如下：

式中γ(k)为待解未知数向量组第k次迭代后得到的值，α为一定步进范围内使代价函数最小的γ(k+1)值所对应的α，即：

迭代收敛后得到γ(k+1)的对角逆矩阵即为相位补偿因子。

传统的相位误差估计算法仅通过互相关估计各通道与参考通道的相位关系［20］，而本文的相位误差估计算法利用协方差矩阵应用了所有通道之间的相位关系，相当于增加了对相位关系的估计次数，减少了噪声影响，在信源的信噪比偏低的情况下能得到更高的估计精度。

仿真测试在单个阵元压制干扰干噪比10 dB 的情况下，本文所提方法相对于互相关估计相位的方法平均绝对误差下降0.2°，如图2所示。

3.3 角度估计误差带来的影响

存在相位误差时，测角结果会出现明显的偏差，而算法在相位补偿的过程中应用了存在偏差的估计角度，本小节分析了该误差会带来何种影响。

若测角结果为θj′，以该结果为参照补偿相位误差，则理论上得到的相位补偿因子μ应满足：

即补偿后该补偿源信号（提取出的压制干扰）的导向矢量与估计角度θj′方向的导向矢量一致，原真实角度θj方向导向矢量为：

则μ的理论值应为：

对于另一角度的信号：

采用求得的相位补偿因子对该信号进行补偿：

根据正弦函数的特点，当式中角度值接近0°的情况下可近似为：

则可以得到结论：补偿阶段以存在误差的角度作为标准进行校准后，对于法线附近的信源而言整体偏移相同的误差角度，即各角度相位仍保持线性关系。

3.4 幅相误差补偿后的干扰抑制

干扰抑制采用MVDR准则下的最优权矢量：

式中a(θt)为目标方向的导向矢量，Ry=E[]，为完成幅相误差补偿后的数据。

通常无法预知目标所在具体角度，只能在主瓣范围内进行搜索。当存在随机相位误差时，目标的导向矢量明显不与阵列坐标为线性关系，即在任意角度都无法对目标实现全相参；而如上一小节推导所示，在进行幅相误差补偿后，主瓣内信源都与阵列坐标保持线性关系，干扰抑制后将在目标真实角度附近得到最大输出信噪比。

4 仿真验证

本文所用的经过稀疏阵列构型设计的一维分布式雷达系统坐标如图3所示。

具体系统参数如表1所示。

表1 分布式雷达系统参数Tab.1 The Parameters of Distributed Radar System

各雷达具体位置如表2所示。

表2 雷达位置Tab.2 The Location of the radars

场景中的信源参数如表3所示。

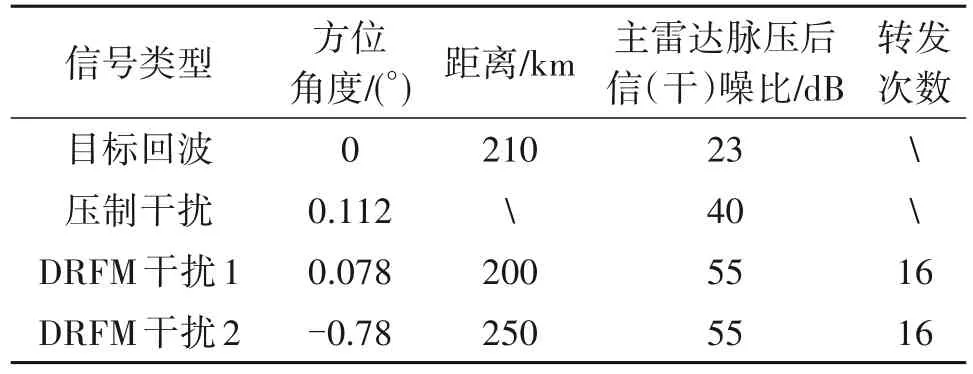
表3 信源参数Tab.3 The Parameters of the source

DRFM 干扰单次转发的脉宽为信号脉宽的1/20，转发间隔为信号脉宽的1/40。

每个阵元添加了[-45°，+45°]间均匀分布的相位误差和[-20%，+20%]间均匀分布的幅度误差。本文模型基于信源满足远场条件的情况，即信号到达各阵元时间一致。

主雷达脉压后回波如图4所示。

首先进行基于广义内积的样本选取：

本文所用样本选取算法进行了3 次迭代，为更好地剔除非均匀样本，迭代门限选取为2 倍的数据维度值，每次迭代将过门限非均匀样本剔除后再进行以此样本筛选，经仿真测试，每次迭代约比上一次迭代多剔除400 个点，证明迭代的确提升了剔除的效果。根据图5样本选取算法的结果可以从场景中提取出仅有压制干扰的距离段（小于门限的点）以进行下一步幅相误差的补偿。

由于当前相位误差添加的范围较小，所以测角误差尚不明显，压制干扰角度估计结果为0.114°，与真值仅相差0.002°。

相位误差的估计结果如图6所示。

可以观察到相位误差的估计值与真值的趋势几乎一致，虽然存在误差残余，但通过之前的推导可知相位误差残余是线性的。

遍历主瓣范围内的所有角度进行MVDR 准则的干扰抑制，统计输出信噪比，对比与传统MVDR方法的输出信噪比差异：

可以观察到传统MVDR 方法的输出信噪比在任意角度上相对本文方法的结果都会有损失，特别是在目标真实位置0°附近损失2 dB以上。

将相位误差提升至[-90°，+90°]间均匀分布，此时角度估计误差变大，误差达到0.014°，相位误差的估计结果如图8所示。

可以观察到相位误差的估计值与真值的趋势仍然保持一致，虽然角度估计误差变大导致了误差残余更多，但误差残余仍然是保持线性的。

观察各角度下的输出信噪比：

从图9 可以看出，相位误差增大后本文所提方法的优势更大，在目标真实位置附近的输出信噪比相比于传统MVDR 方法提升了约5 dB。进一步证明了本文算法的有效性。

5 结论

在大口径分布式雷达系统的应用中，幅相误差已经成为了一个亟待解决的问题。虽然在实际的工程实践中可以通过一些预标校的方式来尽量减少分布式雷达系统中的幅相误差，但如果在实战场景中部署可能并不具备理想的标校条件，本文提出了一种利用干扰样本聚焦以减少幅相误差影响的分布式雷达主瓣干扰抑制方法，提升了分布式雷达在存在幅相误差情况下的主瓣干扰抑制性能。