基于图像灰度曲线特征值的机织物密度测量
胡立文,柯 薇,梁艺馨,周 虎,邓中民
(武汉纺织大学 纺织科学与工程学院,湖北 武汉 430200)
目前,大多数工厂在机织物的密度检测上,主要还停留在人工检测阶段。大量繁杂的工作不仅容易让人产生疲劳,同时也存在很大的主观性。有部分学者利用图像处理技术来识别计算织物密度并取得了一定的成果,但仍存在测量结果不稳定的弊端。图像处理检测织物密度主要分为频率域法和空间域法2种方法。频率域法利用傅里叶变换[1-2]或小波变换[3-4],将织物转换到频域中,利用表示经纬纱线排列的峰值点或沿经纬纱线方向将织物图像分解并重构,提取纱线排列信息实现其密度的测量。空间域法根据图像亮度值可以反映织物表面纹理变化的原理,直接在空间域内利用灰度共生矩阵[5]或自相关函数计算并提取灰度特征值,即求取曲线周期或统计灰度曲线波峰个数从而得到经纬纱线根数[6-8]。
空间域法中,由于杂质信号的存在,会在波峰周围出现许多较小的杂质波峰,难以准确统计波峰个数。对此,传统上通常会利用滤波的方法对曲线平滑处理[9],但由于构成曲线数据本身的庞大性和复杂性,很难找到一种可以针对不同数据平滑处理的方法。对此,本文提出一种以灰度曲线特征值为依据,设定波峰统计限制条件的方法,实现对机织物密度的测量。
1 密度测量的原理
对所采集织物图像进行灰度处理后,由于经纬纱线的存在,图像在经纬纱线所在地方的灰度值会明显高于间隙处,从而在以纱线为中心的一定宽度范围内形成1个亮度峰值。作出图片灰度曲线后,曲线波峰对应纱线所在位置,波谷对应纱线间隙。但由于杂质信号的干扰,曲线会产生一定数量的杂质小波峰。依据曲线峰值和位置2个特征值,设定波峰统计时的限制条件,就可以准确的统计出波峰个数,从而实现机织物密度的测量,图1为本文方法的测量流程图。
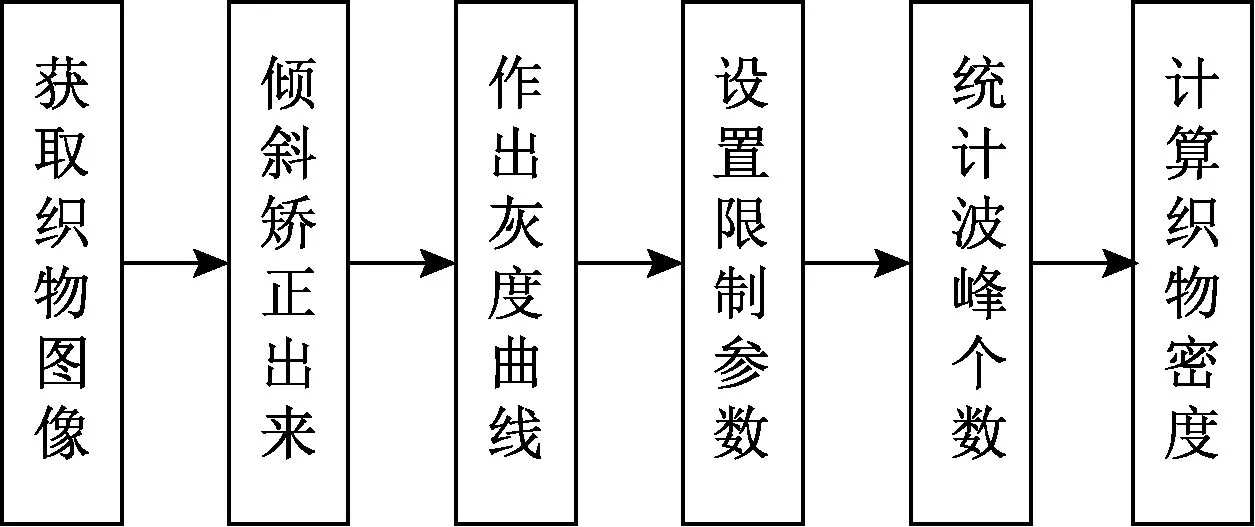
图1 织物密度测量流程图Fig.1 Flow chart of fabric density measurement
2 图像采集与倾斜校正
为了获得质量较好的织物图像,同时更好凸显纱线的存在,本文采用平整且色差较大的黑色纸板为背景,并使用高清摄像头采集图像。在选择织物时,避免织物表面附有大面积的油污、毛羽等[9]。另外,为保证织物表面平整,无褶皱的情况,需要利用夹片对织物施加适当的张力,实验采集的部分图像如图2所示。

图2 部分实验织物图像Fig.2 Images of some experimental fabrics. (a)Color fabric;(b) Solid color fabric 1; (c) Solid color fabric 2; (d) Solid color fabric 3
在织物密度的实际测量中,织物灰度图像的每一行或列应只有纱线或者纱线间隙的灰度信息。当图片倾斜时,会造成这2种信息在该行或者列中大量混合,从而产生较多的杂质波峰,不利于波峰个数的统计。因此在作出图像灰度曲线前,要利用Radon变换对其做倾斜矫正处理,保证图片的倾斜角度在5°以内[10]。Radon变换原理如式(1)所示:
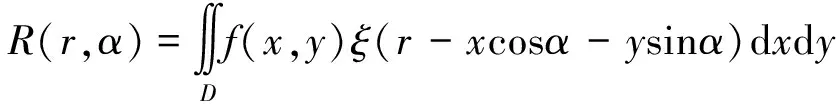
(1)
式中:D为图像平面,f(x,y)为某一点的灰度值;x、y为该点的像素横、纵坐标值,px;ξ为狄克拉函数,r为点(x,y)到原点的距离,px;α为过原点直线的垂线与横坐标轴的夹角,(°)。
特征函数ξ可以保证积分过程沿特定方向上进行,也可以理解为将图像顺时针旋转,对每个旋转角度垂直方向上所在列像素点的灰度值累加求和,当求和值达到最大时对应的旋转角度就是图像的倾斜角度。
矫正前后织物灰度曲线图如图3所示。由图3(a)可以看出,倾斜矫正处理后,灰度值曲线中大部分局部极值被过滤掉,杂质波峰明显减少,灰度曲线也变得相对平滑,但由图3(b)的放大图可知,曲线仍然留有少部分的杂质波峰,这是下文中波峰个数统计时需要解决的重点。
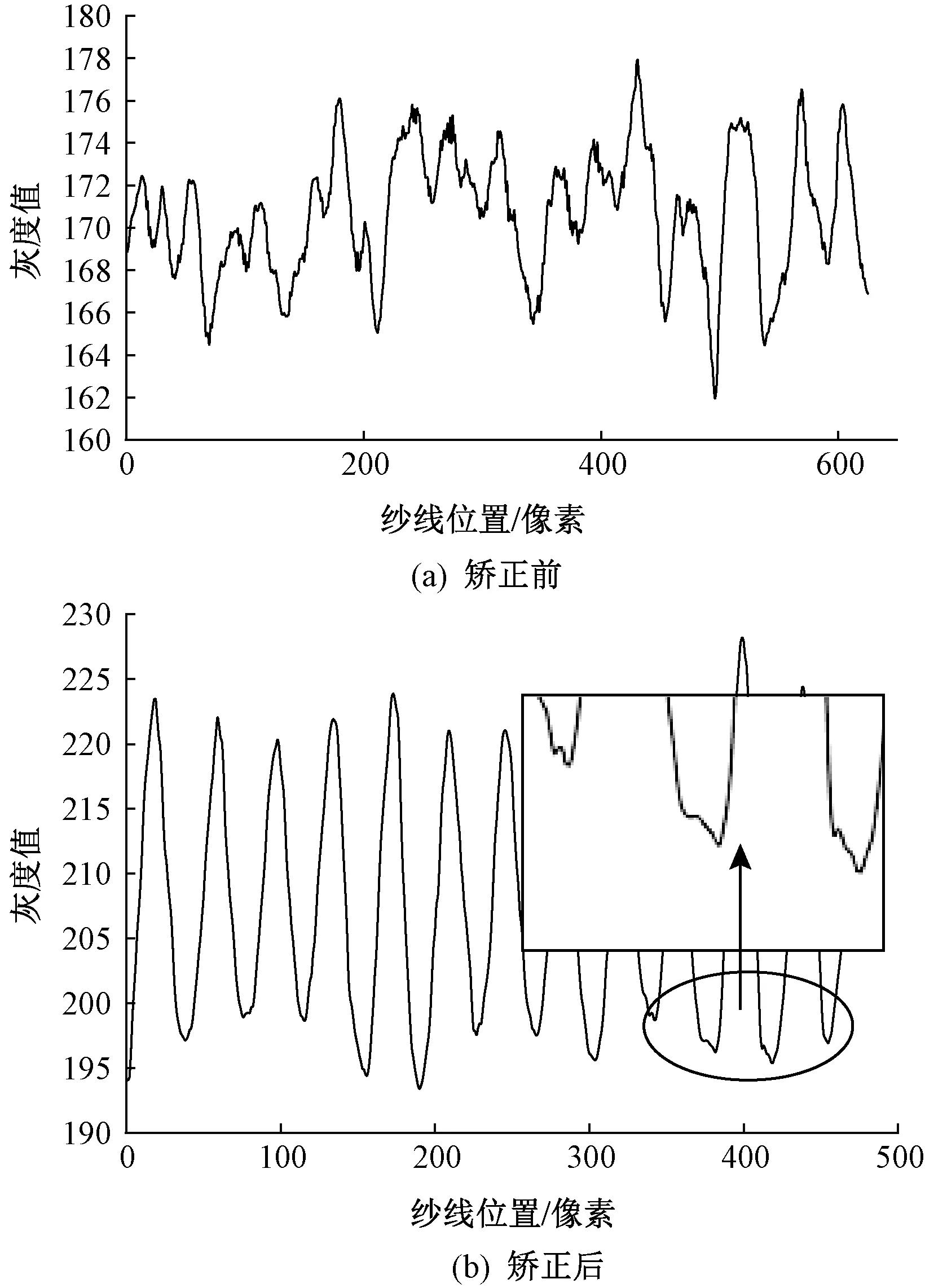
图3 矫正前后织物灰度曲线图Fig.3 Gray curve of fabric image before and after tilt correction. (a) before correction; (b) after correction
3 波峰个数的统计
在作织物图像灰度曲线时,为减少纱线自身存在的疵点、毛羽以及图像录入时产生的信息误差等原因形成的干扰信号,本文以图像每一行或列灰度的平均值为纵坐标,其计算公式如式(2)所示:
(2)
式中:N为图像行或列像素点个数,f(x,y)为灰度值。
提取织物灰度曲线后,可以得到曲线波峰的峰值(纵坐标)以及波峰位置(横坐标)2个特征值。但在统计时必须过滤掉杂质波峰,故本文分别从横纵2个坐标来设置波峰个数统计时的限制条件,实现对杂质波峰的过滤,并探讨更优。
3.1 峰值限制条件的设定
通过提取100幅图像的灰度曲线,对杂质波峰存在位置及其频率进行统计。表1为杂质波峰分布的位置及其对应频率,依据杂质波峰的峰值分布特点,设定限制条件。如当杂质波峰出现在曲线中间与波谷附近时,其峰值与主波峰峰值差值较大,故以所有波峰峰值平均值为界,只计算平均值之上的峰值个数就能准确获得波峰个数。但此方法是获得曲线后的人为经验判断,在实际中无法运用严格统一的鉴别标准。此外,该方法仅适用于简单的平纹纯色织物。某花色织物及其对应的灰度曲线图如图4所示,图4(b)中曲线波峰呈分段集中分布,这是由于不同颜色纱线的灰度值相差较大,且相同颜色纱线分布集中导致的,在这种情况仅凭峰值特点难以准确区分出杂质波峰,故该方法难以运用到实际生产中。

表1 杂质波峰分布位置及频率Tab.1 Impurity peak distribution location and frequency
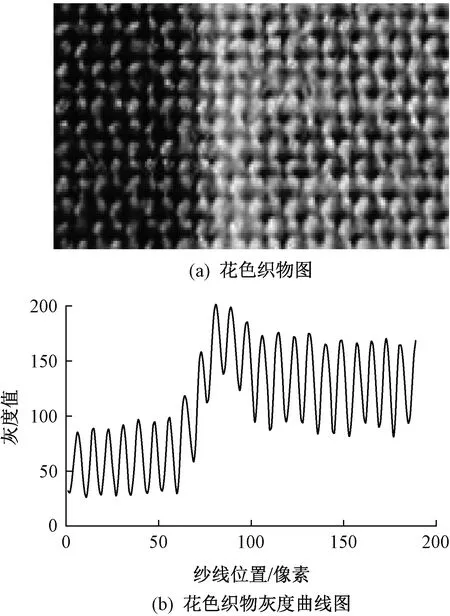
图4 某花色织物Fig.4 A patterned fabric. (a)A patterned fabric picture; (b) Gray-scale curve diagram
3.2 位置限制条件的设定
虽然曲线波峰的峰值会由于机织物的结构、花色以及数据本身的庞大而变得复杂多样,难以用同一种标准或方式设定波峰统计时的限制条件。但如图4所示,对波峰的位置(即横坐标)没有影响,相邻波峰之间的宽度依然基本相等[11],这是由机织物纱线分布均匀稳定的特性决定的。因此对于任意一个织物图片曲线,相邻波峰间的宽度只存在有限个可能。而在理论上,曲线在一定宽度(此宽度约为曲线周期)范围内只应该存在1个波峰。统计各个间距值以及对应的频率,以此设置一个限制条件K,规定相邻波峰之间的距离必须大于设定值K,否则在记数时将峰值较小者过滤,只统计峰值较高者,如此便可准确统计织物纱线根数。间隔值K的具体设定方法步骤如下:
①记录灰度曲线所有波峰的信息,即每个波峰点的横坐标与纵坐标。
②利用逐差法计算所有相邻2个波峰的间距,其计算公式如式(3)所示。然后统计各个间距值的频率并按照降序排序,记间距值为Ki,对应频率为Pi,i=1,2,3,…。
D=g(x(2∶i))-g(x(1∶i-1))
(3)
式中:g(x)为波峰的位置,i表示波峰次序,即第i个波峰。
③根据波峰间距的频率分布情况确定间隔值:
若P1>0.5,K=K1;若0.5>P1>0.3,K=(K1+K2)/2;若P1<0.3,且K1、K2、K3之间的极差小于等于4,K=(K1+K2+K3)/3。
特别地,若波峰间距频率分布情况不属于以上3种,这极大可能是由于倾斜矫正不到位、图片质量模糊或纱线毛羽疵点过多造成的,可以将实验结果直接输出为0,以提醒操作者对该图片重新拍照检测。
在实际的密度测量中,K值与曲线周期接近,若直接取该值,会由于间隔值设置过大而过滤掉部分主波峰,降低实验结果准确率。为了过滤在谷底附近的杂质波峰,该值必须大于K值的1/2。最后经实验证明,当取K值的2/3时,实验结果稳定且准确率较高。
4 实验结果及讨论
本文实验采用100多块经纬密度不同的机织物样品进行经密和纬密的测量,为验证本文方法的准确性,在采集织物图片以及预处理时,会保证纱线的倾斜度不超过5°;同时每块布样不同位置测3次,取平均值作为人工检查的结果与图像检测所得结果对比,二者误差计算公式见式(4),部分实验结果如表2所示。
(4)
式中:d1、d2分别为图像检测和人工检测所得结果,根/(10 cm)。
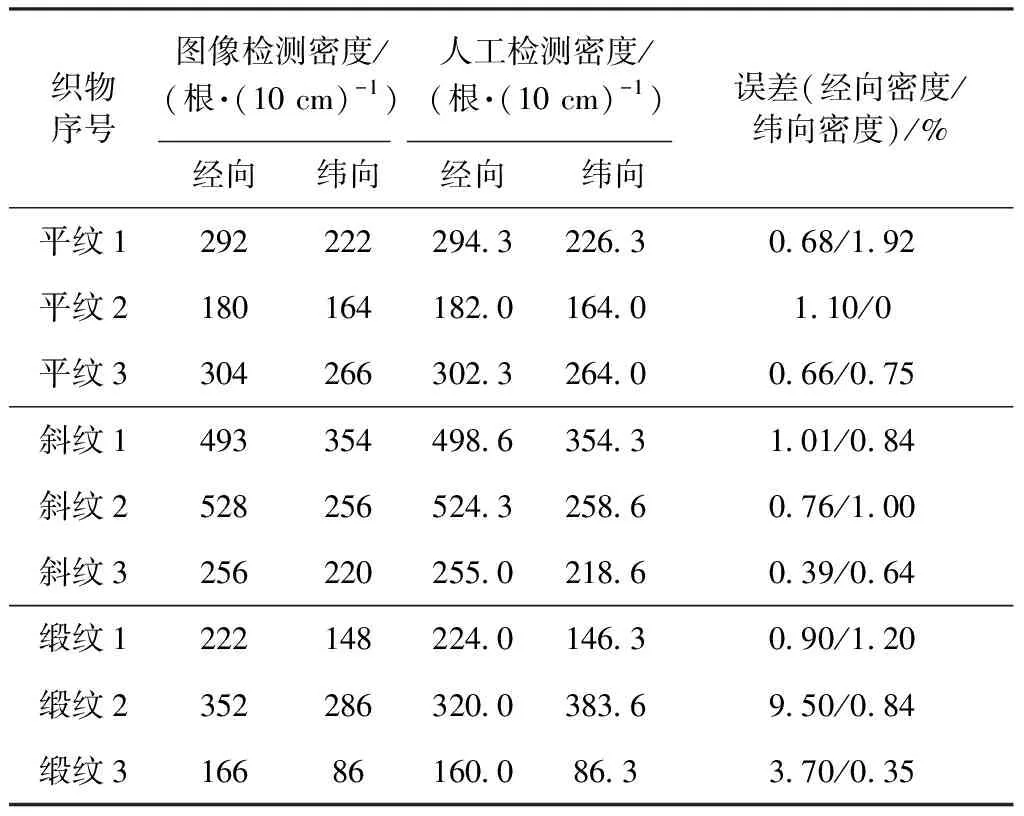
表2 图像检测与人工检测结果对比 Tab.2 Comparison of image detection and manual experiment results
由表2示出,在实际测量时,平纹织物和斜纹织物由于其组织结构相对简单,实验最大误差为1.92%。且经计算,经向密度、纬向密度的平均误差分别为0.77%、0.86%,二者均小于1%,整体上在2%的误差允许范围内,实验结果可信度较高。但对于缎纹织物,检测结果的准确性存在较大波动,如缎纹2中,经密最大误差可达接近10%,但在缎纹织物的纬向密度测量中,误差却能保持在2%以内。对此,在未来的实验中需要对检测方法作进一步改进,提高对复杂织物检测结果的准确性,扩大本方法的使用范围。
5 结 论
实验表明,在设定灰度曲线波峰统计限制条件时,波峰的位置分布比峰值分布更具有规律性,更利于该条件的设置;当宽度间距K为原定值的2/3时,实验结果的准确性和稳定性达到最高。同时,图像检测时间较人工检测也有了极大的缩减,同时还能基本满足花色织物密度实际检测的需求。但对织物组织相对复杂的缎纹织物,其经向密度的检测结果有较大的波动,这是本文以后需要改进的地方。

