基于BP神经网络的童装流行元素预测
刘妍兵,刘伦伦,唐 颖,2
(1.江南大学 设计学院,江苏 无锡 214122; 2.米兰理工大学 设计学院,意大利 米兰 20158)
近年来,随着互联网和大数据分析技术的普及与应用,智能计算工具在时尚界被广泛应用[1]。目前,时尚流行趋势预测的界定方法主要以定性方法为主,依赖经验和直觉判断流行趋势,存在着一定的局限性和盲目性[2]。通过按照一定规则梳理和汇总童装流行元素信息,建立数学分析模型,可量化童装流行元素并加大其区分度,从而减少设计师在童装设计中对主观感觉和经验的依赖,以达到依靠数据分析结果进行童装流行元素预测的目的。长期以来,为了更好地解决定性预测法中设计决策锚定出现偏差等问题,许多研究以流行元素为研究对象,通过一定的数学工具,针对流行元素中可以量化的部分进行测量和分析。关于流行元素的理论预测模型中最具有代表性的主要有灰色系统理论[3]、人工神经网络模型[4]和自回归综合移动平均值(ARIMA)[5]等传统的数理统计模型。
人工神经网络不仅具有很强的并行处理、自学习和自适应等能力,还拥有十分灵活的非线性建模功能。与统计数据处理模型不同,人工神经网络不假设数据模式,只要有足够的历史数据点、使用适当的人工神经网络结构,就可以预测任意数据模式。
本文以数据量化技术和BP神经网络预测技术为理论基础,初步建立了童装流行元素预测模型,对童装流行元素进行了综合分析和预测。同时,为了改善传统的BP神经网络算法收敛速度慢、易陷入局部极小值等情况,在构建神经网络中逐步增加训练数据、隐藏单元优化算法。并加入1个动量项以降低误差曲面局部细节的敏感性,克服网络容易陷入局部极小的缺点、提高预测精度。在历史数据很少的情况下做出合理的预测决策,辅助童装设计师精准把握童装流行方向。对于童装设计生产过程中,童装的流行趋势预测具有实际意义。
1 BP神经网络预测算法
BP神经网络是一种有效的多层神经网络学习方法,其特点是信号向前传递,误差反向传播,之后用这些误差来调整神经元的权重,从而生成一个可以模拟出原始问题的人工神经网络系统[6]。
童装流行元素的变化受到人的主观判断(或称为专家建议)和文化、经济、政治等外部因素的影响。在高度波动的时尚销售时间序列中可能没有明显的趋势和周期,因此传统模型在历史数据很少的情况下做出合理的预测决策具有较大的挑战。本文面对童装流行元素预测领域中有限的历史数据,对比分析后选择BP人工神经网络预测模型进行研究。
图1为一个输出变量的BP神经网络的拓扑结构图。在该网络中,存在Xi为输入层向量,Dk为输出层向量,以及他们之间的一个或多个隐藏层由Zi来表示;Wij、Wjk分别表示输入层到隐藏层、隐藏层到输出层的连接权值。
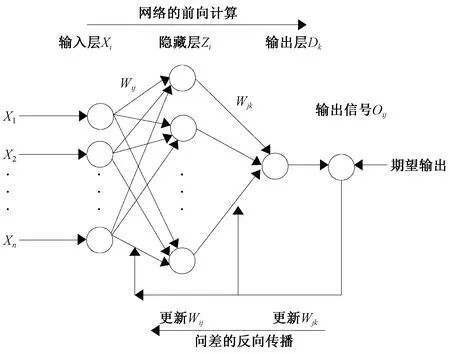
图1 BP神经网络拓扑结构Fig.1 BP neural network topology
BP神经网络典型算法的基本公式如下[7]:
(1)
(2)
式中:Xi为神经网络输入值;Yi为实际神经网络输出值;di为神经网络的期望输出值;Wijk为第i层第j个神经元到第i+1层第k个神经元连接权值;Oij为第i层第j个神经元输出值;θij(或θij)为第i层第j神经元的阈值;netij为第i层第j个神经元总输入。
BP算法基于误差函数的梯度信息,当问题复杂或难以获得梯度信息时,BP算法就会存在局部极小值。BP神经网络的收敛性通常取决于经验,学习因子和惯性因子的选择也会影响BP神经网络的收敛性。为了克服这些缺点、改善BP的收敛速度、提高神经网络的泛化能力,在神经网络的研究和设计中导入了许多优化算法。本文采取Rumelhart等[8]提出的逐步增加训练数据和隐藏单元优化算法构建神经网络,通过加入动量项,降低了误差曲面局部细节的敏感性、克服网络容易陷入局部极小的缺点,提高预测精度。计算当前误差曲面的负梯度变化量与前一次迭代修正所采用的权值变化量的适当比例求和,获得权值的变化量,计算公式见式(3)。
ΔW(t)=ηδO+αΔW(t-1)
(3)
式中:W为某层的权矩阵;η为学习率;α为加权和的权重;O为某层的输出向量;δ为误差项,即δ0是O的误差值。
图5表明了使用自适应阈值,检测结果比整个图像的固定阈值稍差。另一个方法尝试通过调整阈值来改进SUSAN算法,结果亦能够得到一定的改善。由于该类算法主要采集检测建筑物边缘和角点特征,所以,对其检测步骤进行细化,能够提高检测准确度,消除虚假警报并恢复错过的特征信息。在拐角的情况下,特征之间彼此不连通,使用边缘信息理论以实现建筑物特征点稀疏化的过程。
2 预测模型实现分析
2.1 童装流行元素样本数据库建立与元素识别
在未来儿童服装流行元素趋势预测中,童装的廓形数据、色彩数据、面料数据、辅料数据、图案数据、工艺数据等时尚信息常被用作基础的历史数据库。在现代社会中,童装的流行受到社会文化和社会现象的影响,人们获取的童装流行元素往往是以不完整的文字、图片、影像等多元化形式的资料呈现,设计师们很难进行有效的流行元素识别。
针对这种情况,进行了童装流行元素的提炼:把相关流行消息的相互影响结果嫁接在童装产品的具体构成元素中去,找到各个领域之间的内部联系,并从事物的意识形态和社会文化视角去审视童装的流行要素,从而探索时尚的来源和实质,对童装流行元素的发展趋势进行更加准确的把握。本文从中国主要电商平台的童装品牌销售数据、服装市场数据中获取样本数据,从童装流行元素的整体风格入手,行之有效地把童装的流行元素逐一提取出来,并按照造型要素、款式要素、材料要素、色彩要素、图案要素、结构要素、工艺要素、搭配要素和风格要素这九大类进行分类[9],流行元素识别的流程如图2所示。

图2 流行元素识别的流程Fig.2 Process of identifying popular elements
2.2 数据量化方法
量化可以将成千上万的信息转换成数据形式,是所有数据的核心[10]。在进行童装流行元素量化研究过程中,采用虚拟变量的方法,对已分类的童装流行元素进行量化,着重探讨客观购买行为与有关变量的因果关系和变量间的相关性。采用数值的形式分析童装流行元素,为童装设计提供一定科学性的参考。
量化研究包含几个相互关联的步骤,各个步骤环环相扣[11]。实现量化需要把已知的历史数据量化成可参考、对比、分析、建模的数据资源。目前童装设计所呈现的信息多且杂乱,利用海量信息概括出普遍规律、从而对童装的流行元素进行预测是量化研究的核心问题之一。
本文的量化研究包括假设、实验验证和数据分析3个阶段。第1阶段通过制定研究目标、选取研究对象、分析相关变量作为整个量化研究的基础。第2阶段主要是多渠道客观、科学地获取实验数据资料。第3阶段是数据的计算机化分析,其主要目的是把看似杂乱无章的数据进行萃取、提炼,以找出童装流行元素的内在关系。具体的量化研究方法如图3所示。
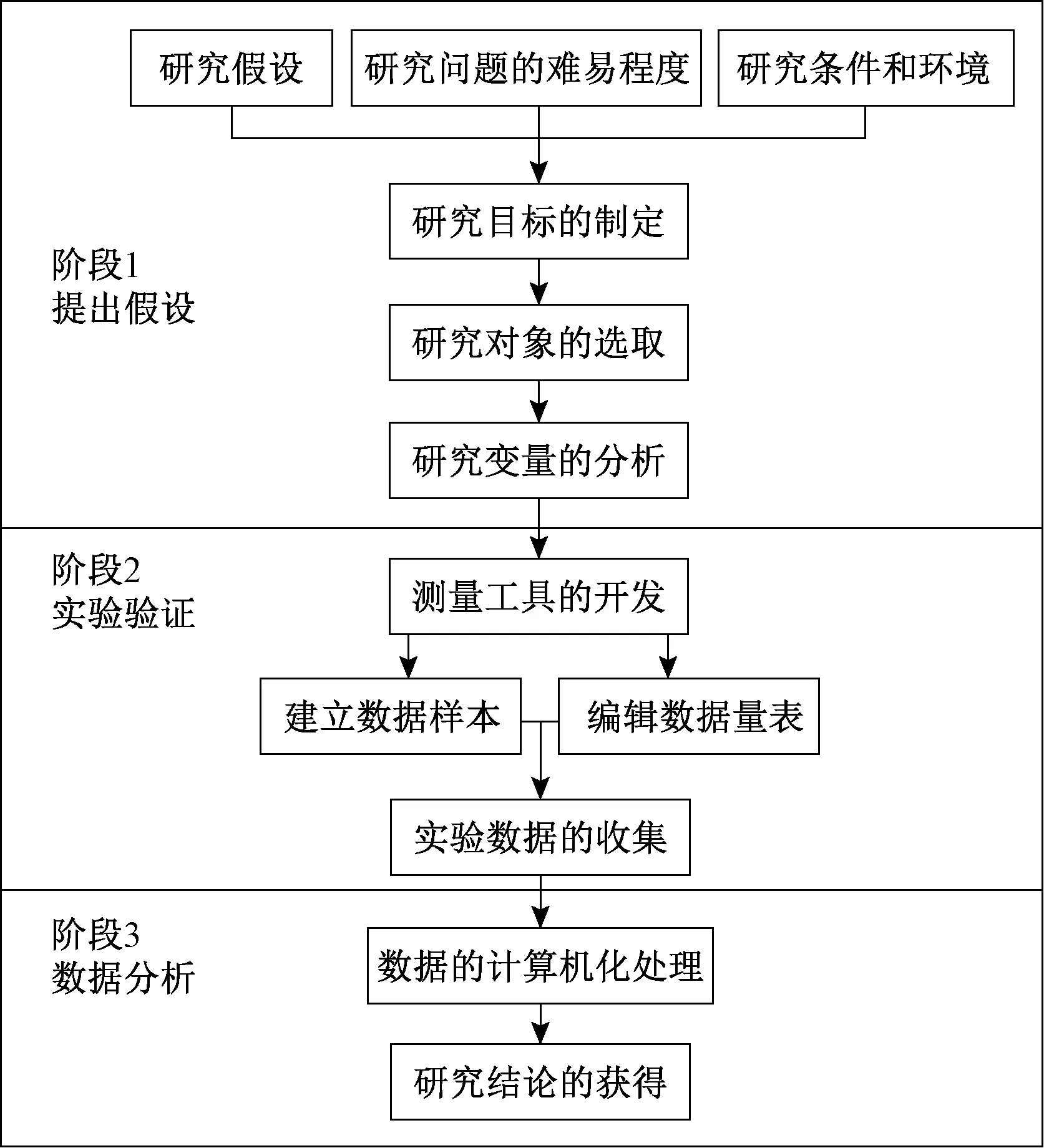
图3 量化研究的基本方法Fig.3 Basic methods of quantitative research
2.3 童装流行元素预测流程
采用BP神经网络模型预测童装流行元素,图4为BP神经网络童装流行元素主要预测流程。首先按照一定的规则将童装流行元素进行汇总和梳理,以历史销售额占比作为反映流行程度的指标,采用虚拟变量的方法对分好类的童装流行元素进行归一化处理,使收集到的图片和文字型数据转化成为可以量化的数据;然后,以输入、输出矩阵的形式确定预测元素的样本数据,且对数据样本进行散点绘图,对童装流行元素的整体趋势走向、规律、周期等形成初步判断;接着对样本数据网络进行训练,调整隐含层节点数,以BP神经网络模型模拟预测结果,对童装流行元素进行预测并输出。最后,验证和检验预测结果。

图4 BP神经网络童装流行元素预测流程图Fig.4 BP neural network children′s fashion element prediction flow chart
3 童装流行色预测实例

表1 2000—2019年色相历史数据Tab.1 Historical data of color hue from 2000 to 2019
原始数据中不同流行色对应的销售额以及不同年份的销售额之间存在量纲差异较大现象,针对建模过程中可能出现“大数吃小数”等造成最终预测模型解释性和预测能力不足的现象,首先对原始数据进行归一化处理,即将每年不同色彩元素销售额数据样本标准化为0~1区间内,得到一定的标准化之后的数据表格。2000—2019年色相历史数据见表1。表格虽然可以对历年不同色彩元素的销售情况、流行程度进行精确描述,但是其信息呈现比较分散且不够直观。为了定性且直观地分析色彩元素的变化规律和整体特征,又绘制了不同色彩明度、纯度每年销售额占比的变化趋势,以及其在过去20 年内的销售额累积占比,不同明度销售额占比变化见图5,不同纯度销售额占比变化见图6。
表1及图5、6示出,销售额占比可以反映流行程度,不同色彩元素流行程度随年份波动而变化且具有周期性。基于色相元素销售情况变化周期基本为3年,将BP神经网络的输入节点选择为3;明度的变化周期为4,纯度变化周期为3,将明度和纯度神经网络训练模型的输入时间节点选择为4和3。
基于上述数据进行BP神经网络建模和预测,对色彩三要素的模型训练过程如图7所示。将已知信息和基于历史数据中的流行色分析判断作为先验信息,对BP神经网络建模预测效果进行参考和验证。

图5 不同明度销售占比变化折线图Fig.5 Line graph of the change in the percentage of sales by brightness.(a)High lightness sales; (b)Medium lightness sales;(c) Low lightness sales

图6 不同纯度销售占比变化折线图Fig.6 Folding graph of the change in the percentage of sales of different purity levels.(a)High purity; (b)Medium purity;(c)Low purity

图7 色彩三要素的BP神经网络模型结构Fig.7 Model structure of BP neural network model with three elements of colour.(a) Hue;(b) Lightness;(c) Purity
由图7示出,3个模型均可以在有限步骤之内结束,且满足在误差允许范围内。对色彩三要素训练的性能曲线如图8所示。

图8 色彩三要素的BP神经网络模型性能曲线Fig.8 Performance curve of the BP neural network model for the three elements of colour.(a) Hue;(b) Lightness; (c) Purity

图9 色彩三要素的BP神经网络模型误差直方图Fig.9 Error histogram of the BP neural network model for the three elements of colour.(a) Hue;(b) Lightness; (c)Purity
3个模型预测误差直方图如图9所示。由图9示出,模型误差主要分布在0误差线附近,而且近似呈现标准正态分布曲线,可以理解为影响色彩流行程度的不可测白噪声因素。在预测建模领域,将不可控不可测的未知自变量纳入噪声因素,但是可以通过分析噪声的分布类型来确定建模效果,根据大数定律和中心极限定理,变量一般服从正态分布。图9中的均值为零的正态分布则表明模型精度较高且符合客观事实。基于上述模型对2021—2022年秋冬童装流行色的色相预测显示,黄色的流行度最高,占比0.287 7%,其次为红色,占比0.139 1%,黑白灰则占比最少为0.009 1%,具体结果如表2所示;对明度流行预测显示,高明度流行度最强,占比为62.75%,中明度次之为21.91%,低明度为15.34%;对纯度流行预测显示,中纯度流行度最大,占比为62.17%,低纯度次之为24.84%,高明度为12.99%。
在2000—2020年共20年历史数据训练出的BP神经网络预测模型的基础上,对2021—2022年童装流行色进行分析,发现2021—2022年秋冬较为流行的色相为:黄、黄红、红,与市场流行趋势一致,表明2021—2022年秋冬流行色相具有继承性且预测模型较为可靠。红紫和蓝绿2种色相的流行程度将在2021—2022年秋冬大幅提升,可作为市场营销的指导信息,反映出人们对于色相追求更加多元化的潜在趋势;高明度依旧是2021—2022年秋冬最流行的色彩特征,从侧面体现了儿童对于鲜亮外表的追求心理;而纯度流行趋势则在2021—2022年秋冬将发生大幅变化,中纯度将形成压倒性流行态势,这与当下童装更替速率加快,大众更愿意降低纯度要求、提高了对其他元素要求的现象有关。

表2 2021—2022年秋冬童装色相流行预测Tab.2 Autumn/winter children′s clothing colour palette trend forecast 2021—2022
4 结束语
本文以数据量化技术和BP神经网络预测技术为理论基础,初步建立了童装流行元素预测模型。利用童装BP人工神经网络预测模型,对童装流行元素的整体趋势走向、规律、周期等形成了初步判断,之后选定色彩元素作为预测指标构建了预测模型实例,对样本数据进行训练,调整其隐含层节点数,以BP神经网络模型模拟预测结果,从而对2021—2022年秋冬的流行色进行预测并输出符合市场流行趋势。该模型将人工智能和设计人员的经验相结合,有助于帮助服装设计师把握流行方向,对市场营销和产品设计具有重要的参考价值和指导意义。
——兼论八色相环的内涵

