基于改进探路者算法求解0-1背包问题
张小萍,谭欢
(1.广西大学 计算机与电子信息学院,广西 南宁,530004;2.中国移动通信集团广西有限公司,广西 南宁,530022)
0-1背包问题是运筹学中一个经典的NP-hard问题。生活中有很多难以求解的问题,例如投资决策、货物装载和资金预算等问题都可以转化为0-1背包问题,因此,0-1背包问题在理论研究和实际应用中都有比较重要的意义。传统求解0-1背包问题的方法主要是确定性算法,例如分支定界法、穷举法和递归算法等。确定性算法的主要优点是一定能够求出问题的最优解,但其缺点是算法的时间复杂度随问题的规模呈指数增长,因此,该类算法只能用于求解小规模的0-1背包问题。与传统算法相对的是智能优化算法,该类算法的主要优点是求解问题的时间复杂度是多项式的,求解问题的速度快。但其缺点是一般求出的是问题的最优解域,不一定能获得精确的最优解,因此,该类算法可以用于求解大规模的0-1背包问题。一些学者使用智能优化算法来求解0-1背包问题,文献[1]提出了二进制乌鸦算法(CBCSA),利用Chebyshev映射产生混沌序列保证初始种群的均匀分布,然后,使用贪心修复和优化算法(greedy repair and optimization algorithm,GROA)对个体修复和优化,提高种群的收敛速度。文献[2]提出的算法(DCSO)在基本鸡群算法的基础上进行二进制离散化,在公鸡位置更新中使用自适应权重,在小鸡位置更新中使用了定向变异的策略,提高了算法的全局搜索能力。文献[3]提出一个离散改进的人工蜂群算法(DIABC),利用惩罚函数来解决不可行解的问题,改进了工蜂和观察蜂搜索的方式,提高了算法的收敛速度。文献[4]在基本差分算法的基础上,提出了新的rand/3/bin变异策略并结合交叉选择策略来求解0-1背包问题(DE3BINA),获得了较快的收敛速度,但它测试的问题规模较小,为10个维度在4到23的实例,在较大规模的0-1背包问题中的寻优能力未知。文献[5]利用DNA折纸技术结合杂交链式反应来求解0-1背包问题,但它仅在4个物体的0-1背包问题中进行测试,由于DNA折纸基底尺寸的限制,只能用于小规模的背包问题求解,目前难以实用。文献[6]使用线性规划构建因子图模型,利用置信传播算法来求解0-1背包问题,测试显示该算法具有较好的全局搜索能力,但它的测试实例是随机生成的,并且没有公开数据,难以评价算法的寻优精度和跳出局部最优解的能力。
为了进一步提高求解0-1背包问题的寻优效果,利用基本的探路者优化算法提出一个改进算法来求解0-1背包问题。首先,该算法先对种群个体进行二进制编码。然后,采用贪心修复和优化算法对个体进行修复和优化,并使用变异策略对个体进行搅动以提高种群的多样性。最后,使用仿真实验数据对比来说明改进算法是有效的。
1 相关知识
1.1 0-1背包问题
0-1背包的一般描述为:有一个最大承重量的背包,现有n件物品,每件物品有重量和价值,选择将物品装入背包并在不超过背包最大承重的前提下使得装入物品的总价值达到最大。其数学描述如下:
(1)
(2)
其中,vj和wj分别表示物品j的价值和重量;n表示物品数目;C表示背包的最大承重量;Y是一个n维的二进制向量;相应比特位是0,表示该物品未选中放入背包;相应比特位是1,表示选中该物品放入背包。
1.2 基本探路者优化算法
探路者优化算法是 YAPICI等[7]提出的一种新兴的智能优化算法,该算法的思想起源于群体动物的狩猎行为,种群中的个体分为探路者和跟随者两种角色。算法的寻优过程模拟了种群寻找食物的探索过程,利用探路者、跟随者两种角色不同的位置更新方式以及角色间的交流来实现优化,种群三代间的优良信息在迭代过程中也保留下来,能够快速获得较好的解。在种群更新中,探路者是整个种群位置的先行探索者,比跟随者先移动,探路者的位置更新公式为
A=u1e-2k/kmax
(3)
(4)

跟随者的位置更新公式为
(5)

基本探路者算法的步骤为
1)初始化系统参数。
2)初始化种群,计算出种群中个体的适应度值,适应度最优的个体成为探路者,其他个体是跟随者。
3)使用公式(4)对探路者位置进行更新。
4)使用公式(5)对跟随者位置进行更新。
5)计算种群中所有个体的适应度值,计算出全局最优解,并重新确定探路者和跟随者。
6)判断是否符合结束条件,符合就输出全局最优解,否则回到步骤3。
探路者算法具有便于理解、算法简单、优化性能良好等优点,探路者算法及其改进算法被已用于多个应用领域。文献[8]利用混合探路者算法求解有限缓冲区和带能耗阈值约束的绿色流水车间调度问题,获得了良好的改进效果。文献[9]针对医疗影像处理问题,提出一种基于探路者智能搜索算法,该算法能提高图像识别的效率和准确率。文献[10]利用改进的探路者算法和样本熵进一步优化集成学习模型,利用优化模型预测PM2.5的浓度,实验表明,优化模型在稳健度和预测准确度都高于其他基准模型。文献[11]将探路者算法用于软件预测缺陷模型,利用探路者算法优化神经网络的权重值,提高了软件预测缺陷的准确率。文献[12]利用维度学习策略改进了探路者算法求解函数优化问题,对越界和迭代不成功个体采取了加强维度学习的策略,测试表明,改进的算法优于其他对比算法。由于探路者算法提出时间不长,应用领域还不够广泛,还没有被用于求解0-1背包问题。
2 改进探路者算法求解0-1背包问题
2.1 二进制编码
基本探路者算法求解的是连续型的问题,而0-1背包问题是二进制离散型的问题,因此,要先对个体进行二进制编码,假设有一个连续型数据的向量X=(x1,x2,…,xn),编码为二进制向量Y=(y1,y2,…,yn),编码规则如下:
(6)
2.2 贪心修复与优化算法
由于0-1背包问题要满足公式(2)的约束条件,因此,在对个体进行二进制编码后得到的只是问题的潜在解,对于不满足公式(2)的不可行解,目前在0-1背包求解中有两种处理方法:一种是使用惩罚函数来减小其适应度;另一种是使用贪心修复与优化算法。总的来说,使用GROA比使用惩罚函数要好,因为GROA不仅可以将不可行解修复为可行解,而且可以对可行解进行优化,这将大大提高算法的收敛速度。GROA的过程分为两个步骤:第一个步骤是进行修复。若一个解是不可行解,优先将价值与重量比值较小的物品移出背包,这个过程不断重复,直到背包中物品的总重量小于背包的最大承重量为止,经过这个步骤的修复,不可行解就变成了可行解。第二个步骤是进行优化。在没有超过背包的最大承重量的前提下,优先将价值与重量比值较大的物品装入背包,不断重复这个过程直到尝试到最后一个物品。GROA具体算法的伪代码可以参考文献[1]。
2.3 变异策略
借鉴遗传算法中变异的思想,为了避免种群僵化,增加种群个体的多样性,以一定的变异概率pv对个体进行变异,每次变异随机选中个体二进制向量的3个比特位,将这3个比特位由0变成1或者由1变成0。
2.4 改进探路者算法(IPFA)求解0-1背包问题步骤
1)初始化系统参数。
2)初始化种群,对个体进行二进制编码,使用GROA修正和优化编码,计算出种群中个体的适应度值,适应度最优的个体成为探路者,其他个体是跟随者。
3)使用公式(4)对探路者位置进行更新,对探路者位置进行二进制编码,使用GROA修正和优化编码。
4)使用公式(5)对跟随者位置进行更新,对跟随者位置进行二进制编码,使用GROA修正和优化编码。
5)对所有个体的二进制编码用变异策略进行变异。
6)计算种群中所有个体的适应度值,计算出全局最优解,并重新确定探路者和跟随者。
7)判断是否符合结束条件,符合就输出全局最优解,否则就回到步骤3。
IPFA的算法流程见图1。

图1 IPFA算法流程图Fig.1 IPFA algorithm flow chart
3 仿真实验数据分析
为了验证提出算法的性能,使用文献[2]中的4个维度,即分别为20,50,80和100的0-1背包实例作为测试数据,与CBCSA,DCSO和DE3BINA 3个算法做比较。在实验中,本文提出算法的变异概率pv设为0.1,其他算法的参数按照相应算法的文献来设置。仿真实验环境设置如下:操作系统为64位的Windows 7,内存为8G,编程环境为MATLAB R2020b。为了保证公平性,所有算法的迭代次数都设为200次,种群的个体数量为50个,每个算法单独测试20次,分别计算出每个算法获得的最小值、最大值、平均值、方差和运行时间等信息,rate表示实验中算法获得理论最优值次数占总实验次数的比例;rank是对算法排名,将平均值大的排在前面,平均值相同的就比较运行时间,将运行时间少的排在前面。具体获得的数据见表1。
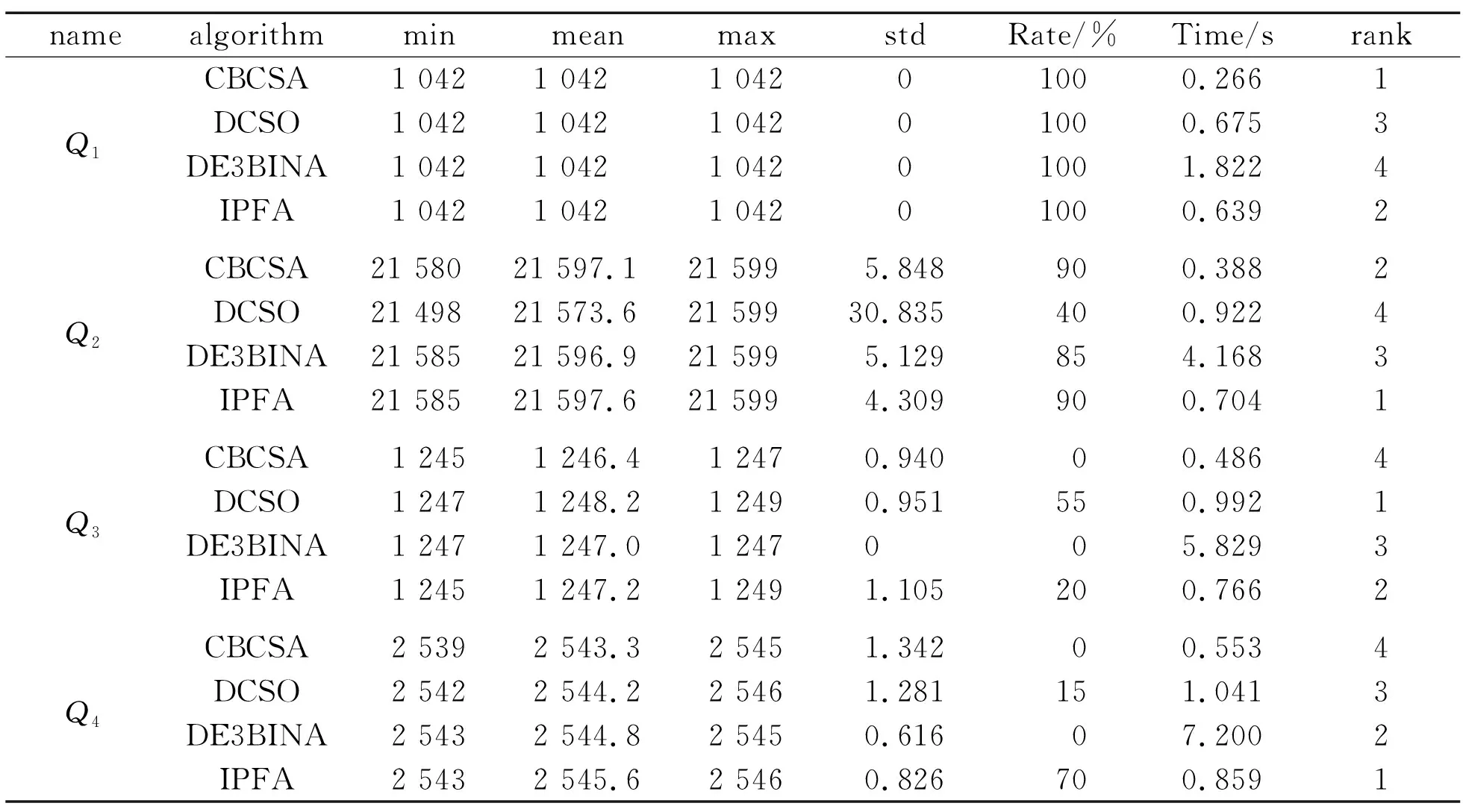
表1 仿真实验结果
从表1中可以看出:IPFA在Q1的实验中每次都能找到最优值,只是运行时间比CBCSA要大一些,但比其他两种算法都快。在Q3中平均值仅次于DCSO,它命中理论最优值的概率比DCSO要小一些,但是比其他两种算法命中最优值的概率要高,而在Q2和Q4中,从平均值的情况看,IPFA是4种算法中最好的。计算CBCSA,DCSO,DE3BINA和IPFA在4个测试案例中的平均rank值,分别得到2.75,2.75,3.00和1.50,显然IPFA的平均rank值是最小的,说明它在4种算法中的寻优效果最好。计算CBCSA,DCSO,DE3BINA和IPFA在4个测试案例中的平均std值,分别得到2.033,8.267,1.436和1.560,IPFA的std平均值仅大DE3BINA一点,但DE3BINA的平均rank值是最大的,而且运行时间是4个算法中最大的。
图2~5给出了4个算法在各个测试案例中的收敛曲线,从图中可知:IPFA在Q1,Q2和Q4中都比其他算法要更快地迭代到最优解,在Q3中只有IPFA和DCSO收敛到了最优解,但IPFA需要的迭代次数更少,具有较快的收敛速度。

图2 Q1的收敛曲线图Fig.2 Convergence curve of Q1
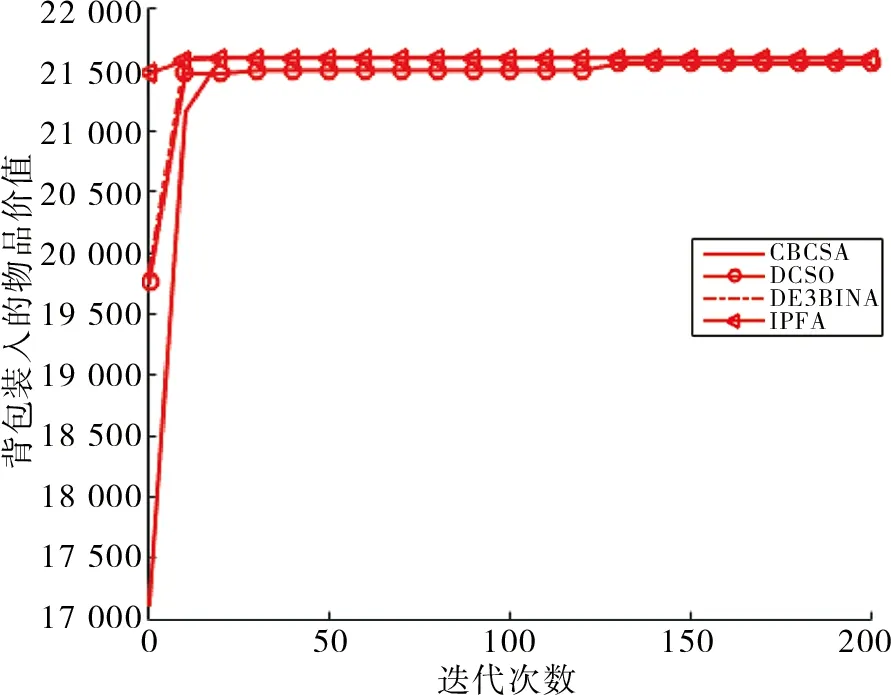
图3 Q2的收敛曲线图Fig.3 Convergence curve of Q2

图4 Q3的收敛曲线图Fig.4 Convergence curve of Q3
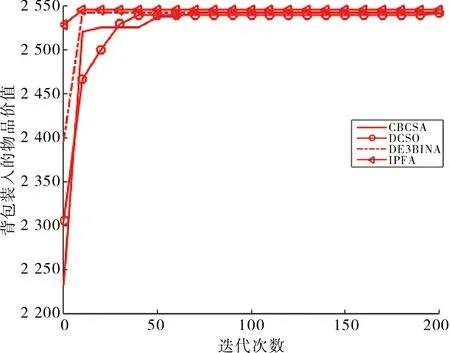
图5 Q4的收敛曲线图Fig.5 Convergence curve of Q4
4 总结
本文提出一种改进的探路者算法求解0-1背包问题,通过二进制编码将连续性问题变为离散化问题,利用GROA加强了局部开发,进一步提高了算法的收敛速度,结合使用变异策略,增加了种群的多样性,加强了算法全局勘探能力,避免了早熟和陷入局部最优解,几个改进策略较好地平衡了算法勘探和开发的能力。通过对4种不同维度测试案例的仿真实验表明,与其他3种算法对比,IPFA具有一定的优势,即收敛速度快、寻优效果好、稳定性高。改进探路算法也拓宽了探路者算法的应用领域,是一次有益的尝试。IPFA每次在每个位置更新时都要使用贪心算子,这样做虽然加快了算法的收敛速度,但是比较耗费时间,难以适用于更大规模的0-1背包问题(例如500维以上)。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

