关于ENSO事件监测指数的改进方案

陈璇 郑崇伟 郝全成 吴雪剑

(1 广东省气候中心，广州 510507; 2 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室，北京100029; 3 中国海洋大学山东省海洋工程重点实验室，青岛 266100; 4 中国人民解放军75839部队，广州 510510;5 海军大连舰艇学院，大连 116018; 6 中国人民解放军94865部队，杭州 310017)

引言

厄尔尼诺/拉尼娜(ENSO)事件是气候系统年(代)际变化的标志性事件，与我国夏季降水[1-5]、亚洲冬夏季风[6]、西太平洋热带气旋[7-8]、印度洋海盆海温[9]、热带海表温度[10]等均有紧密关系。龚道溢和王绍武[11]分析了近百年的El Nino C区各月海温距平与全球降水和中国降水之间的关系，其中，援引了臧恒范和王绍武[12]的相关工作，臧的工作中凸显了部分关于事件定义的分歧。然而，这种分歧仅限于资料的准确度。

2017年，中国气象局发布了厄尔尼诺/拉尼娜事件判别方法的国家行业标准(QX/T 370—2017)[13]，此前，也有关于ENSO指数的相关研究[14-15]，这些研究均涉及参考年的选取。该标准援引世界气象组织相关推荐，定义了气候标准值的选取、替换流程。目前，国际和国内通行的监测方案是依托距平指数对相关年份进行分类；距平指数的计算需要气候标准值。由于气候标准值每10年均要进行滚动更新，这导致该标准值却是非恒定的。在国家气候中心的相关网页上，公布了ENSO事件特征量综合表(http://cmdp.ncc-cma.net/download/Monitoring/Sea/ENSO_Characteristic_Table.pdf，气候标准值为1981—2010)和ENSO历史事件统计表(http://cmdp.ncc-cma.net/download/ENSO/Monitor/ENSO_history_events.pdf，采用30年滚动的方式计算气候标准值)。对于1951年以来的ENSO事件，两组统计数据存在一定的差异，对应事件的起始终止时间、峰值、峰值月份、强度等级以及事件类型均存在一定差异。

该标准并未提出在不同气候标准值下，厄尔尼诺/拉尼娜事件不一致的情形该如何处理；取而代之的是强调了计算方式的滚动性质。这种处理方式虽然固定了事件的性质、历史序列重构方式，但在长期序列处理过程中，仍然存在一些问题。例如：2000年前后处于气候标准值更换的年份，但从时间连续性上来说，这段时间的ENSO监测值应当具有连贯性；然而更换参考年，对应的事件性质(发生中断，且强度变化幅度较大)则发生了一些变化(表1)。

表1 国家气候中心公布不同参考年部分ENSO事件起止时间和强度对比

从大气环流的角度上来说，海表温度异常偏高或偏低应当属于海温的内秉属性，即不随外界标准值的变化而变化；对于更换参考年的附近时段，如2000年，无论是从序列重构的稳定性角度，还是从环流变化的连贯性角度来说，更换参考年与否不应影响事件的性质。考虑全球变暖增温的极端情况，在这种趋势背景下，采用国标算法会导致一些困难：假设某一年份x处于更换标准值的年份(比如：2061年)的Nino3.4区的平均海温，2060年所采用的的标准值为2021—2050年的30年均值，而2061年则是2031—2060年的30年均值，假设2051—2060年间升温显著，此时，2060年、2061年所计算的两个监测值则会产生显著差异，而这两个年份的事件很有可能是连续的；此外，由于海温的上升，较大正强度的监测值可能对应较弱的暖事件，而较弱负强度的监测值则有可能对应强的冷事件(具体示意参见图1)。

为此，本文从分析的角度上，基于一种舍弃气候标准值的方法用以构建Nino海区海温指数。基于美国National Center for Atmospheric Research (NCAR)和University Corporation for Atmospheric Research (UCAR)的官方网站(https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni)所公布的Nino数据，本文选取ESRL/NOAA Nino 3.4(5°N～5°S, 170°～120°W), 1870年至今基于HadISST的数据[16]作为研究对象，对比两组序列的差异，以期能为上述问题的解决提供思路。

1 指数构建方法

如果气候是稳定少变的状态，在此情形下，气候标准值可以认为随时间近似不变；那么，气候标准值的选取将不影响距平的变化。随着研究的深入，全球气候变暖的研究虽有差异[17]，但关于变暖的趋势存在共识：Nino海区海温存在趋势性演变。在此基础上，仍采用参考年的处理手段就会导致上述问题的发生。

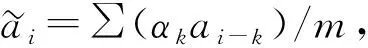
(1)

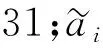
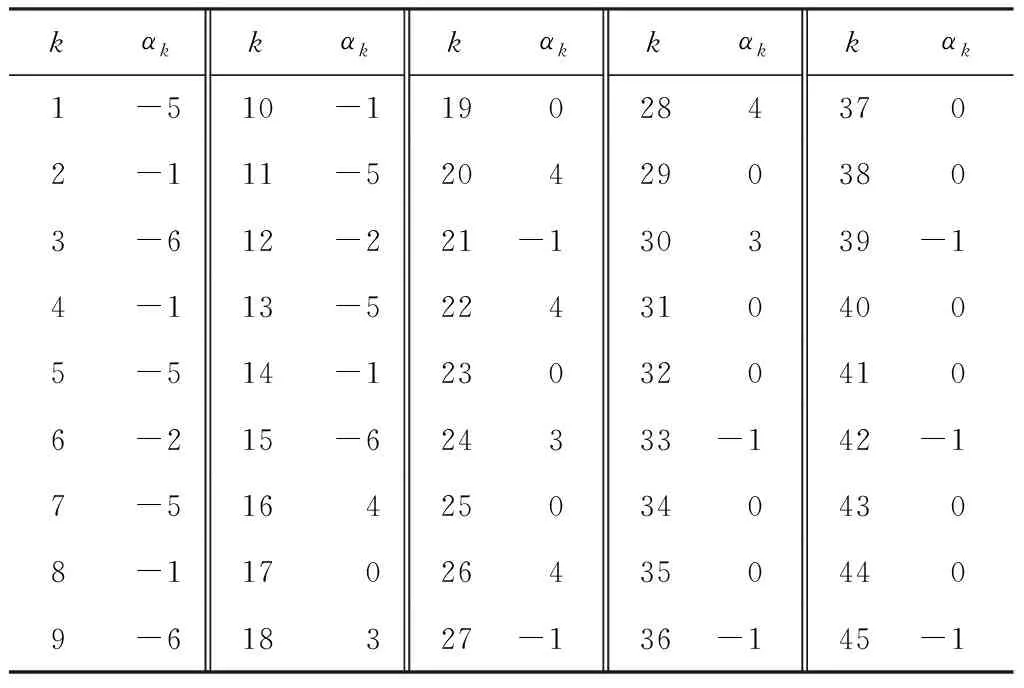
表2 式(1)中αk的取值

在下文中，对采用式(1)计算的异常序列简称式(1)序列；对采用国标计算的序列简称标准序列。值得一提的是本文方法计算的序列对趋势项没有国标算法那么敏感，本节将分析基于第1节中的数据(起止时间为1915年1月至2019年12月)由本文方法计算的序列及参考国标推荐算法计算的标准序列。在此之前，先给出一个具有增长趋势的理想信号(图1c)，序列对应事件同样设为1915年1月至2019年12月)采用两种方法计算异常，两组异常对比结果如图1。从图1中可以看出，采用国标算法在每次的标准值变更处会产生跳跃，且有杂波波纹(图1a)，而采用本文方法的则没有这一现象(图1b)，这一点从气候标准值的变化可以看出(图1d)。这种情形下，如果仍然采用国标推荐的算法，则极有可能较大的正强度对应弱的暖事件，而较弱的负强度对应强的冷事件。

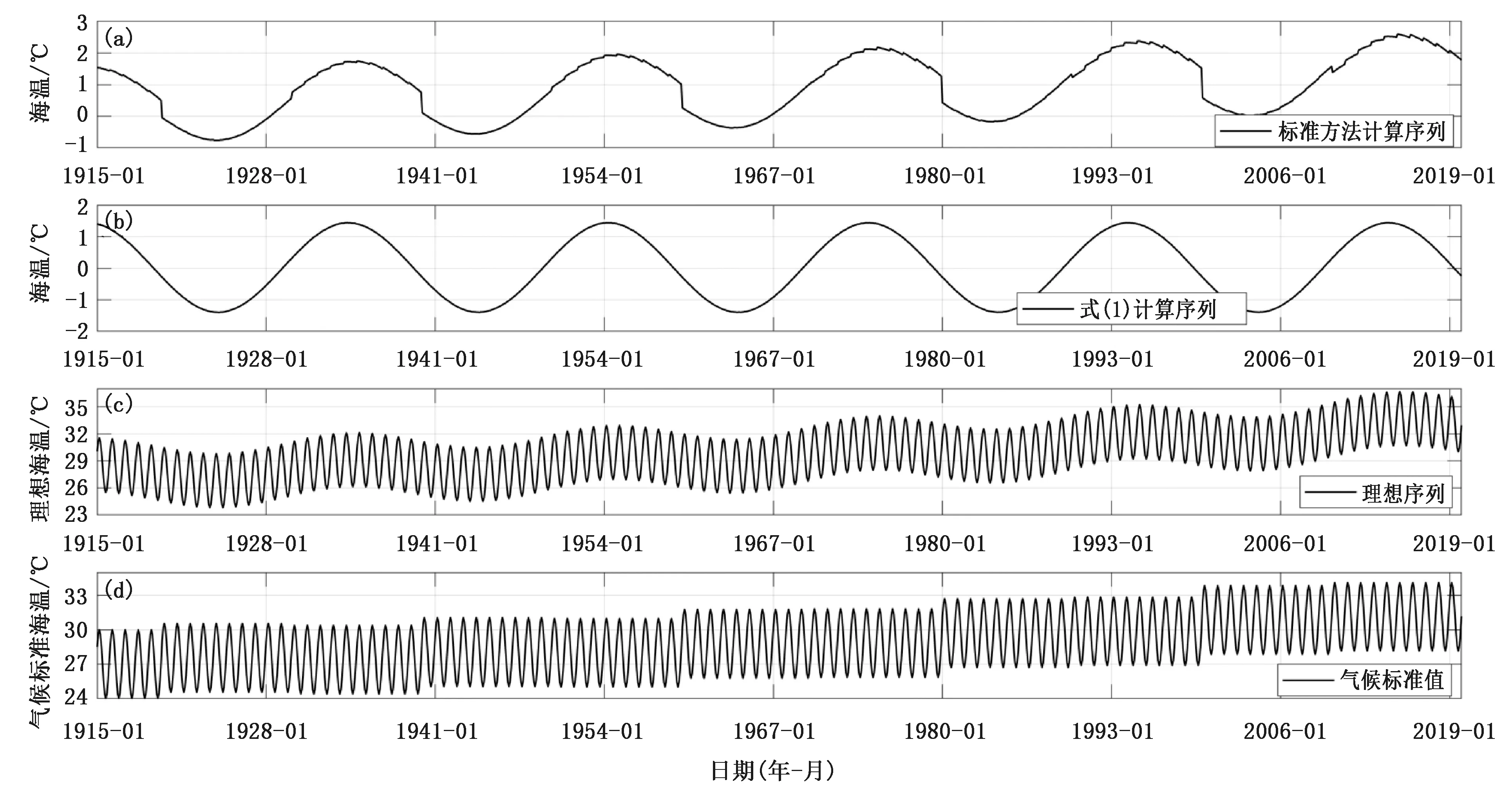
图1 基于国际标准方法计算的海温序列(a),本文方法计算的海温序列(b),理想海温序列(c),气候标准海温序列(d)

2 结果分析对比

基于本文方法和标准方法计算的两组序列在统计特征和走势上较为一致，但细节上仍存在较大出入。

对基于国家气候中心公布的数据生成的两组进行非参数差异性检验(Kruskal-Wallis方法)，检验结果表明两者不具备显著差异。两序列的相关系数为0.9；散点图和时间序列图如图2，对于ENSO强度大于2的6次事件以及强度小于负2的3次事件分布见表3。由于我们采用的数据与国家气候中心所采用的数据存在一定差异，所以计算的强度值也存在一定的差异，但极值所在月份基本一致：对于ENSO事件而言，较强的事件，本文方法和国标算法对于属性的判断基本一致，对于强弱的判断存在差异。

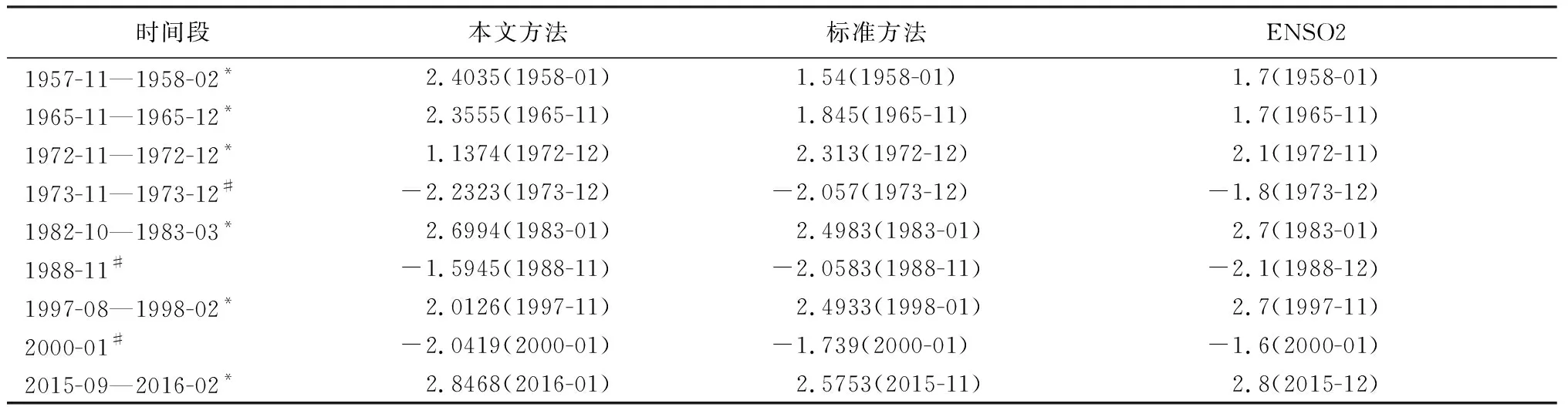
表3 ENSO强度绝对值大于2的9个时段极值分布及对应时间

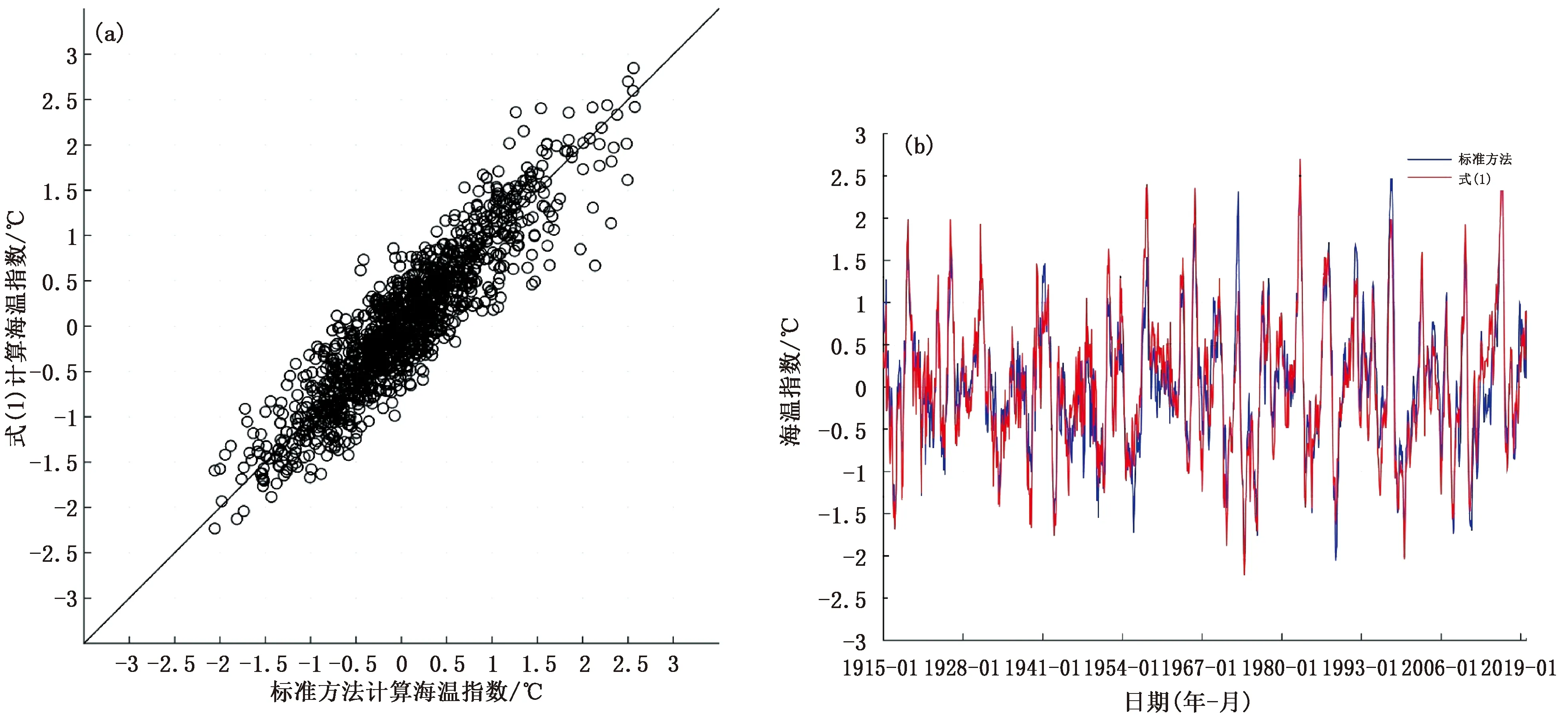
图2 基于标准方法和本文方法计算的海温指数对比：(a)散点图，(b)时间序列

无论从相关性、差异性角度，还是从值域或时间序列的走势来看，两个序列是高度相似的，但与标准序列相比较而言，本文方法计算的序列属于内秉的。为了更好地分析序列的属性，在此，对气候标准值、标准方案计算的序列和本文方法计算的序列做Mann-Kendall检验[18]。从检验结果(图3，图中标准序列是指采用国标推荐算法计算所得的异常，气候标准值是依据国标推荐的算法计算的30年均值，由于国标要求每10年更新一次，故而这个值是有趋势的)中可以看出，气候标准值存在显著上升时段(1920年前后至1970年前后)，1970年前后至2010年前后则是下降时段；其中1920年前后至1960年前后为明显上升时段，其间，标准序列部分存在明显下降时段，这一时段的重叠性意味着气候标准值的升降对标准序列的趋势变化存在影响。考虑到异常值的内秉属性，计算出的异常序列应当不具有明显的上升或下降时段，从这个角度来看，本文方法更具有参考价值。

图3 基于本文方法和标准方法计算的序列的Mann-Kendall检验

此外，两个序列的Morlet小波分析结果[18]表明：两个序列的全局功率谱基本一致，式(1)序列中的周期在10年附近的功率较标准序列偏弱；平均方差走势相似，值域一致；小波功率谱分布基本一致，但在一些细节上存在差异，主要差异集中在10年周期附近(图4)，而这一周期正好包含有10年的人工信号。

图4 基于标准方法计算序列的小波分析(a1,b1,c1,d1),基于本文方法计算序列的小波分析(黑白图)(a2,b2,c2,d2)

针对相关系数的定义，在此以西太副高的4个指数为例，分析基于本文方法的序列在实际应用中的一些特征。在第1节中，我们给出了一个理想带趋势序列计算异常的示例，在图1中，可以看出，如果对一个序列进行异常计算，其后所得的两个序列(式(1)序列和标准序列)将有着不同的特点，最为显著的是式(1)序列不含有趋势特征，这种不含趋势特征的序列在与未做异常处理的含趋势序列进行相关性的计算分析时，势必会因为不含趋势而使得两者的相关性较标准序列计算所得有所改变。依据相关系数ρ的计算公式(2)：

(2)

式中，xi(或者yi)代表第i时刻的采样值，带“-”变量表示采用周期类对应量的均值，假定x和y有相近的趋势特征，即，在接近的时段内，两者变化形势大致一致。如果，x与y呈现完全的线性关系，即，y=ax+b；那么，相关系数为1或者-1。做图2中式(1)序列和标准序列的差值(即，式(1)序列减标准序列所得的序列)与标准序列的散点图，则可以发现两者的分布较为离散，相关性较差(-0.31)。据此，可以认为式(1)序列s1与标准序列sb存在如下关系：

s1=sb+ε

(3)

对应相关系数ρ近似为：

(4)

以图2中的数据为例，式中，ε为均值是0，方差约为0.2的含趋势随机变量。而实际的回归方程为：s1=0.9543sb-0.0134。这也从侧面印证了两者有较好的替代关系。如果式(1)序列与其他要素的变化趋势相近，则计算所得的相关性较标准序列有所下降。将式(3)代入到序列与其他要素f相关性计算中，可以得到预估式：

(5)

总体来看，所得到新的相关系数的绝对值略有下降，依据式(3)的数据，估算下降的系数约为0.9，实际的相关系数可能比这还要再低一点。以西太副高的4个指数为例，黄小梅等[19]研究了副高指数初秋的年际变化趋势，发现面积指数和强度指数均有显著的线性增长趋势，其余两个没有显著趋势；薛峰等关于副高变化的研究也得有副高增强的结论[20]，依据这些结论和前面的分析，可以发现面积指数和强度指数与式(1)序列的相关性较标准序列要低，而其余两项则存在不确定性。在此，本文以国家气候中心公布的西北太平洋的副热带高压逐月的四个指数(http://cmdp.ncc-cma.net/Monitoring/cn_stp_wpshp.php?wpsh_elem=wpsh_GQ#wpsh)为例，计算的相关系数如表4。

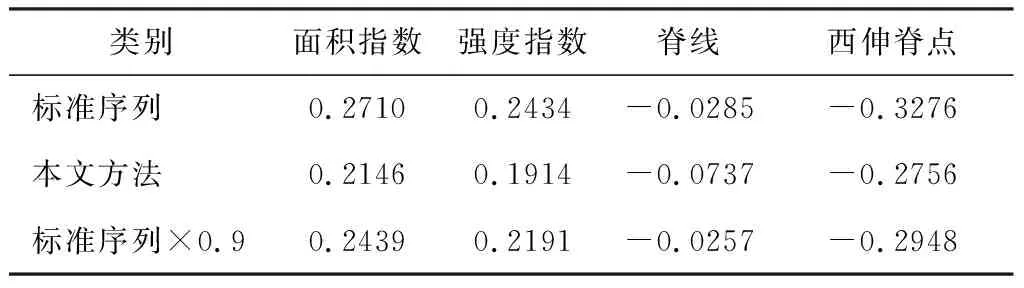
表4 副高指数与Nino3.4指数的相关性对比

对比表3的数据，可以发现，这些变量与式(1)序列的相关性基本可以接受，其与标准序列相关性的比比0.9略小，在0.8左右，其中，前两个的相关系数的绝对值是有所下降的，后两个则存在不确定性。综合而言，基于本文方法的指数序列基本与标准序列呈现大致相同的作用效果，但内秉性更好。

3 结论

本文基于一种趋势消除的方法构建了Nino海区海温指数的计算公式。该式从构造角度上看，舍弃了气候标准值这一参考量，通过小波分析、相关性分析、MK检验等系列分析检验方法，发现以本文方法为基础的指数基本保持了标准指数的所有特征；对具体变量而言，对应相关性较标准指数有所降低，其降低程度基本可估。此外，基于该方法计算的距平基本实现了异常属性的内秉特征，即，气候标准值的变动不会导致新指数中所判定的厄尔尼诺/拉尼娜事件属性的变化；也不会导致对应事件的强弱发生变化。此外，在做重构问题时，相关指数的重构具有较好的稳定性。