山区风力发电机组雷击风险评估方法

张 博, 孙 通, 聂家谊, 张 石, 夏 晖, 霍焕杰

(1.龙源(北京)风电工程技术有限公司,北京 100081; 2.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

0 引 言

随着对风能资源不断的开发,很多风电场布置在地形复杂的山区中。风机本身高耸的结构和山区中复杂的地形使风机极易遭受雷击,因此对山区风电场中的风力发电机进行合理、准确的雷击风险评估,为风机防雷装置提供理论依据是很有必要的。

早期对电力设备进行雷电防护评估时使用的是折线法[1],折线法通过对缩比模型进行试验得到防雷设备的保护范围,缺乏足够的理论分析。进一步深入研究后,电气几何模型[2]作为一种效果更佳的方法被提出来取代折线法。电气几何模型认为防雷设备的保护范围与雷电回击电流峰值相关,被实际应用于电力架空线的避雷设计等,但是电气几何模型对放电过程过度的简化,无法体现不同结构和高度的物体对附近电场带来的影响,在应用于高大或复杂形状的建筑物时,理论结果与观测结果差距较大。高大建筑物(如高塔、风机等),在遭受下行雷击时,往往会产生迎面先导,文献[3]提出一种自洽式先导发展模型(self-consistent leader inception and propagation model,SLIM),用来研究建筑物上行先导的始发情况,对下行梯级先导动态发展过程中何时导致上行先导始发进行了模拟;文献[4]将SLIM应用到风机上,计算叶片接闪器击距,为风机防雷系统设计提供了理论基础;文献[5]通过SLIM模型计算风机叶片不同位置的击距,得到叶片不同位置遭受雷击概率,解释了部分风机接闪器失效的原因;文献[6]基于之前的研究基础,利用SLIM模型对风机的雷击截收区域面积进行计算,结合地闪密度得到风机年均遭受雷击次数来表征风机的雷击风险。上述研究仅考虑风机本体对于雷击目标点附近电场的影响,未考虑风机所处地形结构与多风机间的屏蔽作用对风机雷击风险的影响[7]。

为了合理地对山区风电场中风力发电机组进行雷击风险评估,本文首先对风机及风机所处的地形结构,包括地形高度、地面倾角和风机所处位置3个方面进行建模;其次基于SLIM模型，计算风机处于不同地形结构下的风机雷击截收区域,并定量讨论回击电流与雷击截收区域的关系;最后考虑多风机屏蔽效应对风机雷击截收区域的影响,根据风机所在地的地闪密度和风机实际雷击截收面积,计算得到风力发电机组年均遭受雷击次数来表征风机的雷击风险。

1 雷击风险评估方法及计算

1.1 风机雷击风险评估方法

本文利用风机遭受年下行雷击次数来表征风机的雷击风险。

年下行雷击次数计算公式为:

N=DgS

(1)

其中:N为风机遭受的年下行雷击次数;Dg为风机所在地的地闪密度;S为风机雷击截收区域的对地投影面积。

风机所在地的地闪密度可以通过观测数据得到,也可以通过文献[1],利用所在地的雷暴日进行计算,即

Dg=0.04Td1.25

(2)

风机雷击截收区域示意图如图1所示,当发生下行负极性雷击时,梯级先导向下发展到一定区域内,风机叶片尖端等曲率半径较小的地方可以产生稳定发展的迎面上行正极性先导,最终下行梯级先导与迎面先导相连,雷电击中风机,将这个区域定义为风机的雷击截收区域。当梯级先导在向下发展过程中没有进入到风机的雷击截收区域时,雷最终会被大地或者其他物体所截收。

图1 风机雷击截收区域示意图

1.2 利用SLIM计算雷击截收区域流程

风机的雷击截收区域由雷云、下行梯级先导、大地和风机形成的空间电场决定。回击电流幅值决定了梯级先导通道总的电荷量,从而影响空间电场的大小。而地形结构的不同使风机附近的空间电场有不同程度的畸变,同时大地对雷电的截收距离也会发生改变。本文主要研究回击电流幅值和风机所处的地形结构与风机雷击截收区域的定量关系。

据观测数据显示,因为下行负极性雷电占雷电总数的90%以上[8],所以本文只对风机遭受下行负极性雷击的情况进行研究,根据雷电观测数据和仿真计算,设定风机高度最高的叶片尖端为风机的雷击目标点。风机雷击目标点正极性先导的始发是决定风机是否遭受雷击的重要因素。正极性先导发展需要经过初始流注起始、正先导起始和正先导连续发展3个重要环节[9],利用SLIM计算风机遭受雷击的流程如图2所示。

图2 利用SLIM计算风机遭受下行雷击流程

利用有限元法对雷云、梯级先导、风机和大地构成的空间电场进行求解,空间激励电场由雷云和下行梯级先导组成,本文采用文献[10]提出的电荷密度结构来对下行梯级先导通道内电荷分布进行建模,即大部分电荷集中在梯级先导头部,通道内距离梯级头部距离增加,在梯级头部内电荷量成指数衰减,而其余部分为线性衰减,与梯级通道电荷密度相关的表达式如下:

(3)

G(z0)=1-z0/L

(4)

J(z0)=0.3α+0.7G(z0)

(5)

(6)

其中:Ip为回击电流幅值;z0为梯级先导通道头部距离地面高度;L为梯级先导通道长度。梯级先导通道中的系数分别为:a0=1.476×10-5；a=4.857×10-5；b=3.909×10-6;c=0.522;d=3.730×10-3。

利用临界半径法的经验公式来判断风机上的雷击目标点是否有流注放电的产生,在小于临界半径的尖端附近，当电场强度达到3 MW/m时,风机雷击目标点发生流注放电。文献[11]建立的流注先导转换模型中认为当流注放电产生的电荷量大于1 μC时,则正先导始发。流注放电电荷量计算采用文献[9]提出的模拟电荷法,如图3所示。图3中:U0为雷击目标点与下行先导头部连线上的电位;U1为在ls处发生流注放电后流注区域的电位。

图3 流注起始时空间电位分布

发生流注放电产生的电荷量Q0为:

(7)

其中,kQ为几何因数,取3.5×10-11C/(V·m)。

先导起始后,先导头部会有二次流注产生,接着计算二次流注所转化形成先导的长度,当最终转化为先导的长度可以达到临界值2 m时,若满足稳定迎面上行先导起始的条件,则认为该梯级先导击中风机。若在计算过程中,先导长度的增量开始减小,则认为上行先导终止发展,梯级先导不会击中风机。

1.3 多风机屏蔽效应

当2台风力发电机组之间距离较近,雷击截收区域有交叠时,下行雷击的先导头部进入到交叠的雷击截收区域,雷击中2台风机的概率相同,因此2台风机的等效截收区域面积减少,这就是风机之间的屏蔽效应。

多数关于风机屏蔽效应的研究是对处于平原或海拔相等的风机进行雷击截收区域的计算,利用雷击截收区域的投影来计算多风机之间的屏蔽效应,而本文考虑地形结构对于风机雷击截收区域高度的影响,如图4所示。从图4可以看出,海拔相同的风机所处的地形结构对风机雷击截收区域的面积和高度都有影响,雷击截收区域较高的风机会降低附近雷击截收区域较低风机的雷击风险。

图4 未考虑地形结构和考虑地形结构的多风机屏蔽效应

2 计算过程及结果

2.1 计算对象

本文对云南雪邦山风电场中风力发电机进行雷击风险分析,云南雪邦山拥有66台1.5 MW的远景风机,塔筒高度为80 m,叶片长度为43.5 m。

风机所处地形结构从地形高度、地面倾角和风机所处位置3个方面进行描述,地形高度选取4、8 m 2种情况,地面倾角选取1°、3°、45°,风机所处位置选取了山顶和山坡2种情况进行建模。

2.2 计算过程及结果分析

(1) 设定回击电流幅值为25 kA,地形高度为40 m,地面倾角为10°,风机位于山顶,计算该情况下风机所对应的雷击截收区域。

建立计算模型如图5所示。按照上述计算过程，得到该条件下风机的雷击截收区域面积的对地投影如图6所示,形状近似圆形。雷击目标点的投影坐标是(-22,0),以X=-22为轴,轴的右侧地形结构比左侧对空间电场的畸变影响大,对应的雷击截收距离较远,平均截收区域半径为260 m。

图5 考虑风机所处地形结构的计算模型

图6 设定条件下计算得到的风机雷击截收区域投影面积

(2) 考虑回击电流幅值对于风机雷击截收区域的影响。保持地形高度为40 m,地面倾角为10°,风机位于山顶的条件不变,计算回击电流幅值为0～300 kA。

将计算得到的结果与IEC推荐的折线法、电气几何模型法计算结果进行对比,其中折线法与回击电流无关,仅与雷击目标物的高度有关,电气几何模型法参数设置可以参照经典公式，即

rs=6.72Ip0.8

(8)

折线法是根据实际观测数据和缩比实验得到的方法。3种方法对比结果如图7所示,从图7可以看出，本文的方法在发生频率概率较高的回击电流幅值下计算结果与折线法较为接近,而在发生频率概率较低的回击电流幅值下计算结果与电气几何模型法较为接近。

图7 3种方法计算得到的雷击截收区域投影面积

因为回击电流幅值服从概率分布,所以结合回击电流概率和不同电流下的雷击截收面积得到单台风机的等效雷击截收区域面积。将风机的等效雷击截收面积进行累加,与风机所在地的地闪密度相乘，最终得到该条件下风机遭受的年下行负极性雷击次数。

(3) 考虑地形结构对于雷击截收区域面积的影响。设定仿真条件地面倾角为10°,风机位于山顶,计算地形高度分别为40、80 m,回击电流幅值为0～300 kA,风机的雷击截收区域投影面积计算结果如图8所示。由图8可知，当地面倾角为10°时,80 m地形高度相较于40 m地形高度,在回击电流为25、45 kA时,风机雷击截收区域投影面积分别增加8%、16%。

图8 风机处于不同地形高度下的雷击截收区域投影面积

保持地形高度40 m不变,计算0°、30°、45° 地面倾角下的风机雷击截收区域投影面积,如图9所示。从图9可以看出，地形高度为40 m时,地面倾角30°、45°相较于10°时增加的比例为6.00%、6.82%。

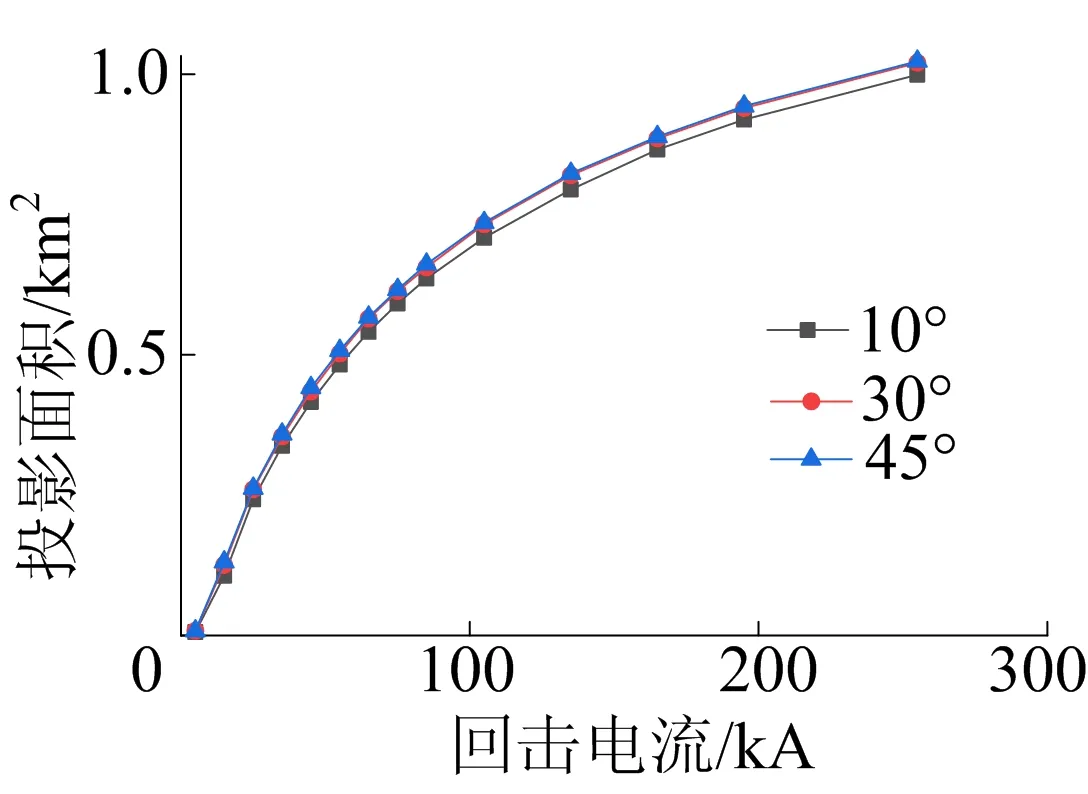
图9 不同地面倾角的雷击截收区域投影面积

结合雪邦山当地的地闪密度,统计不同地形高度和地面倾角下风机遭受年雷击次数,如图10所示。从图10可以看出，80 m的地形高度相较于40 m的地形高度,在地面倾角为10°、30°、45°下,风机遭受雷击次数增加的比例分别为17.3%、43.5%、47.4%。

图10 不同地形条件下风机遭受年下行负极性雷击次数

对风机位于山坡的情况进行仿真计算,建模如图11所示。由图11可知，地形高度为80 m,地面倾角为30°,叶片旋转角度为90°,风机高度分别设置为40、53 m,计算回击电流为0～300 kA下的风机雷击截收区域投影面积,结果见表1所列。风机位于山坡位置相较于风机位于40 m山顶位置,风机雷击风险增加了4%,影响较小。

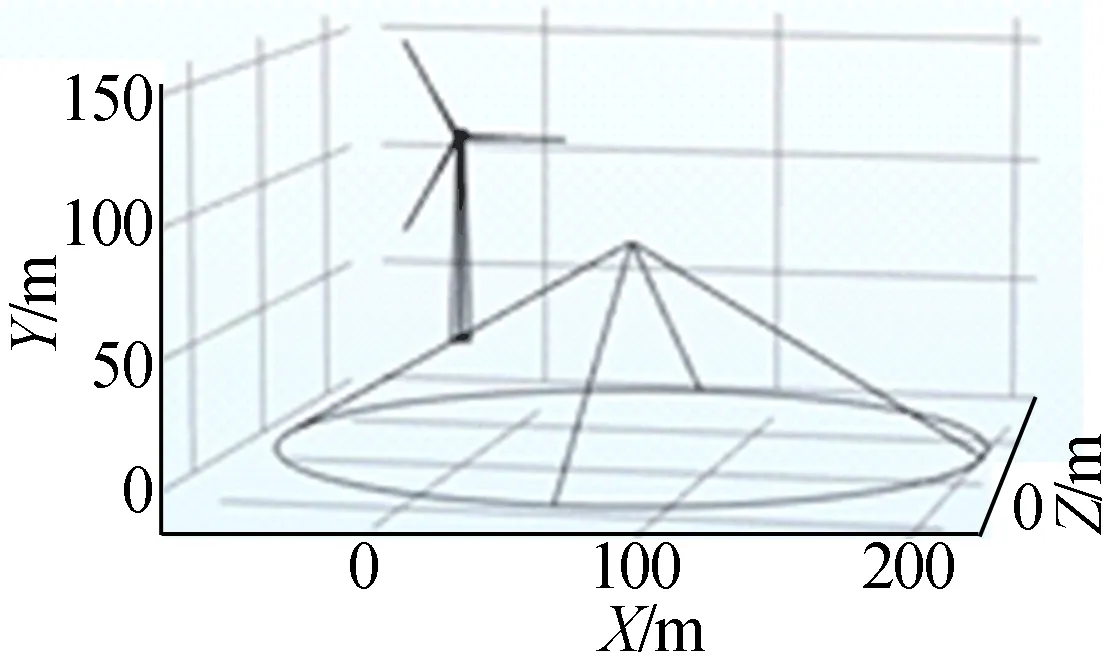
图11 风机位于山坡建模

表1 风机位于山坡不同位置时风机的雷击截收区域面积

当多台风机距离较近,风机雷击截收区域有交叠时,雷击截收区域的高度会在一定程度上影响多风机的屏蔽效应。风机雷击截收区域高度与地形结构的关系如图12所示。由图12可知，地形结构对风机雷击截收区域的高度和面积的影响相似,雷击截收区域高的风机会对雷击截收区域低的风机产生屏蔽作用。

图12 不同地面倾角下的雷击截收区域高度

3 讨 论

本文以云南雪邦山风电场为例,考虑山区中复杂地形结构和多风机屏蔽效应对风机雷击风险的影响,基于SLIM模型对风电场中风力发电机进行雷击风险评估。建立了地形高度为40、80 m,地面倾角为1°、3°、45°,风机位于山顶和山坡的雷击截收区域计算模型,计算得到不同地形结构与雷击截收区域的定量关系。

首先通过仿真得到回击电流对风机雷击截收区域的影响,风机雷击截收区域的面积随回击电流的增加而增加,呈对数增长；其次研究地形结构对于风机雷击截收区域的影响,地形结构中地形高度的变化对风机雷击截收区域的影响最大,地形高度变化一方面是改变风机所处的海拔,另一方面是地形高度的增加使得地形结构发生变化,从而使风机周围电势发生畸变。风机所处位置对于风机的雷击风险影响较小,部分地形较小的凸起或凹陷对于风机雷击截收区域的影响有限。

多风机雷击截收区域有交叠时,风机雷击风险的评估还需要考虑多风机的屏蔽效应。从部分地形结构与风机雷击截收区域高度的仿真结果可以看出,地形结构对风机雷击截收区域面积和高度的影响趋势基本相同,较高的地形高度和较大的地面倾角会使风机的雷击截收区域面积增加,使风机的雷击截收区域的高度变高。因此当2台不同地形结构的风机雷击截收区域有交叠时,2台风机的雷击风险均有所下降,而雷击截收区域面积较大的风机雷击风险下降得较小。

4 结 论

本文将SLIM模型应用到山区风力发电机组的雷击风险评估中,从地形高度、地面倾角和风机所处位置来描述风机所处的复杂地形,通过地形结构与风机雷击截收区域的定量关系和多风机间的屏蔽效应对风机雷击风险进行评估。

(1) 地形高度对风机雷击截收区域的影响程度大于地面倾角和风机所处位置。当风机位于山顶位置,地面倾角一定时,地形高度越高,风机的雷击风险也越高。80 m的地形高度相较于40 m的地形高度,在地面倾角为10°、30°、45°下,风机遭受雷击次数增加的比例分别为17.3%、43.5%、47.4%。

(2) 地形高度为40 m时,地面倾角30°、45°相较于10°时增加的比例为6.00%、6.82%。地形高度越高,地面倾角的变化对风机遭受雷击次数的影响变大。

(3) 山顶高度80 m,风机高度40 m,风机位于山坡位置相较于风机位于40 m山顶位置,风机雷击风险增加了4%,影响较小。

(4) 当多台风机的雷击截收区域有交叠时,雷击截收区域高度较高的风机会降低附近雷击截收区域较低风机的雷击风险,而雷击截收区域高度较高，风机的雷击风险变化较小。