改进鲸鱼算法及其在乘员约束系统中的应用

黄岳竹, 尹安东, 王笑乐, 谷先广,3

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009;2.安徽农业大学 工学院,安徽 合肥 230036; 3.太航常青汽车安全系统(苏州)股份有限公司,江苏 苏州 215100)

鲸鱼优化算法(whale optimization algorithm,WOA)是文献[1]提出的一种元启发式算法,具有初始参数少、原理简单且易于实现等优点。相较于粒子群算法(particle swarm optimization,PSO)[2]、灰狼优化算法(grey wolf optimizer,GWO)[3]、差分进化 (differential evolution,DE)[4]等经典算法,WOA具有更高的收敛精度和收敛速度,但在处理复杂的非线性问题时,WOA仍然可能因搜索力度不足而过早收敛于局部极值。

因此,研究人员采取了一些措施来改善算法性能。受PSO算法中惯性权重的启发,文献[5]利用非线性权重来加强算法的探索和开发,同时引入一种分段式非线性收敛因子来平衡全局搜索与局部开发;文献[6]利用自适应位置权重来改进算法的迭代策略,并通过自适应概率阈值来增强算法的灵活性;考虑到混沌映射的遍历性,文献[7]和文献[8]分别利用Logistic映射和Tent映射从不同角度来优化算法的搜索策略,混沌搜索能遵循其自身“规律”不重复地遍历所有状态,但在大空间、多变量的优化搜索上可能出现搜索不到最优解的情况;受混合算法的启发,文献[9]在WOA算法中嵌入模拟退火法,以加强算法的局部寻优能力;文献[10]基于寿命机制在WOA中引入了一个具有较强搜索能力的差分进化算子。实验结果证明算法融合有利于性能优化,甚至在某些问题上实现“1+1>2”的效果,但会增加计算复杂度。

综合来说,针对WOA的局限性,研究人员已经提出一些建设性的建议,但如何进一步提升算法的寻优速度和寻优精度仍需更深入的研究。为此,本文基于自适应权重、反向学习策略和相关性指标,提出一种改进的鲸鱼优化算法(modified whale optimization algorithm,MWOA)。通过4个基准测试函数对MWOA和WOA、基于非线性收敛因子和惯性权重的鲸鱼优化算法(whale optimization algorithm with nonlinear weight and convergence factor,WCLWOA)[5]、基于自适应参数及小生境技术的改进鲸鱼优化算法(whale optimization algorithm based on adaptive parameters and niche,APNWOA)[6]、DE、PSO、GWO算法的性能测试和比较,证明了MWOA算法的可行性和竞争性。最后为测试MWOA在实际工程中的应用价值,建立了正面100%刚性壁碰撞工况下某款汽车的乘员约束系统模型,利用PSO支持向量回归(PSO-support vector regression,PSO-SVR)模型技术[11]建立相应的近似模型,采用MWOA算法对乘员约束系统的性能进行优化,实现了乘员约束系统性能的提升。

1 鲸鱼优化算法

WOA衍生于自然界中座头鲸独特的捕食方法,捕食示意图如图1所示。在WOA中,各搜索代理(即鲸鱼)通过信息交流机制不断地获取猎物的信息并根据特定的捕食行为逐渐靠近猎物,最终找到猎物。鲸鱼的捕食行为包括包围猎物、攻击猎物、搜索猎物。

图1 座头鲸捕食示意图

(1) 包围猎物。将当前种群中的最优个体定义为猎物,其余搜索代理在其指引下逐渐聚拢收缩,形成包围猎物的趋势,其数学模型如下:

D=CXbest(t)-X(t)

(1)

X(t+1)=Xbest(t)-AD

(2)

其中:t为当前迭代次数;X为搜索代理的位置向量;Xbest为当前种群中最优个体的位置向量;A、C为系数。A、C可以表示为:

A=2ar-C

(3)

C=2r

(4)

其中:r为[0,1]之间的随机数;a为从2递减至0的控制参数,即

(5)

其中,T为最大迭代次数。

(2) 攻击猎物。在攻击阶段,搜索代理通过收缩包围机制和螺旋更新方式来更新种群位置,其数学模型如下:

D′=Xbest(t)-X(t)

(6)

X(t+1)=D′eblcos(2πl)+Xbest(t)

(7)

其中:b为常数,通常取b=1;l为[-1,1]之间的随机数。

(3) 搜索猎物。在搜索阶段,搜索代理在定义域内随机搜索猎物,其数学模型如下:

D″=CXr(t)-X(t)

(8)

X(t+1)=Xr(t)-AD″

(9)

其中,Xr为当前种群中随机个体的位置向量。

2 改进鲸鱼优化算法

针对WOA算法的局限性,本文提出一种改进的鲸鱼优化算法MWOA。该算法在WOA的基础上引入自适应权重策略和全局极值优化策略来改进算法性能。

2.1 自适应权重策略

WOA算法的寻优过程可分为探索和开发2个阶段。在探索阶段,搜索代理在整个搜索空间内寻找猎物,这个过程被称为全局搜索,此时全局搜索能力越强,种群多样性越好,算法早熟的风险也就越小。在开发阶段,搜索代理在全局最优个体的指引下迅速向其周围聚拢收缩,在局部区域内探索是否存在质量更高的个体,此时算法收敛速度加快,但搜索力度下降,算法可能过早收敛于局部极值。

受前人经验的启发,本文引入一种自适应权重系数w来增强算法的全局搜索能力与局部开发能力,自适应权重系数w的计算公式如下:

(10)

其中,wmax=1。利用权重系数w对随机个体Xr和全局最优个体Xbest进行扰动,改进后的迭代策略如下:

X(t+1)=(1-w)Xr(t)-AD″

(11)

X(t+1)=(1-w)Xbest(t)-AD

(12)

X(t+1)=D′eblcos(2πl)+(1-w)Xbest(t)

(13)

迭代前期扰动w较大,随机个体Xr和全局最优个体Xbest对种群的牵引力度较弱,搜索代理能够在更大区域内展开搜索,加强了算法的搜索力度。迭代后期扰动w逐渐趋近于0,算法局部寻优能力增强。

2.2 全局极值优化策略

在WOA算法中,全局极值起导向作用,指引种群向局部有利区域进行高效开发。换而言之,全局极值自身水平越高,其指引种群运动的方向就越正确,算法的寻优能力也就越强。因此本文通过反向学习策略和相关性指标对全局极值进行优化,帮助算法更加精确地锁定有利区域,提高收敛速度和收敛精度。

反向学习策略(opposition-based learning,OBL)是由文献[12]提出的一种计算智能方案,其核心思想是同时评估一个个体及其反向个体的优劣,并从中选出较好的个体进入下一代。通过反向学习策略计算出当前种群中全局极值的反向极值,计算公式如下:

Xr-best=bu+bl-Xbest

(14)

其中:Xbest为全局极值的位置向量;Xr-best为反向极值的位置向量;bu、bl分别为搜索空间的上、下限。

通常,研究者根据全局极值Xbest和反向极值Xr-best的适应度,择优选择适应度高的个体作为当前种群中的最优个体。而实际上,仅根据极值的适应度无法准确判定Xbest与Xr-best之间的优劣。这是由于Xr-best的适应度若优于Xbest,但Xr-best却远离种群,则意味着Xr-best所在区域可能只是一个局部最优区域,不具备开发价值。此时,若用适应度高的Xr-best代替Xbest,反而会影响算法的收敛精度。因此,本文提出了一种相关性指标来衡量Xbest和Xr-best与当前种群之间的相关程度,根据Xbest和Xr-best的适应度及其与种群间的相关度来更新全局极值。评价Xbest和Xr-best与种群间相关度的公式为:

(15)

其中:μ为当前种群中个体的均值;S为种群的协方差矩阵;S-1为协方差矩阵的逆矩阵。

MWOA算法流程如图2所示。

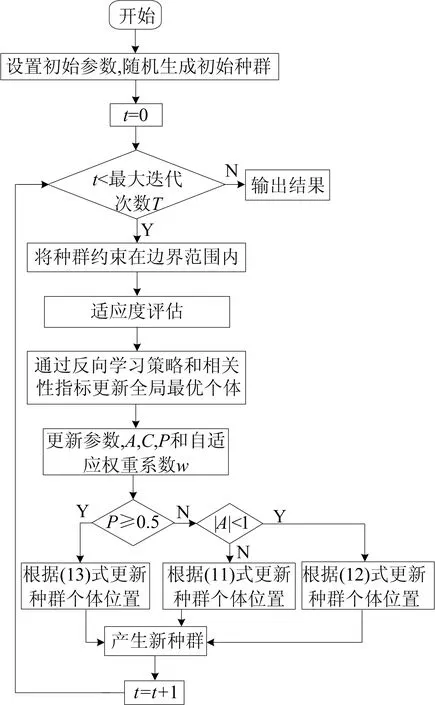
图2 MWOA算法流程

综上所述,MWOA算法融合了权重策略和全局极值优化策略来增强算法的全局搜索能力和局部开发能力。通过自适应权重系数动态调节算法的全局搜索与局部开发,增强算法的搜索能力。通过OBL和相关性指标来优化全局最优个体,提高算法的开发效率。

3 函数测试与结果分析

为了验证MWOA的收敛速度和收敛精度,本文选用4个基准测试函数来测试算法性能,并将其与WOA、APNWOA、WCLWOA、DE、PSO、GWO算法性能进行对比分析。

基准测试函数的具体信息见表1所列。仿真测试在Matlab编程软件中实现。

表1 基准测试函数

各算法的参数设置见表2所列。其中,参数N、T、v、wmax、wmin、c1、c2、F0、pc分别表示种群规模、最大迭代次数、维度、最大权重系数、最小权重系数、个体学习因子、社会学习因子、变异系数、交叉概率。

表2 算法参数设置

算法最大迭代次数为500次,为保证优化结果的可靠性,每种算法独立运行30次,取优化结果的均值、标准差以及平均计算时间,结果见表3所列。其中:均值表示算法的收敛精度;标准差表示算法的稳定性;计算时间表示算法收敛到最优解所需的计算时间。

由表3可知:就均值和标准差而言,MWOA算法在函数F1、F2、F4上均获得了理论最优值,其精度和稳定性明显优于PSO、DE、GWO、WOA算法,并且与APNWOA和WCLWOA算法精度一致；在函数F3中,7种算法都只获得了次优解,其中MWOA算法收敛精度最高且最稳定。

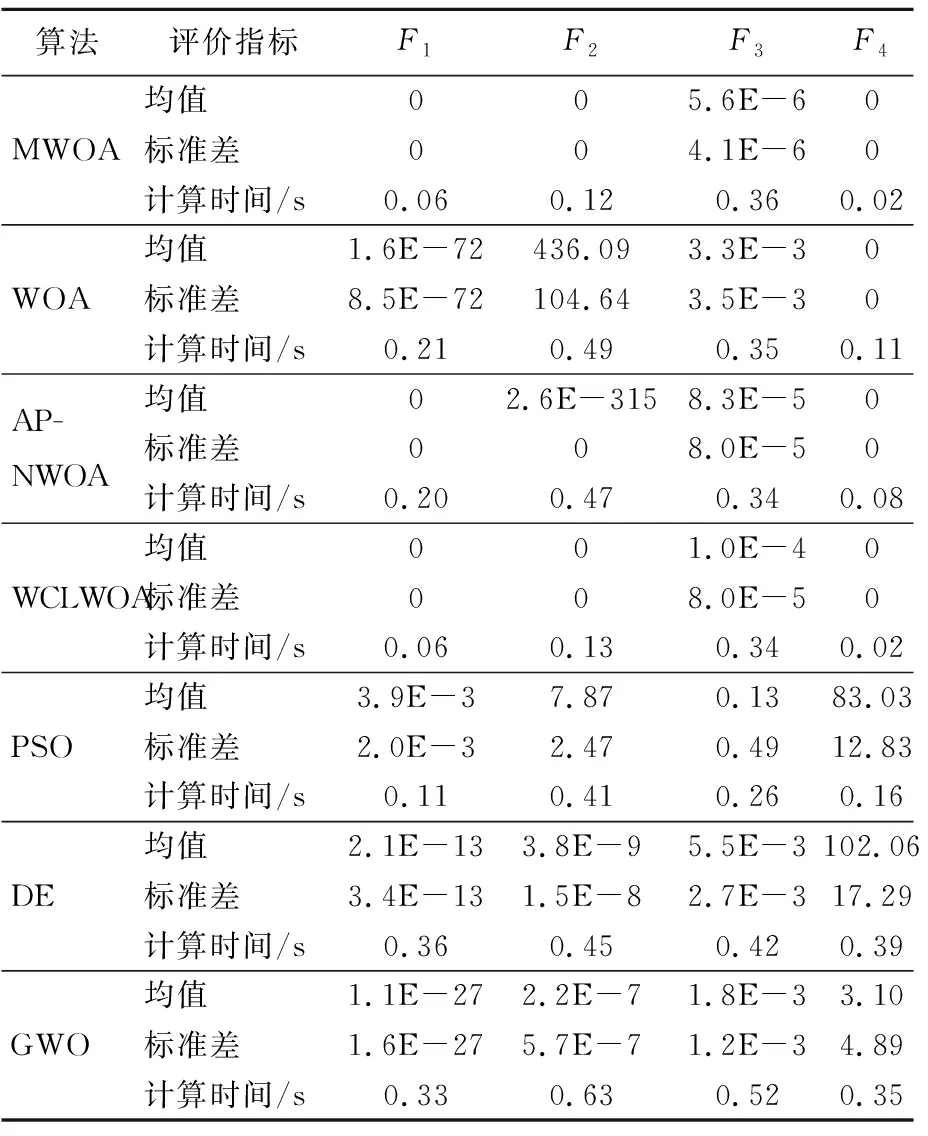
表3 优化结果

从表3的计算时间上来看,PSO算法的计算速度快于WOA、DE、GWO算法但计算精度较低;MWOA算法在函数F1、F2、F4中计算速度最快且精度最高，虽然在函数F3中,该算法计算速度略有不足，但同样获得了最高的精度。

MWOA、WOA、APNWOA、WCLWOA算法的收敛曲线如图3所示,该曲线直观展示了各算法收敛至最终解时所需的迭代次数。

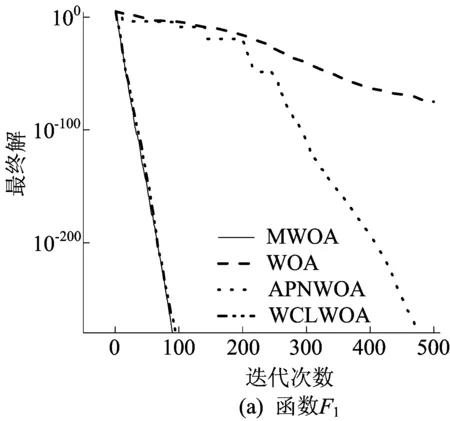
由图3可知,MWOA算法的收敛速度最快,WCLWOA算法次之,WOA算法最慢。

综合来说,相较于WOA算法，本文提出的MWOA算法的收敛速度和收敛精度有明显改善,并且相较于APNWOA、WCLWOA算法以及其他典型的优化算法,MWOA算法也具有一定的优势。

4 MWOA算法的应用

为了验证MWOA算法在实际工程中的应用价值,采用提出的算法优化正面100%碰撞下乘员约束系统的性能,具体内容如下。

4.1 乘员约束系统建立

本文根据C-NCAP(China-New Car Assess-ment Program)碰撞测试评价体系,利用MADYMO仿真软件建立了正面100%刚性壁碰撞工况下的乘员约束系统模型,如图4所示。

图4 乘员约束系统模型

乘员约束系统模型由驾驶室模型、约束系统模型和假人模型3个部分组成。驾驶室模型包括座椅、仪表板、防火墙、踏板、转向系统等;约束系统模型包括安全带和安全气囊;假人模型采用Hybridr Ⅲ50百分位男性假人。

此外,为了确保模型能够准确反映真实的运动状态,定义车体、约束系统与假人之间的接触关系,并对整体模型施加垂直向下的重力场和对假人模型施加沿着运动方向的加速度场。

4.2 优化问题定义

4.2.1 设计变量

乘员约束系统旨在保护乘客在意外事故中不会遭受过大的伤害,因此本文选择对乘员损伤影响最大的5个关键参数作为设计变量,即限力器限力等级X1、预紧器预紧时间X2、排气孔直径X3、充气质量流率比例X4、气囊体积X5。

系统设计变量的初值以及取值范围见表4所列。

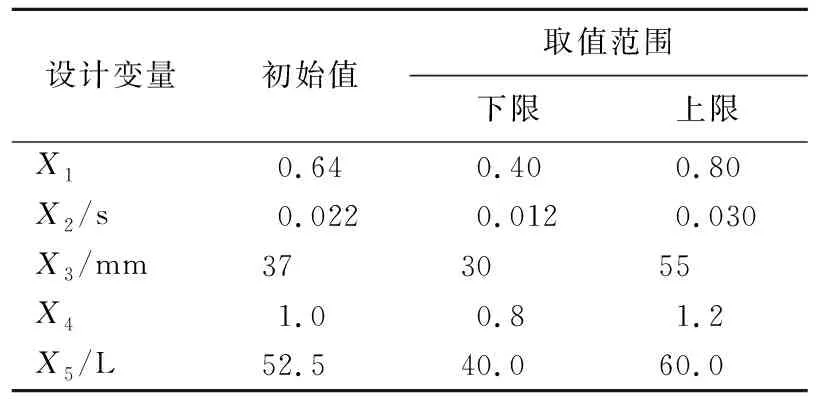
表4 设计变量初值和取值范围

4.2.2 目标和约束

以加权伤害指标WIC作为优化目标,以胸部压缩量Ccomp、左右大腿轴向力FFCL和FFCR、头部伤害指标HIC36、胸部3 ms加速度C3 ms作为约束,各响应的初始值和目标见表5所列。

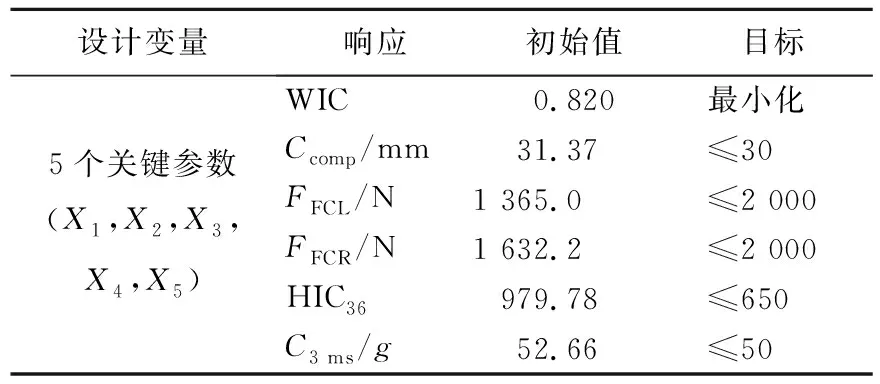
表5 响应初值和目标

由表5可知,在初始设计中,除了左右大腿轴向力满足要求之外,胸部压缩量、头部伤害指标和胸部3 ms加速度均不满足要求,乘员的头部和胸部受到了较大的伤害。

因此需要进一步优化乘员约束系统的性能来降低对乘员的伤害。

4.3 近似模型构建

在优化过程中,往往需要经历成千上万次评估才可能获得令人满意的结果,如果直接利用复杂的有限元模型进行响应预测,那么将会花费巨大的时间成本,影响优化效率。因此,利用高精度的近似模型取代有限元模型来拟合变量与响应之间的关系，是优化设计中不可或缺的一步。

采用试验设计在变量的设计空间内生成140组均匀分布的样本点,并通过MADYMO软件对乘员约束系统模型进行仿真分析,计算出每组变量样本点对应的输出响应。其中,120组样本点组成训练样本集,20组样本点组成测试样本集。利用训练样本集中变量与响应之间的关系构建PSO-SVR模型,利用测试样本集验证模型精度。精度指标为确定系数R2和最大相对误差ERmax,模型精度结果见表6所列。

从表6可以看出,每个响应对应的PSO-SVR模型的精度指标均满足R2≥0.9、ERmax≤5%,模型精度满足要求,可用于后续优化。

表6 模型精度

4.4 基于MWOA算法的乘员约束系统优化

乘员约束系统优化问题的数学表达式如下所示:

min WIC;

s.t.Ccomp≤30 mm,

FFCL≤2 000 N,

FFCR≤2 000 N,

HIC36≤650,

C3 ms≤50g，

(16)

采用MWOA算法调用建立的PSO-SVR模型进行优化,优化结果见表7所列。

由表7可知:经MWOA算法优化后,约束指标Ccomp、HIC36、C3 ms有了明显的改善,满足约束要求;右大腿轴向力FFCR略有增加,但仍处于合理范围内;优化目标WIC降低了45.3%,优化效果显著。

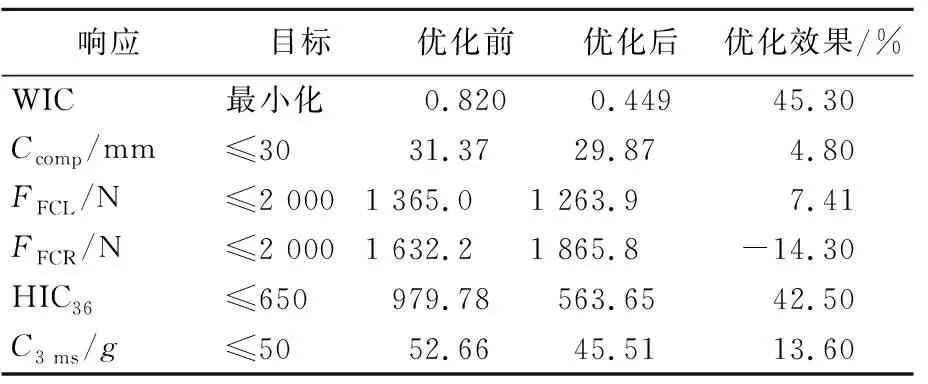
表7 正面碰撞工况下的优化结果

设计变量的优化结果见表8所列.

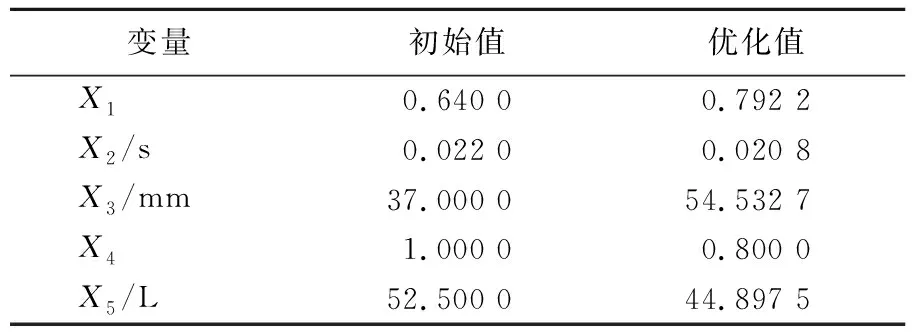
表8 设计变量优化结果

5 结 论

本文针对WOA早熟收敛的问题,提出了一种新颖的MWOA算法。该算法利用自适应权重系数的灵活性来增强算法的搜索能力,并通过反向策略和相关性指标来改进全局极值,指引种群向更有优势的区域进行高效开发。4个基准测试函数的实验结果证明，该算法具有较好的收敛速度和收敛精度。

最后,联合MWOA算法和PSO-SVR模型优化乘员约束系统,使乘员的加权伤害指标降低了45.3%。