虚幻引擎中多源地理数据坐标整合研究与应用

王 刚, 马 锦

(重庆市勘测院，重庆 401120)

0 引言

游戏开发引擎在三维场景可视化表达方面表现突出，已被应用于建筑、影视和三维地理信息等多个领域。在三维地理信息的可视化过程中，如何整合不同参考系下的多源地理数据一直是一个难题。地理数据参考有大地坐标系、投影坐标系、地理坐标系和工程坐标系等多种坐标系统，不同坐标参考下数据的位置、形状存在明显差异。传统的地理信息系统(GIS)通常支持常用的坐标转换功能，以实现两个或多个参考系下的数据在可视化和叠加分析等操作中的位置统一。游戏开发引擎早期的建设过程中并没有考虑多参考系地理数据的整合问题，因此在将其用于三维GIS的建设时，存在坐标难以统一的问题。本研究以虚幻引擎4(Unreal Engine 4，UE4)为例，分析不同坐标系下数据在UE4中存在的问题，针对存在的问题研究解决方法并应用实践。

虚幻引擎是EpicGames公司开发的三维场景创作平台，UE4是其第四代产品，目前已更新至4.27，在不久的将来第五代虚幻引擎也将正式推出。UE4具有强大的三维可视化、虚拟仿真、场景交互等功能，不仅是应用最广泛的游戏创作平台，还被用于影视、建筑、汽车、GIS等领域。在跨平台方面，UE4可以支持Windows、IOS、Android、Xbox等多种平台，为不同设备不同场景的应用提供了强大的支撑[1]。此外，UE4的开发具有蓝图和C++两种模式，其官网提供了大量的开发教程，其开发方式简单，门槛低，深受广大3D创作者的青睐。

在三维地理信息场景的建设中，三维地理数据通过转为FBX和OBJ等中间格式导入UE4引擎中，利用UE4的大气模拟、光影效果、粒子效果以及材质系统等功能，可以逼真地模拟真实地理场景，同时利用其交互功能，可以在时间和空间上对逼真的地理场景进行漫游。

1 UE4中坐标整合存在的问题

UE4自身的坐标系统为空间直角坐标系，而三维地理数据的坐标系有空间直角坐标系、投影坐标系、地理坐标系和工程坐标系，将不同坐标系的数据整合到UE4平台中主要存在坐标轴方向不统一、形变不同、参考面不统一以及定位精度不够等方面的问题。

1.1 坐标轴方向不统一

UE4中的坐标系为左手系，而三维地理数据的坐标系多数为右手系，左手系与右手系的差异表现在z轴方向的不同，如图1所示。

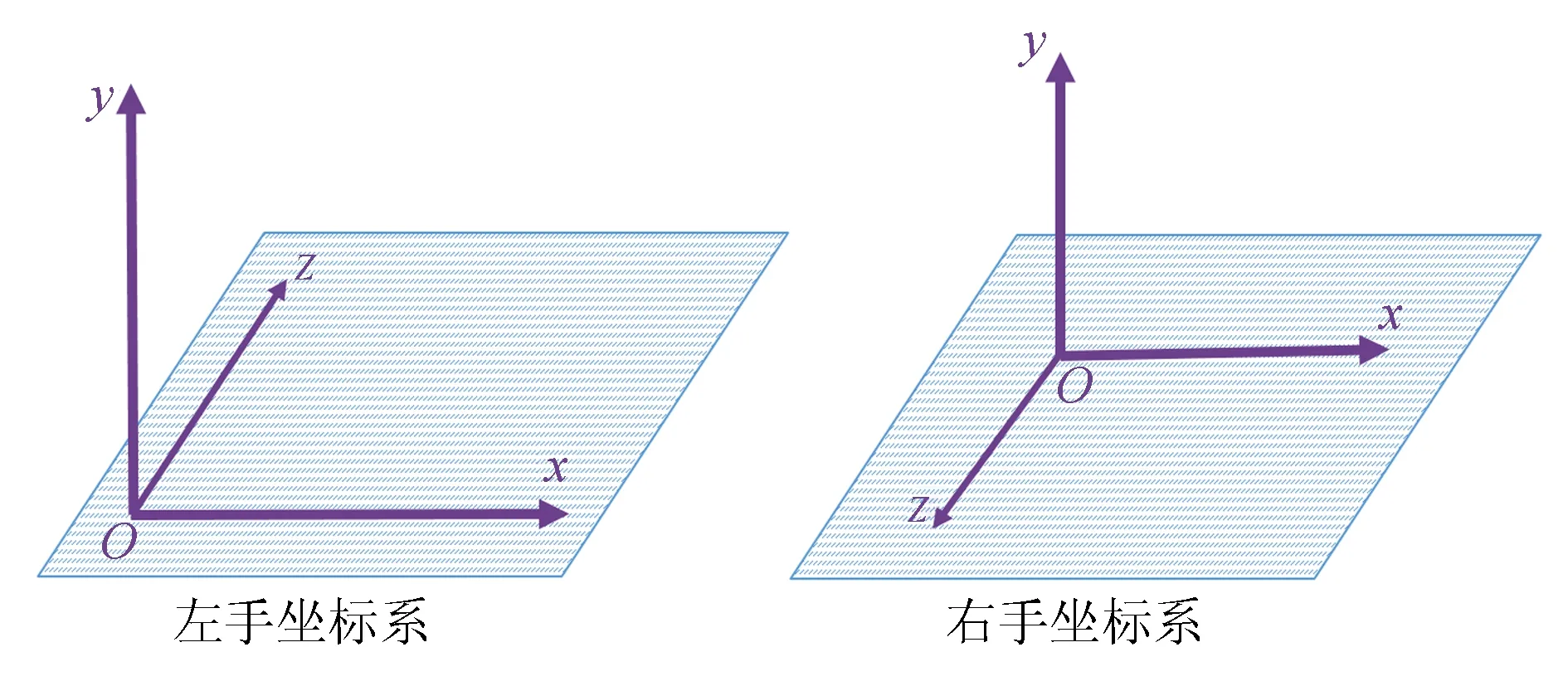
图1 左手坐标系与右手坐标系差异示意图

由于坐标轴方向的不同，右手空间直角坐标系导入后，保持z轴向上，则y轴的方向会被翻转，原本的正方向会变成负方向，发生翻转的地物与实际地物呈镜像显示，显示情况如图2所示。

图2 数据因坐标轴方向的不同而发生翻转

坐标轴方向的不同给地理场景的可视化、位置计算、方向判断、感知信息接入等环节造成了一定的影响，在应用过程中需要进行专门处理。

1.2 形变不同

地球表面是一个不规则的球面，将不规则的球面通过数学变换展开到平面上的过程称为地图投影，不论选择何种投影方式，投影过程中都会发生形变。以高斯-克吕格投影为例，其示意图如图3所示。

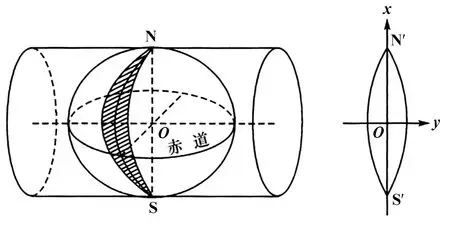
图3 高斯-克吕格投影示意图

高斯-克吕格投影是一种横轴等角切圆柱投影，分为3°分带和6°分带两种。无论是3°分带还是6°分带，其投影结果都有以下4个特点[2]：(1)中央经线上无变形；(2)除中央经线外其他地方均有变形，且变形长度均大于1(即被拉伸)；(3)距离中央经线越远的地方，变形越大；(4)距离赤道越远的地方，变形越小。

根据以上特点可知，投影坐标系下不同区域的地物形变方向和形变程度均不相同，不同的投影系下的数据受参考椭球、投影方式以及中央经线等影响，相同区域的地物变形也会不同。将不同投影坐标系下的三维地理数据导入UE4中，其位置会存在差异。

1.3 参考面不同

地理空间数据的高程和方向因坐标系的不同而存在差异，其中空间直角坐标系与一般的平面直角坐标系存在本质的不同。

以CGCS2000椭球体空间直角坐标系为例，原点和轴向的定义是：原点在地球的质量中心；z轴指向IERS参考极(IRP)方向；x轴为IERS参考子午面(IRM)与通过原点且同z轴正交的赤道面的交线；y轴与z、x轴构成右手正交坐标系。示意图如图4所示。

空间直角坐标系是三维地理数据常用的参考系，其优势可以将整个地球表面、地下以及空中用一个坐标系表达，在这个坐标系下地物几乎不存在变形，地物的形状、相对位置精确。利用空间直角坐标系进行数据的组织是地理空间数据“上球”的重要方式。

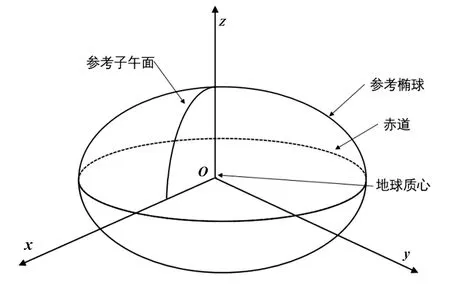
图4 空间直角坐标系示意图

投影坐标系与工程坐标系的高程通常以似大地水准面为准，方向为垂直向上，而在空间直角坐标系中，地物是垂直于椭球面向上的，不同位置的地物其朝向不同。参考系为空间直角坐标系的地理数据导入UE4中，很难与平面直角坐标系数据进行配准，给数据的叠加分析和可视化造成了困难。

1.4 定位精度的限制

虚幻引擎最初是为了游戏开发而打造的，没有将地理数据的范围大、精度要求高的特点考虑其中。在UE4编辑器中，数据类型只有单精度(float)而没有双精度(double)类型。众所周知，单精度数据类型的比特数为32，有效数字为6～7位，且UE4编辑器中的距离单位通常为厘米，由此可以推算，当精度为厘米级时，UE4中可精确表示的最大坐标范围在10～100 km之间，定位精度要求更高的数据则可表示的范围更小。在地理场景的搭建中，数据范围往往比较大，远远超过了单精度浮点型数据类型的精度，float数据类型无法满足UE4中大场景的定位需求，从而影响多源地理数据的叠加。

2 解决方法

根据以上分析，虚幻引擎加载地理三维数据过程中存在坐标轴方向不一致、参考面不一致、形变不均匀以及数据精度不满足等问题，本文对这些问题结合实际应用环境，提出了相应的解决方案。

2.1 坐标轴方向翻转

在地理三维模型数据导入UE4过程中，因坐标轴方向不同引起的y坐标值相反问题可以从数据导入引擎后和数据导入引擎前两个环节进行解决。

当数据导入引擎内部后，可以在引擎内部进行翻转，使其y轴方向上的值为原来的相反数。UE4提供了简单易用的位置变换接口，用户只需要在编辑器中对应的位置输入变换值即可。如图5所示，选择要变换的模型数据，在图中的位置输入数值“-1”，模型数据即会发生翻转。

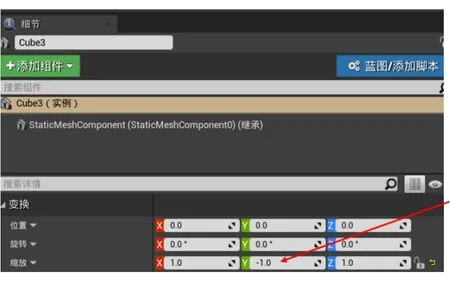
图5 UE4编辑器中利用位置变换对y轴进行翻转

除了在编辑器中进行变换，还可以对导入前的数据进行预处理。在预处理过程中无需对模型的所有顶点坐标进行更改，只需要给模型加一个变换矩阵即可。坐标变换计算如公式(1)。

(1)

式中：P′为变换后的左手坐标系下的点坐标；Sy为由于翻转y轴的变换矩阵；P为右手系下的点坐标。

通过以上方法进行坐标轴的翻转实现右手系和左手系的转换可以使地理场景在UE4中正常显示。

2.2 减小相对形变

相对形变是由于坐标参考系不统一导致的，减小或消除相对形变的重要手段是统一坐标参考系，该过程需要将不同坐标系下的数据转换到同一坐标系下。坐标转换通常情况下可以分为已知参考系的坐标转换和未知参考系的坐标转换，未知参考系的坐标转换需要通过控制点进行转换参数的拟合，通常分为平面四参数和三维七参数两种。

(1)已知参考系坐标转换。已知参考系的坐标转换通过借助数学函数库进行高斯反算、椭球变换和坐标投影等过程完成。例如将西安80坐标系3度分带105°带下的数据转换到CGCS2000坐标系3度分带105°带下的步骤如图6所示。

图6 已知参考系间的坐标变换

(2)四参数转换。平面四参数转换方式利用已知同名点进行拟合获得最佳的转换参数，利用公式(2)进行转换[3]。

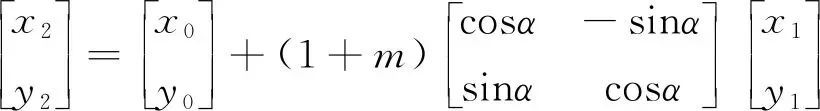
(2)

式中：x0,y0为平移参数；α为旋转参数；1+m为尺度参数；x2,y2为输出坐标系下的平面直角坐标；x1,y1为原坐标系下平面直角坐标。

(3)七参数转换。与四参数转换原理相似，七参数转换是用于三维坐标间的转换[4]，相对四参数多了1个平移参数和2个旋转参数，转换公式如(3)所示。

(3)

式中包括三个平移参数，三个旋转参数和一个尺度因子。其中x，y，z表示转换后的坐标； Δx，Δy，Δz为平移参数；εx,εy,εz为旋转参数；m为尺度参数；x′,y′，z′为原坐标系下的三维坐标。

2.3 统一参考面的方法

空间直角坐标系下的地物在地表上呈现一个球面，具有一定的曲率，将其导入UE4后与平面数据无法叠加，对此可以预先将空间直角坐标系数据转换到平面坐标系，可以利用地图投影的方式进行[5]。当工程范围不大时，可以通过矩阵变换将曲面数据与平面数据尽可能重合，以减小差异。如图7所示是地表曲面与平面叠加的高差与位置分析。

如图7所示，当范围距离D为1 km时，高差ΔH≈0.0784 m。在UE4中将平面系三维数据与空间直角坐标系球面数据进行叠加效果如图8所示。当D超过一定范围时，球面坐标系数据和平面坐标系数据高差会明显增加，球面数据会被平面数据遮挡。同时，随着D的增加，地物在平面上的距离也会发生明显变化。对于此方法的适用范围，可以根据工程的精度要求进行确定。

图7 曲面与平面叠加高差与位置关系示意图

图8 球面坐标系数据与平面坐标系数据(底板数据)叠加效果

2.4 提高UE4坐标表达精度的方法

为了满足UE4中单精度数值存储类型的数据精确性，工程中可将绝对坐标的值拆分为两部分，其中统一的、大数值的偏移量保留于数据外部，而文件中存储的则是减去一个较大数值后的数字，可以为-99 999.9～99 999.9之间，如此可以保证1 mm的定位精度。例如投影平面坐标值为(65 312 345.6,327 512 345.6)(单位cm)则可以表示为(653×105+12 345.6，3 275×105+12 345.6)。

3 应用实践

利用以上的分析与研究，本文进行了虚幻引擎加载多源地理数据的实验。实验使用数据有CGCS2000投影坐标系下的倾斜摄影实景数据、WGS84空间直角坐标系下的地形数据以及地方独立坐标系下的手工模型数据。

实验将倾斜摄影实景数据通过坐标值拆分的形式进行了坐标值的减小，从而避免其导入UE4后丢失精度，利用四参数的形式将手工模型与倾斜摄影实景数据所匹配，最后利用七参数转换的方式将地形数据与前者数据进行匹配。最终结果显示，三者数据位置相对准确，可以满足三维地理场景的视觉要求，显示效果如图9所示。

图9 多源三维数据整合效果

4 结束语

本文从虚幻引擎加载多源地理数据存在的坐标不统一的问题出发，分析了各参考系下数据的特点，提出了解决坐标轴翻转、数据变形、参考面不统一以及数据精度不够的方法，可为虚幻引擎加载多源地理数据提供参考。