关于高层建筑空旷大厅穿层柱计算长度系数的问题研究

王成

0 引言

在穿层柱的设计中强度和稳定性验算往往起了控制作用，其中强度包含正截面抗弯强度、斜截面抗剪强度；而穿层柱的破坏形式主要是由穿层柱的失稳破坏导致整体结构的破坏，因此在设计中穿层柱的稳定性验算问题就显现得尤为突出；而《混凝土结构设计规范》GB50010-2010（2015 版）6.2.20 条中只是给出了一般框架结构的计算长度系数，并未给出关于穿层柱的计算长度系数，导致在设计阶段由于对穿层柱计算长度系数的取值不同，造成设计的不合理；另《超限高层建筑工程抗震设防专项审查技术要点》（建质〔2015〕67 号）超限审查文件中第七条第7 项中局部穿层柱计算属于局部不规则项，因此关于如何确定穿层柱的计算长度系数在结构设计中成了首要解决问题。本文通过实际案例简单介绍如何利用屈曲分析确定穿层柱的计算长度系数，其结论对穿层柱的设计具有一定的指导性意义。

1 穿层柱计算长度系数的确定方法

关于穿层柱的计算长度系数的确定一般主要采用线弹性屈曲分析来实现，目前对整体结构或局部构件进行屈曲分析主要有整体模型法、独立构件法（不推荐）以及实体有限元法等，然后通过欧拉公式反推得到穿层柱的计算长度系数，公式如下：

式中：P—屈曲临界荷载；—构件几何长度；—弹性模量；—截面惯性矩；—构件计算长度系数。

2 通过整体屈曲分析得到穿层柱的计算长度系数

采用整体模型进行屈曲分析可以得到较为直观的屈曲模态，直接看到结构整体的屈曲变形，并通过甄别从较多屈曲模态中得到所分析构件的屈曲模态，一般情况下屈曲荷载选取荷载标准值（1.0 恒+1.0 活）进行计算，得到穿层柱发生失稳时所对应的屈曲临界荷载P，并根据欧拉公式反推得出穿层柱的计算长度系数。

整体模型进行屈曲分析根据加载模式的不同，其分析结果略有差异。

2.1 采用荷载标准值进行加载（1.0 恒+1.0 活）

这种加载模式的优点是与结构实际受荷情况相吻合。缺点是无法通过屈曲分析直接获取穿层柱的临界荷载，分析时需要计算比较多的模态，并通过甄别得到所分析构杆件的屈曲模态，以得到临界荷载系数。

2.2 选取相应的杆件，并在该柱柱顶施加单位集中力

这种加载模式的优点是可以根据屈曲分析直接得到穿层柱的临界荷载系数，直接计算得到临界荷载。缺点是不能反应结构整体受荷状态。

3 通过独立杆件模型进行屈曲分析得到穿层柱的计算长度系数

考虑到实际结构的复杂性，直接通过整体模型计算得到穿层柱的计算长度系数，计算量比较大，结果也具有一定的离散型，因而在上述理论的基础上，引入一种简单的计算方法，即独立杆件法，具体操作如下：

（1）取独立穿层柱作为分析模型。

（2）确定穿层柱上下节点的三个平动和三个转动弹性约束刚度系数。

约束刚度系数的确定：

①取整体模型，删除要求计算的穿层柱；

②在穿层柱约束节点处分别施加矢量方向沿整体的单位力和单位力偶，从而分别得到单位力和单位力偶下的平动位移和转角，其倒数即为该处其他杆件对柱的约束刚度系数。

（3）建立穿层柱及相应弹簧约束刚度系数的稳定分析模型。

（4）通过计算得出穿层柱的屈曲模态及对应的临界荷载系数，从而得出穿层柱的计算长度系数。

该方法的缺点是不能考虑各约束之间的耦连作用以及结构其他部位对穿层柱的间接约束作用，而得到构件的计算长度系数值都相对偏大，所以一般不采用该方法确定穿层柱的计算长度系数。

4 工程概况

本工程抗震设防烈度为8 度，场地类别为Ⅲ类，设计地震分组为第一组，基本风压为0.40kN/m，地面粗糙度类别为B 类，结构阻尼比取0.05，水平地震作用系数最大值α=0.16，特征周期T=0.45s，抗震等级为一级，楼板按弹性板考虑。

典型的结构平面布置图如图1 所示，红色部分为穿层柱，一层层高为5.8m，二层层高为5.4m，三到五层层高为4.5m，五层以上层高为3.8m，总层数为13 层，结构总高度为55.1m。穿层柱共穿越底部3 层，构件的几何长度为L=5.8+5.4+4.5=15.7m，穿层柱的直径为1000mm，材料为C55。

图1 结构平面布置图

5 结构分析与计算

5.1 整体结构的屈曲分析

分别采用PKPM、YJK、Midas 软件，建立整体模型，对整体结构进行线弹性屈曲分析，屈曲荷载取用荷载标准值（1.0恒+1.0 活），相关模态如图2。屈曲分析结果如表1。

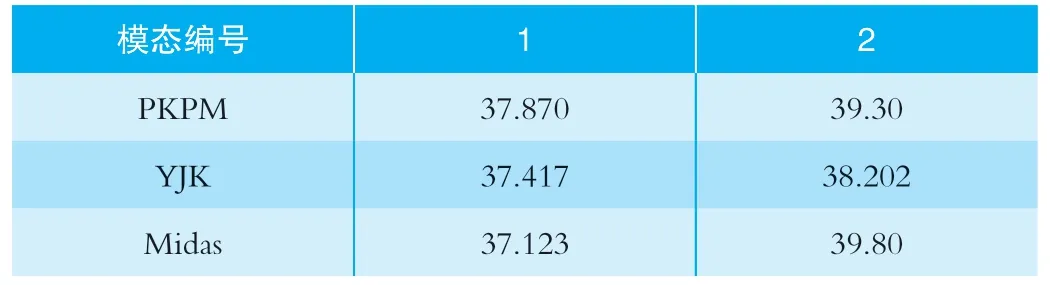
表1 PKPM、YJK、Midas 整体屈曲因子对比

5.2 整体结构的屈曲分析—单位力法

分别采用PKPM、YJK、Midas 软件，建立整体模型，进行整体结构的屈曲分析，屈曲荷载取用在穿层柱柱顶施加单位集中力（P=1kN），相关模态如图2 所示。屈曲分析结果如表2 所示。

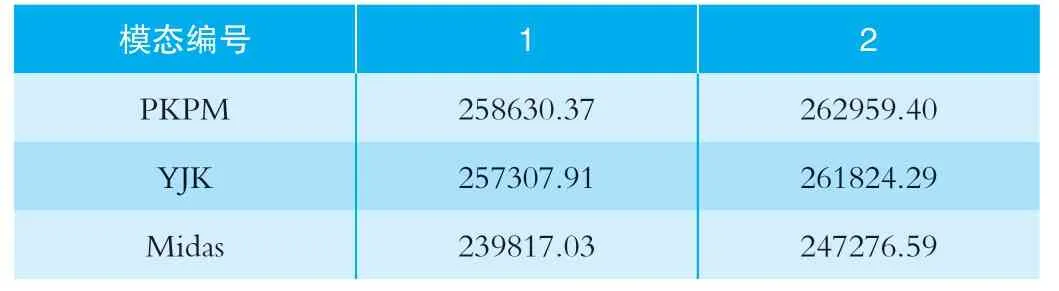
表2 PKPM、YJK、Midas 整体屈曲因子对比

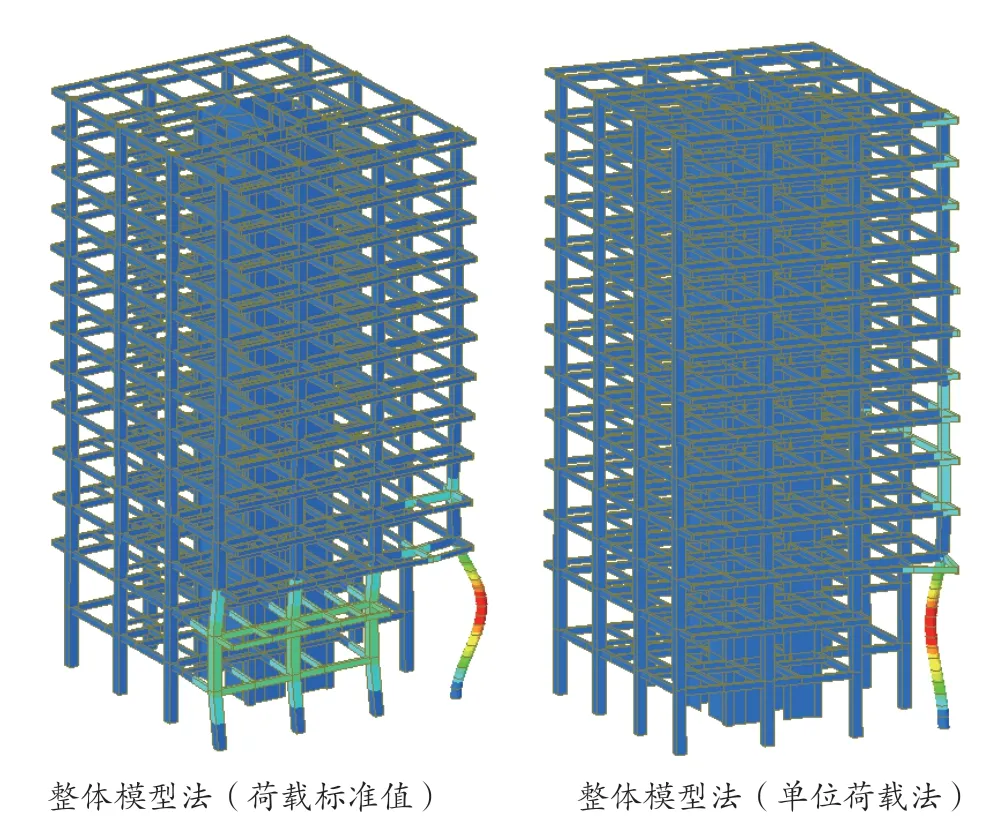
图2 整体模型分析

5.3 结果对比

通过结果对比发现，两种方法得到的计算长度系数几乎相同，详见表3。

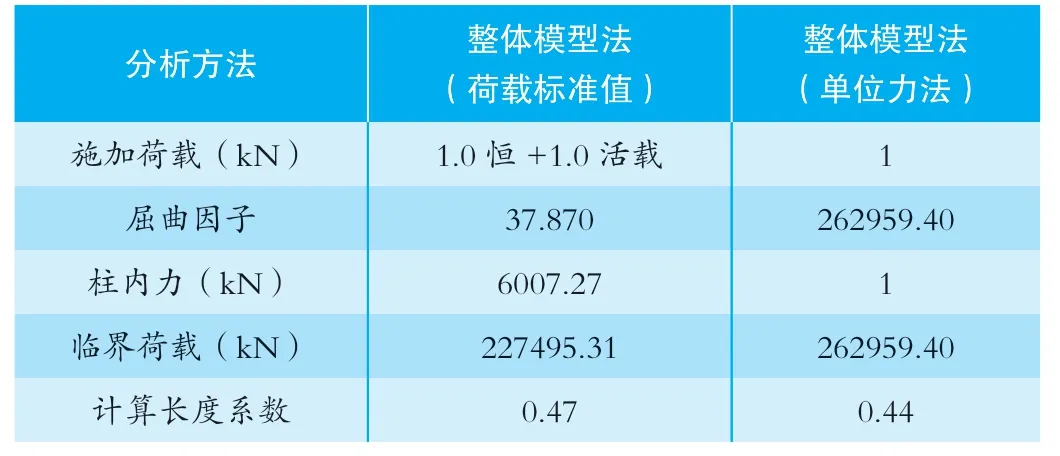
表3 PKPM、YJK、Midas 整体屈曲因子对比

6.结束语

通过对穿层柱的线弹性屈曲分析，计算结果发现关于穿层柱的计算长度系数远小于规范的规定值（1.0），所以对于穿层柱来说，穿层柱的计算长度系数一般均采用规范值来进行设计，其设计结果是安全可靠的。