让数学活动课“生动”起来
胡伟

《整式加减数学活动》是人教版数学七年级上册第二章整式加减新课结束后的数学活动课。本节课旨在类比“数”来学习“式”的运算,让学生会用整式和整式加减运算表示实际问题中的数量关系。
一、巧用数形结合,找准变量关系
解题时,找准变量关系一直是学生学习的难点。教师巧用数形结合,能让学生通过直观的图形从不同角度去分析,进而发现题目的变量关系。
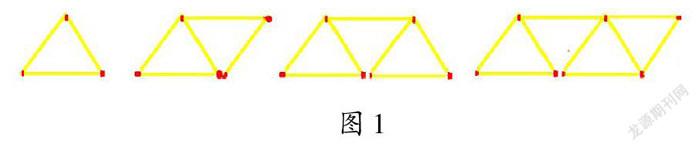
例如,教学活动1时,笔者出示用火柴拼成的一排由三角形组成的图形(如图1),并提问:“下图是用火柴组成的三角形,分别为1、2、3、4个,请问每增加一个三角形,需要增加几根火柴?如果有n个三角形,需要多少根火柴?”
学生甲回答:第1个三角形要用3根火柴,每增加一个三角形需要增加2根火柴,3个三角形一共需要“3+2+2”根火柴。笔者继续提问:还有没有其他计算方法?学生乙回答:把第1个三角形的第1根看成定量,其他三角形都是增加2根火柴得到的,所以3个三角形一共“1+2+2+2”根火柴。笔者追问:两个变量(三角形个数和增加的火柴的根数)有什么数量关系呢?学生丙回答:增加的火柴的根数是三角形个数的2倍。笔者及时肯定了学生的回答,又继续引导:那么5个、10个、20个、n个三角形一共需要多少根火柴呢?学生总结:增加的火柴再加上1就行了,即1+5×2、1+10×2、1+20×2、1+n×2。
在此基础上,笔者引导学生把三角形个数和所需火柴的根数对应起来并制成表格,让学生观察哪个是不变的量。学生通过观察,发现每增加一个三角形,要增加2根火柴,所以第一个三角形的第一根火柴可作为不变的量,即规律为:2×1+1,2×2+1,2×3+1,2×4+1,…,2n+1。
二、运用分类讨论,归纳验证规律
分类讨论的方法,有利于探索、验证问题中的规律。我们来看活动2的教学过程。笔者出示某公园的门票价格,如下表。
光明中学七年级两个班的学生去公园游玩,一班有48人,二班有55人。(1)每个班都单独购票,各需要多少元?(2)两个班一起购票,怎样购买门票更省钱?能省多少钱?(3)如果一班有x人,怎样求购买门票的钱呢?
教学中,笔者充分引导学生分类讨论:若你是一班班长,怎样购买门票更省钱?学生甲回答:用48乘对应的票价25。学生乙回答:还能按22元的票价,也就是多买3张票,凑够51。笔者追问:如果两个班都买,怎样购买最省钱呢?学生丙回答:因为两个班人数合在一起超过100人了,所以按20元一张的票价买。笔者因势利导:如果一班有x人,怎样求购买门票的钱?学生丁回答:分3种情况,x的大小不一样,列式也不一样,如果x≤50,则门票钱为25x;如果51≤x≤100,则门票钱为22x;如果x﹥100,则门票钱为20x。
为了更好地巩固学生的分类讨论的思想方法,笔者出示第2道例题:一种笔记本售价是2.3元/本,如果一次买100本以上(不含100本),售价是2.2元/本,请列式表示买n本笔记本所需钱数(注意对n的大小有所考虑)。笔者引导学生讨论下面的问题:①按照这种售价规定,会不会出现多买比少买反而付钱少的情况?②如果需要100本笔记本,怎样购买能省钱?学生通过分组对问题进行分类讨论、探究,提出疑问:笔记本的单价是不是固定不变的2.3元?笔记本的单价由什么来确定?通过讨论学生得出:笔记本的单价由所购买笔记本的数量来确定,买不同的本数就有不同的单价。买50本所需的钱为50[×]2.3=115(元);买100本所需的钱为100[×]2.3=230(元);买101本所需的钱为101[×]2.2=222.2(元);買200本所需的钱为200[×]2.2=440(元)。笔者总结:当n≤100时,钱数为2.3n;当n>100时,钱数为2.2n。
三、体验探索归纳,达成深层理解
在教学活动3——月历的数学时,笔者采取观察和体验相结合的办法,引导学生由浅入深、由特殊到一般地探索、归纳规律,并利用规律解决实际问题,达成深层理解。
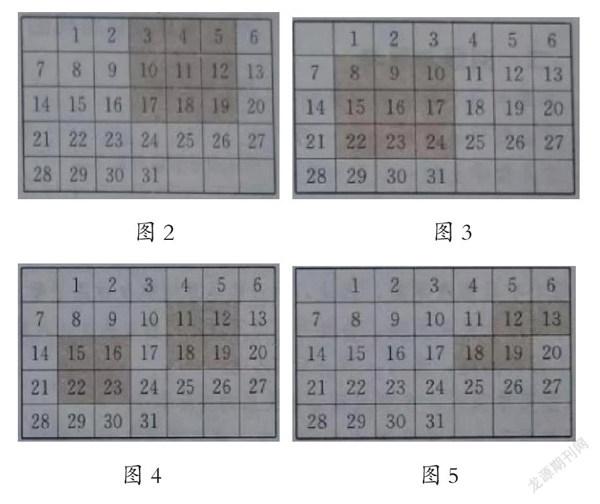
笔者先出示如下四份月历图:
随后出示如下6个问题:①图2中带阴影的方框中的9个数的和与方框正中心的数有什么关系?②如果将图2带阴影的方框移至图3的位置,问题①中的关系还成立吗?③不改变带阴影的方框的大小,将方框在月历中任意移动几个位置,结论依然成立吗?④这个结论对于任何一个月的月历都成立吗?⑤如图4,两个带阴影的方框里的数分别是4个,你能得出什么结论?⑥如图5,对于带阴影的框中的4个数,你又能得出什么结论?
出示问题后,学生通过观察、计算迅速得出:图2、图3带阴影的方框中的9个数的和是方框正中心的数的9倍。笔者追问:月历上的数的大小与排列有什么特点?为什么会出现9倍这样的结论?怎样根据实际情况设未知数x,列代数式证明这个结论?一名学生回答:若设正中心的数字为x,其他8个数加在一起的和为(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x,9个数相加的和为9x,是最中心的数的9倍。
笔者肯定了学生的回答,让学生继续通过分组探索,归纳出其他几个问题的答案。问题①中,图2阴影框里的9个数之和为3+4+5+10+11+12+17+18+19=11+22+22+22+22=99,即方框内9个数字的和为99,恰好是正中心数字11的9倍。因此,11恰好是方框内9个数字的平均数。问题②中,图3中方框内9个数之和为8+9+10+15+16+17+22+23+24=16+32+32+32+32=144,即方框内9个数字的和为144,恰好是正中心数字16的9倍。因此,16恰好是方框内9个数字的平均数。因此,问题①的结论依然成立。问题③中,随意将方框移动几个位置,方框内9个数字的和依然是正中心数字的9倍,正中心数字依然是方框内9个数字的平均数,结论依然成立。问题④中,这个规律对任何一个月的月历都成立。对于问题⑤和问题⑥,学生得出的结论是:图4和图5阴影框中的4个数,“对角线”上的两个数的和相等。
学生总结后,笔者引导学生在挂历上任意找一个月,框选9个数或4个数,实际体验并且计算验证。学生验证后,笔者再进行深层次的引导:如果月历中每行按照奇数个数排,7个日期一行,或者是按照偶数个数排,6个日期一行,再框选其中的9个数或4个数,还有这样的规律吗?学生通过探究得出同样的规律。
(作者单位:枣阳市鹿头镇吉河中学)
责任编辑 张敏

