羊群体运动元胞自动机模型中的最小势能分析
焦帆,聂丽丽,王瑛,刘振宇*
(1.山西农业大学 信息科学与工程学院,山西 晋中 030801;2.山西农业大学 农业工程学院,山西 晋中 030801)
动物群落的群体现象受到广泛关注,有学者对鱼群、兽群、微生物等个体的群体运动进行了深入研究。研究结果表明一些规律对动物的群体现象有着重要影响[1-3],例如安培定则的“靠近排斥,远离吸引”自然规则对于御敌、聚集、繁衍、适应环境有重要作用[4]。动物的群体运动不仅是单纯的无数个体组成,而且由个体间互相协同传递信息组成的。Couzin I D等[5]研究了个体间相互作用动力导致的动物集体行为并提出了相关模型表明个体与群体联系[6]。唐敏等[7]通过对群体运动的建模分析表明群体运动对个体的发育和健康至关重要。Gueron等[8]的研究表明个体行为会受到相邻个体行为影响,并且彼此的信息会逐层传递。目前群体行为分析方法使用较多的是对某些特征进行识别和提取。J.buhl等[9]对沙漠幼虫的观察就是特征提取通过统计力学来研究群体动物。
以前的研究大多提出复杂的模型,且对群体多种运动状态分析不足,在分析二维三维影响以后,本文构建了基于元胞自动机和最小势能的优化二维模型,通过数值模拟研究势能在羊类群体运动中发挥的作用以及个体之间相互的协同在限定空间内形成的运动状态的影响[10]。
1 材料和方法
1.1 试验材料
1.1.1 元胞自动机
元胞自动机(cellular automaton,CA)是一种时间、空间、状态都离散,空间相互作用和时间因果关系为局部的网格动力学模型,具有模拟复杂系统时空演化过程的能力[11]。它已经被应用于道路、铁路、人员疏散、物流等各个领域[12-15]。不同于一般的动力学模型,元胞自动机不是由严格定义的物理方程或函数确定,而是用一系列模型构造的规则构成。凡是满足这些规则的模型都可以算作是元胞自动机模型。因此,元胞自动机是一类模型的总称,或者说是一个方法框架。其特点是时间、空间、状态都离散,每个变量只取有限多个状态,且其状态改变的规则在时间和空间上都是局部的[16-17]。
元胞自动机系统是一个由元胞空间、元胞状态、邻居和变化函数规则等组成的离散动力学系统(图1)。元胞是空间划分以后所得的最小单位,在任一时刻每个单元只有一种元胞状态;邻居会影响中心元胞下一个时刻的状态;变化函数定义了元胞状态转化的规则[18]。模型可定义为:
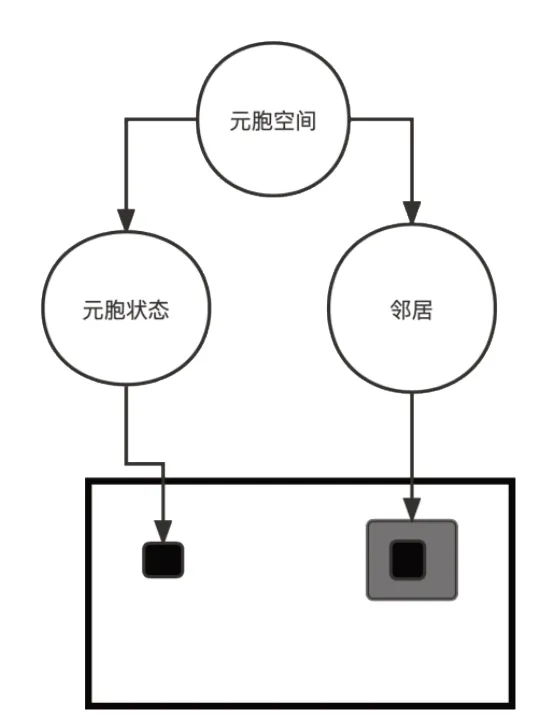
图1 元胞机组成Fig.1 Composition of metacell machine
式中CA代表元胞机;Ω是离散的元胞空间;S是元胞状态;N是元胞领域;F是变化规则,即按照前一时刻元胞相邻状态组合确定当前状态的函数。
1.1.2 实体对照羊群
依据羊圈设计导则和基本要点制作对有限空间内的杜泊羊群进行研究,根据实际需求设立模型尺寸,试验模型实体以300 m×300 m的羊圈平地中的100头羊为研究体,由于圈养时间已经2年所以不考虑环境适应性问题,试验中利用摄像机对其进行摄像记录。
1.2 试验方法
1.2.1 基于势能的元胞自动机建模理论
势能可以理解为储蓄在一个单位自身内部的能量,同时也能输出和转变为不同的形态力量。势能是一种状态量。势能属于可以相互作用的物体,并不是单单个体所占有。势能按作用性质的不同,可分为引力势能、弹性势能、电势能和核势能等,此处羊群的势能主要讨论距离势能和角度势能。
由于视觉是羊群中直接感受到周围环境和对象获取信息的直接方式,而周围环境以及邻居数量和邻居行为都会影响个体行为的决策[19]。所以首先假设羊只个体视觉是常值(不变,有限),羊只的参考邻居会在距离最近的N个个体中选择。
本研究中羊群的个体势能由距离势能和角度势能组成。则羊的个体势能为Ei,角度势能为Eih,距离势能为Ei_dj,假定一共有30头羊,运动方向示意图如图2所示。
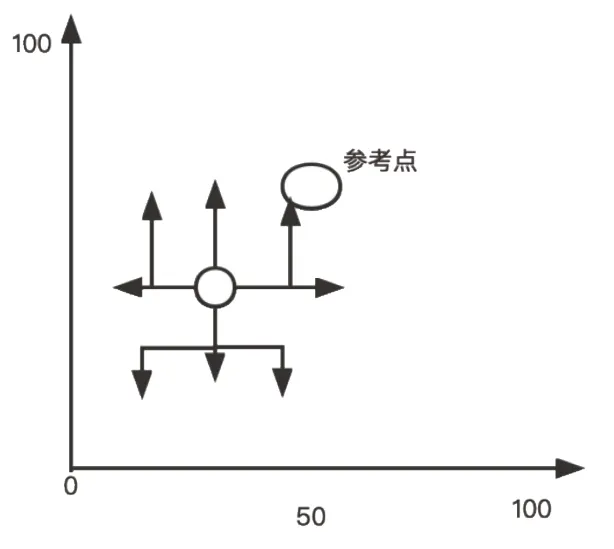
图2 运动方向示意图Fig.2 Schematic diagram of the direction of motion
则个体势能表达如下[10]:
式中n为参考邻居数量,Ei_dj,Ei_θj分别表示个体i到参考邻居j的距离和角度产生的势能。
个体角度势能表达如下[10]:
式中Ei_dj为个体i自身势能,其中k是系数,θih表示i下一时间运动方向与水平面夹角。
个体到参考距离势能表达如下[10]:
式中Ei_dj是个体到参考距离势能,H是阶越函数,kd1,kd2为系数,R0为常数表示个体i到j之间的最佳距离,dij为个体i到j的距离。
个体到参考角度势能表达如下[10]:
式中Ei_θj为个体到参考角度势能,kθ1,kθ2为系数。
1.2.2 元胞机更新规则
本文选取时间离散为各个时间步,把虚拟羊所在元胞空间设定为100×100,区域划分为n×i个相同的正方形区域,一个区域只有一个元胞,这些正方形区域合起来就是羊群的二维元胞空间,羊只个体随时间发展可能运动的位置再次划分为9个位置。本文定义的移动规则如下几个步骤:
1)假定当前时间为t,虚拟羊只个体确定元胞空间范围内内所有参考羊只和下一步全部可能的位移地点。运动方向如图2所示;
2)核算接下来t+1时间的9个移动方向势能,关系式如(1)~(4)所示;
3)分析上一步所有位置势能大小,得到最小势能移动方位,并确定为下个t+1时间移动初始位置;4)通过步骤1~3遍历所有虚拟羊只;5)覆盖旧位置,更新画布,并重复1~5。
1.2.3 羊类感应范围
羊类的感应范围则在320~340之间,试验模拟羊类视野范围感应周围同类的能力。对于每个Agent的感应范围如图3所示:以元胞空间当中的羊只个体Agent为中心,感知范围是半径为r的元胞空间,则其到参考点的最小距离表示为:
图3 羊群感应范围Fig.3 Flock sensing range
式中p是当前位置,m是周围的9个元胞空间,i是0~9的变量。
1.2.4 行为规则
如图4所示,羊只运动时会运动到元胞空间周围的9个点,即表示为[−1,−1][−1,0][1,1][0,−1][0,0][0,1][1,−1][1,0][1,1]。9个方向的运动趋势取决于到附近参考点的距离,此处代表距离势能。羊群总计归纳为以下几类行为:

图4 运动方向示意图Fig.4 Schematic diagram of the direction of motion
1)随机行为:由于未考虑羊类外界的全部影响因素,所以羊类运动初始可能是随机的,整个活动全过程头羊有可能在任意方向走动;
2)避障行为:羊群运动过程中可以通过宽广的视线感知障碍的出现,在模型中表示为当有障碍出现在Agent感应区域,则它不会向着障碍物运动;
3)随波逐流:羊类通过最小势能点跟随最近的羊只进行运动避免大量消耗自身能量,俗称羊群效应;
4)加速行为:当羊群的头羊感知到危险等情况会进行冲刺,此时所有羊都会随着一起进行冲刺行为,表现为运动加速。
2 结果与分析
2.1 实体结果
由上述监控设备可以看出环境变化对羊群可以形成一种刺激,当对头羊进行干预时羊群会出现转圈现象,监控部分截图如图5所示,a和b为夜晚群体运动过程,c和d为白天群体运动过程,在羊群无序到有序的过程中,羊群从休息时散乱随机的混乱状态下,某个体首先进行某项行为,随着时间的流逝加入群体运动的独立个体持续增长,最终从散乱的随机行为转变为统一聚集的的进食或者移动行为。群体旋转状态形成时,羊群中个体近乎平均分布。

图5 羊群活动图Fig.5 Herd Activity Chart
2.2 模拟与结果
研究对真实的羊群观察发现当羊群受到刺激或者环境改变时会出现群体聚集比如旋转的行为,为了研究羊的群体运动驱动原理,假定羊群的运动模式由势能控制,试验结合能量原理创建了基于最小势能的羊群运动函数式,依据函数式使用Python建立一个二维元胞自动机模型[20]。通过公式(1)~(4)利用数值模拟与羊群运动状态对比验证本模型合理性。
为了体现羊群运动的真实性,选取在自然条件的300 m×300 m正方形场地内,其具有一定数量随机的树木存在,宽度为0.5~1 m,其余均与自然条件下无差进行对照试验。设参考邻居j通过角度影响个体i的位置、方向和相互的距离,当系数处于某些范围时模拟的羊群就会变成聚集的饮食或者其它活动。选取时间离散为各个时间步,试验中模拟的数值对象为所在元胞空间100a×100a的30只羊,系数设 置 为kθ1=1.5×107,kθ2=8×107,kd1=3.0×104,kd2=2.0×107,kh=7×1010,R0=1a。所 有羊只初始位置以及运动形态皆不做规定即随机可变,区域划分为n×i个相同的正方形区域,一个区域只有一个元胞,这些正方形区域合起来就是羊群的二维元胞空间。随机分布初始如图6所示。同时有3种属性分别附着在每个元胞上,即羊个体,障碍以及危险(其它生物恐吓)。以Mls,xls,yls分别表示(x,y)位置的单个元胞的运动速度,x以及y轴方向的运动速度。则羊群状态合集表现为:
图6 随机分布初始图Fig.6 Initial plot of random distribution
Agent被作为元胞空间中状态为羊的个体,同时网格如图3在几何上也表示羊个体的质心。
Agent移动规则会在下一时间移动到其临域范围内的引力最大位置,但试验过程中会发现羊群的运动会和预期不符的沿着相似轨迹上溯,所以此处考虑羊类行为随机性的思想,加入到羊群运动中。在模型中会模拟羊进行相应的行为运动。同时建立了羊群与环境的关系,计算Agent(元胞中羊只个体)下一时间运动到下一区域的概率,使用随机函数和概率以及势能结合最终确定Agent(羊只)下一时间步所在的位置。
Agent向M方向运动的概率为(7)所示:
式中i表示元胞空间属性,如遇到障碍时表示为i=0,否则i=1;Prw(M)表示为在r场景下的元胞吸引力概率,r=1则羊只处于感应场景,r=2羊只处于匀速缓慢前行,r=3羊只处于快速移动情景。
式中Ar是r场景下8个方向的吸引力权重和;images/P43_6791371.jpg(M)是r场景下l行为在M方向的吸引力权重,lϵ(1,3),分别代表1.2.4章节中的随机,避让,随波逐流。
如图7所示,在过程中会先分为多个小群体最后慢慢聚集成一整个大的群体运动。也存在个别个体脱离群体运动,独立运动,同时也有个别个体脱离群体以后又重新加入群体运动,对比虚拟羊群与真实羊群的群体运动以及形成过程,发现本模型的虚拟羊群与真实羊群现象相符。
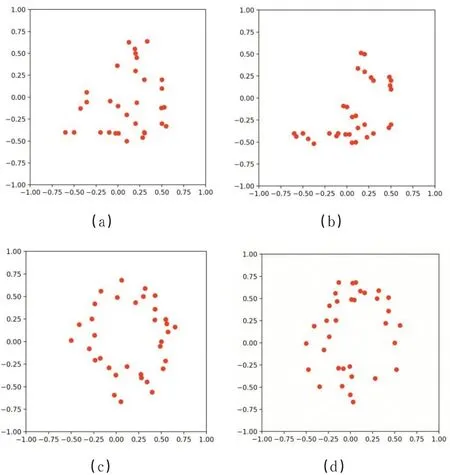
图7 元胞机模拟羊群中旋转群体状态Fig.7 Rotating group states in a metacomputer simulation flock
3 讨论
群体运动在自然界作为最普遍的自然现象,由许多自治个体的组合而成,在没有集中管理控制下大多通过个体有限范围的感知和相互作用形成群体运动现象,包括宏观的天体聚集形成的星系运动,生物中的鱼群、大雁南飞、蚂蚁聚集等。微观的微生物和细菌等群体运动。即使生物界中每个个体的感知范围和智商都有限,但集中起来却能展现出多种复杂的群体运动。
仿真模拟尽管可以在大体上得出与观察相似的现象结论,但是将实际情况与仿真情况具体定量比较还是具有一定挑战性[21]。所以此处势能始终具有很多的系数条件范围才能达到模拟结果。模拟形成了一个基于最小能量原理创建的元胞机来模拟羊群体运动,为探索动物间的群体运动提供了相应的架构。具体参数的值以及势能范围还需要进一步的探究。群体运动的系统研究具有重大意义,首先它是研究生物复杂性的一个方法,其次可以通过自然界的智慧将分布式用到智能设备发展中如多机器人协调控制等。通过对这些个体系统的控制规律设计可以使整体系统达到期望的群体行为,同时对工程也有潜在研究价值。
4 结论
依据羊群在真实环境下的运动状态,假设羊群在更大范围内的运动总是依靠所有动物都有的最小势能驱动,以旋转运动为特征,通过对羊只外界环境变化刺激进一步分析,对应得出了最小势能函数并将其与元胞机融合模拟。由于试验与数值高度弥合,所以能够证明本模型能够有效的反应有限空间内羊群体行为形成机理。将群体运动分开解析,通过最小能量与元胞机的融合构建模型,通过对系数值的改变模拟出不同的群体聚合运动轨迹,推断能量守恒定律和最小能量原理在羊群中是其要遵守的根本规则。得出以下结论:
(1)个体的运动趋势会受到周围个体的影响,其中影响因素包括角度、距离、个体能量;
(2)当群体基数大的时候,个体受到的周围影响会增大,参考邻居p的数量在5~9之间时会出现旋转转圈现象,数值模拟与实验视频观察现象具有较高一致性,表明本模型能够有效反映限定空间中羊群旋转运动的形成机理;
(3)羊群居行为极强,通过周围熟悉的羊只建立小群体,构成大群体最终保持群体运动行为;
(4)Agent模型能够通过随机、避碍、随波逐流、冲刺等集中行为来体现羊的运动特性。
本研究为动物间群体运动驱动机理提供了一个参考模型,为进一步探索群体效应与能量原理之间的关系奠定了理论基础。同时为群体智能、群体控制工程方面提供了新思路。
——《势能》

