融合统计学习与深度学习的猪舍环境预测模型
马超凡,谢秋菊*,王圣超,李佳龙,郑萍,包军,刘洪贵
(1.东北农业大学 电气与信息学院,黑龙江 哈尔滨 150030;2.东北农业大学 动物科技学院,黑龙江 哈尔滨 150030;3.农业农村部生猪养殖设施工程重点实验室,黑龙江 哈尔滨 150030;4.黑龙江省猪种质与生产技术集成创新工程技术研究中心,黑龙江 哈尔滨 150030;5.教育部北方寒区智能化繁育与养殖工程研究中心,黑龙江 哈尔滨 150030)
在规模化畜牧业中,舍内环境是影响牲畜生长繁衍和生产性能的重要因素。氨气(NH3)是一种无色具有刺激性气味的碱性气体广泛存在于畜禽舍中,猪、鸡、羊等对NH3刺激比较敏感的动物,会受到NH3的影响而发生呼吸系统疾病[1]、消化系统疾病和营养代谢疾病[2]。二氧化碳(CO2)主要来自于牲畜的呼吸[3],浓度过高时会使牲畜食欲下降和生长发育减缓。温度是猪舍环境的另一个重要指标,温度过高或者过低都会使猪维持体温能量消耗增大,降低猪的生产性能[4]。及时、精准地预测猪舍氨气浓度、二氧化碳浓度和温度,对于改善猪的生存环境具有十分重要的实际意义。
畜禽舍环境因子预测模型可分为基于理化统计和机器学习算法2大类。基于理化统计模型从物理化学的角度进行分析,这类模型往往需要进行大量的试验,且对试验数据的精确性要求比较高,但是得到的预测模型迁移性较差并且往往不稳定,难以得到精准的预测结果[5-6]。基于机器学习方法的禽舍内环境因子预测模型,常见的有回归模型[7-8]、灰色系统理论[9]、ANFIS模型[10-11]、神经网络模型[12]。其中,循环神经网络(RNN)[13-14]对时间序列具有较强的学习能力,可以很好的提取到时间序列中的非线性关系演变。
然而,RNN对序列中的长时间依赖性捕捉能力比较差,为解决这一问题,长短时记忆网络(LSTM)[15]在RNN的基础上,将隐藏层的神经元换成了细胞状态和3个门结构,实现了控制信息的记忆和遗忘,实现对畜禽舍内环境因子的动态预测[16]。在这些模型中,以减少模型输入变量、降低模型复杂度,提高模型的预测精度为主要目标,有学者提出了融合随机森林与长短神经网络(RFLSTM)的猪舍氨气浓度预测优化模型[17],融合注意力机制的LSTM模型[18],较好地获取畜禽舍环境变量之间的依赖性和环境变量数据序列的时间依赖性。此外,经验模态分解与LSTM结合起来的EMD-LSTM模型[6],可使氨气序列从非平稳序列转换为平稳序列,充分发挥了LSTM神经网络数据处理的优势;将一维卷积神经网络(CNN)与LSTM融合的CNN-LSTM模型较好地实现了时序充序列特征提取[19-21]。为了避免陷入局部最优,麻雀搜索算法(SSA)、粒子群优化算法(PSO)、遗传算法(GA)等优化算法被用来对神经网络的超参数进行寻优以提高神经网络预测精度[12,22]。
门控制循环单元(GRU)[23]模型是LSTM模型的优秀变体,结构更简单,可在一定程度上减少迭代时间,提高模型预测效率。但在畜禽舍环境因子时间序列中,除了一些内在的非线性的特征外,还需要提取时间序列数据的线性关系,ARI⁃MA模型具有很好线性关系捕捉及处理能力[24-25]。
为更全面地提取及处理复杂的畜禽舍环境因子时间序列特征,本文融合ARIMA和GRU模型的线性及非线性特征提取的优势,提出一种线性与非线性方式融合的ARIMA-GRU猪舍环境因子预测模型,提升NH3浓度、CO2浓度和温度预测模型的性能,为猪舍环境控制提供可行的参考。
1 材料与方法
1.1 试验材料
本文数据来源于黑龙江省哈尔滨市江北区某养猪场妊娠猪舍,从2022年1月26日到2月20日共26 d天的环境参数(温度、NH3和CO2浓度)。该猪舍大小为24.8 m×16.2 m×2.4 m(长×宽×高),舍内共有160个限位栏,饲养130头妊娠母猪,限位栏大小为2.2 m×10.66 m×1.06 m(长×宽×高)。猪舍平面结构如图1如示。

图1 猪舍平面结构Fig.1 Plane structure of the piggery
猪舍环境控制系统以STM32F103VET6芯片为核心,传感器数据采集间隔为1 min。首先将缺失的数据采用线性插值法进行插值,然后将异常点替换为其前后2侧采样点的均值。异常点指的是其值与其平均值之差的绝对值大于其标准差的3倍的点。环境参数数据如图2所示,NH3浓度最大为37.8 mg·L-1,最小为8 mg·L-1,平均为20.28 mg·L-1;二氧化碳浓度最大为4961 mg·L-1,最小为1608 mg·L-1,平 均 为3281 mg·L-1;温 度 最 大 为17 ℃,最小为13.2 ℃,平均为15.3 ℃。
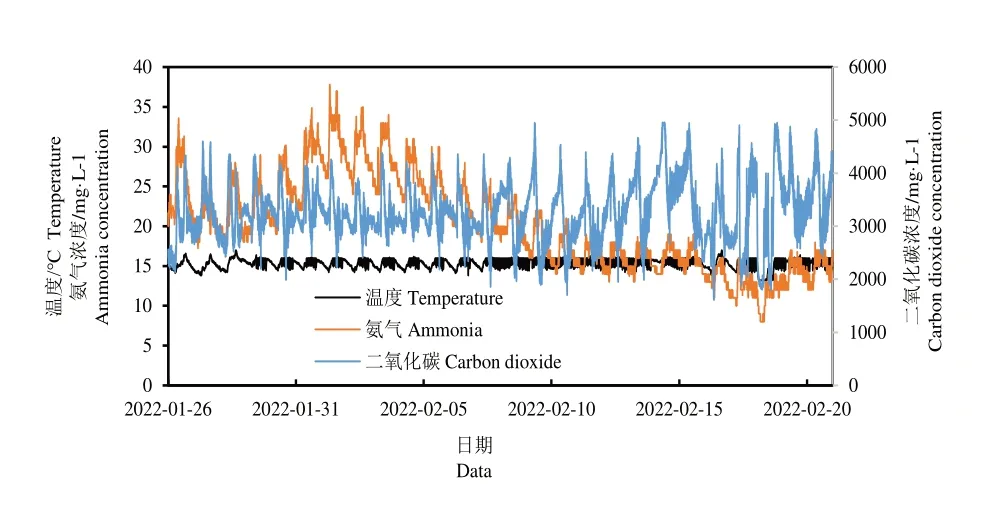
图2 环境参数变化曲线图Fig.2 Variation curve of environmental parameters
1.2 试验方法
环境因子时间序列是由线性序列和非线性序列组成的,传统的时间序列预测往往采用单一的模型,比如GRU模型、CNN模型、ARIMA模型,但是单一的模型面对猪舍环境因子序列这样复杂的序列往往预测效果较差,本文采用的ARIMAGRU混合模型预测分为2个阶段,第1个阶段是统计模型ARIMA对环境因子时间序列中的线性关系进行拟合和分析,第2阶段是GRU对ARIMA预测后产生的残差进行预测,组合模型结合了2个模型的优点,拥有更好的预测效果(以NH3浓度时间序列为例,CO2浓度时间序列和温度时间序列预测方法按照相同的步骤)。
1.2.1 ARIMA模型
ARIMA模型是由自回归滑动平均(ARMA)模型与差分模型组合而成的,而ARMA模型又由自回归(AR)模型和移动平均(MA)模型组成[24-25]。ARIMA(p,d,q)模型主要用于非平稳时间序列的预测,对非平稳的氨气时间序列进行d阶差分运算得到平稳的氨气时间序列,再将得到的平稳氨气时间序列输入ARMA(p,q)模型进行预测。ARIMA模型的数学表达式见公式1:
式中∇d=(1-B)d为高阶差分;Θ(B)=1-θ1B-θ2B2-…-θqBq为ARIMA模型的移动平均多项式,Φ(B)=1-φ1B-φ2B2-…-φpBp为ARIMA模型的自回归系数多项式。
使用ARIMA模型对氨气时间序列进行预测的步骤如下:
步骤1:平稳性检验。如果时间序列是非平稳的,使用差分法对序列进行处理。一阶差分后,对序列的平稳性进行检验,如果序列为平稳序列进行下一步处理,否则继续进行差分运算直到平稳。Augmented Dickey-Fuller(ADF)单位根检验是时间序列平稳性检验的常用方法,对序列特征不明显的数据也具有很好的识别效果,ADF单位根检验统计量的P<0.05,检验通过,序列为平稳序列,否则为非稳定序列。
步骤2:ARIMA模型参数确定与检验。在ARIMA(p,d,q)模型主要参数中,d为步骤1中进行的差分次数,p为自回归项数,q为滑动平均项数。d确定后通过AIC函数(赤池信息准则)进一步选择p和q,通常认为AIC值越小的ARIMA模型效果越好,同时需要对差分后的序列进行白噪声检验,白噪声检验一般采取Ljung_Box方法,检验统计量的P<0.05,序列为非白噪声序列,否则回到步骤1进行差分,最后对模型进行建立和预测。AIC函数表达式见公式(2),ARIMA模型建立流程图见图3:

图3 ARIMA建模流程图Fig.3 Flowchart of ARIMA modeling
式中k指的是参数的个数,L指的是似然函数。
1.2.2 GRU模型结构
ARIMA-GRU模型中GRU模型由输入层、隐含层和输出层组成,隐含层由3个GRU层和1个全连接层组成。将ARIMA预测氨气序列之后计算得到的残差经过标准化之后传入输入层,输入层接收数据之后传入GRU层,GRU层学习氨气残差序列之间的依赖关系,经过3层GRU层之后输出的信息维度为64,然后传入全连接层,经过非线性变化,提取序列之间的关联,最后通过输出层输出预测值。GRU神经网络结构见图4。

图4 GRU神经网络结构Fig.4 Neural network structure of GRU
GRU神经单元总体结构与LSTM神经单元比较相似,信息的保存、更新和舍弃通过门结构来进行控制。LSTM具有3个门,分别是遗忘门、输入门和输出门,但是GRU只有更新门和重置门,没有设置细胞记忆状态,因此与LSTM相比,GRU具有更简单的网络结构,更少的计算量和更高的训练效率[26]。GRU网络单元如图5所示:
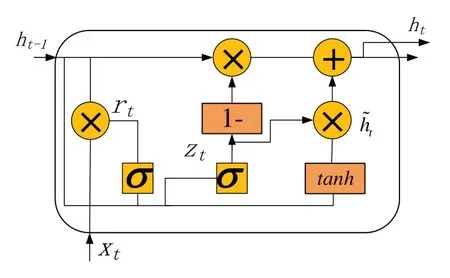
图5 GRU神经单元结构Fig.5 the Gru cell structure
GRU神经单元由更新门zt和重置门rt2个门组成,重置门控制了上一节点信息的保存程度,更新门控制着前一节点与当前节点信息的保存比例。首先需要计算重置门和更新门的值,将上一个节点传递下来的隐状态ht-1和当前节点的输入值xt输入sigmod函数进行计算,得到更新门和重置门的值,进而对门进行控制,更新门和重置门的取值范围都在0到1之间。然后计算当前节点状态,将重置门和前一节点的输出ht-1对应元素相乘,再与xt相乘,通过tanh函数变换得到当前节点的状态h͂t,最后对当前节点的输出ht进行计算[27]。计算过程见以下公式(3)~(6):
式中,xt为输入值,zt为更新门,rt为重置门,ht-1为上一个节点传递下来的隐状态,h͂t为当前节点状态,br、bz和bh为偏置,σ为sigmod函数。
1.2.3 CNN模型
为了验证ARIMA-GRU模型的性能,本文选取CNN模型作为对照之一,CNN模型由输入层、隐含层和输出层组成,模型结构见图6。经过处理后的时间序列传入输入层,输入层接收数据之后传入一维卷积层,一维卷积层可以提取序列之中的子序列,但是不能捕获时间依赖性;经过2轮的卷积、池化,信息最后传入全连接层,经过非线性变化,输出预测值。
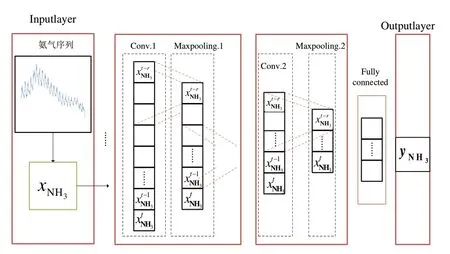
图6 CNN神经网络结构Fig.6 Neural network structure of CNN neural network
1.2.4 ARIMA⁃GRU模型
首先将经过处理后的猪舍氨气浓度数据序列X={x1,x2,x3,…,xn}输入ARIMA模型,ARIMA模型对序列中的线性部分进行分析和拟合得到预测结果Y={yn+1,yn+2,yn+3,…yn+k},然后通过计算得到猪舍氨气浓度预测残差e={en+1,en+2,en+3,…,en+k},将 残 差 输 入GRU神 经网络对残差进行训练和拟合,得到残差预测结果images/P33_6761371.jpg最 后 将2个 模 型 预测结果进行相加得到最终预测值,流程见图7。

图7 ARIMA-GRU建模流程图Fig.7 Flowchart of ARIMA-GRU modeling
1.3 统计分析
本文采用均方根误差(RMSE)、决定系数(R2)和平均绝对百分比误差(MAPE)对模型的性能进行评估,公式见(7)~(9):
式中y为实际值,ŷ为预测值,m为样本个数,yˉ为均值。
2 结果与分析
2.1 数据处理以及试验环境
选取前90%的数据作为训练集(其中训练集中划分20%作为验证集),后10%作为测试集,环境数据采集间隔为1 min,由于短时间内环境因子变化不明显,用每30个采样点的平均值替代原本的30个采样点,使数据的时间间隔变为30 min,将当前时刻的环境因子输入模型,模型对30 min后的环境因子进行预测。将数据导入模型前,需要对数据进行归一化处理,这样有利于模型的训练,预测得到的数据可以使用反归一化来恢复。
试验环境在Python3.6和Tensorflow-GPU 2.5.0下完成。硬件环境中CPU采用AMD Ry⁃zen 7 5800H,主频为3.2 GHz;GPU采用NVIDIA GTX3070,7 G显存。
2.2 模型参数设置
由图2可见氨气时间序列为非平稳时间序列,为进一步确认,对氨气时间序列进行ADF单位根检验,由单位根检验结果可知,p取值为0.419,大于0.05,所以为非平稳序列。对该序列进行1阶差分后进行ADF单位根检验,p取值为4.19×10-20,小于0.05,说明经过一阶差分后的序列已经平稳,所以d取1。按照相同方法可得,二氧化碳时间序列d取0;温度时间序列d取0。
对一阶差分后的氨气浓度序列进行白噪声检验,得到结果为5.65×10-22,远远小于0.05,说明d=1时的序列是非白噪声,d=1通过检验,使用AIC准则多次试验得到ARIMA(5,1,2)的AIC最小,为2 533.82。按照相同方法可得二氧化碳的ARIMA模型pdq取(9,0,5)的时候AIC最小,为16 563.03;温度的ARIMA模型pdq取(8,0,2)的时候AIC最小,为−477.79。
ARIMA预测后将残差输入GRU模型,初始GRU神经网络激活函数设置为tanh,用于循环时间步的激活函数设置为sigmoid,优化器采用Ad⁃am优化器,损失函数采用均方误差,GRU隐含层为3,前2层隐藏神经元个数设置为128,第3层为64,迭代次数设置为150,batch_size设置为128。
为了得到最优参数,需要对GRU模型的学习率和时间窗口这2个超参数进行优化和仿真,对于氨气浓度、二氧化碳浓度和温度这3种不同环境因子,超参数分别单独进行模拟和仿真,经过多次预实验发现,学习速率小于0.001或时间窗口大于10会导致模型训练速度过慢,学习速率大于0.01时模型预测精度明显下降,因此GRU模型学习速率取值集合为{0.001,0.003,0.005,0.008,0.01},时间窗口取值合集为{1,3,5,8,10}。
2.3 模型参数性能分析
2.3.1 不同学习速率
从集合{0.001,0.003,0.005,0.008,0.01}取不同的值作为GRU模型的学习速率并对模型的预测性能进行比较,预测效果如图8所示。

图8 不同学习率时GRU预测性能变化Fig.8 GRU prediction performance changes with different learning rates
从图8(a)~(c)可见,学习速率取0.005时,氨气预测的RMSE最小,为0.451 84,R2最大,为0.905 72,MAPE取值为0.024 49,仅大于学习速率取0.003时的MAPE取值0.454 80,故GRU氨气浓度预测模型学习速率设置为0.005;对于二氧化碳,学习速率从0.001提升到0.003时MAPE下降并取到最小值0.045 83,学习速率继续增加到0.01时MAPE反而上升,同时学习速率取0.003时,RMSE和R2均取到最优,分别为212.485 88和0.876 07,故GRU二氧化碳浓度预测模型学习速率设置为0.005;对于温度,学习速率取0.008时,RMSE和MAPE均取到最小值,分别为0.253 31和0.012 29,R2最大,为0.815 39,故GRU温度预测模型学习速率设置为0.008。
2.3.2 不同时间窗口
按照上文的最优学习速率对3种GRU模型分别进行设置,然后从集合{1,3,5,8,10}取不同的值作为GRU模型的时间窗口并对模型的预测性能进行比较,预测结果见图9。从图9(a)~(c)可见,时间窗口从1增加到5时,RMSE和MAPE不断下降,R2不断上升,因为此阶段随着时间窗口的增长,信息数据量增长,神经网络得到更加充分的训练,因此预测精度上升,随着时间窗口继续增加,信息变得冗余,故训练精度下降,所以氨气预测模型时间窗口设置为5,此时氨气预测的RMSE和MAPE分别为0.432 7和0.023 34,R2为0.913 79。按照同样的方法,二氧化碳时间窗口设置为10,温度时间窗口设置为5。

图9 不同时间窗口时GRU预测性能变化Fig.9 GRU prediction performance changes with different time windows
3 讨论
3.1 预测结果对比分析
用测试集的数据测试ARIMA-GRU模型,同时为验证ARIMA-GRU模型预测的性能和精度,将ARIMA模型、CNN模型和GRU模型的预测结果与混合模型的预测结果进行对比,取预测结果绘制图像,图10(a)~(c)分别为氨气、二氧化碳和温度预测结果对比。观察图10(a)~(c)可以看出,单一ARIMA预测模型对3种因素的拟合性能与预测效果均较差,预测值与实际值的误差较大,因为ARIMA不擅长复杂序列的处理。CNN模型和GRU模型的预测值变化趋势与实际值变化趋势整体上是一致,且基于GRU模型的预测方法相比于基于CNN模型的预测方法具有更好的拟合效果。虽然GRU模型预测精度高于CNN模型和ARI⁃MA模型,但是总体预测结果的误差还是偏大。ARIMA-GRU模型相比GRU模型有所提升,可以更好拟合3种环境因素,说明ARIMA的线性拟合能力可以优化GRU模型预测精度。
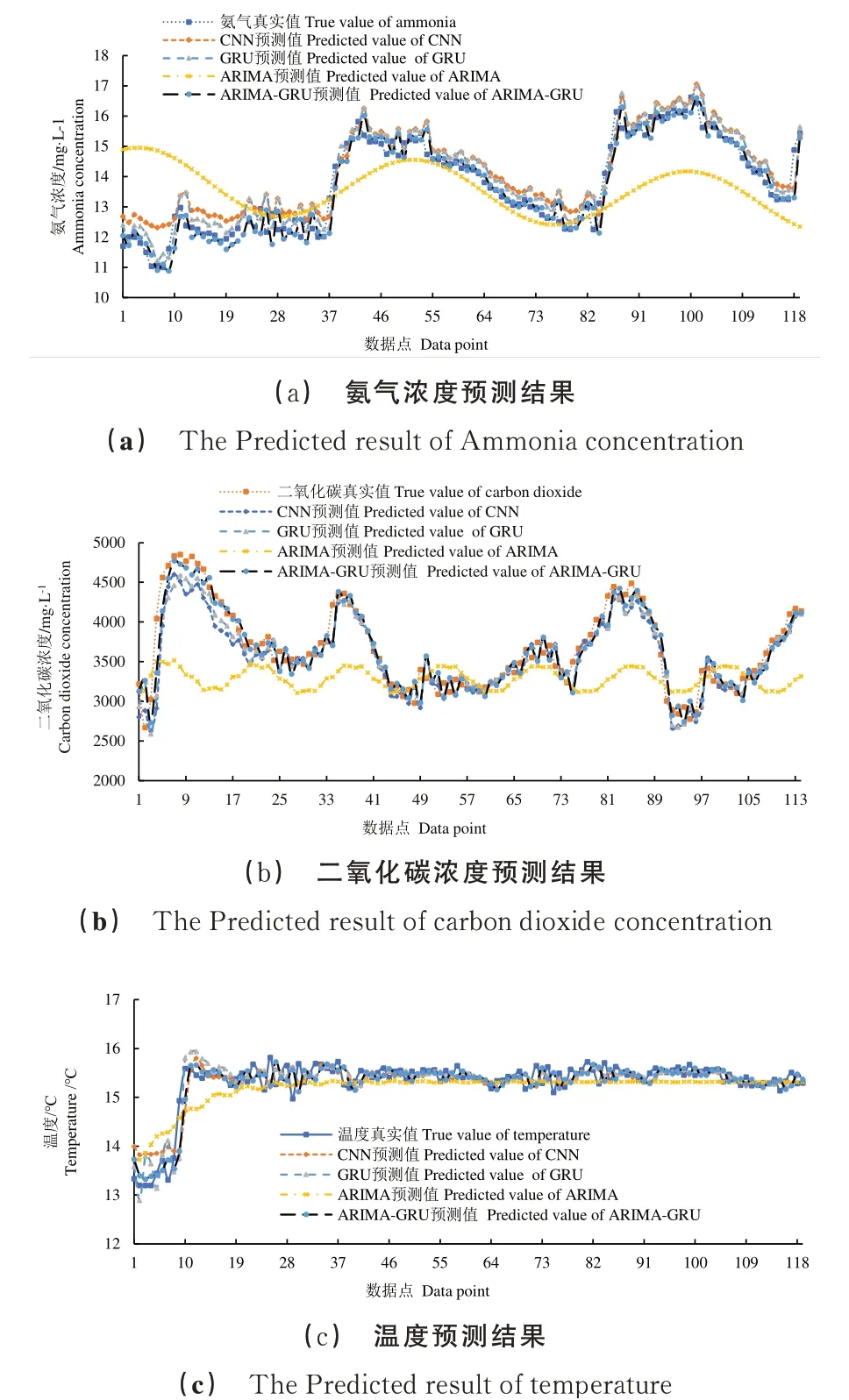
图10 3种不同环境因子预测结果对比Fig.10 Comparison of results predicted by three different environ⁃mental factors
3.2 不同模型评估结果对比分析
用不同指标对3种环境参数预测性能进行评估(表1~表3)。基于ARIMA-GRU模型环境参数预测方法的决定系数R2分别为0.913 8、0.874 8和0.819 9,模型拟合效果比较好,与基于单一GRU模型的环境参数预测方法相比,RMSE和MAPE分别平均降低了11.35%和13%,R2平均提升了3.8%;与基于单一ARIMA模型的环境参数预测方法相比,RMSE和MAPE分别平均降低56.42%和61.58%,R2平均提升661.02%。ARI⁃MA-GRU预测模型在氨气浓度预测上具有最好的预测效果,RMSE、MAPE和R2分别为0.432 7、0.023 3和0.913 8,在温度预测上具有最差的预测效果,RMSE、MAPE和R2分别为0.229 0、0.011 1和0.819 9。ARIMA-GRU对GRU在氨气浓度预测上的精度提升效果最好, RMSE和MAPE分别降低了15.78%和27.41%,R2提升了4.02%,对GRU在温度预测上的精度提升效果最少,RMSE和MAPE分别降低了4.74%和2.63%,R2仅仅提升了2.3%。综上所述,ARIMA模型预测效果最差,ARIMA-GRU模型预测效果最好,相比其它单一模型的预测值更接近真实值,可用于规模化养殖猪舍中环境因素预测。

表1 氨气浓度预测模型评估Table1 Evaluation of ammonia concentration prediction model

表2 二氧化碳浓度预测模型评估Table2 Evaluation of carbon dioxide concentration predic⁃tion model

表3 温度测模型评估Table 3 Evaluation of temperature prediction model
4 结论
(1)通过训练与仿真对GRU模型超参数进行优化,氨气浓度预测模型、二氧化碳浓度预测模型和温度预测模型的学习率分别设置为0.005、0.003和0.008,时间窗口分别设置为5、10和5时模型预测精度较高;
(2)GRU模型对环境因素预测的RMSE、MAPE和R2的平均值分别为70.774 3、0.028 6和0.837 5,预测效果优于单一AIRMA模型和单一CNN模型;
(3)ARIMA-GRU模型对氨气浓度、二氧化碳浓度和温度预测的决定系数R2分别为0.913 8、0.874 8和0.819 9,在氨气浓度预测上具有最好的预测效果,在温度预测上具有最差的预测效果,且对GRU氨气预测提升最大,温度预测提升最小。ARIMA-GRU模型与单一GRU环境因素预测模型和单一ARIMA环境因素预测模型的预测结果相比具有更小的误差和更高的精度,可为猪舍环境控制提供一定的科学依据。

