下击暴流作用下菱形马鞍面屋盖风压特性

褚云朋，孙鑫晖，李 明，姚 勇，黄汉杰

(1. 西南科技大学土木工程与建筑学院，四川，绵阳 621010；2. 中国空气动力研究与发展中心，四川，绵阳 621010)

下击暴流发生突然，破坏力较强，是非台风地区的主要强风，实测速度达到67 m/s[1]，因其对建筑物造成巨大破坏受到广泛关注[2]。大跨结构对强风作用极其敏感，尤其是体型复杂的大跨结构，还需考虑风压分布不同对其造成的失稳破坏。现阶段学者们针对大气边界层风作用下复杂结构的风载进行了各类研究。郑肖楠等[3]对条形封闭网架煤棚的风荷载分布规律进行了试验研究，得出了各风向角作用下煤棚表面的风载规律。郭薇薇等[4]对某大跨度公、铁两用桁架斜拉桥车桥系统进行风洞测试。孙瑛等[5]针对大跨结构探究了抗风夹间距对屋面承载力的影响。而大跨结构对于类似于下击暴流的强风荷载更加敏感。

Sengupta 等[6]制作模型模拟立方体建筑物在下击暴流作用下的风载特性，并将结果与规范进行对比分析。Chay 等[7]证实建筑表面风压与普通大气边界层风下不同。Asano 等[8]制作了向上喷射的下击暴流冲击射流装置，并对立方体进行测压试验。吉柏锋等[9]以某高层建筑为原型分析表面风压分布特性，表明模型迎风面风压最大出现在中下部约1/3 处。李宏海等[10]用二维下击暴流模型对高层建筑风压进行研究，得出下击暴流作用下的建筑物体型系数大于规范参考值。Jesson 等[11]及江鹏[12]对门式刚架在下击暴流作用下进行对比，表明厂房径向位置对其表面风压影响大。席保锋[13]分别对不同高宽比的圆形和方形高层建筑表面风压进行分析，得出风剖面特性较明显。李艺等[14]利用CFD 模拟得出了风暴的移动对风暴前缘有加速作用，而对风暴后方有减速作用。Yumi等[15]用大涡模拟法描述了下击暴流产生荷载的过程。陈勇等[16]通过下击暴流试验研究了地面粗糙度对拱形屋盖风压特性影响。方智远等[17]分析得出，深宽比增大，高层建筑的层平均阻力系数有所减小。邹鑫等[18]通过试验得出扭转向层风荷载谱沿高度有显著变化，汪之松等[19]在前面基础上进一步研究径向距离对低矮建筑气动力特征影响。

菱形马鞍面屋盖由于本身结构特点，其屋盖受风载影响巨大，尤其是下击暴流类的强风荷载。李清雅等[20]利用大气边界层风研究了菱形马鞍面屋盖的风载特性。孙虎跃等[21]通过研究得出马鞍面最大风吸力出现在迎风低点附近。崔碧琪等[22]分析了菱形马鞍面屋盖在下击暴流作用下的风压分布，但对比分析参数较少，考虑到菱形马鞍面造型复杂，易受强风荷载影响，仍需进一步对其受径向距离和风向角等参数的影响进行分析。在大气边界层风作用下，屋盖分压随建筑物高度增加而增加，而由于下击暴流风场与大气边界层风不同，故在其作用下，屋盖在某一特定高度作用下产生的破坏最大；在下击暴流作用下不同的径向位置的风场变化不同也会导致屋盖风压不同。

通过冲击射流装置模拟下击暴流，设计制作了菱形马鞍面大跨屋盖结构缩尺模型，进行刚性模型表面风压试验研究，分析不同径向距离和风向角对下击暴流作用下菱形马鞍面大跨结构屋盖表面风压分布的影响，为抗风设计提供基础数据。

1 试验研究

1.1 试验装置

试验采用中国空气动力研究与发展中心的冲击射流装置(如图1 所示)。该装置气流喷口最大风速为27.3 m/s，喷口高度可在0.6 m～2 m 范围内进行调节，底板采用光滑的刚性模板。根据试验方案设置喷口直径Djet=600 mm、喷口到刚性模板的距离为H=2Djet，喷口射流风速为Vjet=10 m/s。

图1 冲击射流装置Fig. 1 Impact jet device

1.2 模型设计

试验主要测量模型表面的风压分布情况，不涉及结构的动力响应，故设计制作刚性模型(如图2 所示)。模型的马鞍面曲率p为1/225，菱形马鞍面边长取110 mm，高点高度45 mm，低点高度22.5 mm，建筑物矢跨比为1/6。模型缩尺比1∶1000，本次测压试验选用的扫描阀精度为0.2% FS。

图2 建筑物模型Fig. 2 Building model

由于菱形马鞍面的几何模型复杂，模型在不同位置产生风压分布规律性较差，为更好得出屋盖上每个区域风压分布情况，如图3 所示，模型上测压点采用间隔10 mm 均匀加密方式布置。在模型设计测点处取孔并固定测压管，保持气密性，测压管另一端连接扫描阀。本模型共设置121 个测压点，布置如图3 所示(测点1 处于模型高点区域)。

图3 测点布置Fig. 3 Measuring points arrangement

1.3 工况设计

Chen 等[23]指出下击暴流冲击到地面后径向扩散，径向风速最大值出现在距离喷口中心1.00Djet附近，为探讨径向距离的影响，试验设计模型中心到喷口中心距离取0.00Djet、0.75Djet、1.00Djet、1.25Djet、1.50Djet、1.75Djet、2.00Djet。制 作 单 位为15°圆盘，将模型精确固定在圆盘上，根据划分的刻度线调整圆盘，用于改变风向角大小。其中0°风向角正对测点1，90°风向角正对测点11。工况设计见表1，图4 为建筑物模型位置示意图。

图4 不同径向距离下各工况模型位置Fig. 4 Model position under different radial distances

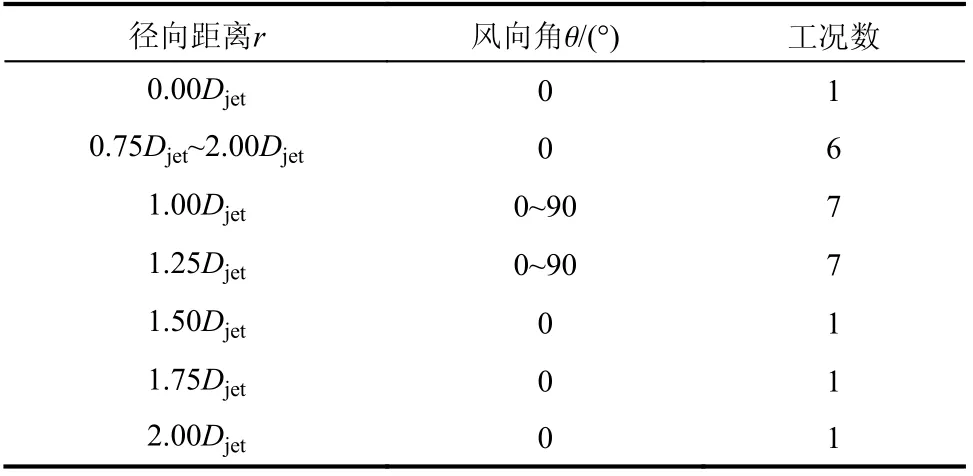
表1 试验工况设计Table 1 Design of test conditions

1.4 风场验证

试验前需对冲击射流装置产生风场进行可靠性验证。图5 反映了径向风速在不同径向距离下随高度变化趋势，与传统大气边界层风不同，下击暴流产生风场整体呈现水平风速随高度增加先迅速增大后逐渐减小，整个径向风速图呈“鼻子”状。从图5 可知：最大风速出现在r=1.00Djet时，距离地面高度约9 mm，其值约为1.0Vjet。

图5 径向风速随高度变化Fig. 5 Curve of average wind velocity with height

取r=1.00Djet下竖向风剖面与以往经典模型进行对比，由图6 可见试验结果与国外学者的研究所得结果较一致。风场试验结果表明：该装置模拟的下击暴流具有一定可靠性。

图6 下击暴流风场竖向剖面对比Fig. 6 Vertical profile comparison of downburst wind field

2 结果分析

下击暴流作用下测点表面风压系数可用下式计算得出：

式中：Cp为屋盖某点平均风压系数；P为模型表面某点参考平均风压；ρ 为空气密度，取值为1.195 kg/m3；v为参考点平均风速，取设置的冲击射流速度v=10 m/s。

根据式(1)，计算出所有测点平均风压系数。图7 是不同径向距离下平均风压系数的变化趋势，r=0.00Djet时，模型在冲击装置正下方，屋面整体呈现正压分布。r=0.75Djet时屋面所受正压开始减小。随径向距离继续增大，屋盖整体变为负压分布。r=1.25Djet时，在41 号测点出现最大平均风压，该点平均风压系数为2.44。r>1.25Djet时平均风压最大值开始迅速减小，而整体平均风压开始逐渐趋于稳定。

图7 不同径向距离下屋面平均风压系数变化Fig. 7 Average wind pressure coefficient of roof under different radial distances

根据文献[23]，下击暴流撞击地面，在1.00Djet附近得到充分扩散，出现风速极值，故针对风向角的研究，选取了r=1.00Djet和r=1.25Djet两种工况进行对比分析。如图8 所示，屋盖的整体平均风压随着风向角的增大而增大，到60°以后增长缓慢基本趋于水平。由于模型摆放距离是根据模型的中点到冲击射流出口中心位置确定，r=1.25Djet时，模型檐口贴近气流开始充分扩散的地方，故r=1.00Djet时的整体平均负风压小于r=1.25Djet。

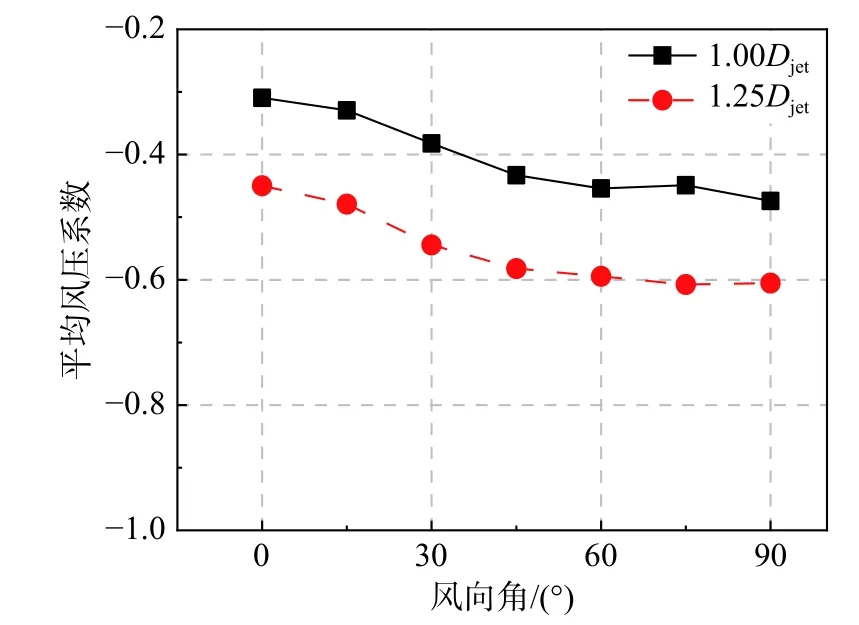
图8 不同风向角下屋面整体平均风压系数变化Fig. 8 Average wind pressure coefficient of roof under different wind direction angles

3 影响因素分析

菱形马鞍面为双曲面，其形态复杂，受强风影响时屋盖上风荷载分布不均，我国现有规范中主要针对规则屋盖进行结构设计，为更好研究菱形马鞍面屋盖风压分布，据文献[24]对该屋面分区处理。考虑压力分布状况，将屋盖表现分为角区(A1、B1、C1、D1)、边区(A2、B2、C2、D2)和中区(A3、B3、C3、D3)12 个区域。部分测点处于分区分割线上，此类测点上的风压数据由分割线两边区域共同使用，其计算从属面积与其他测点相同。θ=0°时来流方向在区域A1的左侧。其中A1和C1区分别为菱形马鞍面的两个高点区域(图9)。

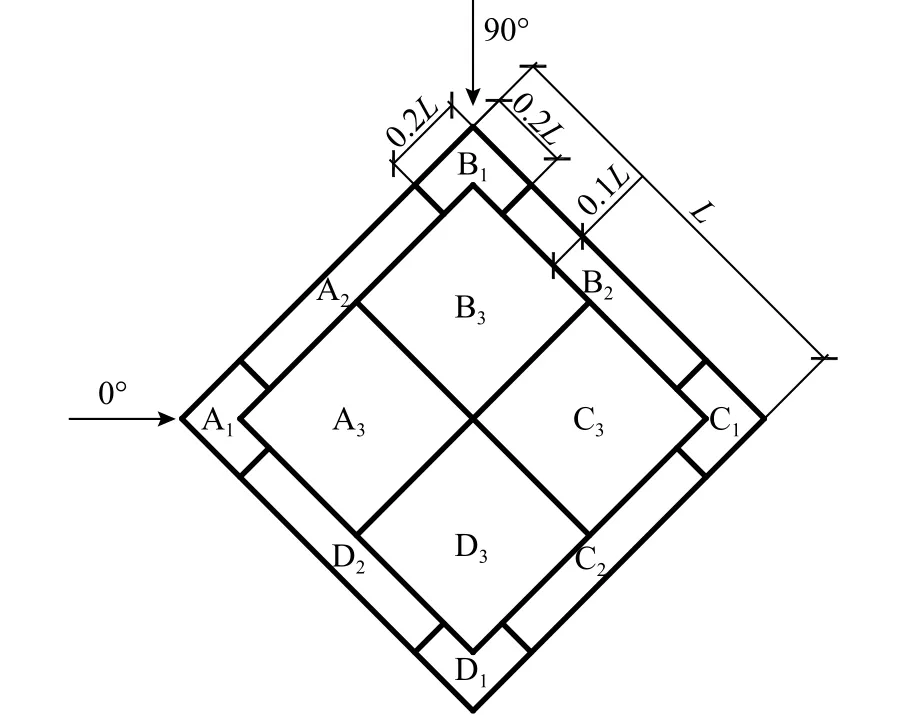
图9 菱形马鞍面分区Fig. 9 Partition on the diamond saddle

3.1 径向距离对屋盖风压影响

建筑物在下击暴流正下方和有一定径向距离时屋盖受到作用不同，以及不同径向距离下的地面扩散的气流发展状况不同，因此为探究不同径向距离下屋盖表面风压的分布特性，本次试验在设置建筑物都为0°风向角前提下，改变径向距离分别为0.00Djet、0.75Djet、1.00Djet、1.25Djet、1.50Djet、1.75Djet和2.00Djet设置相应工况。

如表2 所示，r=0.00Djet时，各分区平均风压系数较为接近。由于模型表面并不光滑，会产生部分能量的耗散，导致每个分区平均风压系数都略小于1；另外喷口和模型中心点的位置有一定误差，故各分区平均风压分布云图无法完美地沿高低点的各自连线成对称分布。

表2 0.00Djet 下各分区平均风压系数Table 2 Average wind pressure coefficient of each zone under 0.00Djet

不同径向距离下屋盖表面风压分布如图10 所示。1)r=0.00Djet时，建筑物在冲击射流的正下方，由于建筑物模型表面并不光滑，且建筑物位置有细微的偏差，故屋盖表面风压并不对称。2)r=0.75Djet时，射流冲击尚未完全扩散，部分气流竖向冲击屋盖前半部分，故屋盖整体以正压为主。3)r≥1.00Djet时，A1区是分区平均风压系数最大区域，是由于选取工况都是风向角为0°情况，A1区处于迎风面高点区域。气流撞击模型檐口，气流被分离。上层空气向下流动，下层空气向上流动，在屋顶迎风面两侧汇合，在屋檐局部区域形成负压。这两种作用叠加使A1区产生最大平均风压。在向下通风方向，空气重新附着在屋顶上，因屋顶向上倾斜，故屋顶上正压力较小。4)在r≥1.00Djet时，随径向距离增加，大部分分区平均风压系数(绝对值)都呈先增大后减小趋势，在r=1.25Djet时出现最大平均风压。5)平均风压系数沿高点连线方向的变化梯度在r=1.00Djet时最大；沿高点连线的平均风压变化梯度随径向距离增加逐渐减小。6)r≥1.00Djet时，正压区集中体现在C1区，中间正压区的区域大小随径向距离增加而减小。正压区的平均风压系数普遍都小于0.2，可见r≥1.00Djet时，正风压对此类屋盖表面风压影响很小。

图10 不同径向距离下屋盖表面风压分布Fig. 10 Wind pressure distribution on the roof under different radial distances

图11 为不同径向距离下每个分区平均风压变化趋势，对于A1、A2、D2三个迎风面区域，由于径向距离对该区域锥形涡影响较大，导致该三个区域的风压系数变化趋势很明显，在到达1.25Djet产生最大平均风压之后，风压系数稳定减小。分析变化趋势最大的A1区：1)r=1.25Djet时，A1区的平均风压系数是r=1.00Djet时的1.5 倍；2)r>1.25Djet时，平均风压系数减小速度近30%。r≥1.00Djet时，随着径向距离增大，除了迎风面的三个区域，其他区域的风压系数基本趋于稳定，说明在r≥1.00Djet时，径向距离对此区域影响小。

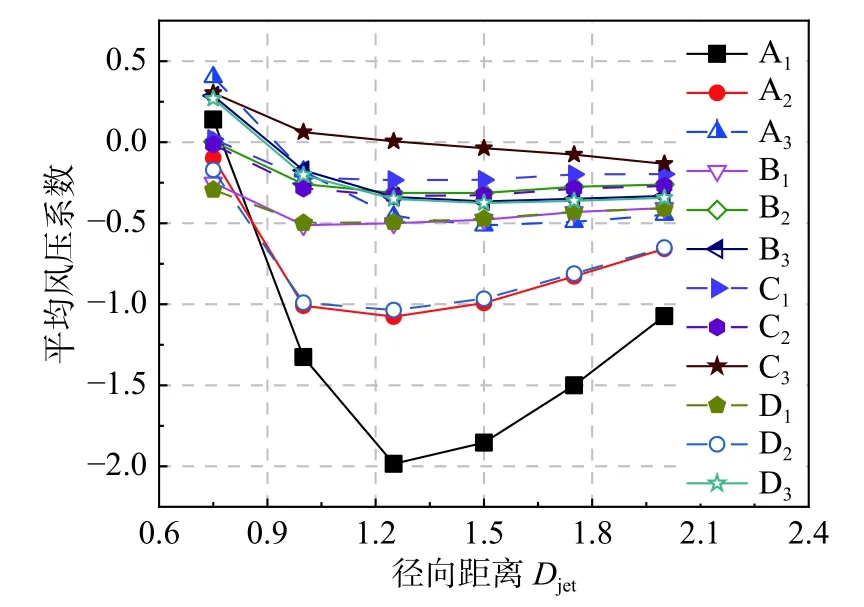
图11 不同径向距离下各分区平均风压系数Fig. 11 The average wind pressure coefficient of all zones under different radial distances

3.2 风向角对屋盖风压系数的影响

为研究风向角对模型表面风压分布影响，试验选取了径向距离为1.00Djet和1.25Djet时、风向角为0°～90°(每15°递增)的工况进行研究。

3.2.1 不同风向角下菱形马鞍面屋面风压变化

如图12 所示：1) 风向角为0°时，迎风面的A1、A2和D2区平均风压云图呈现向两边分开的花瓣状，气流在檐口撞击分离出的锥形涡对这三个分区产生影响较大，形成的旋涡产生风吸力，迎风高点A1区分区平均风压系数达到-1.99；2) 气流沿着建筑物高点连线流向背风面，风吸力减弱，气流在C3区域附近再附着，局部产生正压。再附着气流撞击屋面后，再次分离，导致C1区部分产生负压。

图12 不同风向角下屋盖表面风压分布(r=1.25Djet)Fig. 12 Wind pressure distribution on the roof under different wind directions (r=1.25Djet)

随风向角继续增大屋面表面风压变化情况：1) 风向角增大到15°和30°时，A2区开始形成负压，正压区转向D3区；2)风向角增大到45°时，模型侧面正对来流方向，气流撞击侧面产生竖向的分离泡，在迎风低点的B1区域产生最大平均风压，该分区风压系数为-1.07，θ=60°时最大分区风压系数也出现在B1区域，最大值为-1.16；3) θ=75°时，最大负风压在迎风面A2区，是由于迎风低点趋于中心线，气流在侧面区域开始加速；4)风向角为90°时，菱形马鞍面低点正对来流方向，由于分离气流从马鞍面低点区域向上凸方向流动时会产生加速效应，导致两侧开始产生较大负压，沿两侧区域平均风压呈先增大后减小趋势，到两侧高点前出现衰弱，负压值开始下降。

3.2.2 不同风向角下屋盖各分区平均风压变化

分析各分区风压能更好找到屋面最不利位置，分析不同风向角下分区风压系数变化，可看出每个区域最不利风向角及所有工况下最不利区域。图13～图15 分别列出各分区上风压系数变化，对角区、边区和中区分别进行分析。

图13 不同风向角下角区平均风压系数Fig. 13 The average wind pressure coefficient of the lower corner area at different wind direction angles

图15 不同风向角下中区平均风压系数Fig. 15 Average wind pressure coefficient in the middle zone under different wind direction angles

角区分区风压系数变化最大，如图13：1) A1在θ=0°时处于迎风面，风吸力最大，产生的负风压最大。A1区的风压系数随着风向角的增大而减小。在1.25Djet时，0°角建筑物檐口产生严重的流动分离，故风向角在0°～30°时，A1区风压变化速度很快。2) B1区是低点连线上的角区，在45°左右时风压最大。分区风压系数随着风向角的增大呈现先增大后减小的趋势。60°时，气流撞击屋盖侧面，产生风向较为复杂，1.25Djet时的B1区风压继续增加。3)风向角为0°～60°时，C1区一直处于整个模型后方，受再附着气流后撞击产生小旋涡影响，处于较小负风压状态。75°和90°时，气流在模型侧面从低点到高点向上冲击，C1区负风压越来越大。4) D1区最大平均风压系数在-0.5 附近，出现在θ=0°工况下。随风向角增大D1区距离变大，分离气流产生风吸力作用减小，平均风压系数减小。

边区分区风压系数变化见图14：1) A2区在75°时风压最大，此时气流从低点分离后加速经过了A2区。在不同径向距离下，地面风速不同，在75°时气流撞击屋盖产生的涡有较大差异，此时两种径向距离下A2区差异较大。2) B2区最大风压出现在90°，此时气流从B1区正面冲击，在顶点气流向两边分离，加上90°时气流从低点向上，到顶点前有加速作用。3) C2区最大风压出现在90°，但与B2区不同，气流翻过高点在C2区已经减速，故C2区的风压略小于B2区。4) D2区最大平均风压出现在θ=0°时，分区平均风压系数近1.1，随风向角增加，D2区平均风压系数减小。

图14 不同风向角下边区平均风压系数Fig. 14 The average wind pressure coefficient of the lower edge area under different wind direction angles

中区分区风压系数变化趋势见图15：1) A3位于菱形马鞍面的中间区域，0°的时候A3区处于A1后方，由于气流分离作用迅速减小，导致该区域负风压较小。风向角增大，高点连线偏移，迎风面高度逐渐降低，A3区逐渐暴露在迎风口，在45°左右时负风压达到最大，风向角继续增加，A3区到迎风口距离变大，负风压降低。2) B3区负风压呈现先增大后减小的趋势，最大风压系数达-0.8。3) C3区域在风向角变化下，随与迎风面距离增大，负风压逐渐增大。4) 在风向角为30°时，气流撞击模型侧面，气流分离后在该区域再附着，故在D3区产生较小正压。

由于菱形马鞍面原点中心对称，所以选取的0°～90°可以推出各区域在所有风向角下的风压分布状况。总体来说，角区在某些风向角下都会出现较大的负风压，分区最大平均风压系数超过-1.9；边区负风压虽然略小于角区，但是部分分区平均风压系数超过-1.2；中区产生的风压最小，平均风压系数都不超过-1.0，相对安全。

4 分区风载体型系数

下击暴流在结构周围产生的风场与传统大气边界层风不同，且菱形马鞍面屋盖形状特殊，故需通过风洞试验数据对屋盖风载体型系数进行相应计算。根据文献[24]方法，将风洞试验常用公式(式(2))和规范[25]中的公式(式(3))相结合得出式(4)。

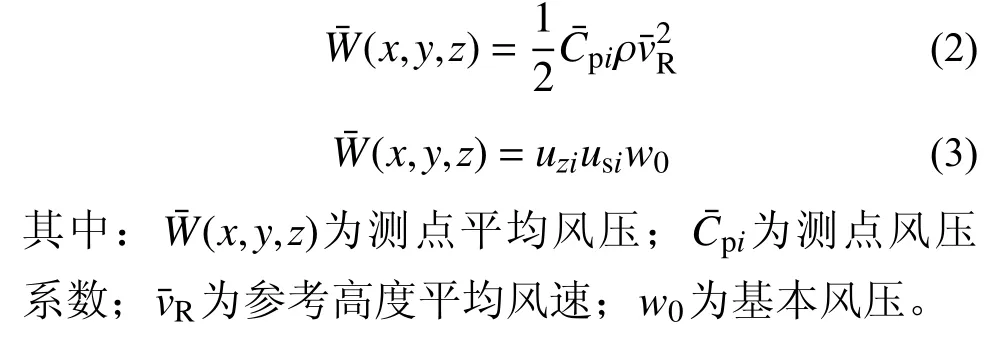
其中：usi为某一测点的风载体型系数；cz取值根据文献[25]；zR为参考高度(取模型高度)；z为测点高度； α为地面粗糙度。

分区的风载体型系数等于该区域所有测点的风载体型系数乘测点从属面积，且进行加权平均[25]，见下式：

取r=1.25Djet时的数据进行计算，表3 为在不同风向角下各分区的风载体型系数，由式(5)计算得出。可看出，整个菱形马鞍面基本以风吸力为主，角区风载体型系数更大，最大风载体型系数是处于高点的A1区；由于气流在迎风檐口处分离复杂，各分区差距大。

表3 屋面各分区风载体型系数Table 3 Wind load shape coefficients of roof areas

5 结论

本文利用冲击射流对下击暴流进行模拟，针对菱形马鞍面研究其屋盖风压特性，并研究径向距离和风向角对屋盖各区域风压的影响，得出结论如下：

(1)r=0Djet时屋面受正压作用，由于能量的耗散，所有测点的风压系数都在0.95 左右。当r>0.75Djet时，风吸力主要是由气流分离产生的，气流撞击屋盖前缘产生了旋涡脱落，屋盖表面以负风压为主，故其屋盖进行结构设计时需着重考虑屋盖掀起破坏。

(2)风向角对屋盖风压的影响很大，下击暴流冲击不同的风向角下建筑物会产生不同的气流分离情况，屋盖高点处于迎风面时其气流分离最为严重。试验中风向角为0°时产生最大平均负风压出现在41 号测点，其最大平均负风压系数为-2.44。所有分区最大平均负风压是在此工况下的A1区，其系数为-1.99。故结构设计时应考虑风向角对菱形马鞍面屋盖风载影响及屋盖局部加强。

(3)屋面整体平均风压系数(绝对值)随风向角增大而增大。菱形马鞍面中间区域在各工况下平均风压系数较小，屋面最不利位置在高点连线的两个角区，当来流向正对高点连线(风向角为0°)，A1 区会产生最大平均风压。

(4)相比较而言，角区和边区的风载体型系数更大，最大达到-2.75，建议进行结构设计时对菱形马鞍面四周区域进行局部加强。